李 娜，郑少智

（暨南大学 经济学院，广州 510632）

0 引言

股票市场作为市场经济的一个重要组成部分，对国民经济的发展有着非常重大的作用，股票市场的繁荣和稳定是国民经济的“晴雨表”，所以，有许多的经济学家和实际工作者对股票市场进行了深入地研究，结果发现，对于常用的股票模型，比如：AR模型、ARCH模型以及ARIMA模型等并不能很好地刻画出股票的市场行为，但随着非线性时间序列分析的近二十年的发展，其在经济、金融等领域有着广泛的应用前景，这些非线性模型能够更好地模拟实际经济和金融中的数据。对于平滑转换自回归（STAR）模型，常用的两种模型有：逻辑斯蒂平滑自回归（LSTAR）模型和指数平滑自回归（ESTAR）模型，这两种模型分别是以逻辑斯蒂函数和指数函数作为平滑函数来建立STAR模型，本文采用是高斯核函数作为平滑函数来建立STAR模型，并将该模型用于股票市场特性的研究中，通过实证研究结果表明，该模型能够很好地刻画出股票的市场行为。

1 STAR模型的建立

1.1 模型的描述

STAR模型由Granger和Teräsvirta于1993年提出以来，目前已经形成了一套比较成熟的建模程序，包括平滑转换自回归模型（STAR）的设定与估计以及如何确定平滑函数等。一个二制度的STAR模型的一般表达式为：

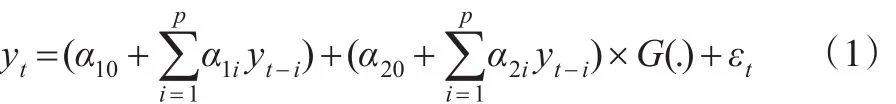
其中，yt是研究的时间序列，α10、α20是常数，p是所研究时间序列的滞后阶数，εt是独立同分布的随机变量，G(.)是一个连续的平滑函数，取值范围为[0,1]，它决定了两个制度之间相互转换的方式，当 G(.)=0时，yt是一个AR(P)过程；当 G(.)=1时，yt是一个两机制混合的AR(P)过程；当0＜G(.)＜1时，yt在两机制之间平滑的转换，而转换的方式由G(.)的具体函数形式决定。G(.)可以是连续的奇函数或偶函数，例如G(.)可以是满足G(-∞)=0与G(+∞)=1的单调递增的奇函数，也可以是满足G(±∞)=0 与G(0)=1的偶函数，比如正态分布 N(μ'σ2)的累积分布函数和正态分布N(μ'σ2)的密度函数都可以作为平滑函数来建立平滑转换自回归模型。

对于平滑函数G(.)，目前常用的两种平滑函数包括逻辑斯蒂函数和指数函数，其中，逻辑斯蒂函数的具体表达式如下：

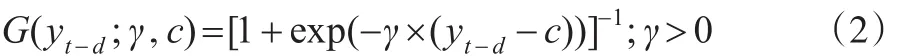
其中，yt-d是门限变量，d是延迟参数，c是两个机制之间的门限值，若平滑函数 G(.)设定为这种逻辑斯蒂函数形式，则式（1）被称为逻辑斯蒂平滑自回归模型，即LSTAR模型。

随着 yt-d的增加，逻辑斯蒂函数 G(yt-d;γ'c)从0到1单调递增，转换参数γ的大小决定了该函数的平滑性，即决定了机制转换的速度，假如转换参数γ的值很大，那么门限变量yt-d相对于门限值c的很小的变化都会导致机制间的剧烈转换。当γ→+∞时，函数G(yt-d;γ'c)从0到1的变化几乎是瞬时的，此时有G(yt-d;γ'c)=I(yt-d＞c)，在这种情况下，LSTAR模型变为SETAR模型；当γ→0时，G(yt-d;γ'c)=0.5，此时的LSTAR模型变为线性AR模型。

另一种平滑函数是指数函数，其具体表达式如下：

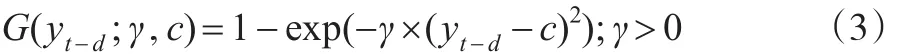
其中，yt-d是门限变量，d是延迟参数，c是门限值，若平滑函数G(.)设定为这种指数函数形式，则式（1）被称为指数平滑自回归模型，即ESTAR模型。

随着 yt-d趋于c值，函数G(yt-d;γ'c)趋于0；随着yt-d远离c值，G(yt-d;γ'c)趋于1。经过研究表明，ESTAR模型比较适合时间序列出现拐点的情况。当γ→+∞时，G(yt-d;γ'c)=1，当γ→0时，G(yt-d;γ'c)=0，所以，不论是γ→+∞还是γ→0，ESTAR模型都退化为线性AR模型。

1.2 STAR模型的估计

在估计STAR模型之前，首先需要对时间序列的平稳性进行检验，因为在一般情况下，未经处理的金融数据都是非平稳的，如果直接对非平稳的时间序列进行回归分析，那么就会造成伪回归问题，所以，在进行模型的估计之前首先需要对数据进行平稳性检验，如果数据非平稳，那么就要对数据进行处理使其平稳，比如进行一阶差分，或者用对数收益率数据等。

STAR模型的估计由以下三个步骤组成。

（1）确定线性AR模型。可以根据Ljung-Box统计量来检验残差的自相关性，在残差序列不存在自相关的条件下，可以根据Akaike information criterion(AIC)来选择线性AR模型的最大滞后阶数P。

（2）依据延迟参数d的不同取值进行线性检验，拒绝线性检验的同时，也确定d的取值。一般情况下，d的取值是1≤d≤p的正整数，也可以根据实际情况适当的调整d的取值范围。当d取不同的值时，分别进行线性性检验，H0：线性AR模型成立；H1：STAR模型成立。因为非线性模型中有线性模型不存在的参数，所以不能直接进行检验，Luukkonen等（1988）提出，可以将平滑函数G(.)在γ=0时用三阶泰勒公式展开，由此得出以下回归模型：

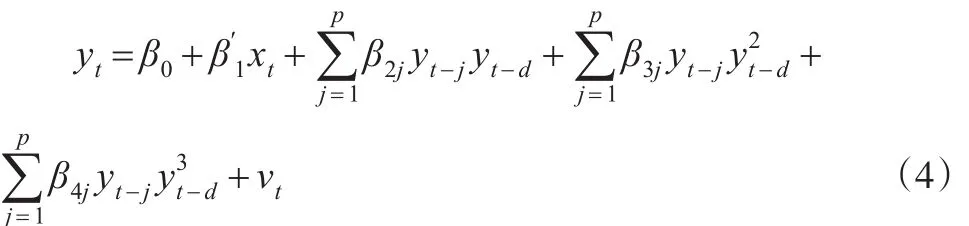
其中是误差项。

原假设为：

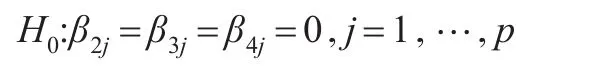
对式（4）进行LM检验，当所用数据为小样本时，LM统计量服从F分布，LM统计量在大样本情况下渐进服从卡方分布，计算出LM统计量的值和P值，如果有多个d值相对应的上式拒绝线性原假设，那么就应选择最小的P值所对应的d的取值。

（3）利用嵌套假设的序贯检验对LSTAR模型和ESTAR模型进行选择。d值确定以后，需要检验的序贯假设是：

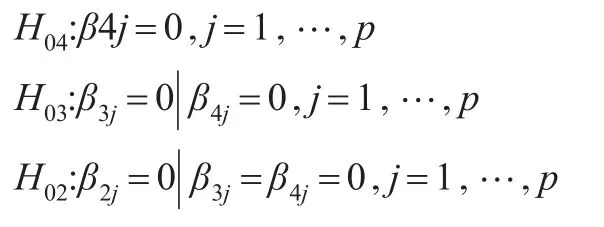
若拒绝H04，则选择LSTAR模型；若接受H04而拒绝H03，则选择ESTAR模型；若接受H04和H03而拒绝H02，则选择LSTAR模型。

Granger和Teräsvirta（1993），Teräsvirta（1994）提出，严格按照以上序贯检验的步骤对LSTAR模型和ESTAR模型进行选择也有可能得出错误的结论，所以他们认为可以计算出上述三个假设的所有LM检验的P值，若H03的P值最小，那么就选择ESTAR模型；否则，就应选择LSTAR模型。

选择好具体的模型之后，再对模型进行非线性最小二乘估计，求出模型参数的估计值，并对残差进行Ljung-Box自相关性检验和ARCH异方差性的检验，目的在于检验所建立的模型是否充分适当。

2 基于非参数平滑的STAR模型

根据前文所述，平滑转换自回归（STAR）模型在制度间的转换是连续平滑的，转换方式取决于所选取的平滑函数，常用的两种平滑函数为逻辑斯蒂函数和指数函数。随着非参数平滑技术的逐渐成熟，其在很多领域都有广泛的应用，所以本文用基于非参数平滑的方法去建立STAR模型，即选择核函数为平滑函数来建立STAR模型，然后再对模型进行估计。其具体的表达式为：

其中，Kh(.)=K(./h)/h，h为非参数平滑的带宽或者叫平滑参数，yt-d为门限变量，c为门限值。核密度函数K(.)在(-∞'+∞)上满足以下条件：

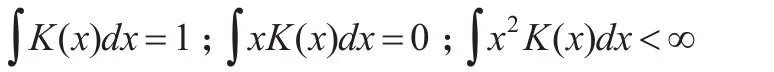
其中，带宽h也需满足：

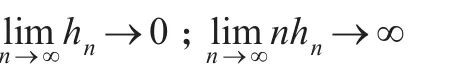
常用的核函数包括高斯核函数和对称贝塔(Beta)族：

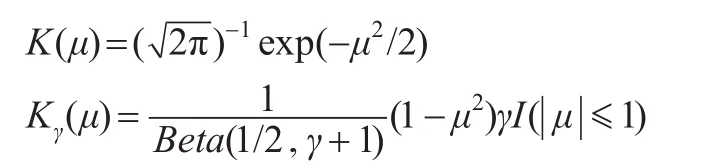
当γ=0'1'2和3时，分别对应于均匀核函数、Epanechnikov核函数、双权（Biweight）核函数和三权（Triangle）核函数。

在非参数平滑技术中，一个核平滑性能的优劣，取决于核函数和平滑参数h的选取。范剑青和姚琦伟在其所著的《非线性时间序列》一书中指出，无论是从经验的角度还是从理论的角度，核函数的选择并不是太重要，只要所选的核函数是对称的和单峰的，并且当平滑参数h的选择是最优时，核函数的选择对非参数平滑的优劣性几乎没有影响。平滑参数h是控制平滑精度的主要参数，太大的h会使得平滑过度，太小的h会导致平滑不足，所以选择一个最优的平滑参数h至关重要。

根据研究表明，对最优平滑参数的选取，可以用最小化MISE（mean integrated square error）的方法，得出渐近最优平滑参数，下面给出正态参考带宽选择：

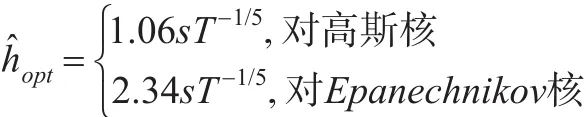
其中s是样本标准差，T是样本数量。正态参考带宽选择在数据近似为高斯分布时，它是一个很好的平滑参数的选取方法，而且根据许多的实际应用的结果表明，这种选择方法是合理的，然而，正态参考带宽选择只是一个简单的经验方法，当数据的真实分布是非对称的或者是多峰时，它就有可能导致平滑过渡，在这种情况下就需要主观地调整h，或者用更精细的方法来选择最优的平滑参数。

另外一种常见的最优平滑参数的选择方法是交叉验证法（cross-validation,简记为CV），其基本思想是，去掉第i个观测值，得到m(x)的具有平滑参数h的缺一估计：

使用上述估计量，得出缺一交叉验证得分：

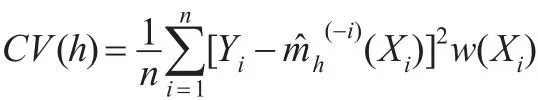
其中w(x)为非负的权因子函数，在一维的情况下可取w(x)=I( ||x-0.5≤0.4)

自动最优平滑参数定义如下：

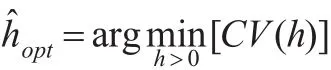
3 实证分析

3.1 数据与平稳性检验

本文选取了中航地产从2013年7月10日至2014年9月5日的共286个日收盘价数据进行实证分析，数据来源于Wind资讯。下面给出日收盘价数据的时间序列图，见图1。

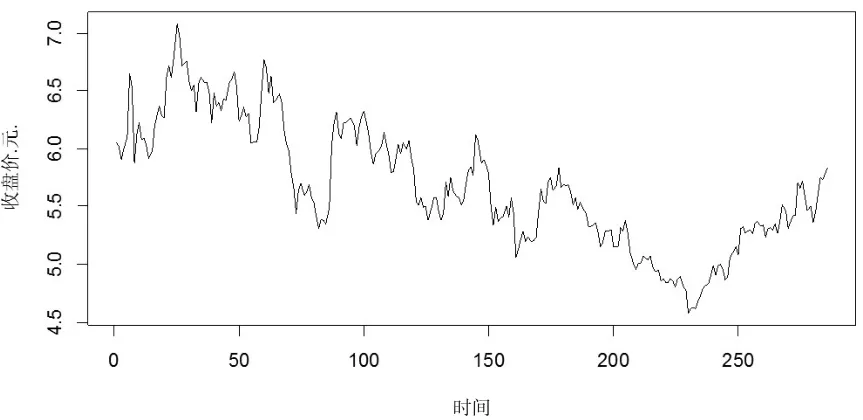
图1 中航地产日收盘价数据

根据前文所述，在建立模型之前需要对数据进行平稳性检验，所以本文用增广的迪基-富勒检验来检测该时间序列的平稳性，其检验结果如表1所示：

表1 变量的平稳性检验结果

检验结果由R软件编程计算得出，在该检验中，原假设H0为时间序列非平稳，备择假设H1为平稳，根据表1，计算的P值为0.4142，所以在5%水平下不能拒绝原假设，说明中航地产的日收盘价数据是非平稳的，为进一步分析，必须要对数据进行处理使其通过平稳性检验，所以本文选择用对数收益率数据来进行分析，图2为中航地产的对数收益率数据的时间序列图。

图2 中航地产日对数收益率数据

再对日对数收益率数据进行单位根检验，检验结果如表2所示：

表2 变量的平稳性检验结果

根据表2的检验结果，P值为0.01，所以在5%的水平下拒绝原假设，即该对数收益率数据具有整体平稳性。

3.2 线性性检验、STAR模型的设定与估计

本文实证分析部分的主要步骤为：（1）确定线性AR模型的最大滞后阶数P；（2）进行线性性检验并确定延迟参数d；（3）对模型参数进行估计；（4）对模型残差进行检验。

根据Granger和Teräsvirta（1993）的建议，可以根据偏自相关图和AIC准则或SC准则来确定最大滞后值P，由此，本文确定最大滞后阶数P为5。

接下来进行线性性检验并确定延迟参数d的值，d的取值范围为1≤d≤5的正整数，所以对每个d值，分别进行线性检测，并计算出相应的P值，结果如表3所示：

表3 线性性检验结果

根据表3的检验结果，在5%的水平下，当d取值为2和4时拒绝线性性假设，在这种情况下应取最小的P值所对应的d的取值，所以，延迟参数d=2。

在用非参数平滑建立STAR模型时，需要对核函数和平滑参数进行选择，本文选用高斯核函数作为平滑函数，并用交叉验证法（CV）计算出平滑参数h，再对STAR模型进行非线性最小二乘估计，得出STAR模型为：

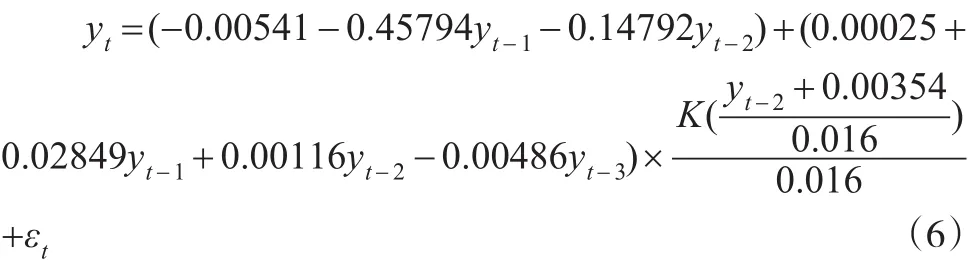
其中，门限值为-0.00354，平滑参数h为0.016，核函数K(.)为高斯核函数，即：

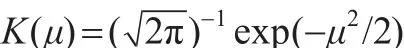
在平滑函数中位置参数d=2，说明制度转换的发生取决于自身滞后的第二期，门限值为-0.00354，表明对数收益率在-0.00354时正处于下降与上升的中间状态。

接下来需要对拟合的模型进行诊断检验，本文选择对模型残差分别进行Ljung-Box自相关性检验和ARCH异方差性的检验，若检验结果表明模型残差不存在自相关性也不存在异方差性，则说明拟合的模型是充分适当的，检验结果如表4所示：

表4 模型诊断检验结果

由表4的检验结果可知，在5%的显著水平下，Ljung-Box检验和ARCH检验都能通过，模型残差不存在自相关，也不存在异方差，表明上述模型能很好地刻画出股票的市场行为。

接下来将该模型与线性AR模型、LSTAR模型和ESTAR模型进行一个简单的对比，分别对各个模型拟合的残差进行检验，检验结果如表5所示：

表5 模型残差检验结果

表5为上述三个模型残差的自相关性和异方差性检验的P值，在5%的显著水平下，AR模型的残差无法通过滞后六期的异方差性检验，其他的检验都能通过，但与表4结果相比，AR模型、LSTAR模型和ESTAR模型的残差检验结果都不如基于非参数平滑的STAR模型显著，也就是说，以核函数为平滑函数的拟合效果比其他模型的效果要好。并且S/SL=0.97063，S SL是非参数平滑模型回归的标准误差与AR模型回归的标准误差的比值，其值小于1，说明该模型优于线性AR模型。

时间序列模型的建立，其中一个很重要的应用就是预测，所以一个模型的优劣也可以根据预测的表现来判断，当一个模型能比其他的模型更好地预测时间序列的未来走势时，那么就说明在某些程度上该模型比其他模型更好，所以接下来本文再对模型的预测方面进行一个简单的对比。本文采用误差均方根（root-mean-square error,简记为RMSE）作为评价预测效果的标准，RMSE越小的模型则越好。

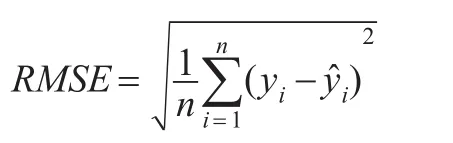
基于非参数平滑的STAR模型的RMSE值为0.0215，与表6中的其他模型的RMSE值相比，该模型的RMSE值最小，也就是说，该模型在预测方面也优于线性AR模型、LSTAR模型和ESTAR模型。

表6 模型预测评价值

根据本文的研究，无论是在样本拟合方面，还是预测方面，基于非参数平滑的STAR模型要优于其他模型，尤其是线性模型，所以可以得出股票市场具有非线性特性的结论。

4 结论

我国股票市场的经济环境复杂，使得单一传统的线性模型无法很好地刻画出股票的市场行为，本文首次用非参数平滑的方法建立STAR模型，并将该模型用于我国股票市场动态行为的研究中，通过实证研究表明股票市场的非线性特征，并证实了用高斯核函数来代替逻辑斯蒂函数和指数函数作为平滑函数来建立STAR模型是充分适当的，模型残差能够通过一系列检验，并且在该研究中，非参数平滑的STAR模型的预测效果也优于线性AR模型、LSTAR模型和ESTAR模型，由此表明，基于非参数平滑的STAR模型用于研究我国股票市场行为非常有效。

[1]Granger C W J,Teräsvirta T.Modeling Nonlinear Economic Relationships[M].Oxford:Oxford University Press,1993.

[2]Teräsvirta T.Specification,Estimation,and Evaluation of Smooth Transition Autoregressive Models[J].Journal of the American Statistical Association,1994,89(425).

[3]Tong H.Threshold Models in Nonlinear Time Series Analysis[M].New York:Springer Verlag,1983.

[4]Fan J Q,Yao Q W.Nonlinear Time Series:Nonparametric and Parametric Methods[M].Beijing:Science Press,2006.

[5]Seo M H,Linton O.A Smoothed Least Squares Estimator for Threshold Regression Models[J].Journal of Econometrics,2007,141(2).

[6]McMillan D G.Nonlinear Predictability of Stock Market Returns:Evidence From Nonparametric and Threshold Models[J].International Review of Economics and Finance,2001,10(4).

[7]Switzer L N,Picard A.Stock Market Liquidity and Economic Cycles:A Non-linear Approach[J].Economic Modelling,2016,(57).

[8]克莱夫·W.J.格兰杰，蒂莫·泰雷斯维尔塔.非线性经济的建模[M].上海:上海财经大学出版社,2006.

[9]王俊，孔令夷.非线性时间序列分析STAR模型及其在经济学中的应用[J].数量经济技术经济研究，2006,(1).

[10]薛留根.应用非参数统计[M].北京：科学出版社,2013.

[11]范剑青，姚琦伟.非线性时间序列——建模、预报及应用[M].北京:高等教育出版社,2005.

[12]王斌会.计量经济学模型及R语言应用[M].广州:暨南大学出版社,2015.

[13]谢赤，戴克维，刘潭秋.基于STAR模型的人民币实际汇率行为的描述[J].金融研究，2005,（5）.

[14]刘宇.我国股票市场的非线性研究——基于LSTAR模型[J].管理工程学报，2008，22（1）.

[15]靳晓婷，张晓峒，栾惠德.汇改后人民币汇率波动的非线性特征研究——基于门限自回归TAR模型[J].财经研究，2008,34（9）.