谢锡麟

(复旦大学 航空航天系，上海 200433)

1 追求具有一流水平的微积分教学

研习当今具有国际一流程度的微积分教程的广度与深度，以俄罗斯Zorich(卓里奇)著《数学分析》[1]等为代表的微积分教程，可归纳以下特点： ① 在讲述一元微分学基础上(第一学期)，多元微分学直接建立在有限维Euclid空间之间的向量值映照之上.Zorich的书还进一步讲述一般赋范线性空间之间映照的微分学，亦即一般赋范线性空间上的微分学.② 在讲述一元函数Riemann积分的基础上(第一学期)，多元积分学则沿用有限维Eucild空间上Lebesgue积分建立的思想和方法，甚至直接进行.③ 基于有限维Euclid空间之间微分同胚的知识，发展微分流形上的微积分[2].

上述“一流化做法”的必要性及可行性，可归纳如下：

必要性① 建立于有限维Euclid空间之间映照的微积分以及一般赋范线性空间之间映照的微分学将真正全面地展现微积分在认识自然及非自然世界中的作为；相关的系统思想及方法不仅为力学、物理学等广大基础科学和技术科学而且也为经济管理等学科提供深厚的知识基础.② 讲述一般赋范线性空间之间映照的微分学，有限维Euclid空间上Lebesgue积分建立的基本思想和方法，为进一步研习测度论以及泛函分析做了十分有益的铺垫；有限维Euclid空间中微分流形的初步理论为今后研习现代数学、力学、物理以及数理经济等较为高深的学问(相关系统思想及方法的集合)提供必要的基础.需指出，随着所研究事物的复杂度的提高，测度论以及泛函分析、微分流形等基本思想和方法是我们研究和认识复杂事物所必然需要的.

可行性① 一元微分学(面对一般实函数)建立的思想和方法，可很大程度地直接应用于有限维Euclid空间之间映照；而有限维Euclid空间之间映照的微分学建立几乎可以“一模一样”地应用于一般赋范线性空间之间映照的微分学的建立.由此，我们可以将新知识的学习过程作为“温故而知新”的过程.② 有限维Euclid空间中微分流形的初步理论实质性地基于微分同胚的相应结论，由此我们又可以实践“温故而知新”的过程.

值得指出的是，现行国内数学类专业的微积分教学一般为3学期，非数学类一般为2学期，由此教学的广度一般限于有限维Euclid空间上的微积分.经广泛实践这样的设置是合理的，并可以通过后续课程进一步提供微积分的思想与方法.微积分知识体系不仅是诸多后续数理知识的基石，而且直接为认知自然世界与非自然世界提供了系统的思想与方法.由此，研究具有一流程度的微积分教学，对创新性人才的培养具有深远的意义.

本文从方法论层面阐述数理知识体系自身研究与知识体系传播研究的若干思想与方法，并藉此实践于非数学类专业的微积分教学.

2 教学理念与方法论层面的获得——将教学理解为知识体系自身的研究与传播的研究两方面

近些年，结合笔者就相关数理知识体系的持续性研究，明晰了一种可作为世界观的“数理观点”[3]——以数理的观点认知事物的方式与方法；数理观点立足于力学、数学所属相关知识体系，并且需要各知识体系内在的融会贯通与触类旁通.我们致力于融合力学、数学相关知识体系，以期为数理方面的人才培养提供具有一流化程度的课程体系.一流化程度指课程的广度与深度可类比国内外具有一流水平的教程或专著，且学生具有一定的理论联系实际的能力.

笔者将教学理解为两个方面即“知识体系自身的研究”与“知识体系传播的研究”，如图1所示.理念上，立足于基于知识体系自身的研究以驱动知识体系传播的研究；另一方面，基于知识体系自身的研究以驱动科学与技术研究，科学与技术方面研究亦为教学提供实际背景与引导.

图1 教学的两方面构成与对应的方法论研究Fig.1 Two aspects of teaching with related methodology study

3 知识体系自身的研究

3.1 知识体系自身研究的学术基础

知识体系自身的研究区别于一般的科学与技术研究，科学与技术研究往往具有局部性的特点，致力于解决具体的一个问题或者一类问题.然而，知识体系研究致力于研究知识体系的内在发展动力(核心思想及其发展)、体系架构、应用研究，以及此知识体系与其他知识体系之间的关系；知识体系研究需要澄清所有的细节，并且需要提炼与归纳具有一般意义的思想与方法.就此，笔者获得如下认识：

知识点与知识要素以“知识点”分解“知识体系”，知识点为具有一定独立性的知识(思想与方法)的集合.每一知识点再由若干“知识要素”组成，“知识要素”可为特定的数学等式、不等式或者特定的处理思想与方法，亦称为“数学结构”，如图2(看第252页)所示.

数学通识与相似结构值得指出的是，隶属同一知识体系甚至不同知识体系的知识点可能包含相同的知识要素，称为“数学通识”，如图2所示.此外，知识体系之间亦可能存在“相似结构”，如一元微分学[4]、高维微分学[5]、一般赋范线性空间上微分学[6]具有高度相似的知识点构成，如点列极限、映照极限、映照可微性、无限小增量公式、有限增量公式、逆映照定理与隐映照定理，主要结论的分析思想与方法具有高度的统一性.

图2 数学通识/相似结构： 隶属同一知识体系或不同知识体系的知识点可能包含相同的知识要素Fig.2 Mathematical generality/similar structure： It is possible to contain the same knowledge elements by different knowledge points that can be included by one knowledge system or by different knowledge systems

数学通识与相似结构可为实现“同一知识体系之内的融会贯通”、“不同知识体系之间的触类旁通”提供一种高成效的途径.值得指出的是，数学通识亦可服务于不同课程之间的衔接.目前，笔者尝试在教学中突出“数学通识”，遵循由“结构”驱动“结论”的知识体系发展方式，此种讲授风格不仅能够有效吸引学生的注意力，而且可收获更为理想的教与学的成效.

正本清源正本清源，指深入研究知识体系的自身发展“动力”——澄清各知识点之间的关系，往往可基于共同的思想与方法来发展各个知识点.教学中表现为知识体系的发展更加符合正向思维，注重基于已有的知识发展新的知识，注重由结构驱动结论.另一方面，强调正本清源亦可以帮助学生不断回顾已学的内容，有助于获得对知识体系的全面认识.

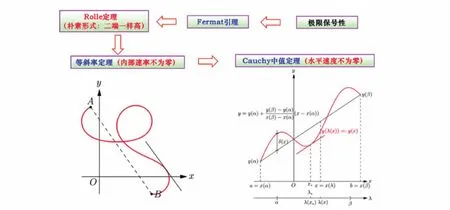
图3 正本清源的事例： 一元微分学中的中值定理Fig.3 Case of radically reform： Mean value theorem in one dimensional differential calculus

如图3所示，我们突出极限保号性决定了Fermat引理(可导的极值点其导数必为零)；由Fermat引理推出Rolle定理(叙述为闭区间上连续且内部可导的函数，如果区间内部有最值点则该点处导数为零；常见的形式是设定函数在端点上取值一致，就此决定内部有最值点)；基于Rolle定理可以获得针对一般光滑曲线与Monge曲线的中值定理.值得指出的是，多数微积分教程中阐述的Lagrange中值定理，要求运动的水平速度不为零，就此轨迹仅能为Monge曲线；只有要求运动的速率不为零，轨迹才可能为一般曲线形式.此结论的获得亦基于上述“设定函数在区间内部有最值点”的Rolle定理.

图4 格物致知的事例： 一元积分学中的积分事例Fig.4 Case of thoughtcast： An example of integral in one dimensional integral calculus

格物致知指注重将数理知识体系密切联系于认识世界的过程.例如针对微积分中对不定积分的分类，可以从力学、物理学等实际研究中寻找各种分类所对应的实际背景.如4所示，水星进动源于相对论效应，计算进动角的积分式进行简化后就是可以利用Abel变换处理的形式.教学中注重将“数学对象”联系于“物理现象”，不仅可以吸引学生的注意力，而且为认识世界提供了有效的方式.

值得指出的是，近年来笔者越来越发现，具体事物的数学机制往往可以对应于某一类数学结构，如某种形式的积分——由此，同一类积分可能成为“貌似完全无关”的不同事物的共同数学机制.教学中引入这样的背景，不仅可以使得数理教学生动活泼，而且可以帮助学生加深对事物深层机制的认识.世界的相似性，也许可以追溯为相关事物所对应的数学机制的相似性，亦即数学通识.

3.2 微积分的主要思想

3.2.1 抓住主要矛盾忽略次要矛盾

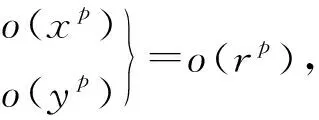
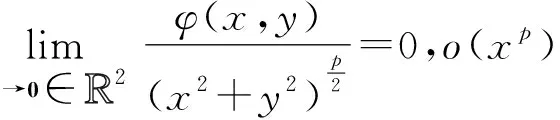
主部分离微积分中的数列极限、函数极限都具有作为充分性方法的四则运算，就此可以归纳主部分离：

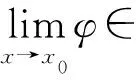
式中的极限过程可以为数列极限、函数极限、部分和极限.主部分离的思想在于先将不起主要作用的次要因素去除，以此简化所需研究的对象.在判定广义积分与级数敛散性时，主部分离亦起到重要的作用，可以表示为如下结论：

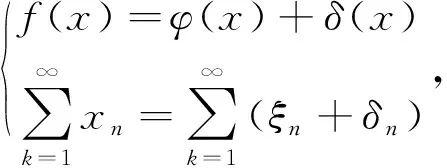
值得指出的是，广义积分与级数的敛散性的判定都基于Cauchy收敛原理(结构上一致)，而上述结论基于Cauchy收敛原理，由此广义积分与级数具有上述相似的主部分离的结论.

体积上Riemann积分的定义高维积分学中可首先在闭方块上建立Darboux和的分析理论，这一过程完全一致于闭区间上的Darboux和分析.进一步获得Lebesgue定理，亦即闭方块上多元函数Riemann可积等价于多元函数有界与几乎处处连续，以此可以定义允许集(有界且其边界为零测集)上多元函数的Riemann积分，允许集则无需几何规则.零测集的引入，可以理解为抓住主要矛盾忽略次要矛盾的一种表现.

具有零测集修正的体积分换元公式虽然高维积分学中体积分换元公式的实质基于微分同胚，但实际应用中可以对于原始的积分区域与变换后的积分区域都进行零测集修正，变换仅需要在修正后的集合之间成为微分同胚.

3.2.2 由结构驱动结论

结构指事物本质的刻画，一个事物的本质往往简洁明朗，并可归纳为若干要点；但相同的结构却可以衍生出很多问题与结论.由结构驱动结论，可以有两个方面： 1) 自身结构，指事物自身的本质刻画；2) 通识/相似结构，指不同事物具有相同的本质刻画.

有界闭集或闭区间上连续函数的性质(隶属自身结构) 一般的结论有： 有界性定理、确界可达性定理、介值定理(多元函数限定在包含于闭集的连续曲线之上)、Cantor定理(一致连续性).这些结论都可以由如下结构驱动： ① 按Weierstrass定理，有界闭集上的点列必有收敛子列；② 按闭性，收敛子列的极限点仍然隶属于闭集；③ 按连续性的点列刻画，值域空间中对应的函数序列收敛.

凹凸性(隶属自身结构) 一元函数凹凸性的本质刻画可为数型Jensen不等式：

以此可以获得若干重要的不等式.由此，可以获得结论： ① 由凹凸性可推出单侧变化率的存在性，由此基于左、右变化率的存在性可得连续性；② 由凹凸性的定义，可获得Hadamard不等式： 设f(x)在[a,b]下凸，则有

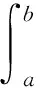
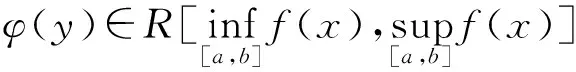
分部估计(隶属通识结构) 指基于结构，将需要估计的对象分成不同的组并分别进行估计.① 闭方块上Riemann积分的振幅和具有如下估计：

则可获得极限估计.

分离估计(隶属通识结构) 指基于结构，将构成所需估计对象的不同成分分别进行估计.① 基于Abel估计：

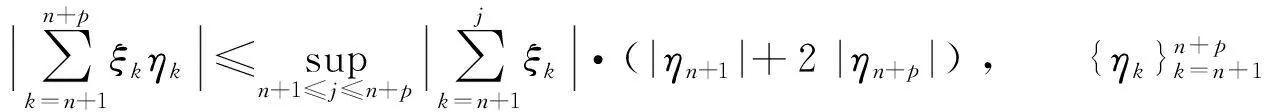
为控制右端项为小量，则可自然导出数项级数的Abel-Dirichlet判别法：

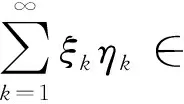
式中φ(x)Riemann可积，η(x)单调，为控制右端的两项(具有相同的结构)为小量，则可自然导出广义积分的Abel-Dirichlet判别法：

式中|δi|<ε∈+(i=1,2,…,N)，∀|P|<δε.以此结构，可说明： ① 曲线上积分，局部直线段与切线段近似的一致性；② 曲面上积分，局部平面块近似与切平面块近似的一致性；③ 基于定积分计算数列极限亦以此结构进行“简化”，表现为：

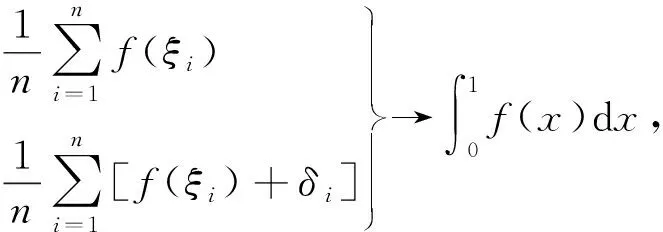
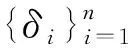
Fermat引理(隶属通识结构) 指一元函数在其极值点可导，则导数为零.Fermat引理基于极值点的定义、极限保号性以及整体极限的存在性等价于单侧极限的存在性.多元函数也具有极值点的定义，并且将函数的定义限制于直线段后仍可成立Fermat引理，对应于在极限点存在方向导数，则方向导数为零.进一步，Fermat引理可以推广到泛函的变分计算.泛函可以一般地理解为函数的函数：

C2(Ω)φ(x)，

λξ(λ)∶=A(φ*(x)+λθ(x))∈，

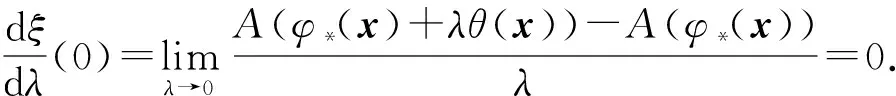
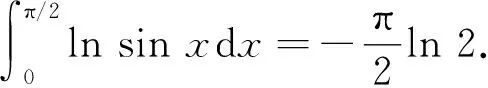
比较的思想与方法(隶属通识结构) 对于不变号级数与不变号函数广义积分的敛散性的判定，主要基于比较的思想与方法.按不变号级数与不变号函数广义积分收敛的Cauchy收敛原理：

可引入充分性估计方法：

式中λ∈+，此即“比较的思想”，形式为直接比较，ξn与φ(x)为比较的对象.按此比较方式，可以衍生出具有实际应用价值的极限形式：

上述结论具有一致的分析机制.对于正项级数，进一步可以设计间接的“比较的方式”：

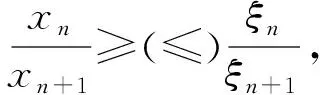
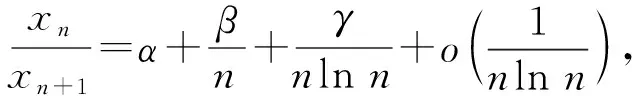
3.2.3 一元微积分与多元微积分之间的关系

单参数化设多元函数定义在m中的一个开集，在开集中确定一个直线段或者曲线段，然后研究限制于直线段或者曲线段上的多元函数，则多元函数退化为一元函数.由此，一元函数的相关结果可以延拓到多元函数，具体有： ① 直线段上连续且内部可导的多元函数的Lagrange中值定理；② 直线段上连续且内部可导的向量值映照的有限增量估计；③ 曲线段上多元函数与向量值映照的有限增量估计.上述①、②的获得基于一元函数的Lagrange中值定理；③的获得需要每一直线段上的估计与Darboux和估计相联系.

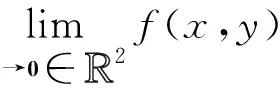
按上述分析方法可以考察极限是否路径相关；如果路径分析的结果显示路径无关，则从正面考虑极限的存在性.上述路径分析的思想在于将平面曲线局部Monge型化，在原点附近考虑曲线的局部Monge化也具有一般意义，故路径分析在考察极限是否路径相关一般较为有效.

Fubini定理与体积分换元公式高维积分学需要为面上与体上的积分计算提供方法.Fubini定理将二维及其以上区域的积分最值转化为闭区间上的积分，就此一般利用Newton-Leibniz定理；体积分换元公式则主要将几何非规则区域上的积分转换为几何规则区域上的积分，此处几何规则区域要求可以应用Fubini定理；体积分换元公式的另一作用是简化被积函数.总体而言，面上与体上的积分计算依然是化到闭区间上的积分，并未提供新的计算方法.值得指出的是，一元积分学中闭区间上的积分有换元公式，而高维积分学中体积分换元公式的本质仍在于闭区间上的积分换元公式.

3.2.4 变换的思想

微分同胚高维微分学中引入微分同胚的概念，指同维Euclid空间中两个开集之间的双射，且原映照与逆映照都具有相同的正则性.微分同胚中的2个开集，一个可谓实际的物理区域，另一个称为参数区域；两者之间的双射可以将物理区域上的分布等价于参数区域上的分布，如图5所示；原映照与逆映照都具有一定的正则性，当设定物理区域上的原分布可微时，有参数区域上的分布可微，就此基于复合向量值映照Jacobi矩阵计算的链式法则可以程序化地将物理区域上的分布所满足的偏微分方程(反映物理事件本身)转换到参数区域上的分布所满足的偏微分方程.类似于体积分换元公式，基于微分同胚一方面可以将几何不规则的物理区域上的分布转化至几何规则的参数区域上的分布，并且获得其所满足的偏微分方程；另一方面可以通过变换简化物理区域上分布的偏微分方程.值得指出的是，基于微分同胚的上述特征，在计算力学中微分同胚也称为曲线坐标或者曲线坐标系.

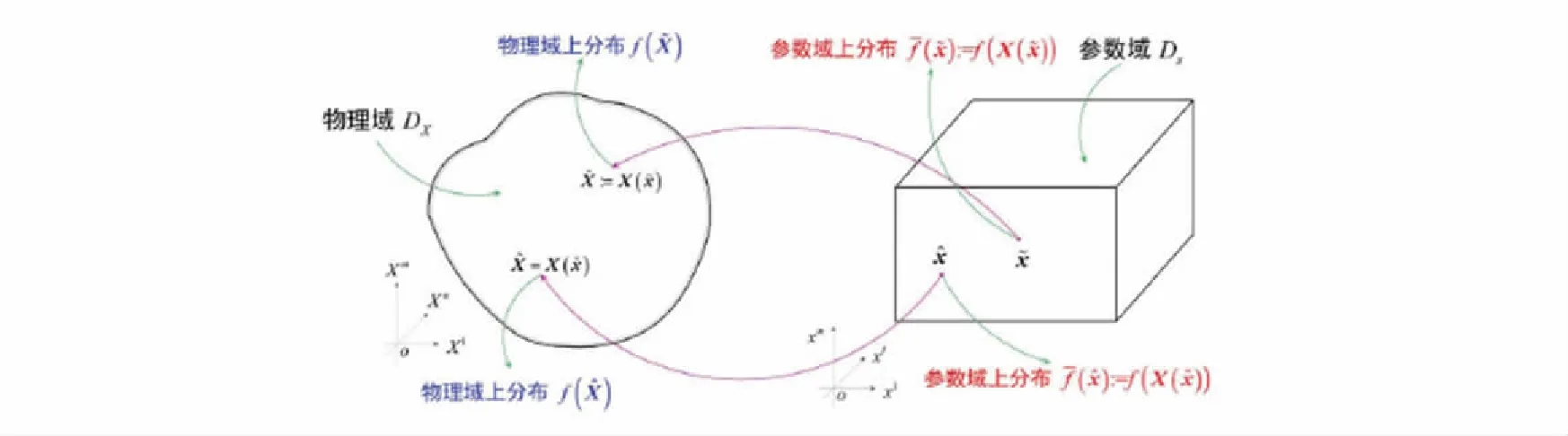
图5 高维微分学中微分同胚示意图Fig.5 The sketch of diffeomorphism in high dimensional differential calculus

秩定理对于一般的向量值映照，其自变量与因变量都可以是若干个数，由此可以理解为将一个Euclid空间中的“马铃薯”变化成另一个Euclid空间中的“马铃薯”.如果在某一点的某个邻域内，向量值映照的Jacobi矩阵具有相同的秩r，则对于自变量与因变量都可以引入新的坐标系(亦即为自变量与因变量都引入微分同胚)，在新的坐标空间中此向量值映照将自变量空间中的一个方块映照至方块的底面，就此获得了对此映照的最简单的表示.基于秩定理可以定义函数组的相关性.

Morse定理线性代数中，对称阵可以实现正交相似对角化.就此，对称阵可以理解为2个同维Euclid空间中的一种特殊的线性变换；正交相似对角化可以理解为对自变量与因变量空间引入相同的正交变换(旋转与镜像对称变换)，使得在新的自变量与因变量空间中此线性变换的变换矩阵为由特征值构成的对角阵，也就获得了对此变换的最简单的表示.对于连续可微的多元函数，对其非退化临界点的某邻域可以引入新的自变量，就此可以获得此多元函数的最简单的表示.

体积分换元公式体积分换元公式将几何不规则区域上的积分转换至几何规则区域上的积分，以至于可以应用Fubini定理将高维体积上的积分逐一转换为沿各坐标轴的闭区间上的积分.体积分换元公式的获得本质性地基于微分同胚的局部简单微分同胚的分解： 一般的微分同胚可以理解为力学中的一般变形/整体变形，简单微分同胚则是单方向的变形；对于足够小的范围，整体变形可以分解为各个方向变形的组合.对于单方向的变形，基于Fubini定理与闭区间上的积分换元公式就获得此情况的体积分换元公式.线性代数中非奇异阵可以分解为基本初等矩阵的乘积；微分学中整体变形的Jacobi矩阵可以分解为各方向变形的Jacobi矩阵的乘积.

3.2.5 因果分解

隐映照定理按模型化的观点，可以将一个事物或者事件抽象成若干要素，问题是这些要素中哪些是因，哪些是果？或者有问题是先有鸡还是先有蛋？微分学中的隐映照定理回答了上述问题，在一定的条件下，可以判断一组要素中哪些是因，哪些是果.值得指出的是，分析上可以基于压缩映照定理证明隐映照定理，以此尽管定理本身并未给出确定由因至果的解析表示形式，但数值上可以基于压缩映照通过迭代获得具体的对应关系，由此隐映照定理具有实际应用的价值.隐映照定理的结果直接说明了有限个数中哪些是因，哪些是果，其几何意义就是高维Euclid空间中曲线、曲面与抽象曲面的微分流形刻画，这也是Poincare对微分流形的基本观点[7].

约束上最值问题研究定义在体积(开集)上的分布的最值点，则基于Fermat引理： 定义在直线段上的分布在极值点存在可导，则在该点处分布关于直线段的方向导数为零；Fermat引理的实质在于对于一元函数而言存在整体极限等价于存在单侧极限、函数极限的保号性.如果所需研究的分布定义在曲面或者曲线上，则Fermat引理不能直接推广，因为此时让分布在一个直线段上有定义都做不到.为研究约束上分布的极值点，基本的方法就是对约束采用微分流形的观点，亦即局部意义上可以明确哪些Cartesian坐标是因、哪些是果，由此约束上的分布就对应为隶属因的那部分Cartesian坐标的函数，就此可以使用Fermat引理.以此为基础，基于复合向量值映照的矩阵形式的链式求导可获得约束上分布的临界点方程.值得指出的是，进一步按展开至二阶的近似以研究极值的类别可以“推导出”常用的处理约束上最值问题的Lagrange乘子法.

3.3 微积分的主要方法

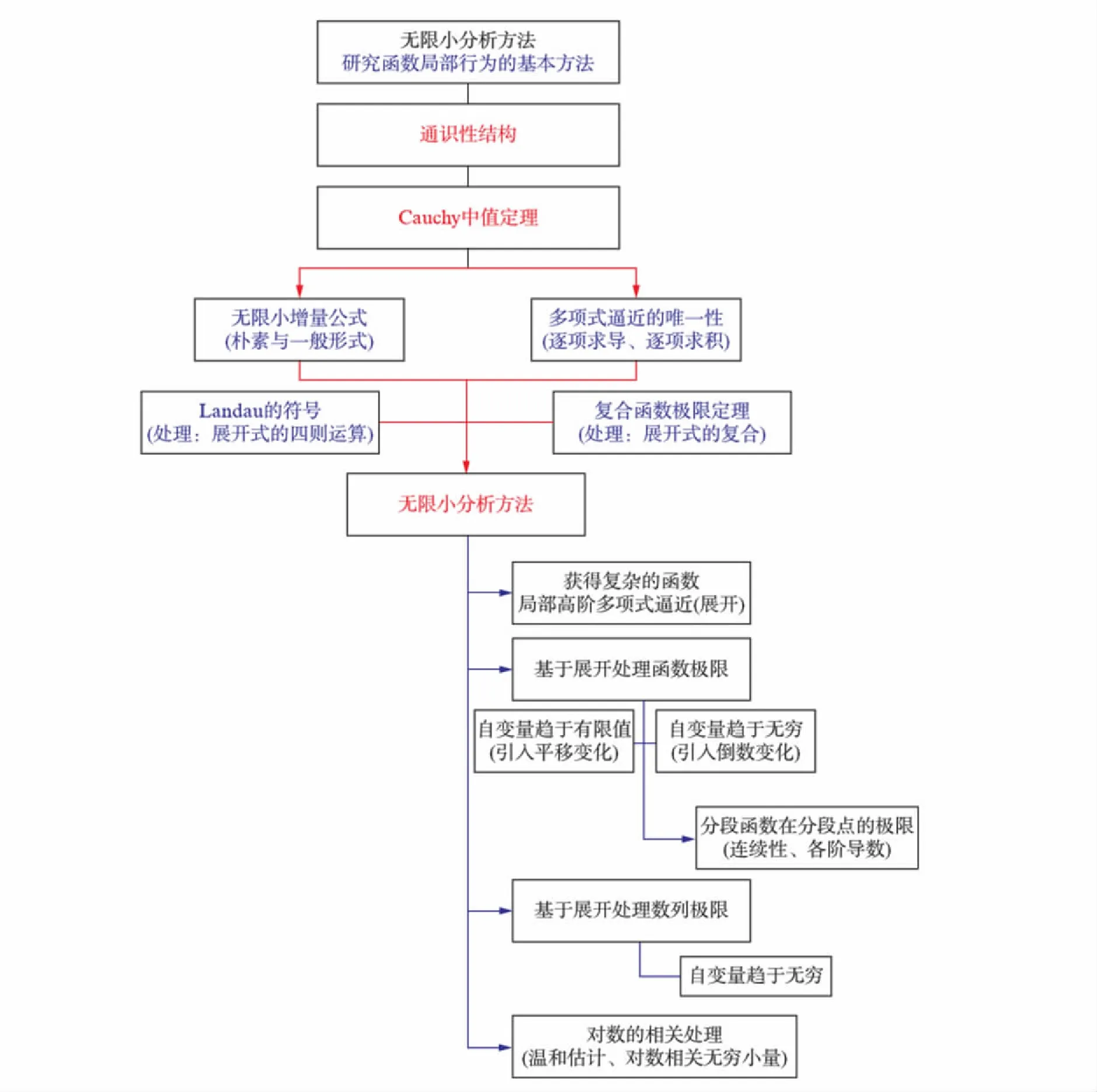
图6 知识转化为方法的事例： 无限小分析方法Fig.6 Case of the transformation from knowledge to ability： The method of infinitesimal analysis

我们不应该学习就是为了考试、考试就是为了考试、考完基本全忘记，而是应该将知识转化为认识世界的能力.就此笔者建议将知识转化为方法.所谓“方法”，指可以系统性解决一类问题的思路与做法，方法对于问题的处理具有较为清晰的相似性与指导性.获得方法的基础在于对同类问题的本质的认识，我们将“本质”称为“结构”.由于“相同的结构可以驱动不同的结论”，所以提炼可处理一类问题的方法也在于认识由结构驱动结论的具体方式.基于方法可以将知识转化为能力.能力，指对所需研究的事物首先抽象为微积分等知识体系的研究对象，然后利用对应的方法研究对应的性质，以期获得对所研究的事物的认识.

值得指出的是，一般数学教程中往往首先通过定义确定所需研究的对象，然后推导出性质、定理以表示对所需研究对象的认识.然而，性质与定理并不总是认识对象“最适合的形式”.例如，为研究一元函数的局部行为往往需要获得局部意义下的高阶多项式逼近，就此归纳无限小分析方法，如图6所示.一元微分学中有定理： 当f(x)在x0点存在p阶导数，则有局部意义下的高阶多项式：

原则上可以按上述定理获得多项式逼近，但求解高阶导数的计算量非常大.实际为获得高阶多项式逼近，往往对基本初等函数的展开利用“逐项求导”与“逐项求积”.这2个技术性引理源于上述定理与高阶多项式逼近的唯一性.对于多元函数亦有类似的结论.由此事例可见，性质与定理并不就是直接的方法.

3.3.1 一元微积分的主要方法

就一元微积分，现归纳的主要方法有下面的10类.

1) 数列极限的计算方法，包括典型的分析方法(涉及分部估计、Abel和式估计等)；引入无穷小量的做法；处理带有和式的数列极限(Stolz定理、化为定积分)；转化为函数极限处理.

2) 无限小分析方法，主要为获得函数的局部高阶多项式逼近，以此可有效处理函数极限、数列极限.方法主要包括基本初等函数的展开；技术性引理(逐项求导、逐项求积)；Landau符号的性质(表现为抓住主要矛盾忽略次要矛盾).如图6(看第260页)所示.

3) 函数导数的计算方法，包括充分性方法(四则运算、链式求导)；极限分析方法(针对分段函数).

4) 函数的定性作图方法，用于定性绘制平面Monge型曲线、一般参数曲线，涉及确定渐近线、单调区间、凹凸区间等.

5) 一致连续性的分析方法，分为有界区间与无界区间上连续函数二类情形.有界区间上连续函数的一致连续性的判定等同于判定函数是否可以连续延拓至边界点.

6) 不定积分的计算方法，包括基本方法(第一类换元法、第二类换元法、分部积分方法)；隶属有理化的换元法(涉及处理根式、三角函数的变换、Euler变换与Abel变换等)；若干基于结构的处理方法.

7) 定积分与广义积分的计算方法，定积分的计算一般基于Newton-Leibniz公式，就此需确认原函数；广义积分的积分(认定收敛)一般先获得以积分限为自变量的函数，然后再取极限；典型广义积分的计算，包括Euler积分、Froullani积分(涉及积分第一中值定理).

8) 广义积分敛散性的分析方法，可归纳判定绝对收敛性、自身收敛性、绝对发散性、发散性的判定方法，按上述分析流程可获得对绝对收敛性、条件收敛性、发散性的判定.值得指出的是，无限小分析方法在广义积分敛散性的判定中亦起到重要的作用.

9) 获得不等式的方法(包括数型、函数型、积分型不等式)，数型不等式可来源于函数的单调性、凹凸性(包括Young不等式，以此获得Hölder不等式、Minkowskii不等式、一般形式的Jensen不等式)；函数型不等式可一般地归结于最值问题，特别地可基于单调性；积分型不等式可源于对应的数型不等式(包括Hölder不等式、Minkowskii不等式、一般形式的Jensen不等式)，基于凹凸性的Hadamard不等式等；积分不等式亦可联系于变动积分限的函数，并结合积分的相关等式与不等式.

10) 函数全局行为的分析方法(包括等式与不等式、联系于广义积分收敛性的性质)，这方面的内容可以非常地广泛，需要结合问题的具体结构进行分析.例如，Rolle定理可以应用于一般函数与变动积分限的函数(共同的特点就是两端一样高)，从而获得函数与积分的等式关系；基于积分第一与第二中值定理亦可以获得积分型等式.

3.3.2 高维微积分的主要方法

就高维微积分，现归纳的主要方法有下面的12类.

1) 向量值映照/多元函数极限的计算方法，包括正向说明极限存在；基于路径分析方法(通过极限分析找出路径)说明极限不存在.

2) 向量值映照/多元函数导数的计算方法，包括充分性方法与极限分析方法.特别地,在充分性方法中所提取的矩阵形式的链式求导,对于隐映照与逆映照的导数计算非常有效.

3) 无限小分析方法，亦即获得多元函数的高阶多项式逼近的系统方法.类似于获得一元函数的高阶多项式逼近的无限小分析方法,获得多元函数的高阶多项式逼近并不是直接套用无限小增量公式,而是常常基于间接性方法.

4) 隐式形式曲线与曲面的处理方法,包括基于隐映照定理获得曲线与曲面的局部Monge表示,并基于矩阵形式的链式求导计算相关几何量.

5) 处理约束上最值问题的方法,主要基于Lagrange乘子法,包括约束上极值的类别判定.

6) 变换方程方法，按微分同胚的观点，可以引入自变量变换与因变量变换，以期简化原有因变量相对于原有自变量的偏微分方程，所归结的方法可以有效地获得新的因变量相对于新的自变量的偏微分方程.

7) 体积分计算的换元方法,基于含有零测集修正的体积换元公式,针对积分区域与被积函数,归结常用的积分换元方法.

8) 判定正项级数敛散性的方法，包括通项的基于无限小分析方法的展开、比值形式的展开及其判定方法.

9) 判定一般数项级数敛散性的方法,包括绝对收敛性、条件收敛性与发散性的分析流程与判定方法.

10) 判定函数序列与函数项级数一致收敛性的方法，主要基于最值点的位置估计.

11) 幂级数的相关方法，包括确定幂级数收敛域的方法，主要基于通项比值形式的展开；获得复杂函数的幂级数表示，主要基于幂级数的分析性质；基于幂级数分析性质的相关应用，包括微分方程的级数解法等.

12) Fourier级数的相关方法，主要基于点收敛意义的展开定理获得函数的三角级数展开，包括正弦或者余弦展开.另有，内积意义的Fourier级数展开，可在泛函分析中进行严格阐述.

基于上述所归纳的方法，可以顺利地处理吉米多维奇著《数学分析习题集》[8]中约70%～80%的题目.

4 知识体系传播的研究——追求并保证对于高程度知识体系的传播具有优秀的教学成效

4.1 知识体系传播研究的学术基础

复杂分析过程的要义分解对于数理方面的课程，学生感到困难以至于“跟不上”的主要原因在于课堂上被一些推导或者结论“卡住”，往往自己还在思考，教师已经涉及后续内容.就此可考虑“将复杂分析过程分解为若干要义”，“要义”包括： ① 分析的总体思想与方法；② 分析涉及的基础性结论；③分析涉及的特定概念与技巧.讲授时，首先澄清各个要义，然后再进行整体性的分析.对于复杂分析过程进行要义分解，亦表示了对复杂事物的认识过程与认识程度，需要尽量做到“正本清源”，揭示事物的本质.

如此处理，具有如下益处： ① 可以有效降低学生对于复杂分析过程整体性与局部性理解上的困难，提高听课的流畅性，保持学习兴趣；② 有些要义为基础性结论，就此再做澄清可起到“温故而知新”的效用.对于复杂事物，往往第一遍难以理解，但第二、第三遍就能迅速提升理解的程度.课程讲授也需要恰如其分地回顾已有的内容，不仅能“承上启下”，而且需要时再做回顾可以有效地帮助学生提高认识程度，提高学生听课的流畅性.

图7为高维积分学中Stokes公式证明的流程概要，其过程可以澄清如下： ① 基于物理空间与参数空间中边界曲线之间的关系，获得曲面参数域边界上的曲线积分；② 基于Green公式，将参数域边界上的曲线积分化成参数域上的积分；③ 通过矩阵形式链式求导，厘清参数域上的积分对应速度旋度在物理空间中曲面上的通量，此处速度旋度解释为速度Jacobi阵反称化后的对偶向量.一般教程中Stokes公式的证明往往涉及较为复杂的计算，不易澄清证明的要点.笔者设计的上述证明方法，无需将相关导数的计算具体化，并且注重所推导式子的几何与物理意义，基于上述3点在20min内就可以讲清Stokes公式的完全形式的推导，而且多数学生可以厘清脉络、澄清细节.

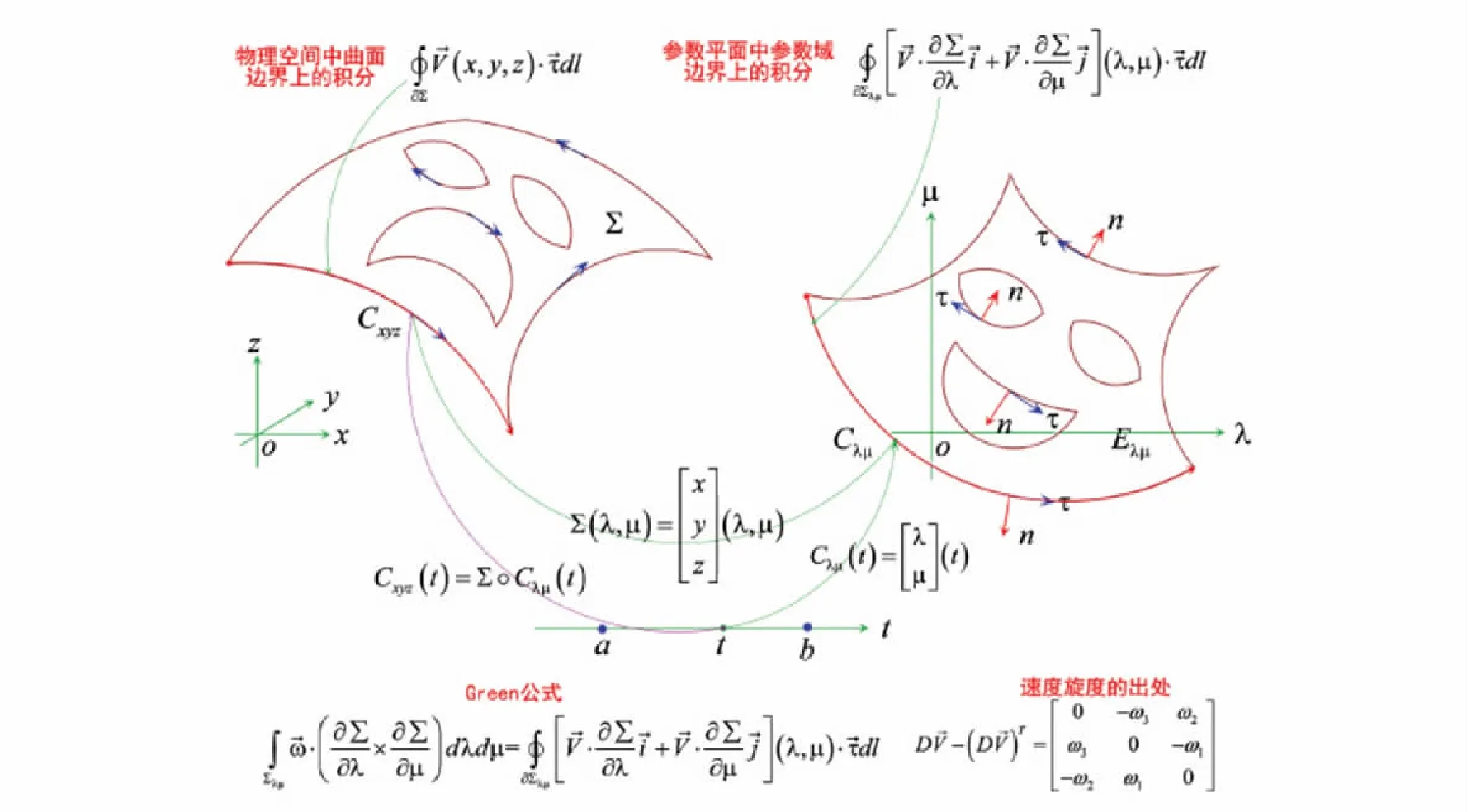
图7 复杂过程要义分解的事例： 高维积分学中的Stokes公式Fig.7 Case of essence decomposition of complex process： Stokes formula in high dimensional integral calculus

值得指出的是，微积分等数理知识体系的基本思想与方法，往往蕴含于分析过程，而非具体的结论；不同的分析过程往往也会导致不尽相同的结果.就此，数理课程需要细致剖析相关复杂分析，基于要义分解提升学生的理解程度.

教学上应该注重向学生传授基本的思想与方法，培养其具有理论联系实际的能力；而不能停留于“依葫芦画瓢”式的做题，主要为了应付考试.学习一门知识体系，如不能利用其思想与方法以认识世界、应用于生产与实践，那就失去了意义.

图示化研究我们对于图形有着与生俱来的亲和性与认同感.由此，非常值得进行知识体系的图示化研究，可以包括下面的6个方面.

① 概念的图示化

指将一般以文字阐述的概念与结论，通过图示进行表示，特别体现其几何、物理意义等.

高维微分学中向量值映照极限定义的图示化，如图8所示，展示了极限的3种刻画形式： 集聚刻画(Cauchy叙述)、点列刻画(Heine刻画)、振幅刻画(Cauchy收敛原理).值得指出的是，这种概念的图示化可以自然衍生至分析的图示化，有助于认识事物的本质.

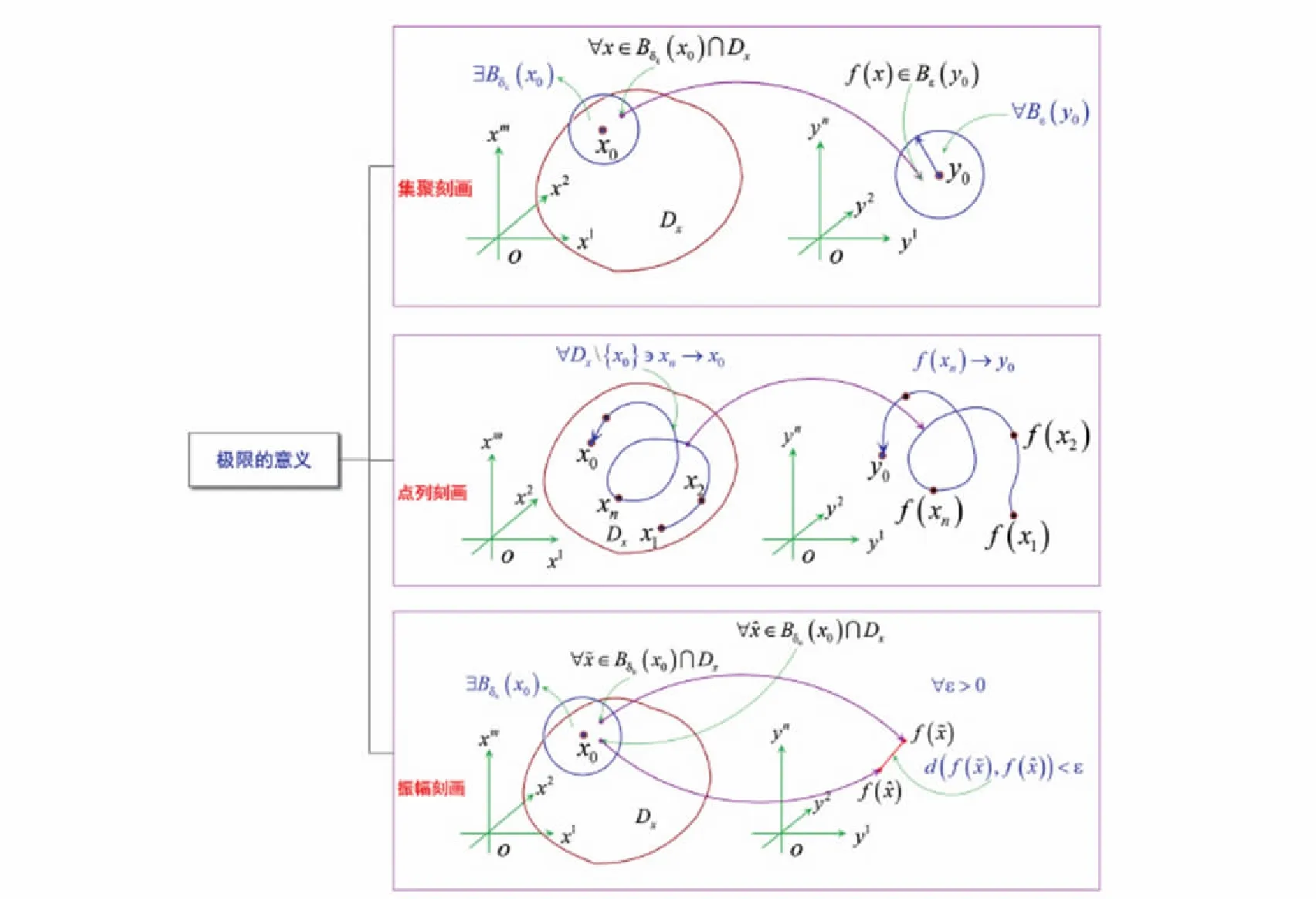
图8 概念的图示化的事例： 高维微分学中向量值映照的极限定义Fig.8 Case of graphicalization of concept： Definition of limitation of vector valued map in high dimensional differential calculus

② 结论的图示化

类似于概念的图示化，指通过图示表示相关结论.

图9所示显示了高维积分学中曲面上积分的定义.一般地，将曲面上的积分分为第一类(质量型)、第二类(通量型)曲面积分，实际流体力学中还有压力型曲面积分，而且给出了对应的计算公式.实际上，曲面上积分的“实质”就是曲面细分(通过参数域细分)之后面积微元的近似，我们现采用切平面片近似，以此就可以获得曲面上各种形式积分的定义式(部分和极限)，自然地也就获得了定义于参数域上的计算式.

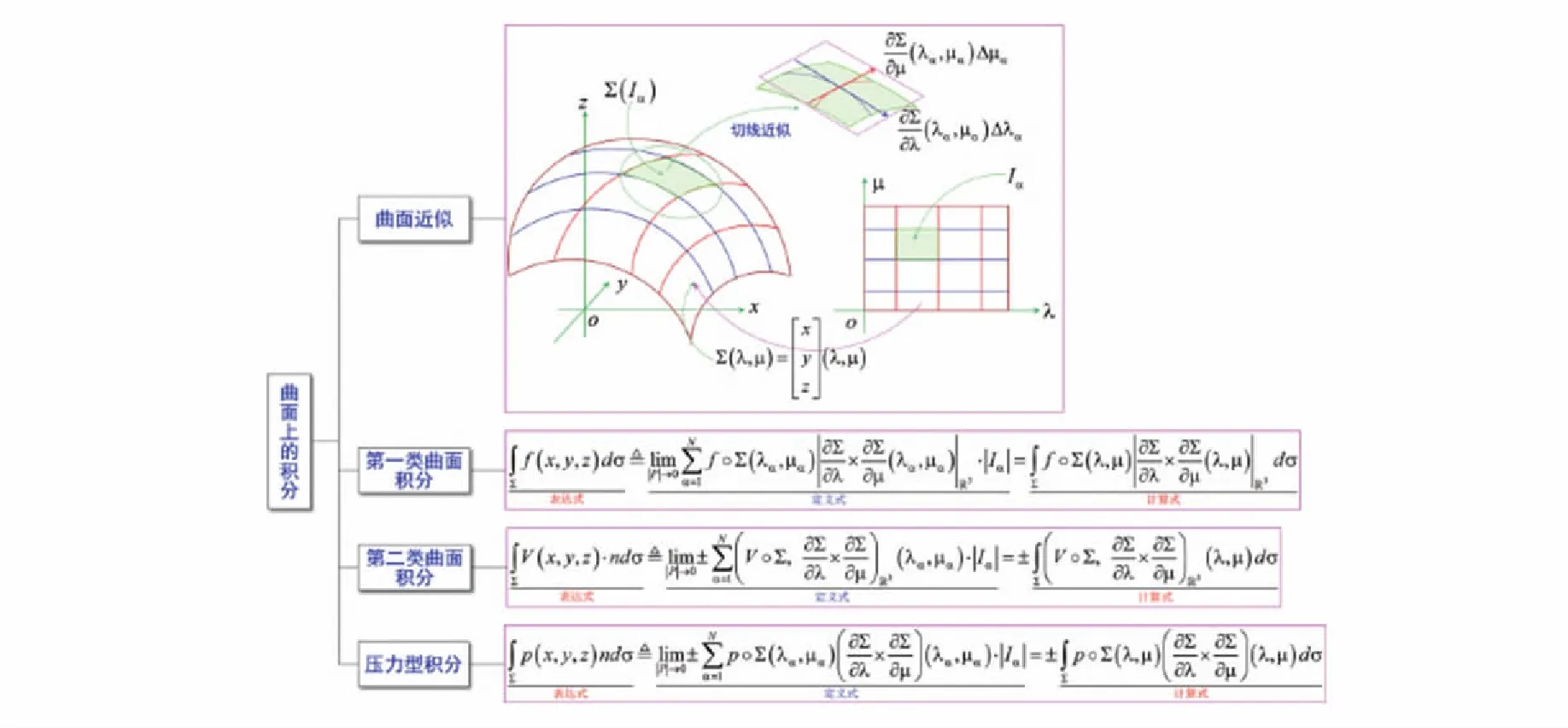
图9 结论的图示化的事例： 高维积分学中曲面上积分的定义Fig.9 Case of graphicalization of conclusion： Definition of integrals on surface in high dimensional integral calculus

③ 思想的图示化

指通过图示表现相关思想.

图10表示了高维微分学中的主要思想“直线单参数化”，将原定义于体积的多元函数或者向量值映照限制于直线段，则成为一元函数或者单参数向量值映照.由此，对限制于直线段的多元函数就可以使用一元微积分的相关处理与结论，如Lagrange中值定理、无限小与有限增量公式等，以此可以获得多元函数的Lagrange中值定理、无限小与有限增量公式等.可见，直线单参数化为将一元微积分的相关思想与方法引入多元函数的研究铺设的桥梁.某种意义上而言，高维微分学知识体系可以分为2个部分： 一部分基于直线单参数化平行地推广一元函数的相关结论；另一部分则源于高维的自身结构，如隐映照定理等.

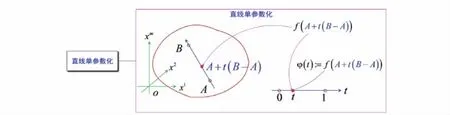
图10 思想的图示化的事例： 高维微分学中的“直线单参数化”Fig.10 Case of graphicalization of idea： Single parameterization by straight line in high dimensional differential calculus

④ 分析的图示化

我们将复杂分析过程进行要义分解，而对于要义的澄清可充分基于图示化澄清或揭示相关处理的“实质”；当然对于一般的分析过程也可以充分利用图示表现“到底是怎么回事”.看书时往往会迷惑于某句话、某一结构或者某种作法，对此往往可以在教学中通过图示澄清缘由，由此可有效地提升学生对基本思想与方法的学习效率，也让其感受到认真听讲的意义.

图11显示，零测集上修正一个Riemann可积函数(要求修正的值有界)依然Riemann可积并且积分值一样的分析实质： 零测集对应有ε-方块覆盖，以此可以做譬如2倍的ε-方块，其体积依然为小量，且对于足够细密的分割，与ε-方块相交的方块将包含于2倍的ε-方块.值得指出的是，上述分析实质上也同样服务于Lebesgue定理的证明.

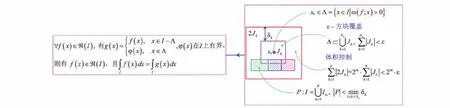
图11 分析的图示化的事例： Riemann可积函数的基本性质Fig.11 Case of graphicalization of analysis： Essential property of Riemann integrable function

⑤ 方法的图示化

我们注重归纳与提取可以解决一类问题的系统性方法.由此，学生在做练习时就“有章可循”，初步实践“理论联系实践”，而不是“就为了做题目而做题目”，似乎“学习就为了做题为了考试”.值得指出的是，学习期间通过做题可以理解、掌握并进一步优化所归纳的方法，从而今后在工作上就有能力运用方法.值得指出的是，微积分知识体系不仅是其他数理知识体系的基础，而且为认知世界提供了系统且深入的思想与方法.

类比于一元积分学中对于不定积分的获得，我们可以就有理化的处理归类若干种换元方法，对体积上的积分也可以主要根据积分域的几何特征构造若干种换元形式，如图12所示.值得指出的是，所有的换元都遵循具有零测集修正的积分换元公式.

图12 方法的图示化的事例： 体积分中换元的典型形式Fig.12 Case of graphicalization of method： Typical transformations of variables in volume integral valuables

⑥ 架构的图示化

指基于框图表示知识体系的知识点及其知识要素，就此可清晰呈现整个知识体系的脉络，包括数学通识.学生进行阶段性或者期末总结时可以利用知识体系架构既进行“查漏补缺”，亦建立总体性的认识.

值得指出的是，数理课程教学上，可基于板书充分地进行概念与分析过程的图示化阐述，不仅可以使得课程讲授生动、清晰而避免乏味的照本宣科，而且可以深入地揭示事物的本质.

值得指出的是，复杂过程的要义分解、图示化研究都主要基于对知识体系自身的系统且深入的研究；由此课堂讲授大量反映教师自身的认识与体会，这不仅能吸引学生的注意力，而且有利于学生基于教师的认知而获得“事半功倍”的学习成效——这也是笔者传播数理知识体系的主要追求.

4.2 在线资源

4.2.1 课程体系网站

为配合微积分教学，笔者建设有课程体系网站： 微积分的一流化进程(http：∥fdjpkc.fudan.edu.cn/d201353/main.htm).

本课程体系网站的建设基于微积分相关数理知识体系的研习，表现在2个方面： ①知识体系自身的研究，主要特征为基于“数学通识”实现同一知识体系内的融会贯通、不同知识体系之间的触类旁通；②知识体系传播的研究，既包括研究高成效的传授方式，也包括通过组合相关知识体系以建设相关课程.

本网站涉及的知识体系及其所属课程，如图13所示.

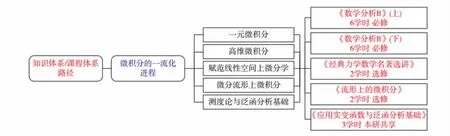
图13 “微积分的一流化进程”涉及的知识体系及其所属课程Fig.13 Knowledge systems with related courses belonging to “the progress of pursuing the first-class degree of calculus teaching”

本课程体系网站，主要包括的栏目有下面7块.

研究背景包括“数理观点”、“教学理念与教学方式”、“知识体系与课程体系”、“课程教师与合作专家”.

体系讲稿主要按知识体系发布对应的讲稿，包括“Euclid空间上微积分”、“微分流形上微积分”、“赋范线性空间上微分学”、“测度论”、“泛函分析”.后2个目录尚在建设中.

教学视频主要按知识体系发布对应的教学视频，包括一元微分学，一元积分学；常微分基础；高维微分学(基础层面、高级层面、应用事例)，高维积分学(基础层面、高级层面、应用事例)，级数；流形上微分学，流形上积分学；赋范线性空间上微分学；测度理论，可测函数，积分理论；度量空间，内积空间；Sobolev空间；Fourier分析；渐近分析.测度论、泛函分析部分尚在建设中.

课程建设通过组合相关知识体系建设相关课程，包括： “数学分析”(一年制)，“经典力学数学名著选讲”(有关微积分的深化)；“流形上的微积分”，“应用实变函数与泛函分析基础”(本科生与研究生共享课程).对于每一课程，包括子栏目： 知识体系、教学大纲、试卷习题、教与学研究、开设信息.

教学研究综合性包括： “阶段总结”；“杂志论文(含原稿)”，“会议论文(含原稿)”；“学术报告(含随笔)”；“教改项目”.

图示研究致力于将数理知识体系中重要的概念、复杂的分析过程进行图示化说明.图示化研究成果源于并服务于知识体系自身的研究，亦隶属并服务于知识体系传播的研究.按知识体系建设相关目录，包括“Euclid空间上微积分”，“微分流形上微积分”；“赋范线性空间上微分学”；“测度论”；“泛函分析”.目前主要涉及“Euclid空间上微积分”的图示化研究，其他的均在建设中.

通识研究隶属同一知识体系或者不同知识体系的知识点可能含有相同的“数学通识”——特定的数学等式、不等式或者特定的处理方式方法；基于“数学通识”可实现同一知识体系之间的“融会贯通”，不同知识体系之间的“触类旁通”.本栏目设计为按知识体系划分子目录以分别进行通识性结构的研究，并在对应的子栏目下涉及跨知识体系的通识性结构的研究.本栏目还在持续性建设中.

基于课程体系网站，我们将课堂的功能分为两个递进性层面，如图14所示.

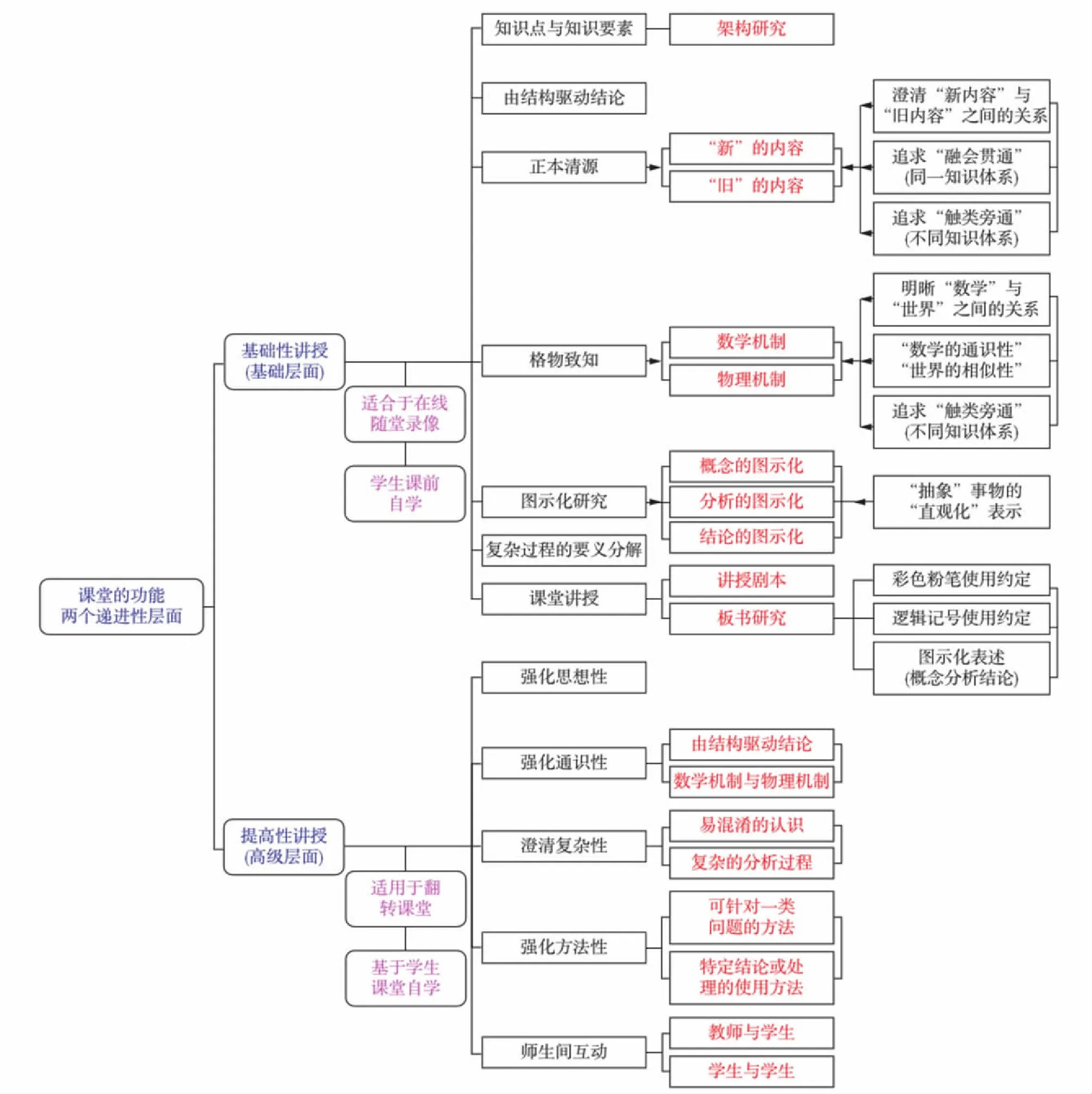
图14 课堂的功能(两个递进性层面)： 基础性讲授(基础层面)、提高性讲授(高级层面)Fig.14 Functions of class(two progressive levels)： Elementary teaching(elementary level), advanced teaching(advanced level)

①基础性讲授(基本层面) 基于我们现有的对知识体系自身及其传播的研究，系统且清晰地讲授相关思想与方法.这种类型的教学视频可供学生初始的自习.

②提高性讲授(高级层面) 学生事先学习了基础性层面的教学视频，就此课堂讲授不再是强调与重复所有的“细枝末节”，而是强化思想性、强化通识性、澄清复杂性、强化方法性，并且课堂形式可以增加师生间的互动，提高课堂的翻转性.

笔者自2011年起基于复旦大学精品课程网站(http：∥fdjpkc.fudan.edu.cn/)建设本课程体系网站.本网站所有信息可在全球范围浏览，故目前除了校内学生使用，校外甚至国外都有学习者，偶尔会收到他们的来信，多为赞许以及期许发布进一步的内容.

4.2.2 在线课程

基于课程体系网站的建设经验与体会，笔者自2015年起基于复旦大学在线课程平台建设《数学分析——一元微积分》、《数学分析——高维微积分》两门目录，目前已近完成；计划于2017—2018学年正式使用.

现在线课程提供的主要学习资料为：

课程录像分为随堂录像与概述录像两部分： ① 随堂录像注重循序渐进、讲述细致，应用于初始学习；② 概述录像注重整体性阐述相关思想与方法，应用于阶段性学习.一般而言，经过2至3次的学习可以理解与掌握数学分析的基本思想与方法.学习视频一般对应于随堂录像，观看此类视频，并结合学习目的中所列的要点掌握基本的概念、思想与方法.

学习讲稿为在线PDF文本，已出版的教材《微积分讲稿——一元微积分》、《微积分讲稿——高维微积分》包括这些讲稿的主要内容.学习讲稿主要包括： ① 阐述概念、思想与方法，基本对应于课程录像的内容；② 典型事例，往往首先为解答一类问题提供方法，然后给出代表性事例的解答.在学习概念、思想与方法之后，学习典型事例的解答.

基础练习在线PDF文本.在学习讲稿的基础上，进行相关练习.有些章节的练习分为两部分： ① 基础性练习，基于所归纳方法，可以较为轻松地解答这部分练习，作为对相关思想与方法最为初步的理解，这部分练习往往要求全部完成；② 提高性练习，这部分练习涉及较为深入的分析方法或者联系于其他知识体系.解答这部分问题往往需要一定的思考，可以多次考虑相关问题.这部分练习可以结合自己的实际情况进行选择.

图示化研究我们可将微积分中的概念、思想、结论、分析、方法进行图示化.在完成学习视频、学习讲稿、基础练习的基础上，学习图示化研究的有关内容，以期总体性理解与掌握相关思想与方法.另外有知识体系架构的图示化，以此一方面可以检查哪些内容已掌握、哪些内容尚需掌握，另一方面可以总体性研究各知识要点之间的关系.

具体的学习路径如图15所示.基于在线课程，笔者研究与实践数学分析的混合式教学模式.原则上，学生可基于上述内容循序渐进地进行自学.

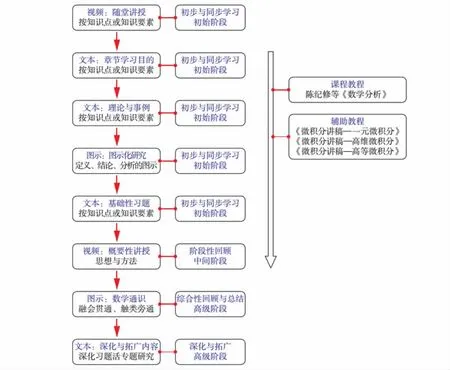
图15 在线课程各章节的内容架构，对应于学习路径Fig.15 Content framework of online course that is corresponding to the route of study

5 课程教学的两个方面

如前文所述，教学可以有两个方面： 对知识体系自身的研究和对知识体系传播的研究.上好一门课程，可以分为两个方面： “课堂上能讲些什么”和“课后能做些什么”.

5.1 课堂上能讲些什么

课堂上追求在方法论层面传授知识(思想与方法)，表现为： ① 可清晰地展现知识体系的架构/来龙去脉；② 可清晰地的阐述相关思想与方法，注重归纳可适用于一类问题的方法；③ 注重基于结构驱动结论，结构指知识体系的内在本质，往往可基于共同的结构驱动/衍生出诸多结论；④ 注重知识体系的内在相似性/通识性，以此可充分利用已有的知识认识与发展新的知识.

在方法论层面传授知识既有益于追求教与学的高成效，也有益于培养学生理论联系实际的能力，以此有助于学生将知识升华为能力.理解与把握思想与方法的能力，亦将有助于理解政治思想与理论.政治思想与理论隶属哲学范畴，实际应用时需要理论联系实际，而不是生搬硬套.按笔者的现有认识，微积分的分析思想可以包括： “抓住主要矛盾忽略次要矛盾”、“由结构驱动结论”，通过诸多实际事例的实践，可以让学生切实地体会理论联系实际的意义.

数理知识体系理应遵循辩证唯物主义.就此，一方面对于各门数理课程的学习对应于实践辩证唯物主义，以此逐步深化对辩证唯物主义的认识；另一方面可基于辩证唯物主义引领各门数理课程，有助于数理知识体系的融会贯通、触类旁通，实现由知识到能力的深华.

5.2 课后能做些什么

首先，笔者谨认为对于中国最好的一批大学，面对中国最好的一批学生，结合双一流建设，我们必须要求课程的广度与深度能类比国内外一流水平，甚至有所超越.就此，需要教师对知识体系进行持续性的研究与实践，由此教学研究的实质在于对知识体系自身的研究，以此支撑在方法论层面传授思想与方法.值得指出的是，课程广度与深度的一流化水平对于培养一流化的人才具有基础性或者实质性的意义.

对于这种高程度的教学，可以对“数学分析”课程开始实施“课程工程”，指将整个课程教学归结为： ① 实体教学，包括实体课堂、习题课；② 在线教学，包括课程体系网站与在线课程；③ 文本支持，包括教材、讲稿；④ 研讨课与研讨日志；⑤ 课程讲座.其中，实体教学是常见的课程模式.在线教学，主要通过课程体系网站、在线课程提供在线支持，学生可以结合自己的情况进行在线学习.文本支持，主要配合实体教学与在线教学，教师应该结合教学研究与实践的经验实时更新讲稿，并值得在一定积累上出版自己的教材.研讨课，在于通过研讨激发学生自主学习的成效、在于面对面的答疑解惑；研讨课可由教师与助教合作完成.另一方面，在线课程结合研讨课可以开展混合式教学.课程讲座，主要向更多的学生分享知识体系自身研究的成果.

值得指出的是，上述课程教学的两个方面充分体现了任课教师的职业风范与敬业精神，在教师言传身教的过程中可以潜移默化地影响学生养成正确的世界观、人生观与价值观，促使他们追求高尚品德，摒弃精致利己、唯利是图的不良品行.藉此，数学分析课程可具有课程思政的属性.

6 总结及讨论

本文阐述笔者十余年来在复旦大学为追求微积分的一流化教学所归纳的现有认识与体会.核心理念为教学的首要基础在于学术研究或者学术属性，然后才是敬业精神与具体的方式与方法.教学的学术属性，一方面在于对知识体系自身的研究，具体研究内容归纳有知识点与知识要素、数学通识与相似结构、正本清源、格物致知，并提出将知识转化为方法；另一方面，教学的学术属性也构成传播研究的基础，具体研究内容归纳有复杂分析过程的要义分解、图示化研究.值得指出的是，知识体系自身的研究是知识体系传播的研究的基础，前者决定后者.基于教学的学术属性，可以构建多种传播方式，包括课程体系网站、在线课程等，本文就此进行了相关阐述.

作为上述理念的具体实践，本文阐述了课程教学的两个方面： “课堂上能讲些什么”和“课后能做些什么”.上好一门课虽然以学术属性为基础，敬业精神与高成效的方式与方法也是必不可少，但做得好二者可以相辅相成、相得益彰.基于课程教学的两个方面，本文亦指出课程思政也是任何一门优秀课程的自然属性.

参考文献：

[1] ZORICH V A. Mathematical analysis (Vol.1, 2) [M]. Berlin Heidelberg： Springer-Verlag, 2004.

[2] 谢锡麟.“正本清源”在力学之教学及专业基础知识体系建立中的作用 [J].力学季刊，2012，33(4)： 544-557.

[3] 谢锡麟.可作为一种世界观的数理观点 [M]∥吴晓明.书院的理念与探索——复旦大学书院讲演录.上海： 复旦大学出版社,2016： 79-91.

[4] 谢锡麟.微积分讲稿——一元微积分 [M].上海： 复旦大学出版社,2015.

[5] 谢锡麟.微积分讲稿——高维微积分 [M].上海： 复旦大学出版社,2017.

[6] 谢锡麟.现代张量分析及其在连续介质力学中的应用 [M].上海： 复旦大学出版社,2014.

[7] ARNOLD V I. On mathematical education [J].RussianMathSurveys, 1998，53(1)： 229-236.

[8] (俄)吉米多维奇.数学分析习题集(根据2010年俄文版翻译) [M].李荣涷，李植译.北京： 高等教育出版社，2010.