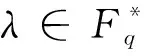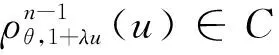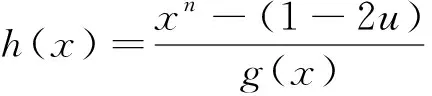环Fq+uFq+vFq+uvFq上的斜常循环码
2018-06-07陈法龙宋贤梅
陈法龙, 宋贤梅
(安徽师范大学 数学与统计学院,安徽 芜湖 241003)
有限环上的循环码理论,由于其有丰富的代数结构以及容易译码的特点,而受到众多编码工作者的青睐。但是其研究的环均是交换环,在文[1]中,Boucher等人引入了非交换环Fq[x;θ]上的循环码,举例说明在同样参数下斜循环码的汉明距离大于已知最好的线性码。随后,他们又研究了Galois环上的斜常循环码[2]。在文[3]中,Jitman等人研究了有限链环上的斜常循环码,得到了一些有意义的结果。
最近,有限非链环上的斜循环码也有了一定的研究进展。在文[4]中,Gursoy等人用不同的方法构造出环Fq+vFq(v2=v)上的斜循环码。随后,施敏加等人从更广的角度给出了有限非链环Fq+vFq+v2Fq(v3=v)[5]以及环Fq+uFq+vFq+uvFq(u2=u,v2=v,uv=vu)上的斜循环码[6]。
本文受文献[3]与[6]的启发,讨论了非链环Fq+uFq+vFq+uvFq上的斜常循环码,给出了该环上斜常循环码的结构和性质,讨论了|〈θ〉|=2时其厄米特对偶码生成多项式的形式。
1 预备知识
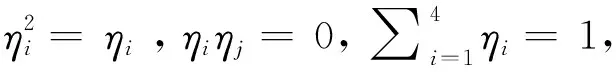
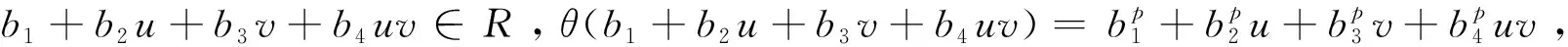
对环R上的自同构θ,形式多项式集合R[x;θ]={c0+c1x+…+cn-1xn-1|ci∈R,i=1,2,…,n-1,n≥1}构成一个非交换环,其加法运算为多项式的一般加法,乘法运算定义为(axi)(bxj)=aθi(b)xi+j,(a,b∈R)。
设Rn={(a0,…,an-1)|ai∈R,i=0,1,…,n-1}。若C是Rn的非空子集,称C是长为n的码,若C是Rn的R-子模,称C是长为n的线性码,它的多项式定义为{c0+c1x+…+cn-1xn-1|(c0,…,cn-1)∈C}。
设C是R上长为n的线性码,我们定义
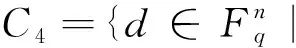
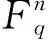
设x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈Rn,定义x与y的厄米特内积为〈x,y〉H=x1θ(y1)+x2θ(y2)+…+xnθ(yn)。
码C的厄米特对偶码定义为C⊥H={x∈Rn|〈x,y〉H=0,∀c∈C},若码C满足C=C⊥H,则称C是厄米特自对偶。
2 环R上的斜常循环码
定义2.1设θ是R上的自同构,λ是R的单位。ρθ,λ是Rn上的自同态且满足
ρθ,λ((c0,c1,…,cn-1))=(θ(λcn-1),θ(c0),…,θ(cn-2)),
则称ρθ,λ是θ-λ-常循环移位。设C是R上长为n的线性码,若对任意的c=(c0,c1,…,cn-1)∈C,有ρθ,λ(c)∈C,称码C为斜常循环码或θ-λ-常循环码。
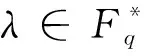
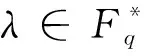
证明(⟹)设C是斜常循环码,则对任意的c=(c0,c1,…,cn-1)∈C,有
(θ((1+λu)cn-1),θ(c0),…,θ(cn-2))∈C,
即x·c(x)=θ(c0)x+…+θ(cn-2)xn-1+θ(cn-1)(1+λu)∈C,注意到C是线性的,则对任意的r(x)∈R[x;θ]/〈xn-(1+λu)〉,均有r(x)c(x)∈C成立,故C是R[x;θ]/〈xn-(1+λu)〉的左理想。
(⟸)若码C是R[x;θ]/〈xn-(1+λu)〉的左理想,则对任意的c(x)=c0+c1x+…+cn-1xn-1∈C,有
x·c(x) =θ(c0)x+θ(c1)x2+…+θ(cn-2)xn-1+θ(cn-1)xn
=(1+λu)θ(cn-1)+θ(c0)x+θ(c1)x2+…+θ(cn-2)xn-1
=θ((1+λu)cn-1)+θ(c0)x+θ(c1)x2+…+θ(cn-2)xn-1∈C,
即对任意的c=(c0,c1,…,cn-1)∈C,有(θ((1+λu)cn-1),θ(c0),…,θ(cn-2))∈C,故C是θ-(1+λu)-常循环码。
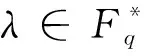
证明对任意c(x)∈C,存在q(x),r(x)∈R[x;θ]/〈xn-(1+λu)〉,满足c(x)=q(x)·g(x)+r(x),其中r(x)=0或deg (r(x)) 下证g(x)是xn-(1+λu)的右因子。对于多项式xn-(1+λu),存在q′(x),r′(x)∈R[x;θ],满足xn-(1+λu)=q′(x)g(x)+r′(x),其中r′(x)=0或deg (r′(x)) 证明对任意的r=(r0,r1,…,rn-1)∈C,记ri=η1ai+η2bi+η3c3+η4di,其中ai,bi,ci,di∈Fq,0in-1。令a=(a0,a1,…,an-1),b=(b0,b1,…,bn-1),c=(c0,c1,…,cn-1),d=(d0,d1,…,dn-1),则a∈C1,b∈C2,c∈C3,d∈C4。从而有 ρθ,1+λu(r) =(θ((1+λu)rn-1),θ(r0),…,θ(rn-2)) =(η1θ(an-1)+η2θ((1+λ)bn-1)+η3θ((1+λ)cn-1)+η4θ(dn-1),η1θ(a0)+η2θ(b0) +η3θ(c0)+η4θ(d0),…,η1θ(an-2)+η2θ(bn-2)+η3θ(cn-2)+η4θ(dn-2)) =η1(θ(an-1),θ(a0),…,θ(an-2))+η2(θ((1+λ)bn-1),θ(b0),…,θ(bn-2))+ η3(θ((1+λ)cn-1),θ(c0),…,θ(cn-2))+η4(θ(dn-1),θ(d0),…,θ(dn-2)) =η1ρθ,1(a)+η2ρθ,1+λ(b)+η3ρθ,1+λ(c)+η4ρθ,1(d)。 则C是R上长为n的θ-(1+λu)-常循环码⟺ρθ,1+λu(r)=η1ρθ,1(a)+η2ρθ,1+λ(b)+η3ρθ,1+λ(c)+η4ρθ,1(d)∈C⟺ρθ,1(a)∈C1,ρθ,1+λ(b)∈C2,ρθ,1+λ(c)∈C3,ρθ,1(d)∈C4⟺C1,C4是Fq上长为n的斜循环码,C2,C3是Fq上长为n的θ-(1+λ)-常循环码。 证明由定理2.4可知C1,C4是Fq上长为n的斜循环码,C2,C3是Fq上长为n的θ-(1+λ)-常循环码,从而有Ci=〈gi(x)〉,|Ci|=qn-deg (gi(x)),gi(x)|xn-1,i=1,4。gi(x)|xn-(1+λ),i=2,3。由于C=η1C1⊕η2C2⊕η3C3⊕η4C4,于是 证明由定理2.5知,可设C=〈η1g1(x),η2g2(x),η3g3(x),η4g4(x)〉,其中gi(x)是Ci的生成多项式。令g(x)=η1g1(x)+η2g2(x)+η3g3(x)+η4g4(x),易知〈g(x)〉⊆C。另一方面ηigi(x)=ηig(x),则C⊆〈g(x)〉,故C=〈g(x)〉。 由于gi(x)|xn-1,i=1,4。gi(x)|xn-(1+λ),i=2,3,则存在fi(x)∈Fq[x],i=1,2,3,4,使得 xn-1=f1(x)g1(x),xn-(1+λ)=f2(x)g2(x) xn-(1+λ)=f3(x)g3(x),xn-1=f4(x)g4(x) 从而有 故g(x)是xn-(1+λu)的右因子,而g(x)的唯一性可由gi(x)的唯一性得到。 由引理2.2和定理2.6容易得到以下推论。 由于限制在厄米特内积下,我们考虑当|〈θ〉|=2时的斜常循环码的厄米特对偶码。注意到|〈θ〉||n,因此本部分中的n均为偶数。 即 于是(1+λu)〈ρθ,(1+λu)-1(v),u〉H=0,因此ρθ,(1+λu)-1(v)∈C⊥H,即C⊥H是θ-(1+λu)-1-常循环码。反过来注意到(C⊥H)⊥H=C,因此得证。 特别地,若λ=-2,则1-2u=(1-2u)-1,则可以直接得出结论。 引理3.2假设θ2=1,a(x)=a0+a1x+…+an-1xn-1,b(x)=b0+b1x+…+bn-1xn-1∈R[x;θ],则下面的几条性质等价: (1)对任意的i∈{0,1,…,n-1},a(x)系数向量厄米特正交于xiφ(xn-1φ(b(x)))的系数向量。 (2)(a0,a1,…,an-1)与(θn-1(bn-1),bn-2,…,θn-2(b0))以及它的θ-(1-2u)-常循环移位厄米特正交。 (3)在R[x;θ]/〈xn-(1-2u)〉中,a(x)b(x)=0。 则(1)斜多项式φ(xdeg (h(x))φ(h(x)))是xn-(1-2u)的右因子。 (2)C⊥H是由φ(xdeg (h(x))φ(h(x)))生成的θ-(1-2u)-常循环码。 证明(1)由|〈θ〉||n且θ(1-2u)=1-2u,则 φ(g(x))(2u-1)(xn-deg (h(x)))(xdeg (h(x)))φ(h(x)) =φ(g(x)(2u-1))xn(φ(h(x))) =(2u-1)φ(g(x))φ(h(x))xn =(2u-1)φ(h(x)g(x))xn =(2u-1)φ(xn-(1-2u))xn =(2u-1)(x-n-(1-2u))xn =xn-(1-2u)。 则有φ(φ(g(x))((2u-1)xn-deg (h(x)))φ(xdeg (h(x))φ(h(x))))=φ(xn-(1-2u))=xn-(1-2u),从而φ(xdeg (h(x))φ(h(x)))是xn-(1-2u)的右因子。 (2)由于g(x)h(x)=0∈R[x;θ]/〈xn-(1-2u)〉,根据引理3.2得 〈φ(xdeg (h(x))φ(h(x)))〉⊆C⊥H, 注意到φ(xdeg (h(x))φ(h(x)))是xn-(1-2u)的右因子,则有 |〈φ(xdeg (h(x))φ(h(x)))〉|=|R|n-deg (h(x))=|C⊥H|, 因此〈φ(xdeg (h(x))φ(h(x)))〉=C⊥H。 参考文献: [1] BOUCHER D,GEISELMANN W,ULMER F.Skew cyclic codes [J].Appl Algebra Eng Comm Comput,2007,18(4):379-389. [2] BOUCHER D,SOLE P,ULMER F.Skew constacyclic codes over Galois rings [J].Adv Math Commun,2008,2(3):273-292. [3] JITMAN S,LING S,UDOMKAVANICH P.Skew constacyclic codes over finite chain ring [J].Adv Math Commun,2010,6(1):39-63. [4] GURSOY F,SIAP I,YILDIZ B.Construction of skew cyclic codes overFq+vFq[J].Adv Math Commun,2014,8(3):313-322. [5] SHI M,YAO T,ALAHMADI A,et al.Skew cyclic codes overFq+vFq+v2Fq[J].IEICE Trans Fund Electr,2015,E98A(8):1845-1848. [7] SIAP I,ABUALURB I,AYDIN N,et al.Skew cyclic codes of arbitrary length [J].Int J Inf Coding Theory,2011,2(1):10-20. [8] BOUCHER D,ULMER F.Coding with skew polynomial ring [J].J Symb Comput,2009,44(12):1644-1656. [9] DINH H,LOPEZ-PERMOUTH S R.Cyclic and negacyclic codes over finite chain rings [J].IEEE Trans Inform Theory,2004,50(8):1728-1744.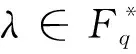
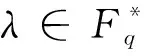
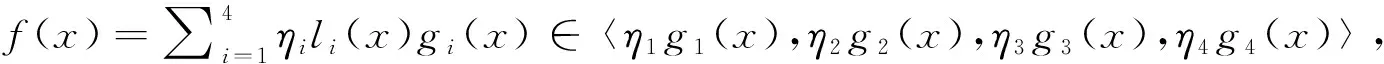
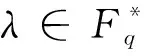
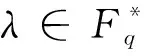
3 斜常循环码的厄米特对偶码