刘祾,武晔虹

(山西医科大学 基础医学院物理教研室,山西 太原 030001)

0 引言

基于众多的实践经验,人们归纳出量子力学的五个基本公设,包括:波函数公设，算符公设，测量公设，薛定谔方程公设和全同性原理公设[1],它们构成整个量子力学体系的逻辑框架,是微观体系研究的基本出发点。其中算符公设和测量公设要求任一力学量算符为厄米算符,而这些厄米算符的测量结果必为实数。然而最近的一些研究讨论了非厄米量子力学及其自洽理论[2-9]。特别是一类满足宇称和时间反演组合(PT)对称性的非厄米系统,由于在某些参数区域内具有完全实数的本征能量[3],使得这类系统在诸多领域已经成为研究热点。在实验上,模拟具有PT对称性的非厄米格点系统已经在光学系统[10-18]、声学系统[19-20]和电子线路系统[21]中实现。

拓扑绝缘体系统在体能隙中存在导电性的边界模,并且微扰的无序无法破坏其边界模,使其具有极为广阔的应用前景。最简单的拓扑绝缘体系统是Su-Schrieffer-Heeger(SSH) 模型,即一维聚乙炔模型[22],它具有两周期调制的跃迁强度。尽管这一模型哈密顿量具有极为简单的形式,但是它展示了丰富的物理现象,比如拓扑孤子激发,分数电荷和非平庸的边界模等[23-32]。SSH模型最主要的特征是存在两个拓扑不等价的相,可以通过在开边界条件下观察是否具有二重简并的边界模以及贝里相位来区分。在本文中我们研究当SSH模型中引入增益和损耗平衡的化学势后系统的拓扑性质。

1 模型哈密顿量

我们考虑SSH模型,其化学势虚部具有PT对称性的形式,即在每个原胞边界两端分别引入平衡的耗散和增益的化学势。这个模型哈密顿量可以写作为:

(1)

(a)λ=0.95;(b)λ=1.0;(c)λ=1.05.Here, Δ=0.5,φ=0 and λPT=1.Fig.1 Real parts (left panel) and imaginary parts(right panel) of energy in momentum space(a)λ=0.95; (b)λ=1.0; (c)λ=1.05。这里Δ=0.5,φ=0和λPT=1图1 能量在动量空间中的实部(左列)和虚部(右列)

(2)

2 结果和讨论

首先，我们研究在周期边界条件下,具有复耗散和增益势调制的SSH模型的性质。系统的哈密顿量在动量空间中可以由方程(2)所描述,它是一个两带模型,其本征能量为:

(3)

我们定义系统的所有能量都为实数时为PT未破缺区域,而当本征值能量中成对地出现实部为零且虚部能量对偶时,为PT破缺区域。它们分属不同的相区,它们的分隔点称为PT对称性破缺点,其特点为当系统参数小于此点参数时,能量无虚部,而大于此点时,系统开始出现成对的虚部,且对称地分布于零点两侧。由上式我们可以总结出PT对称性破缺点为λPT=2|Δcosφ|,即当λ<λPT时,为PT对称性未破缺区域,在此区域中系统的能量都为实数(如图1(a)),然而，当λ>λPT时,PT对称性被破缺。在转变点位置,本征值的实部的能隙关闭,并且一对虚能量开始出现。如图1所示(Δ=0.5,φ=0),随着λ的增加,能量实部的能隙逐渐减小。当λ处于λPT=1时,两个能带的实部在k=π处能隙关闭,并且复能量开始出现(图 1(b))。当λ>λPT时,如图 1(c)所示,即λ=1.05,部分能量的实部变为零,相应的能量虚部在零两侧对称出现。

Fig.2 Real parts and imaginary parts of (2)as a function of λ for different φ. (a) Δ=0.5,φ=0; (b) Δ=0.5,φ=π.图2 对于不同φ以λ为函数的和的实部和虚部。(a) Δ=0.5,φ=0;(b) Δ=0.5,φ=π

(4)

(5)

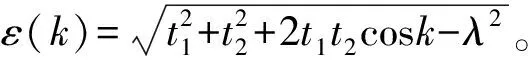
(6)

Fig.3 (a) Real part of the energy spectra under open boundary condition (OBC);(b) imaginary part of the energy spectra under OBC.(c),(e) and (g) show the real parts of the wave function labeled in (a) and (b).And (d), (f) and (h) are the imaginary parts for the corresponding states.(c), (d) show one of edge modes at φ=π marked by circle in (a) and (b).And (e), (f) are the other edge mode marked by rhombus. For both cases,the eigenfunction are located at the left or right boundaries at the lattice.However, the bulk state corresponding to (g), (h) with φ=π andenergy -1.064 6 is marked by triangle. Here,Δ=0.5,λ=0.4.图3 (a)在开边界条件下能谱的实部;(b)在开边界条件下能谱的虚部。(c),(e)和(g)展示了在(a),(b)中被标记出来的波函数的实部。(d),(f)和(h)是相应能态的虚部。(c),(d)展示了(a)和(b)中由圆环标记出的在φ=π处的边界模。(e),(f) 是另外一个由菱形标记出的边界模。这两种情况,本征波函数都局域在左或者右边界。然而对于由三角标记的在φ=π且能量为-1.064 6的体态被展示在(g),(h)中。这里Δ=0.5,λ=0.4

一般来说,在开边界条件下出现边界态是拓扑非平庸系统的特征。图3(a),(b) 展示了在开边界条件下以φ作为函数的能量的实部和虚部,取Δ=0.5,λ=0.4。边界模被发现处于π/2<φ<3π/2,它类似于λ=0的情况[35]。边界模的能量的实部为零,是二重简并的,而虚部的绝对值总是相等,符号相反。在区域0<φ<π/2和3π/2<φ<2π并没有边界模出现,这表明此区域为拓扑平庸的。在图3(a)和(b)中标记出来的特殊点的波函数的分布被展示在图 3(c)-(h)中,例如由圆环标记的在φ=π处的边界模被展示在图 3(c)和(d)中,另一个由菱形标记的被展示在图 3(e)和(f)。这两种情况下,波函数局域在左或者右边界。而在φ=π处能量为-1.064 6由三角形标记的体态被展示在图 3(g)和(h)。

-t1φn,2-t2φn-1,2+iλφn,1=Eφn,1,

-t2φn+1,1-t1φn,1-iλφn.2=Eφn,2,

(7)

由此我们可以获得转移方程为:

(8)

这里M(E)是一个2×2的转移矩阵,在开边界条件下,出现边界模的条件为M21(E)=0并且M11(E)M22(E)=1[36]。我们系统中的转移矩阵可以写为:

(9)

利用边界模条件,我们发现当|t1/t2|=|(1+Δcosφ)/(1-Δcosφ)|<1且能量E=iλ时,波函数φn,2=0并且φn,1=(-t1/t2)n-1φ1,1,表明是局域在左边界[见图 3(c)和(d)],然而对于|t1/t2|≥1,边界模不存在。同样得到当|t1/t2|>1,能量E=-iλ时边界模局域在右边界。

3 结论

我们研究了具有PT对称的SSH模型的拓扑性质,发现系统不具有宇称不变,时间反演不变却具有宇称和时间反演联合的对称性。尽管系统是非厄米的,但是PT对称的系统在某些参数区域能谱仍然为全实数。我们讨论了系统能谱的特性,在λ<λPT时,能谱为全实数,而λ>λPT时,能谱出现虚数。并且在PT对称性未破缺区域,利用类贝里相位作为拓扑数来区分系统的拓扑特性。在开边界条件下,在拓扑非平庸相,系统具有非平庸的边界模,而平庸相,则边界模消失。最后我们利用转移矩阵方法讨论了系统边界模的特性。通过研究发现在PT对称性未破缺区域,系统的拓扑特质和标准的SSH模型相类似。而对于PT对称性破缺的区域,其拓扑性质仍然需要继续研究。

参考文献：

[1] 张永德.量子力学(第三版)[M].北京:科学出版社,2017:16-22.

[2] Lee T,Wick G.Negative Metric and the Unitarity of the S-matrix[J].NuclearPhysicsB,1969,9(2):209-243.DOI:https:∥doi.org/10.1016/0550-3213(69)90098-4.

[3] Bender C M,Boettcher S.Real Spectra in Non-hermitianhamiltonians Having PT Symmetry[J].PhysRevLett,1998,80(24):5243-5246.DOI:https:∥doi.org/10.1103/PhysRevLett.80.5243.

[4] Brower R C,Furman M A,Moshe M.Critical Exponents for the Reggeon Quantum Spin Model[J].PhysicsLettersB,1978,76(2):213-219.DOI:https:∥doi.org/10.1016/0370-2693(78)90279-4.

[5] Denham S,Harms B,Jones S.Complex Energy Spectra in Reggeon Quantum Mechanics with Cubic Plus Generalized Quartic Interactions[J].NuclearPhysicsB,1981,188(1):155-175.DOI:https:∥doi.org/10.1016/0550-3213(81)90110-3.

[6] Andrianov A.The Large N Expansion as a Local Perturbation Theory[J].AnnalsofPhysics,1982,140(1):82-100.DOI:https:∥doi.org/10.1016/0003-4916(82)90336-0.

[7] Hollowood T.Solitons in Affine Toda Field Theories[J].NuclearPhysicsB,1992,384(3):523-540.DOI:https:∥doi.org/10.1016/0550-3213(92)90579-Z.

[8] Scholtz F,Geyer H,Hahne F.Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle[J].AnnalsofPhysics,1992,213(1):74-101.DOI:https:∥doi.org/10.1016/0003-4916(92)90284-S.

[9] Caliceti E,Graffi S,Maioli M.Perturbation Theory of Odd Anharmonic Oscillators[J].CommunicationsinMathematicalPhysics,1980,75(1):51-66.DOI:https:∥doi.org/10.1007/BF01962591.

[10] El-Ganainy R,Makris K G,Christodoulides D N,etal.Theory of Coupled Optical PT-symmetric Structures[J].OptLett,2007,32(17):2632-2634.DOI:https:∥doi.org/10.1364/OL.32.002632.

[11] Klaiman K,Günther U,Moiseyev N.Visualization of Branch Points in PT-symmetric Waveguides[J].PhysRevLett,2008,101(8):080402-4.DOI:https:∥doi.org/10.1103/PhysRevLett.101.080402.

[12] Makris K G,El-Ganainy R,Christodoulides D N,etal.Beam Dynamics in PT symmetric Optical Lattices[J].PhyRevLett,2008,100(10):103904-4.DOI:https:∥doi.org/10.1103/PhysRevLett.100.103904.

[13] Musslimani Z H,Makris K G,El-Ganainy R,etal.Optical Solitons in PT Periodic Potentials[J].PhysRevLett,2008,100(3):030402-4.DOI:https:∥doi.org/10.1103/PhysRevLett.100.030402.

[14] Longhi S.Bloch Oscillations in Complex Crystals with PT Symmetry[J].PhysRevLett,2009,103(12):123601-4.DOI:https:∥doi.org/10.1103/PhysRevLett.103.123601.

[15] Guo A,Salamo G J,DuchesneD,etal.Observation of PT-symmetry Breaking in Complex Optical Potentials[J].PhysRevLett,2009,103(9):093902-4.DOI:https:∥doi.org/10.1103/PhysRevLett.103.093902.

[16] Rüter C E,Makris K G,El-Ganainy R,etal.Observation of Parity-time Symmetry in Optics[J].NatPhys,2010,6:192-195.DOI:10.1038/NPHYS1515.

[17] Szameit A,Rechtsman M C,Bahat-Treidel O,etal.PT-symmetry in Honeycomb Photonic Lattices[J].PhysRevA,2011,84(2):021806-5.DOI:https:∥doi.org/10.1103/PhysRevA.84.021806.

[18] Longhi S.Convective and Absolute PT-symmetry Breaking in Tightbindinglattices[J].PhysRevA,2013,88(5):052102-12.DOI:https:∥doi.org/10.1103/PhysRevA.88.052102.

[19] Fleury R,Sounas D,Alù A.An Invisible Acoustic Sensor based on Parity-time Symmetry[J].NatCommun,2015,6:5905.DOI:10.1038/ncomms6905.

[20] Zhu X,Ramezani H,Shi C,etal.PT-symmetric Acoustics[J].PhysRevX,2014,4(3):031042-7.DOI:https:∥doi.org/10.1103/PhysRevX.4.031042.

[21] Lin Z,Schindler J,Ellis F M,etal.Experimental Observation of the Dual Behavior of PT-symmetric Scattering[J].PhysRevA,2012,85(5):050101(R)-4.DOI:https:∥doi.org/10.1103/PhysRevA.85.050101.

[22] Su W P,Schrieffer J R,Heeger A J.Solitons in Polyacetylene[J].PhysRevLett,1979,42(25):1698-1701.DOI:https:∥doi.org/10.1103/PhysRevLett.42.1698.

[23] Takayama H,Lin-Liu Y R,Maki K.Continuum Model for Solitons in Polyacetylene[J].PhysRevB,1980,21(6):2388-2393.DOI:https:∥doi.org/10.1103/PhysRevB.21.2388.

[24] Su W R,Schrieffer J R,Heeger A J.Soliton Excitations in Polyacetylene[J].PhysRevB,1980,22(4):2099-2111.DOI:https:∥doi.org/10.1103/PhysRevB.22.2099.

[25] Jackiw R,Rebbi C.Solitons with Fermion Number 1/2[J].PhysRevD,1976,13(12):3398-3409.DOI:https:∥doi.org/10.1103/PhysRevD.13.3398.

[26] Heeger A J,Kivelson S,Schrieffer J R,etal.Solitons in Conducting Polymers[J].RevModPhys,1988,60(3):781-850.DOI:https:∥doi.org/10.1103/RevModPhys.60.781.

[27] Ganeshan S,Sun K,Sarma S D.Topological Zero-energy Modes in Gapless Commensurate Aubry-André-Harper Models[J].PhysRevLett,2013,110(18):180403-5.DOI:https:∥doi.org/10.1103/PhysRevLett.110.180403.

[28] Li L,Xu Z,Chen S.Topological Phases of Generalized Su-Schrieffer-Heegermodels[J].PhysRevB,2014,89(8):085111-7.DOI:https:∥doi.org/10.1103/PhysRevB.89.085111.

[29] Ryu S,Hatsugai Y.Topological Origin of Zero-energy Edge States in Particle-hole Symmetric Systems[J].PhysRevLett,2002,89(7):077002-4.DOI:https:∥doi.org/10.1103/PhysRevLett.89.077002.

[30] Goldman N,Budich J C,Zoller P.Topological Quantum Matter with Ultracold Gases in Optical Lattices[J].NatPhys,2016,12:350-354.DOI:10.1038/nphys3803.

[31] Nakajima S,Tomita T,Taie S,etal.Topological Thouless Pumping of Ultracold Fermions[J].NatPhys,2016,12:296-300.DOI:10.1038/nphys3622.

[32] Meier E J,An F A,Gadway B.Observation of the Topological Soliton State in the Su—Schrieffer—Heegermodel[J].NatComm,2016,7:13986-6.DOI:10.1038/ncomms13986.

[33] Bender C M,Brody D C,Jones H F.Complex Extension of Quantum Mechanics[J].PhysRevLett,2002,89(27):270401-4.DOI:https:∥doi.org/10.1103/PhysRevLett.89.270401.

[34] Zhang X Z,Song Z.Geometric Phase and Phase Diagram for a Non-Hermitian Quantum XY Nodel[J].PhysRevA,2013,88(4):042108-5.DOI:https:∥doi.org/10.1103/PhysRevA.88.042108.

[35] Zhu B,Lü R,Chen S.PT Symmetry in the Non-Hermitian Su-Schrieffer-Heeger Model with Complex Boundary Potentials[J].PhysRevA,2014,89(6):062102-6.DOI:https:∥doi.org/10.1103/PhysRevA.89.062102.

[36] Bernevig B A,Hughes T L.Topological Insulators and Topological Superconductors[M].Princeton:Princeton University Press,2013.