天津市耀华中学(300040) 明廷军

立体几何是高中数学中的重点内容,由于立体图形往往要求以二维的形式呈现出三维的效果,这使得学生很难把握几何体中点、线、面之间的真实关系,所以立体几何成了学生高中学习中的难点内容.其实很多立体几何知识只是平面几何知识的延续与拓展,因此如何在二维平面的基础上进行观察、想象与分析,进而去化解三维空间中的问题,在我们的立体几何学习中显得尤为重要,本文尝试着从实例剖析的角度去引导学生对几何问题进行“降维”,培养学生的空间想象能力与逻辑推理能力.

一、在复杂结构中认识图形

立体图形中的结构往往比较复杂,对复杂结构的理解程度直接影响着我们的解题能力,所以认识图形、弄清结构是解决问题的关键.

例1长方体ABCD−A1B1C1D1中,AB=BC=1,,设点A关于直线BD1的对称点为P,则P与C1两点之间的距离为( )

解因为长方体ABCD−A1B1C1D1中,,所以,因为设点A关于直线BD1的对称点为P,所以在△AD1B 中,,所以即 ∠PD1C1=30°,因为在 △PD1C1中,D1C1=1,,所以根据余弦定理得出:,故选A.

图1

图2

二、在复杂结构中变换图形

在立体图形中,有些元素并不在同一个平面上,这给我们认识图形带来了很大困难,如果将其中一些平面进行翻折,让相关元素呈现在同一个平面中,这将方便我们认识图形,大大提升我们解决问题的能力.

例2如图3所示,在单位正方体ABCD−A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为( )

图3

图4

解如图4 所示, 把对角面旋转至使其与在同一平面上, 连接则为所求的最小值.故选D.

例3已知各棱长均为1的四面体ABCD中,E是AD的中点,P∈直线C E,则BP+DP的最小值为( )

解由于各棱长均为1的四面体是正四面体,把平面BEC及平面CED以CE为折线展平,三角形CED是正三角形的一半,,BC=1,故在平面DEBC中,连接BD,与EC相交于P点,则DP+BP为最短距离,在三角形BEC中,根据余弦定理,

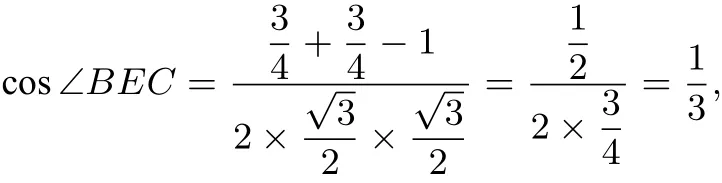
所以

图5

图6

例4过长方体A1B1C1D1−ABCD的对角线AC1的截面是平行四边形AMC1N,其中M ∈A1B1,N∈DC,AB=3,BC=1,C1C=2,当平行四边形AMC1N的周长最小时,异面直线MC1与AB所成的角为( ).

图7

解如图要使平行四边形AMC1N的周长最小,需将平面A1B1BA与平面A1B1C1D1展开,让AMC1在一条直线上即可,其展开图如图7.在正方形ABC1D1中,可得B1M=1,即B1M=1时平行四边形AMC1N的周长最小,因为AB//A1B1,所以∠C1MB1就是异面直线MC1与AB所成的角.在Rt△C1B1M 中,B1M=C1B1=1,所以∠C1MB1=45°,所以异面直线MC1与AB所成的角为45°.故答案为 45°.

三、在复杂图形中综合运用图形

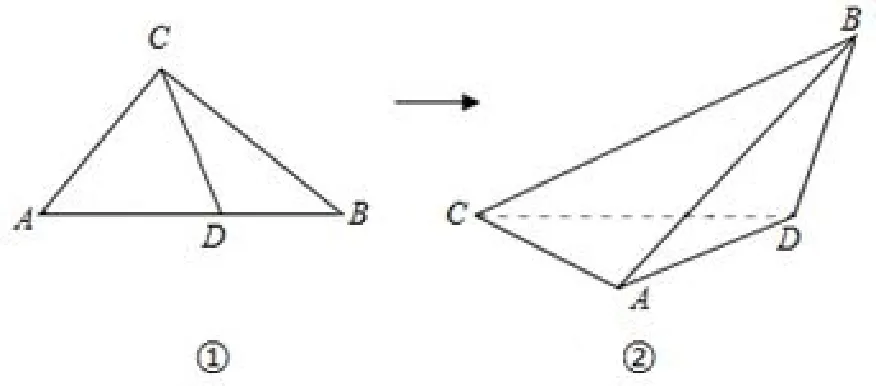
图8

在变换图形的过程中,有些元素是不变的,如果能从中发现图形的这些特点,合理运用图形,将复杂陌生的问题化作简单熟悉的问题,那么我们的能力一定会在图形的不断变换中得到培养,我们的思路也将得到开阔.

例5在Rt△ABC中,已知D是斜边AB上任意一点(如图8①),沿直线CD将△ABC折成直二面角B−CD−A(如图8②).若折叠后A,B两点间的距离为d,则下列说法正确的是( )

A. 当CD为Rt△ABC的中线时,d取得最小值

B. 当CD为Rt△ABC的角平分线时,d取得最小值

C. 当CD为Rt△ABC的高线时,d取得最小值

D. 当CD为Rt△ABC的边上移动时,d为定值

解如图,

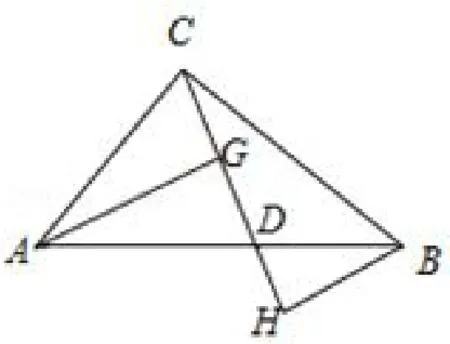
图9

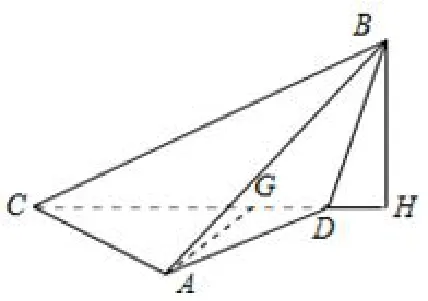
图10

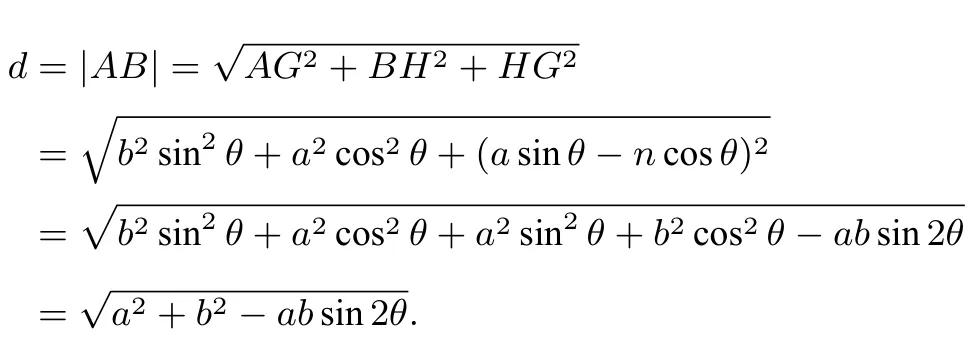
在立体几何的学习过程中,一定要努力研究图形的结构,把空间中两个或两个以上的平面联系起来,转化成一个新的平面,搭出新图形的框架,进而扩展学生的探究思维,提高学生的判断力,养成学生的空间想象能力,为后续的几何学习打下坚实的基础.

我们也可以看到,正是因为有了几何图形的变换,才有了几何的魅力,在立体几何的学习过程中,如果能正确地认识图形,不断地变换图形,我们一定可以将我们的学习提升到一个新的高度.