☉广东省广州市番禺区石楼中学 刘新萍

教会学生在解题中怎样探寻解题突破与思路是值得广大高中数学教师尤为重视的课题.有些教师面对课堂教学中的例题往往会直接进行求解，这样的做法往往会令学生的思维形成定式且不能拓展.本文结合解题指导的顺序与实际案例对解题应有的策略进行了大概的分析.

一、引导学生“先估后算”

面对实际问题首先进行粗略估计是解题中的第一步，这一“初步定向”的审题步骤主要锻炼的是学生面对问题时的洞察力.比如，在已知直角三角形中的两个独立条件的情况下进行问题的求解，往往利用勾股定理与三角比知识就可以解决问题，而条件不够、问题又不确定时就应该采用方程来解决了.

先估后算一般包含条件与数量这两方面的估计.

1.条件的估计

条件的估计包含条件是否多余或缺少、是否存在矛盾、是否可变等主要的内容.

例1 如图1，已知△ABC中，AM是BC上的中线，CN⊥AM，BC=2，沿AM将△CAN翻折到△AND，说出BD与BC数量关系.

部分学生思路如下：MN是△BCD的中位线，所以比较MN和MC即可比较出BD和BC，且AM⊥CD，所以斜边MC＞MN，即BC＞BD，但参考答案却是BC=BD.于是他想证明∠CBD=45°，但最终没能证明.

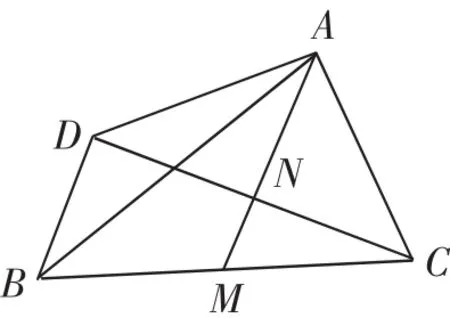
图1

事实上，想证明∠CBD=45°，就是证明∠CMN=45°，这是中线AM与BC的夹角，题中并没有谈及它等于45°，虽然进行了一定的翻转等操作，但它不会变成45°.

因此，基本量不足的情况下问题是可变的.

2.数量的估计

基本量不足导致问题可变时就应该首先搞清楚问题中究竟有哪些量，然后再去分析固定的量、变的量、初始量、会跟着变的量、这些量的变化范围等等.

例2 用50米的材料围成一饲养场并使其面积最大，应该怎样围？

有些学生解题如图2所示，设宽为x，列式y=x（50-2x），然后求函数最大值.

学生在此类题目刚刚出现时就接触列函数式的解法往往不能适应，教师应这样分析：

当宽x=1米，长为50-2x=48米，面积为S=1×48=48平方米；

当宽x=2米，长为50-2x=46米，面积为S=2×46=92平方米；

……

学生在教师的推理分析中很快能够明白S是随着x的变化而变化的.教师如果能够经常引导学生对这方面进行关注，学生在长久的训练中就会逐步养成分析变量、常量的习惯，理解题意时的效果就会更好.

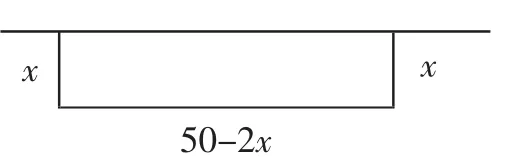
图2

二、引导学生模式识别，探求优法

教师引导学生在初步估计之后进行解题的思考便是模式识别这一步骤了，学生一旦能够领略并使用模式识别的策略，常规题的解决将会取得尤为欣喜的效率与效果.做过的范例以及自己归纳的解题模式等等都属于解题的一些模式.教师在解题教学时应帮助学生理解其中蕴含的思想方法这一模式的灵魂，帮助学生正确掌握解题的步骤，避免乱套无用模式，使得学生在常规题的解决中做到快速而准确.如数列是高考中的重点内容，解决这些相关问题时，主要思路：1.联立方程组（或不等式组），通过解方程组（或不等式组）来求解；2.选择恰当的变量建立目标函数，再用函数的知识来解决问题.

例3 等比数列{an}中，S2=2，S4=8，则S6=（ ）.

A.-32 B.32 C.-26 D.26

等比数列中有五个量a1，n，q，an，Sn，一般可以“知三求二”，通过列方程（组）求关键量a1和q，问题可迎刃而解.

掌握通法之后还应该对优法进行一定的探求，本题还可以利用等比数列的性质来求解，教师在解题教学时应帮助学生逐步锻炼出一眼看穿问题本质的能力并投入应用中，注重数学思想方法的培养对于学生解题能力的培养很有意义.

解析：因为S2，S4-S2，S6-S4成等比数列，

所以（S4-S2）2=S2（S6-S4），

所以36=2（S6-8），S6=26.

有些具体问题虽然由几个内容组成，但解题时有意放大视角并将研究对象看成为一个整体来使问题得以求解即是这里所指的整体思维.研究问题的形式、结构以及处理得到整体视角的分析往往能令解题变得更加简洁而顺利，教师在平日的教学中也应有意识地培养学生整体思维的意识与习惯.例4 5a2+25a+9=0，9b2+25b+5=0，求.

从问题呈现的整体形式看，学生通过观察可知，两式子系数对称，将9b2+25b+1=0两端除以b2，得5 （）2+25）+9=0，可知a和是方程5x2+25x+9=0的两根，利用韦达定理可知，.

对于内部构造与机理不能直接观察的事物或系统在系统科学的范畴里被称为黑箱，而那些部分机理还是明确的则称为灰箱.黑箱原理的基本思想在于借助外部考察输入黑箱与其输出反馈信息之间的变化关系来探求问题结果，中学数学中的问题大多为已知部分机理的“灰箱”.

三、引导学生多元化分析条件结论

如果通法、优法尤其是“一眼看穿”的方法在某问题的解决中都行不通，这时候只好对题中的条件、结论等进行仔细的分析了，这就是本文所要讨论的双向分析与差异分析等策略了.

1.双向分析策略

双向分析就是指把已知条件及其伸展、结论的倒溯这两个方面结合起来进行分析并最终找到解题的中间环节而获求解的方法.

简单说来，就是借助条件A进行正面、顺向的思考并得到经过一定理解或转化的条件B1，B2，B3，…；然后再从结论D出发寻找此结论生成必须依赖的命题C1，C2，C3……

如果由B1，B2，B3，…中的某个Bi可以推出C1，C2，C3，…中的某个Ci，则可得到一串命题：A-Bi-Ci-D，则命题得证.

双向分析的运用中有时只要用到追溯，有时只要用到条件伸展就能够解决问题，因此，教师引导学生进行双向分析时不能机械运用.

2.差异分析

条件与结论之间的逻辑关系是双向分析时所侧重的要点，而条件与结论之间的差异则是差异分析法尤其注重的关键.

例6 若a、b、c是互不相等的实数，且满足关系式

b2+c2=2a2+16a+14， ①

bc=a2-4a-5， ②

则a的取值范围为______.

条件是关于a、b、c的两个等式，要求的则是关于a的不等式，对比分析可知其差异性表现在以下三个方面：

（1）条件中包含两个式子，但要求的只是一个，因此立马可以联想合并条件；

（2）条件中涉及了三个字母，但要求的只是一个，因此立马可以联想消元；

（3）条件中给出的式子是等式，但要求的却是一个不等式，因此立马可以联想到对等式放缩.

解：①-2×②，（b-c）2=24a+24，因b≠c，有（b-c）2＞0，则24a+24＞0，a＞-1.

四、变更问题引导学生再思考

如果对条件与结论进行如此的分析之后还不能求解，那么解题者就应该要考虑到变更问题才行了.变更问题时可以将问题全部变更，也可以将条件或者结论进行单独的变更.

1.表示形式的转换

学生对某些问题的表示形式难以理解或难以探究出解题思路时，教师应该适时引导学生将其表示形式作出一定的变换，问题很可能迎刃而解.如求函数的零点个数问题，有部分复杂的方程学生是无法解出的，要将函数变为两个简单函数，画出它们的图像交点的个数就是零点的个数，初学的学生比较难解决这类数形结合的问题，老师在教学过程中不断渗透.

例7函数f（x）=lnx+x-2的零点个数为______.

解法：作出函数g（x）=lnx，h（x）=-x+2图像，由图3可知f（x）的零点个数为1个.

2.问题转化

如果转化为|AB|是x的函数，则此题就由几何问题转化成了代数问题.

3.逻辑转换

数学解题中可以通过原命题的逆命题或否命题的研究并将之与原命题的本质进行联系来解决问题.

例8 已知以下二次方程：x2+4mx+4m2+2m+3=0；x2+（2m+1）x+m2=0；（m-1）x2+2mx+m-1=0. 其中至少有一个方程有实根，则m的取值范围为（ ）.

当然在变式的过程中运用的最多的是分类讨论思想，当问题比较复杂甚至难以入手时，一般将其转化成比较简单且易于解答的一道或几道新题.

上面一些常用方法，老师在平时的教学中，可经常渗透，让学生有一个接受，消化的过程，让他们建立起解题的一套方法和思路，但重要经验是优化基础，把知识结构化、系统化、程序化，在优化的基础上，适当地做一些新题.基础好了，才能够做到解题活，才能综合知识，有较快的解题速度，所以应该把主要精力放在优化解题过程，浓缩提炼知识的机构，优化解题方法.H