☉江苏省常熟市浒浦高级中学 张芝悦

数学概念一直是数学教学的重中之重，但又是常态课教学较为轻松的地方.笔者以为，常态课教学中教师对于概念教学往往不肯花费过多的时间，导致学生在概念的理解和运用上往往捉襟见肘，这与当下课程教学课时紧有一定的关系；另一方面，教师注重的是学生的应试成绩，往往对学生数学素养的关心少之又少，这也导致了教师宁可多研究解题方法、教学生解题模式，也不愿在概念上多下工夫，毕竟概念教学对于数学的理解和素养的提高，在应试中是难以量化呈现的.

种种与课程标准相违背的教学方式，导致了今天的概念教学失去了概念教学的本质.学生对于概念的理解基本只能依赖数学试题，教师离开试题谈对概念的理解也几乎是哑口无言.章建跃博士在强调概念教学时，多次提及不惜时、不惜力.因此笔者以本课为例，谈一谈教学的深刻性.

《曲线和方程》是解析几何的起始课，为什么这一节内容深藏于此？我们思考过吗？为什么不放在圆的前面？笔者以为：往前思考，初中数学对于圆的研究主要是一种定性，定性的含义指的就是偏向几何直观，而数学越往高纬度发展，其必须从定性向定量做华丽的转身.吴文俊先生所说的“数学高纬度中除了机械化的运算，我实在想不出更好的方式”，暗指了代数机械化的魅力！从定量的研究圆，到椭圆、双曲线和抛物线的介入，从而实现了对“点”的理解需要更多地向定量靠拢，因此本节出现在定性的圆和定量的椭圆之间，呈现了承接的作用.这种靠拢促成了“曲线和方程”的关键地位，但是对于这一概念的教学需要从几何性中的“点”出发，逐步逐层次地深入挖掘.

问题1：椭圆中心在原点，一个焦点是F（-1，0），求这一类椭圆中与直线l：2x-y+3=0有公共点且离心率最大的椭圆标准方程.

分析：本题可以从两个不同的视角切入，是典型的解析几何双重特性问题.

视角1：利用代数视角，学生不难发现，解决离心率最大值即求解椭圆方程（a＞b＞0）中a的最小值，考虑到直线l：2x-y+3=0与椭圆1（a＞b＞0）有公共点，从而利用判别式求解的取值范围，进而求解本题，从这一视角来说，学生基本能清楚地获得分析过程.

视角2：学生通过运算发现，代数解法对于学生而言最大的困扰是运算量稍大，而且未能体现椭圆最本质的知识，引导学生思考：你觉得上述方式困难的原因是什么？——代数运算复杂——既然代数运算复杂，说明代数化有些烦琐，那你可以从哪个角度换一种切入？——几何！——与2a有关的几何特征是什么？——焦点三角形及椭圆定义——两段和最小以图形结构思考如何实现？——点关于线的对称——三点共线.因此记右焦点Q（1，0），本题只要解决F（-1，0）关于直线l：2x-y+3=0的对称点P，从而最小的2a=|PQ|.

设计意图：从代数和几何的双视角寻求问题的解决，是曲线上“点”满足方程的解的一大特征，但是我们不难发现，深化这一概念的理解，从代数上理解了第一层面，即曲线上的点是方程的解，从几何上理解了第二层面，即曲线上的点需要满足曲线定义.

问题2：圆的方程x2+y2=10，若弦BC的中点D求该弦所在直线方程.

分析：引入问题2，继续从代数几何双重性中寻求问题的解决.

视角1：圆中的问题更偏向几何手段，即以垂径定理为依据的弦心距三角形的处理，本题自然水到渠成.

视角2：代数视角更具备了一般性，即圆、椭圆、双曲线等等，都具备点在曲线上的妙用，而这种妙用依赖的代数方式主要是“点差法”.

变式：椭圆方程2x2+y2=1，若弦BC的中点求该弦所在直线方程.

分析：经过学生思考，发现几何方式在这里有一定的困难，而点差法却具备了普适性.

设计意图：通过问题2和变式，让学生理解曲线上点运用方式需要关注曲线的形态，进一步理解曲线上点的运用方式.

问题3： 求椭圆2x2+y2=1上的点到直线y=x-4的距离的最值.

分析：进一步思考曲线上点的运用方式，考虑到研究距离最值，从双重视角入手分析.

视角1：点在曲线上，若直接利用点到直线的距离公式，进一步的计算稍显难度，但是考虑到曲线上点满足方程，我们可以从点的形态继续思考，这里显然三角换元之后的点形态运用，令利用点到直线的距离公式结合三角知识可求得.

视角2：从几何直观来说，学生很容易想到相切位置的最值存在，因此利用判别式求解即可.

设计意图：本题的设计，主要是引导学生思考曲线上点运用的多样化，可以是原生坐标形态，也可以是三角坐标等等，学习中要注意不同方式的转化.

问题4：设F1，F2分别为椭圆+y2=1的左、右焦点（如图1），点A，B在椭圆上，若，则点A的坐标是____________.

图1

图2

分析：作为2011年的浙江卷压轴填空题，我们不难发现本题对于点的运用方式提出了新的要求，学生初次研究都是设直线AF1的斜率为k（k＞0），则直线AF1的方程为y=k（x+），联立椭圆x2+3y2=3，整理得（1+3k2）x2+6k2x+6k2-3=0.但是发现该方程所表示的两根并不是点A，B的横坐标，因此陷入问题解决的困境.试想：韦达定理——出现无用的点——思考到椭圆的对称性（如图2），从而获得几何特征.

视角1：设直线AF1与椭圆的另一个交点为B1，设点A的坐标为（x，y），点B的坐标为（x，y）.由及椭11122圆对称性，可得|F1A|=5|F1B1|，得y1=-5y2.设直线AF1为x=ty-，联立椭圆+y2=1，得（t2+3）y2-2ty-1=0.

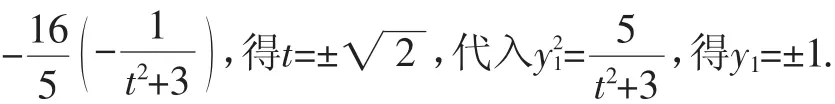
故点A的坐标是（0，±1）.

视角2：考虑到点在曲线上，也可以理解为方程的解.设点A，B的坐标为（x1，y1），（x2，y2），得

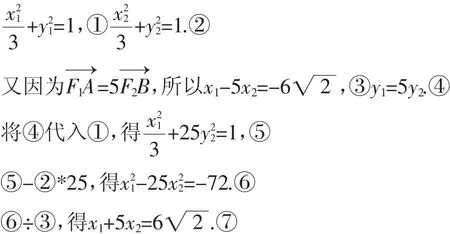
设计意图：以高考真题思考，曲线上点运用方式，满足曲线的几何性质，借助曲线形状获得较好的解决途径.

纵观本课的设计，笔者认为出现了概念教学的新境界和新层次，将教材中的《曲线和方程》的概念进行了深化、挖掘，获得了知识理解的深刻性.其亮点主要在于：《曲线和方程》一节只有一个概念，这个概念是一句充要条件的话，描述的是代数方程的解和几何曲线的点之间的等价性.我们可以回想自己在这里的教学：每一届学生，在这里基本都是一笑置之，因为觉得这一概念是一句“废话”，毫无价值的概念.学生的行为，可以理解，但是对于教师自身而言，尊重和理解数学概念更需要多一份深思熟虑，章建跃博士在《中小学数学》编后漫笔中多次谈及当下中学数学教学的概念教学：不少教师除了解题实在不会教学.而本课做到了有层次的概念认知，主要是两点：其一，中学数学是初等数学，纵观教学，几何方式往往更占据问题解决的主导位置，从而“点”是这一概念的核心.对于“点”如何运用的方式，体现了教学设计的层次性：点满足曲线定义——点运用需要考虑曲线形态——点处理借助曲线几何性质，螺旋上升；其二，华罗庚先生说读书是从“薄”——“厚”——“薄”的过程，对于这样的概念处理，做到了单一概念的发散、理解、深思，达到了鸟鸣山更幽的境地.

1.张奠宙.中国数学双基教学理论框架.数学教育学报［J］.2006（8）.

2.沈恒.千里之行，始于足下.数学教学［J］.2011（2）.

3.沈恒.谈如何提高学生的解题能力.中学数学研究［J］.2009（10）.H