王天一,刘 浩,黄 卓

(1.对外经济贸易大学金融学院,北京100029；2.北京大学国家发展研究院,北京100871)

1 引 言

资产收益的波动率在资产定价,风险管理,资产配置等领域占有重要地位.由于波动率本身有很强的时变性,其建模和预测问题一直是金融计量领域的核心问题之一.自ARCH和GARCH模型以来[1,2],有大量文献开始对其进行研究,并拓展出适应诸如杠杆效应,厚尾以及长记忆等收益率和波动率的常见特征的GARCH类模型[3].随着资产价格高频数据获取难度的降低,利用高频数据估计波动率的研究开始大量出现.其中,传统的GARCH模型和新出现的已实现测度如何结合成为一个研究热点.Engle等[4],Shephard等[5],Hansen等[6]的研究分别提出了三种不同的利用已实现测度对收益率和波动率进行联合建模的方法.这三类方法中,以已实现GARCH模型的结构最为简洁.实证结果表明,已实现GARCH模型在波动率预测方面可以显著地超越传统的GARCH模型[6].

文献中对已实现GARCH模型进行的研究主要有分布拓展和模型结构拓展等方面.分布拓展方面,Watanabe[7]研究了有偏分布的已实现GARCH模型对于SP500指数的在险价值和预期损失的预测能力.模型结构拓展方面,Hansen等[8]提出了能够引入多个已实现测度的已实现E GARCH模型,该模型能够更加灵活地对收益率和波动率之间的关系进行建模.Lunde等[9]对比了已实现E GARCH模型同EGARCH模型在预测NOMXC远期合约波动率上的表现.国内相关研究也已经起步(如文献[10—12]).

相比之下,既有研究对已实现GARCH模型在长记忆性建模方面的讨论相当缺乏.所谓长记忆性,是指波动率序列的自相关系数下降缓慢,显示出很强的持续性[13].实证研究表明,波动率的长记忆性对于其在多步预测[14],衍生品定价[15],风险管理[16]等问题上的表现有关键性的影响.国内亦有针对股票市场和期货市场长记忆性的研究[17,18].然而,已实现GARCH模型的约简形式比较简单,对波动率相关性的刻画存在限制.以文献中最常用的已实现GARCH(1,1)模型为例,其针对条件方差的约简形式基本上是ARMA(1,1)结构,而该结构本身并不能产生足够的记忆性.本文的实证结果指出,已实现GARCH模型参数隐含的“条件方差的理论自相关函数”与模型估计出来的“条件方差的样本自相关函数”之间有巨大的差异,说明在建模长记忆性上现有模型设定存在不足,有必要讨论如何改进.

现有的关于波动率长记忆性的模型基本上分成两大类:一类是GARCH类模型中的基于分数阶差分的FIGARCH模型[19],基于长短期成分建模的成分GARCH模型[20]等.另一类是直接使用已实现测度,忽略GARCH结构的ARFIMA模型[21],基于混频数据抽样的MIDAS模型[22],基于波动率瀑布效应(volatility cascade)的异质性自回归模型(HAR)模型[23]等.国内也有相关文献对这两类模型进行研究(如文献[24,25]等).

已实现GARCH模型作为GARCH族模型中的一员,最直接的提升记忆性的办法就是引入FI GARCH或者成分GARCH结构.但FI GARCH结构估计过程复杂,数据需求量大,经济意义不明显[23].成分GARCH模型的长短期效应并不能直接被观测,不容易在已实现测度的层面找到对应的可观测量.相比之下,引入混频数据抽样结构改进已实现GARCH模型是一种更为有效的方法.首先,混频数据抽样结构使用的是一个已实现测度的多期历史数据,而不是多个已实现测度的历史数据,因此改进后的已实现GARCH模型并不需要多个测量方程,模型结构简单,经济意义清晰.其次,混频数据抽样结构作为一种参数节约的设定,使用少量形状参数配合权重函数就可以给出对历史较长时间内已实现测度的加权系数.由于权重函数形式较HAR模型更加灵活,且形状参数本身也是待优化系数之一,这种方式可以有效地抽取数据中的长期波动信息.而这一成分是对传统已实现GARCH模型短期波动成分的重要补充.

基于以上观察,本文将混频数据抽样结构引入已实现GARCH模型中,构造出同时包含长短期已实现测度信息,能对波动率长记忆性进行建模的已实现混频数据抽样GARCH模型.对于指数和个股的实证结果表明,相比于已实现GARCH模型,新模型能够:1)显著提升模型拟合优度以及对波动率长记忆性的捕捉能力；2)显著提升波动率多步预测的精度.

2 已实现混频数据抽样GARCH模型

令rt表示资产在t期的收益率,xt表示t期已实现测度,ht表示rt的条件方差,Hansen等[6]提出的已实现GARCH模型可以写成如下形式

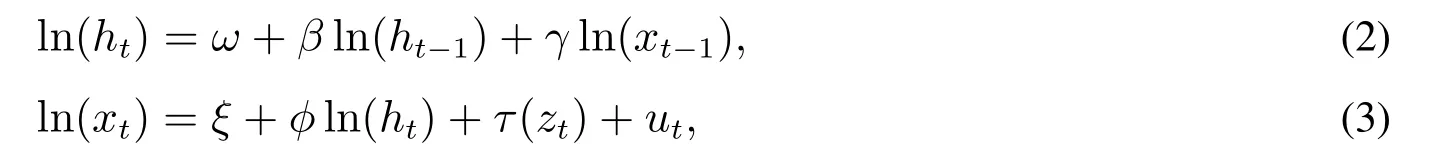
其中zt～N(0,1),,两者独立.

式(1)和式(2)分别对应传统GARCH模型中的均值方程和方差方程,式(2)中的波动率更新项由传统的“收益率平方”改成了信息更为丰富和准确的“已实现测度”.已实现GARCH关键特点是在均值方程和方差方程外,加入了“测量方程”(式(3)).其主要作用是连接已实现测度和条件方差,从而实现对收益率和已实现测度的联合建模.

相比GARCH—X模型,已实现GARCH模型可以实现波动率的多步预测.一般称τ(zt)为杠杆函数,用来刻画金融市场中普遍存在的收益率与波动率的非对称关系,

Ghysels等[22]提出的混频数据抽样方法可以利用较少的参数来赋权历史信息,基于前K期的已实现测度预测本期的已实现测度的混频数据抽样回归如下

其中ψk(ω1)为各期已实现测度的赋权函数,其设定依赖于具体的抽样方法.

在波动率建模和预测的文献中常用的函数形式有指数型函数,Beta型函数等.本文使用21阶单参数Beta函数来对数据进行赋权1虽然双参数Beta函数有更丰富的函数结构,但其参数估计稳定性较差,而且实证结果上与单参数Beta函数几乎没有差别,因此采用单参数Beta函数进行建模.,其具体形式如下

向方差方程式(2)中加入经过ψk(ω1)赋权的长期波动信息后,已实现GARCH模型的方差方程式变为

该模型称为已实现混频数据抽样GARCH模型.

与传统的已实现GARCH模型相比,新模型引入了过去22天(约合一个月的交易时间)的已实现测度信息,并且这种引入不以大量增加模型参数为代价.由于只使用了一个已实现测度,测量方程(3)不需要做任何调整.权重函数的定义保证各阶滞后项权重和为1,因此模型的稳定性条件为

将测量方程(3)代入方差方程(6)可得

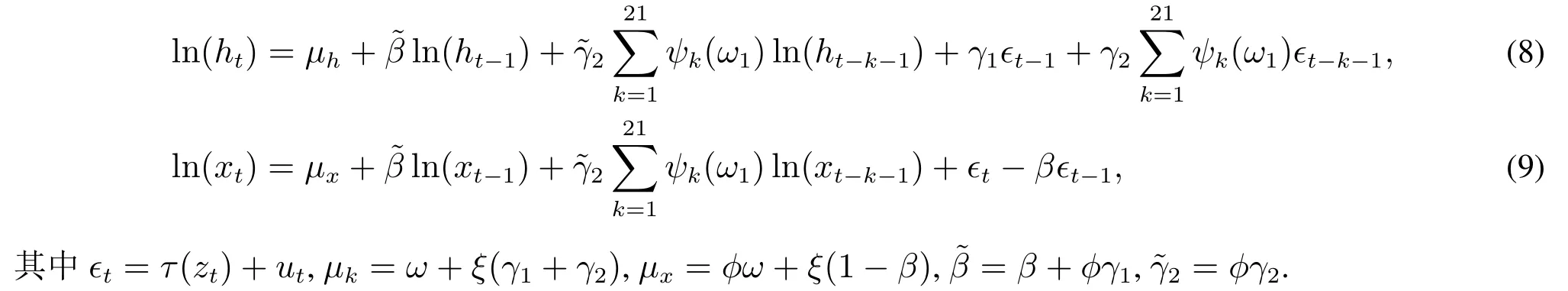
式(8)表明对数波动率服从带参数约束的类ARMA(22,22)结构,式(9)表明对数已实现测度服从带参数约束的ARMA(22,1)结构.这个结果说明在描述以实现测度动态的问题上,已实现混频数据抽样GARCH模型和传统的混频数据抽样回归本质上不一样2相同滞后阶的混频数据抽样回归实际上对应的是已实现测度的带参数约束的AR(22)模型..在后文实证部分可以看到,得益于上述更加丰富的结构,新模型相比已实现GARCH模型可以更好地描述ln(ht)和ln(xt)的动态.

由于加入混频数据抽样项并没有改变误差项(z,u)可以观测的事实,已实现混频数据抽样GARCH模型仍然可以沿用最大似然估计法(MLE)进行估计[6].在(z,u)相互独立的假设下,联合似然函数l(r,x)可以分成两部分:对应收益率残差z的部分记为l(r)；对应已实现测度残差u的部分记为l(x|r),即

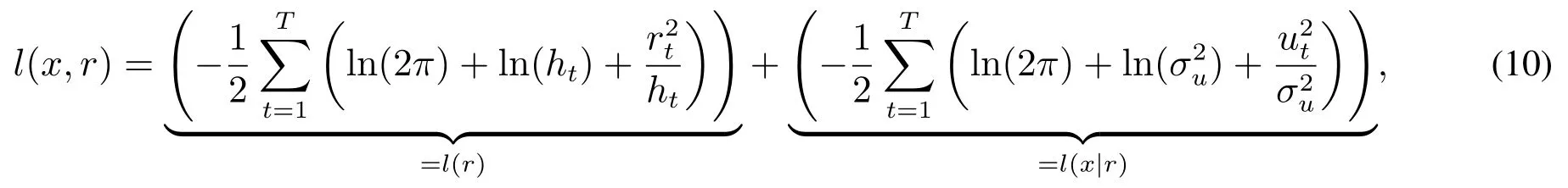
其中l(r)部分在后文中被称为半似然函数,可以显示出模型对于收益率分布拟合的情况.初始条件波动率h0作为参数一并进行估计.

3 实证结果

3.1 数 据

本文使用的数据包括五只个股(IBM,INTC,MSFT,WMT,XOM)以及SP500指数ETF(SPY)的日度数据3其中SPY是对应SP500指数的ETF,对整个市场有代表性.XOM为成分股中的大市值股票.IBM为成分股中的大权重股票.INTC,MSFT属于科技类股票.WMT代表的零售业相对周期性较弱.,时间跨度为2002—01—02～2013—12—31.收益率为使用对数收益率计算的“收盘价—收盘价”收益率4作者同样试验过基于“开盘价-开盘价”收益率和5 min已实现方差(RV)的实证结果,结果并无明显差异.,数据来源为Yahoo Finance网站.已实现测度采用已实现核估计(realized kernel,RK)进行估计[26],数据由Asger Lunde提供.其计算方法如下

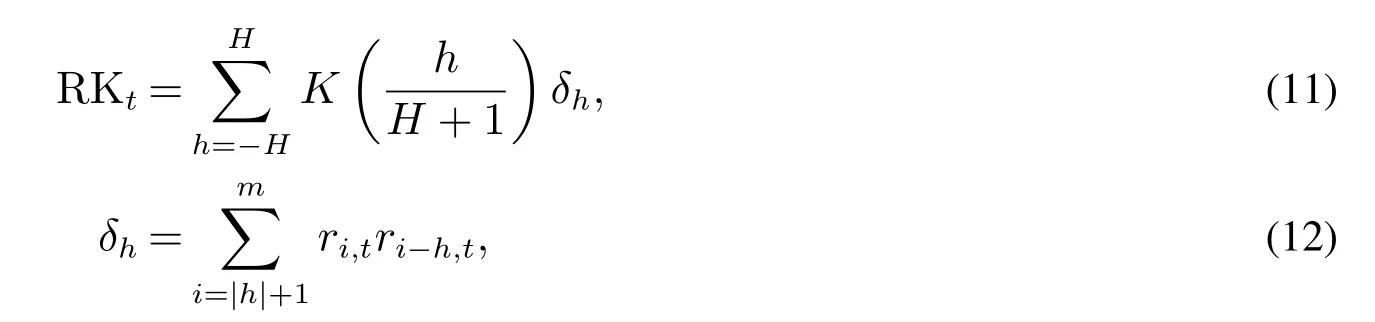
其中K(·)是核函数,H是核函数的带宽,m是每天取样的个数,ri,t是第t日的第i个日内收益率.

由于显式地考虑了日内收益之间的相关性问题,RK对于高频数据中存在的市场微观噪音有很强的免疫能力.表1给出了本文使用数据的描述性统计量5收益率的单位为百分之一,已实现测度亦做相应的调整..其中SPY,INTC和XOM呈现负偏度,其余呈现正偏度,超额峰度均大于0,说明各个序列均有一定的厚尾现象.

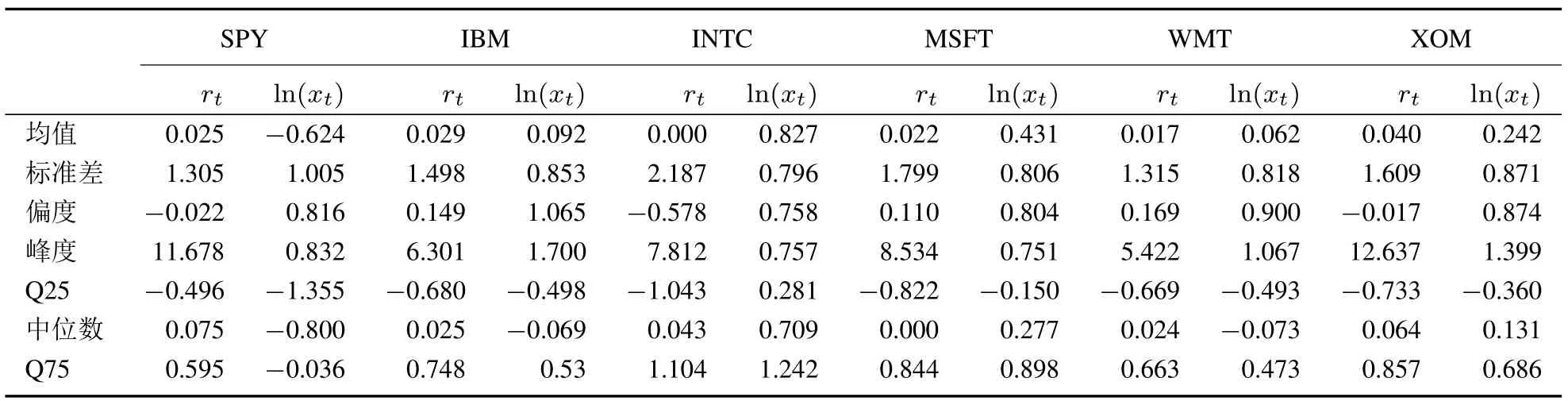
表1 描述性统计Table 1 Descriptive statistics

3.2 样本内估计结果

表2给出了已实现混频数据抽样GARCH模型的全样本估计结果,括号中是稳健性标准误.为了进行对比,对应已实现GARCH模型的全样本估计结果一并给出.下文为简洁起见,将已实现GARCH模型记为RG,已实现混频数据抽样GARCH模型记为RMG.

从表2中可以看出,相比于RG模型,RMG模型β系数的数值显著减小.这说明加入长期波动信息以后,条件方差一阶滞后项蕴含的长期波动信息被混合数据抽样项提供的信息替代了,因此其重要性相对下降.相比之下γ1变化不大,说明以滞后一期已实现测度衡量的短期信息并没有受到显著的影响.测量方程中系数ϕ的数值集中在1附近,说明对数RK(ln(xt))可以近似作为对数条件波动率(ln(ht))的一个无偏估计量6由于本文使用的是日间收益率,因此估计得到的条件波动率为日间波动率.因其包含了隔夜收益率变化,理论上该条件波动率会比已实现核测度更大一点..另外τ1＜0,τ2＞0说明全部序列都存在显著的杠杆效应.RG模型的β+γϕ以及RMG模型的的数值均接近于1,说明对数条件波动率以及对数已实现核估计都具有很强的持续性.半似然函数取值方面,RMG显著大于RG,说明加入长期波动信息使得标准化收益率更接近正态分布的状况.

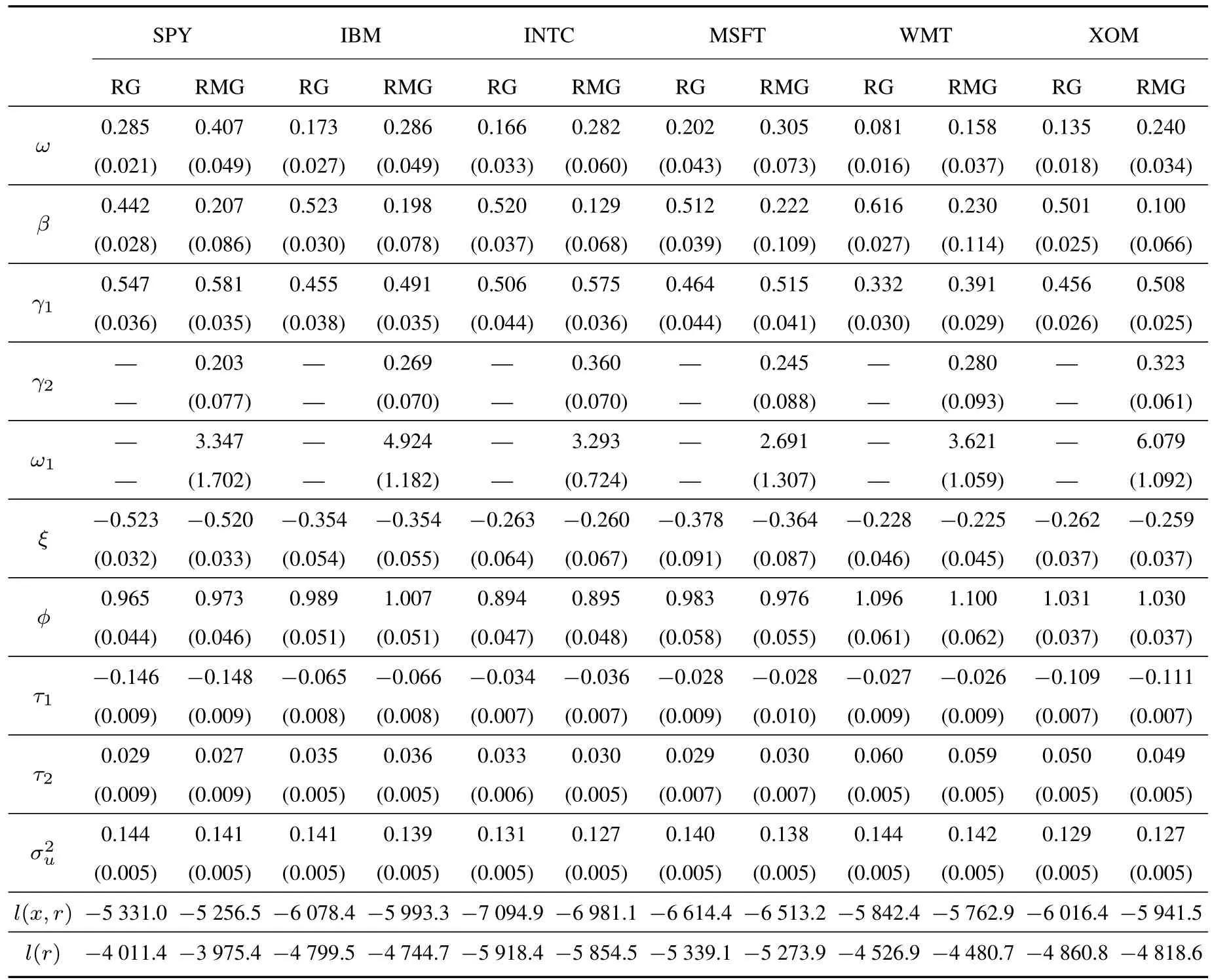
表 2 全样本参数估计结果Table 2 Full sample parameter estimates

借助全样本估计结果,可以计算各个序列对应的单参数Beta函数权重.如图1所示,不同模型的权重分布虽然都呈现下降的趋势,但是其下降速度和形状各不相同.这说明ψk(ω1)虽然只有一个参数,但是其能体现的权重形式并不单一.

由于RG模型内嵌于RMG模型,因此长期波动信息的显著性检验可以直接借助表2中汇报的似然函数值进行计算.具体的,针对“长期波动信息对波动率估计没有贡献”的零假设γ2=0,构造如下统计量

表3 对数似然函数值以及似然比检验结果Table 3 Log-likelihood and the results of likelihood ratio test

3.3 波动率的长记忆性

波动率长记忆性的一个表现就是波动率的自相关函数(ACF)下降速度缓慢.图2给出了不同模型拟合的对数条件方差的ACF(实线)与模型估计系数下计算的理论ACF(虚线)之间的比较7理论ACF的计算方式基于式(8)和式(9),使用ARMA模型ACF计算公式计算.对于lnh而言,由于其没有当期冲击,计算公式做了相应调整.为节约空间这里仅给出指数ETF序列SPY的结果,其他序列的结果类似,如需要可向作者索取..左边的图对应RG模型,右边的图对应RMG模型.如果模型有较好的内部一致性,两条ACF曲线的差距应该较小.从结果中可以看出,RG模型系数隐含的ACF显著地偏离了其条件方差拟合值的ACF.相比之下,RMG模型对RG模型有明显的改善,模型系数隐含的ACF序列下降速度的比RG对应序列慢,而且和模型条件方差拟合值的ACF更接近.

图1 全样本估计的混合频率抽样项权重图Fig.1 Full sample MIDAS weights

图3给出了模型系数隐含的对数已实现测度的ACF(虚线)与真实对数已实现测度ACF(实线)之间的比较.其中短点虚线对应RMG模型,长点虚线对应RG模型.如果模型隐含的ACF能贴近真实的ACF,模型捕捉长记忆性的能力就更强.从结果上看,RMG模型至少可以拟合20期的真实ACF,而RG模型在10期左右就开始出现偏差了.

3.4 样本外预测比较

测量方程的引入使得已实现混频数据抽样GARCH能够进行多步预测.为了表述的方便,令t=ln(ht),t=ln(xt).将方差方程代入到测量方程中,可以得到如下等式

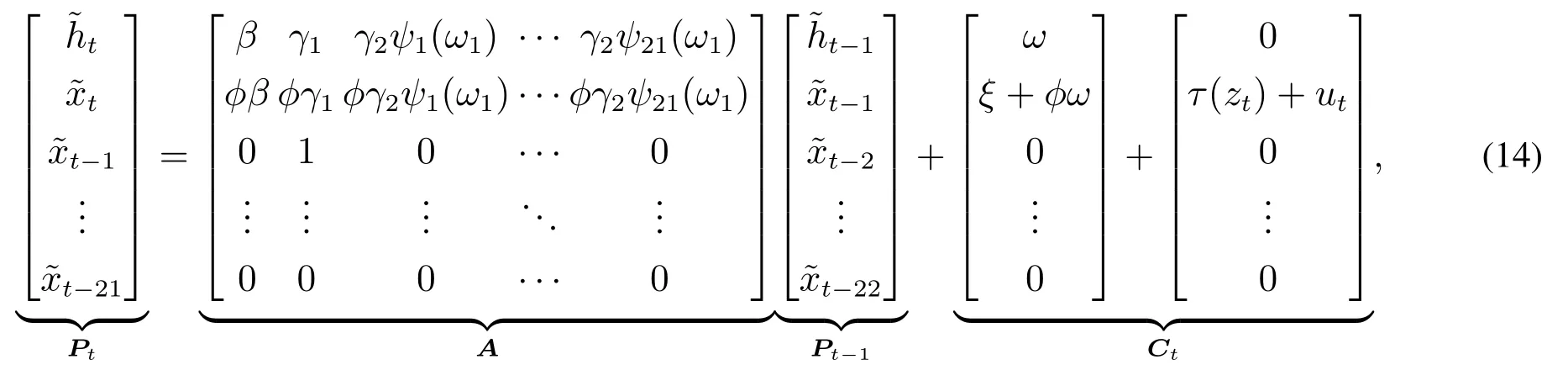
即Pt=APt-1+Ct,对应已实现GARCH模型的类似结构可以参见Hansen等[6].Pt的k步的预测为

条件方差ht的一步预测直接使用式(6)就可以获得,多步预测相对复杂.由于模型使用的是对数线性模型设定,式(15)可以给出的是对数条件方差的预测值E[ln(ht+k)],简单取指数之后并不等于条件方差的期望E[ht+k].因此在进行多步测时,不能借助式(15)直接求取期望,而是需要前计算式(15)指数值再计算结果的期望值,而这需要用到zt和ut的分布信息.考虑到直接根据(zt,ut)的分布来推导ht的计算复杂性较高.

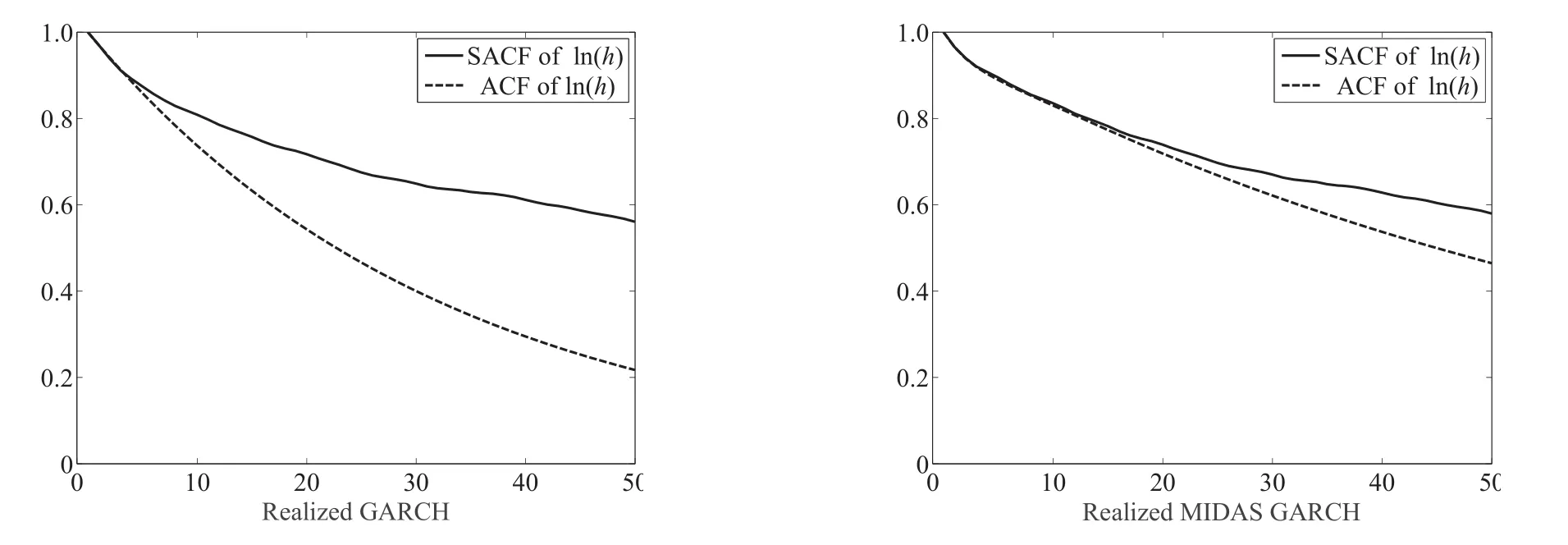
图2 已实现混频数据抽样GARCH和已实现GARCH对于SPY日波动率的ACF拟合Fig.2 The fitted ACF of SPY’s daily volatility for realized MIDAS GARCH and realized GARCH

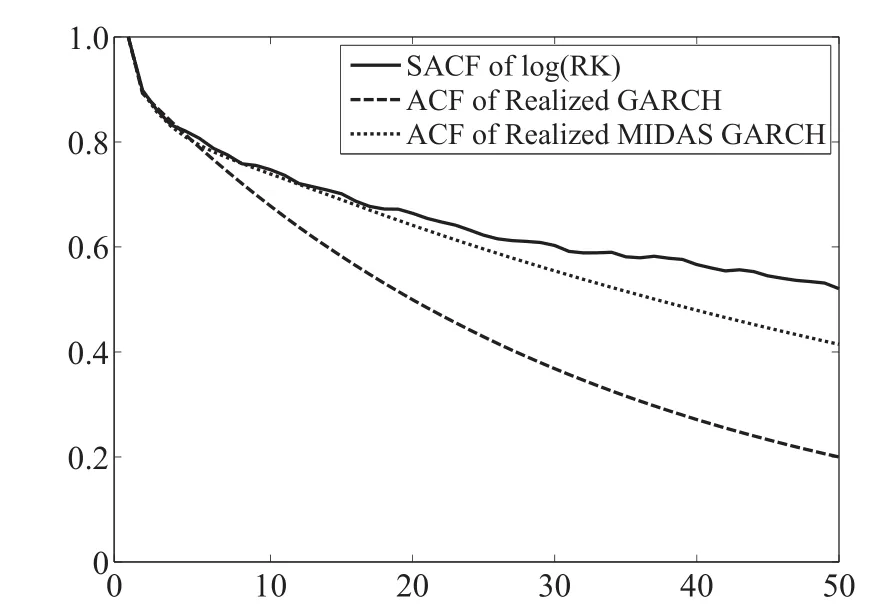
图3 已实现混频数据抽样GARCH和已实现GARCH对于SPY已实现测度的ACF拟合Fig.3 The fitted ACF of SPY’s realized volatility for realized MIDAS GARCH and realized GARCH

本文采用更加简便的蒙特卡洛模拟方法来获得预测值.关于随机数的生成方式,本文沿袭Lunde等[9],采取bootstrap的方法从样本内估计出残差中抽样,进而模拟出ht+k的分布.这样的做法较直接从正态分布里面抽样更贴近实际数据.

样本外预测采用滚动窗口方式进行,以最后的500个交易日为样本外数据,最大样本外预测步长为20步,考虑到数据集的总长度,估计窗口设定为2 400个交易日.对于每个交易日而言,本文模拟M=5 000条未来20日的收益率/已实现测度序列,使用的Ct+j+1(记为t+j+1)从估计窗口中的2 400组残差中有放回抽样计算得到.对于给定的时刻t的k步样本外预测,直接使用平均值来模拟期望值,即

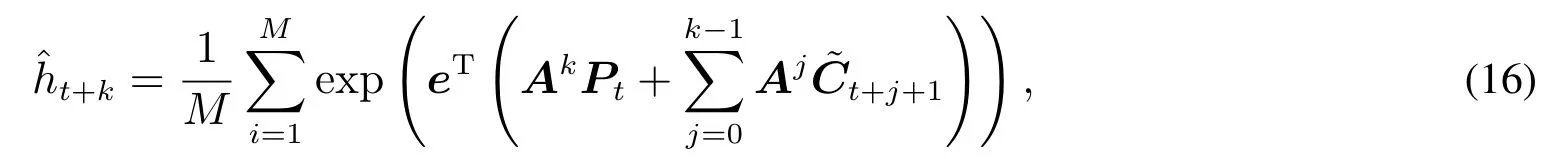
其中22维向量eT=(1,0,...,0).

需要指出的是,这里的多步预测是指未来“第k天”的波动率水平,而不是未来“k天累计”的波动率水平8“k天累计”存在高估低估相互抵消的状况,并不如直接考察“第k天”更准确..

关于波动率代理变量的选择,传统文献中通常选用的是收益率平方.但这种代理变量本身噪音很大,Andersen等[27]建议使用已实现测度作为真实波动率的代理变量9由于比较的两个模型都使用了该已实现测度,因此这样的选择并不偏向于某一个模型.使用5 min RV并不改变结果..本文为简便起见,选择已实现核估计作为代理变量.由于本文使用的收益率数据为基于“收盘价-收盘价”收益率,而已实现核估计覆盖的是“开盘价—收盘价”收益率,故需要对其进行比例变换,将其均值调节到和“收盘价-收盘价”收益率的方差一致10关于类似调节的更多信息,可以参见文献[28]..

遵循Patton[29]的建议,使用稳健损失函数(robust loss function)的进行评价,这种损失函数结合已实现测度,可以给出预测能力的一致排序.在稳健损失函数族中,选取均方根误差11文献[29]指出的是稳健损失函数是MSE,由于RMSE更常用且是MSE的保序变换,本文汇报结果时使用的RMSE,计算统计显著性时基于MSE.常见的平均绝对误差(MAE)指标并不是稳健损失函数.因篇幅所限,本文仅选取了代表性的对称和非对称损失函数作为标准.(RMSE)和准似然函数(QLIKE)两个损失函数作为评价指标.其中RMSE是对称损失函数,QLIKE是非对称损失函数,前者对波动率高估和低估惩罚力度相同,后者对波动率低估有着更大的惩罚力度.本文使用Diebold-Mariano(DM)统计量来刻画不同模型损失函数差别的显著性.

表4和表5分别给出了模型在以RMSE和QLIKE为评价指标下的多步预测的结果.其中包括波动率多步预测的损失函数值,差距值以及DM统计量数值和显著性.

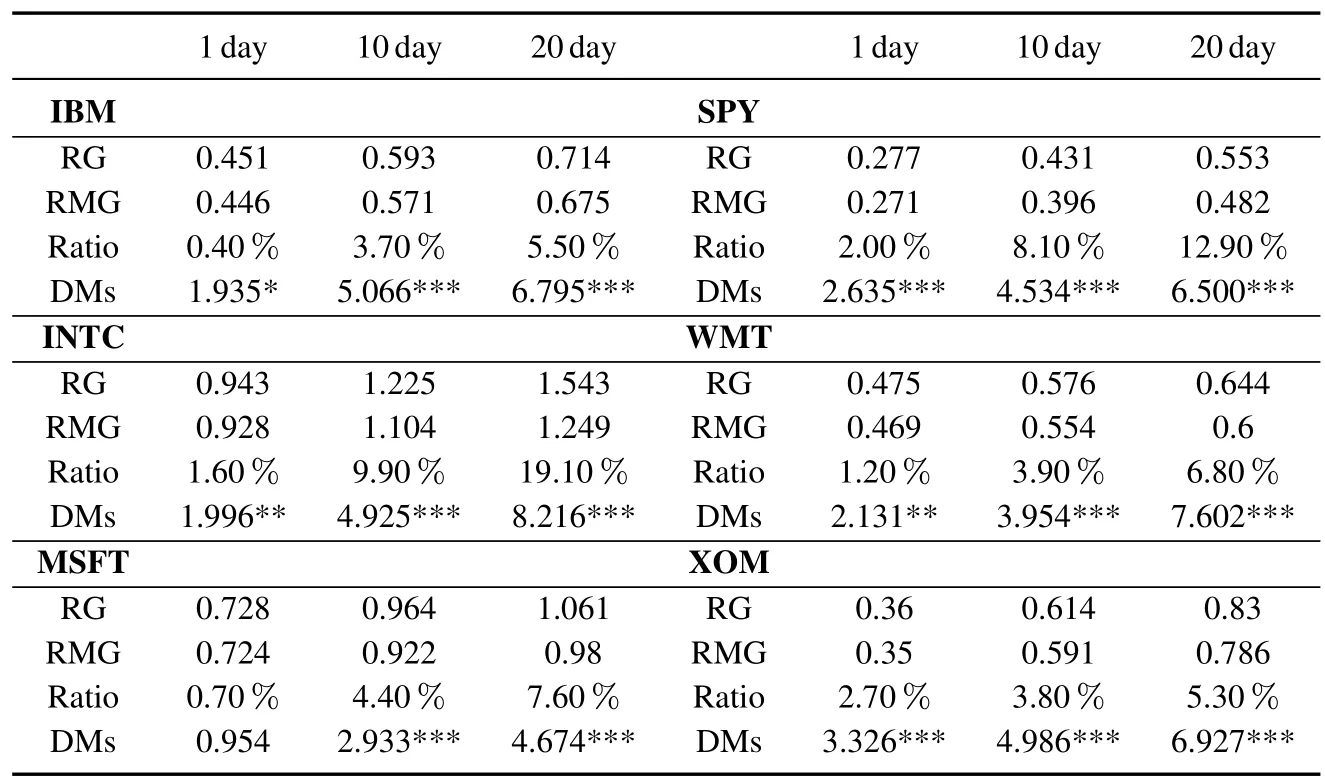
表4 以RMSE为损失函数的多步预测结果Table 4 Loss of multi-steps forecasts based on RMSE

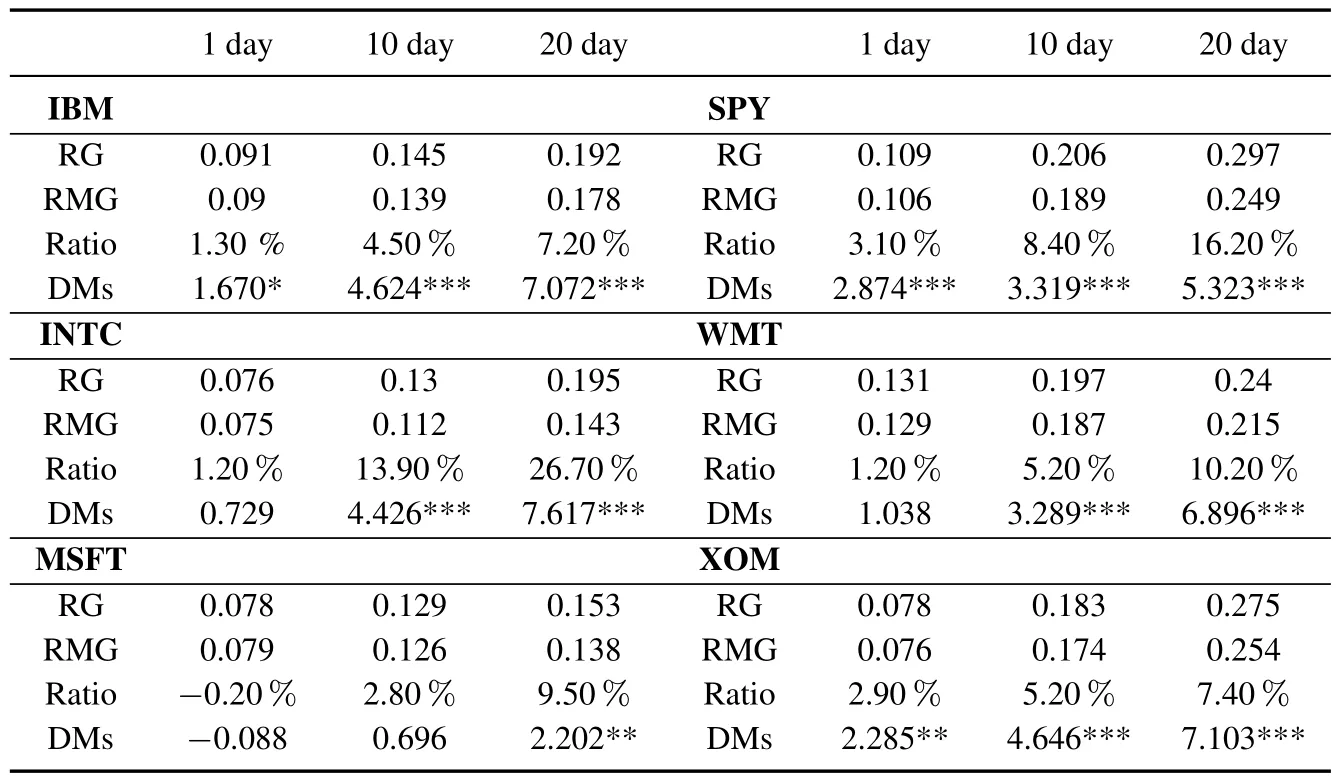
表5 以QLIKE为损失函数的多步预测结果Table 5 Loss of multi-steps forecasts based on QLIKE

为了直观的定义RG模型以及RMG模型在波动率预测上的差距,给定损失函数的值,定义差距为

可以看出,RMG模型除了对MSFT在QLIKE指标下一步预测损失函数较RG高0.2%以外(该差距对应的DM统计量仅为0.088,并不显著),对于其余所有预测期,所有序列的两种损失函数下,RG的损失函数都比RMG大.并且这种差距随着预测期的拉长而进一步加大.DM检验的结果显示,在绝大多数情况下,两个模型波动率预测能力的差距至少在5%水平上是显著的.

多步预测的差异的一个重要原因是RMG模型的长期波动信息加权的系数经过历史数据的训练,能够更好的捕捉波动率序列的相关性.加入长期波动信息还有另外的一个好处:由于本质上是已实现测度的加权平均,其变动较原始波动率更为平缓,在波动率剧烈变化的时候可以提供更稳定的信息,防止条件方差的预测对短期异常波动反应过度.

4 结束语

本文在Hansen等[6]提出的已实现GARCH模型的基础上,提出了在波动率长记忆性建模和多步预测上更具有优势的已实现混频数据抽样GARCH模型,模型在仅增加两个系数的情况下可以容纳更丰富的自相关结构.基于指数和个股的实证结果表明,相比于已实现GARCH模型,已实现混频数据抽样GARCH模型对数据的拟合能力更强,模型的内部一致性更好,能够更好的描述实际数据中波动率相关性缓慢下降的现象.在常用的稳健损失函数下,已实现混频数据抽样GARCH模型的样本外多步预测能力优于已实现GARCH模型,并且这种优势在统计上显著,改进幅度随着预测天数的增加而增大.