不完全无误判金标准下二重抽样设计中样本量的确定
2018-03-01邱世芳曾小松
邱世芳,曾小松
(重庆理工大学 理学院, 重庆 400054)
1 背景
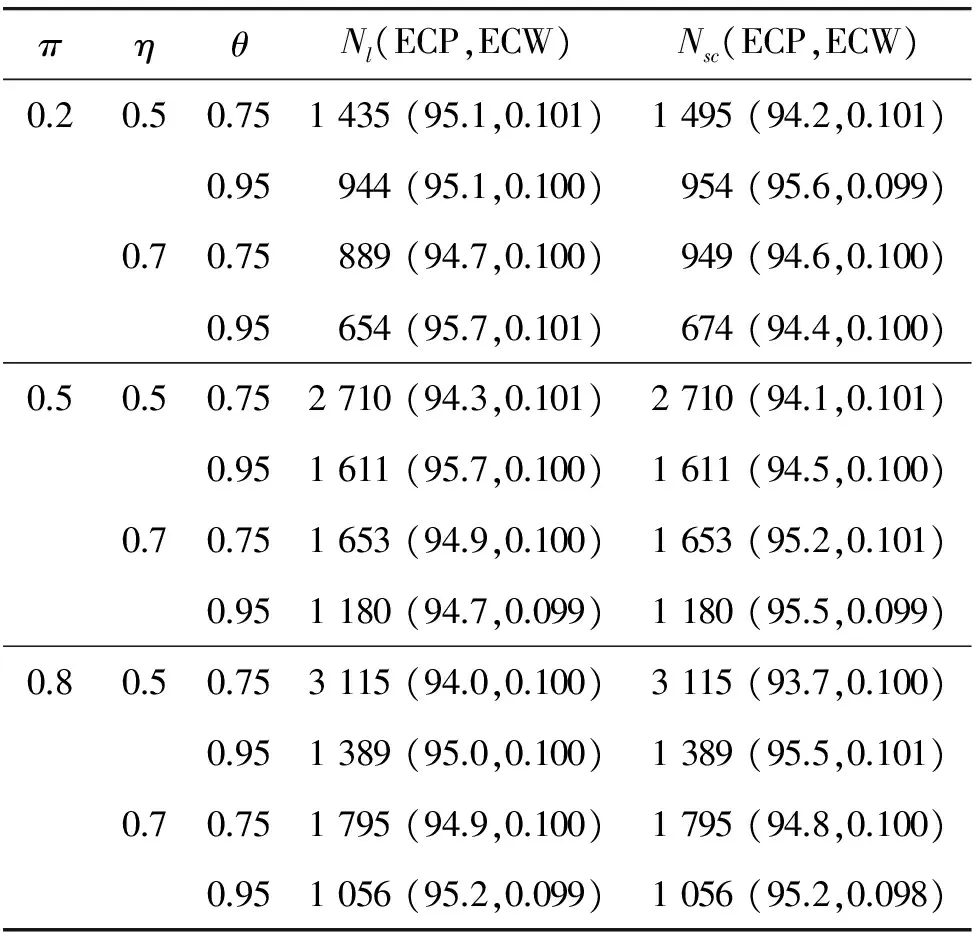
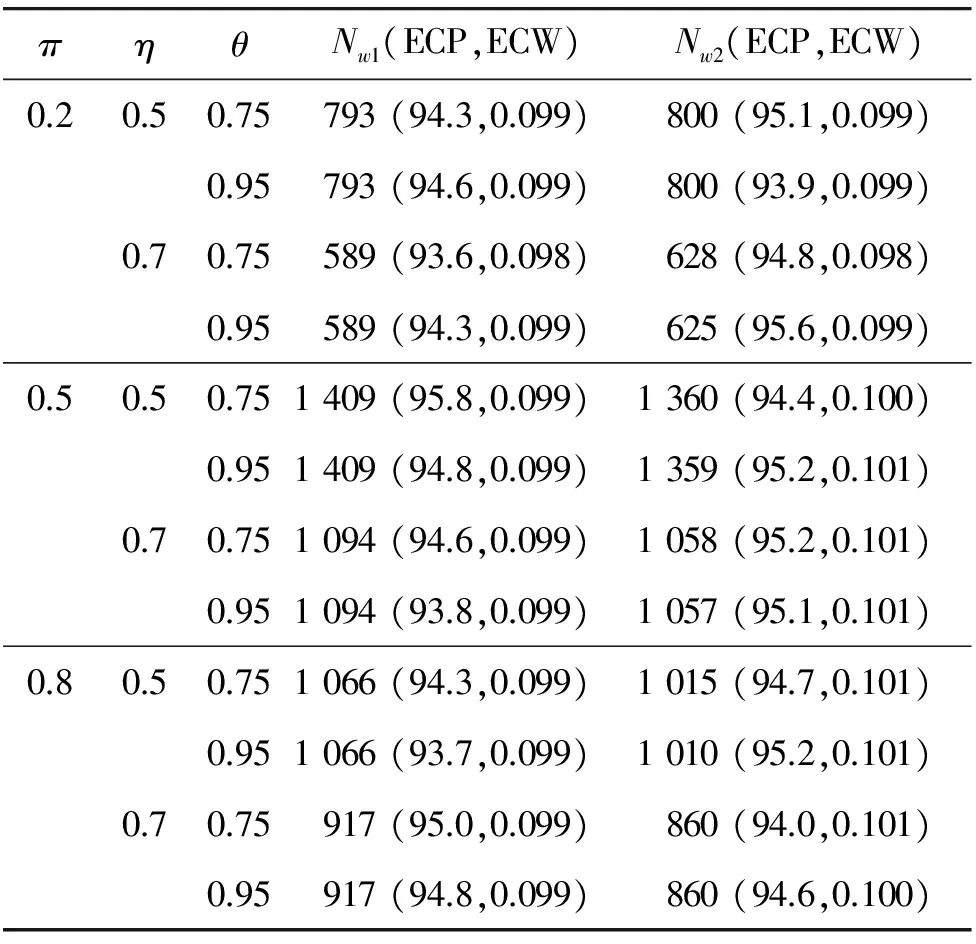
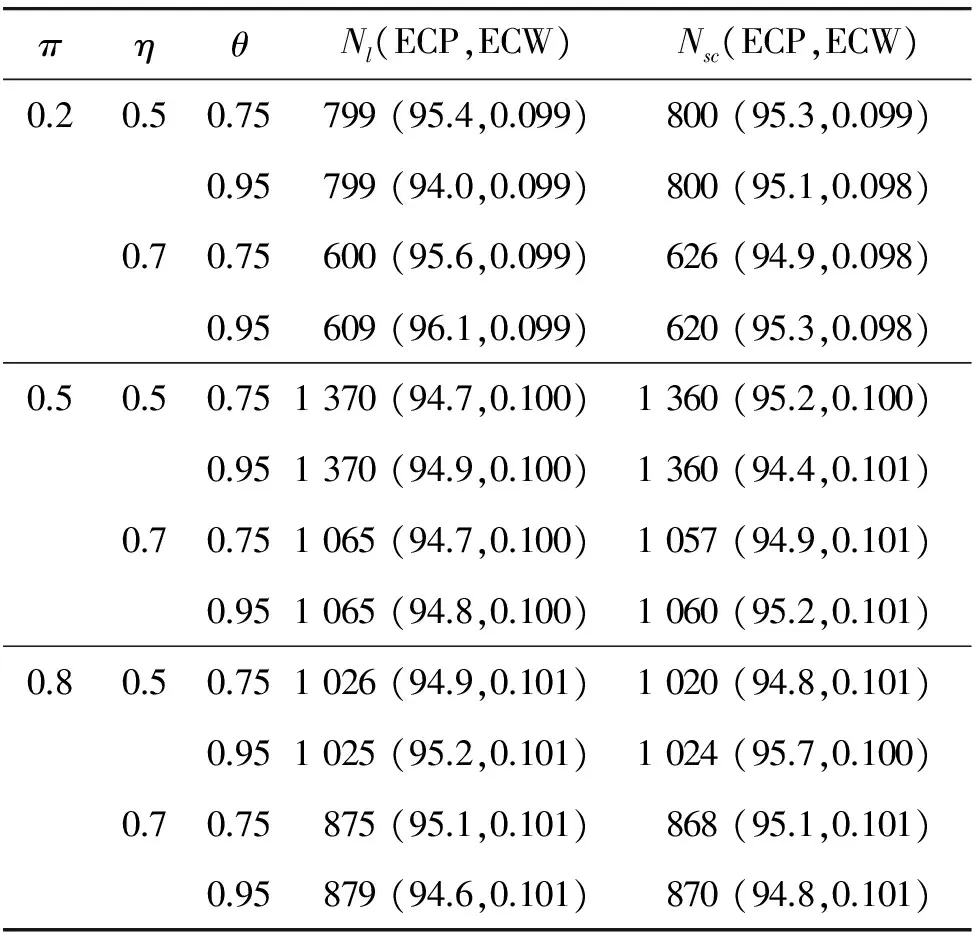
在生物医学和流行病学研究中,为了分析一种疾病的流行率,人们通常使用价格便宜的筛检方法对感兴趣的个体是否感染这种疾病进行第1次临床诊断。但是,这种筛检方法经常导致因不可忽略的诊断误差而出现存在误判的分类数据;另一方面,虽然可以选择一种完全准确的金标准检验,但是这种检验具有价格昂贵、耗时长而且对检验个体有副作用等不足。为了克服这两种方法的不足,常采用二重抽样方法获得部分核实数据,即从感兴趣的总体中随机抽取N个个体,对每个个体都使用筛检方法进行诊断检测,然后再从中随机抽取n(n 在完全无误判的金标准存在时,已有文献对基于部分核实数据的统计推断问题进行研究。例如:Boese[4]对二重抽样设计下有假阳性错误分类时,提出了关于二项分布参数的几种基于似然的近似区间估计;Morvan[5]对筛检过程的准确性以及两阶段调查中疾病流行率的修正估计的准确性提出了两种评价方法;对于单个样本情形,Tang等[3]基于疾病的流行率提出了有实际意义的统计假设,并对此假设考虑了Score检验统计量、似然比检验统计量以及两种Wald型检验统计量,从大样本的角度考虑了渐近的检验过程以及从小样本的角度考虑了近似非条件的检验过程;Tang等[6]基于上述检验统计量提出了关于疾病流行率的12种区间估计方法;Qiu等[7]分别从显著性检验的角度和置信区间的角度研究了疾病流行率显著性检验的样本量的计算公式。对于两组独立样本情形,Tang等[8]基于疾病流行率之差考虑了两组独立样本下疾病流行率的显著性差异的假设检验问题,分析了多种检验统计量(如Score或者Score型检验)的大样本的渐近检验过程和小样本的近似非条件的检验过程,并从检验功效的角度研究了样本量的确定问题; Qiu等[9]基于比例差对不同组的流行病治愈率的等价性评价进行了研究,从置信区间的角度提出了等价性检验中基于比例差的置信区间的估计方法。 以上内容都是基于有完全无误判金标准存在时部分核实数据的研究。事实上,完全无误判的金标准通常是不存在的,接受核实验证的个体通常接受的是不完全无误判金标准检验。当这种不完全金标准检验比筛检有更高的敏感度和特异度时,这样的二重抽样设计仍然可以降低统计推断的偏差,因而基于不完全无误判金标准下的核实数据的统计推断更具有现实意义和实际研究价值。一个典型的例子是Nedelman[10]利用二重抽样方法对疟疾病的流行率进行了研究,根据年龄的不同将总体分为了7个年龄组。首先初级的显微镜医生对每一个年龄组的个体进行检验,然后从中随机抽取一部分个体再接受高级显微镜医生的检验,从而得到部分核实数据。在此研究中,高级显微镜医生虽然比初级医生有更高的敏感度,但是他们的检验仍然有误判可能性。基于这样的部分核实数据,Qiu[11]在没有假阳性假定下对疾病流行率的区间估计进行了研究,考虑了两种模型下的多种有效的区间估计方法。但是,实验样本量的确定问题是实际医务工作者最为关心的问题之一,而从区间估计的角度对该问题的研究还没有文献涉及,因此本文对不完全无误判金标准下的二重抽样设计中所需要的样本量进行研究。 假设从感兴趣的总体中随机抽取N个个体并用筛检方法进行检验,检验结果用变量J表示,J=1表示阳性,J=0表示阴性。然后从抽取的N个个体中再随机抽取n个个体接受不完全无误判金标准检验,检验结果用变量S表示,S=1表示阳性,反之则表示阴性。二重抽样的数据结构如表1所示。 表1 二重抽样的数据结构 假设D表示个体患病状态变量,D=1表示患有疾病,反之表示正常。令π=Pr(D=1),η=Pr(J=1|D=1)和θ=Pr(S=1|D=1),即η和θ分别表示筛检和不完全金标准检验的敏感度。本文考虑不存在假阳性误判的情形,因而它们的特异度皆为1。 假定两种检验方法满足条件独立性,即Pr(J,S|D)=Pr(J|D)Pr(S|D)时,Nedelman[10]提出了一种模型(记为模型1),其概率结构如表2所示。 表2 模型1的概率结构 令m=(n11,n10,n01,n00,x,y),则在此概率模型下m=(n11,n10,n01,n00,x,y)的似然函数为: L1(m;π,η,θ)=A1(πηθ)n11(π(1-η)θ)n10(πη(1-θ))n01(1-π(η+θ-ηθ))n00(πη)x(1-πη)y= A1πn-n00+xηn+1+x(1-η)n10θn1+(1-θ)n01(1-π(η+θ-ηθ))n00(1-πη)y 其中A1是与参数无关的常数,其对数似然函数为 l1(m;π,η,θ)=C1+(n-n00+x)logπ+(n+1+x)logη+n10log(1-η)+n1+logθ+ n01log(1-θ)+n00log(1-π(η+θ-ηθ))+ylog(1-πη) (1) 其中C1=logA1为常数。 令λ1=Pr(S=1|J=1),λ2=Pr(S=1|J=0)和p=Pr(J=1),则λ1=θ,λ2=π(1-η)θ/(1-πη),p=πη,因此对数似然函数(1)变为: l1(m;λ1,λ2,p)=C1+n11logλ1+n01log(1-λ1)+ n10logλ2+n00log(1-λ2)+(n+1+x)logp+(n+0+y)log(1-p) 则λ1、λ2和p的极大似然估计为: 由此易得到,当n11n00≥n10n01时,π、η和θ的极大似然估计分别为: (2) (3) 假定两种分类器不具有条件独立性时, Lie等[12]提出了一种模型(记为模型2),其概率模型结构如表3所示。 表3 模型2的概率结构 在此概率模型下m=(n11,n10,n01,n00,x,y)的似然函数为 L2(m;π,η,θ)=A2(π(η-1+θ))n11(π-πη)n10(π-πθ)n01(1-π)n00(πη)x(1-πη)y= A2πn-n00+x(1-π)n00ηx(1-η)n10(1-θ)n01(η+θ-1)n11(1-πη)y 其对数似然函数为: l2(m;π,η,θ)=C2+(n-n00+x)logπ+n00log(1-π)+xlogη+n10log(1-η)+ n01log(1-θ)+n11log(η+θ-1)+ylog(1-πη) (4) 其中A2和C2为与参数无关的常数。 在此模型下,由λ1、λ2和p的定义可得λ1=(η+θ-1)/η,λ2=π(1-η)/(1-πη)和p=πη。采用和模型1类似的方法可得π、η和θ的极大似然估计分别为: (5) (6) 本文假设核实验证比例为κ,即在κ=n/N情况下考虑实验样本量的确定问题。 其中zα/2为标准正态分布的上α/2分位数。为了将置信区间宽度控制在2ω以内,当ω≤π时设zα/2σ=ω,否则π+zα/2σ=2ω。由此得到基于Wald检验的100(1-α)%置信区间宽度控制在指定宽度2ω所需的样本量(即N),其计算公式为: (7) 其中:对于模型1有 对于模型2有 由此容易发现:在模型2下的样本量与不完全无误判金标准的敏感度无关。 3.2.1 基于限制性极大似然估计下方差的Wald置信区间 (8) 此方程组没有显示解,因此可通过一种迭代方法(如牛顿迭代法)获得。 其中:a=π0(N-n00);b=N-y-n00+π0(N-n+0);c=b2-4a(x+n+1)。 在模型2下,有 3.2.2 基于似然比检验的置信区间 两种模型下的似然比检验统计量为 3.2.3 基于Score检验的置信区间 对于模型1,Score函数为: 对于模型2, Score函数为: 则对于假设检验H0:π=π0的Score检验统计量为 或 其中I11的表达式见附录。在原假设下Tsc渐近服从标准正态分布,因而基于Score统计量的(1-α)100%的置信区间[πl,πu]的上下限可利用迭代方法通过以下方程得到: Tsc=±z1-α/2 其中πl,πu分别对应方程中取“+”和“-”得到。 3.2.4 样本量的求解算法 由于基于以上检验统计量Tw2、Tl和Tsc的置信区间都没有显表达式,因此考虑以下搜索算法获得近似样本量的估计: 步骤1 给定π,η,θ,N和κ的值,产生K组随机样本m=(n11,n10,n01,n00,x,y),其中:在模型1中,(n11,n10,n01,n00)~M(Nκ;πηθ,π(1-η)θ,πη(1-θ),π(1-η)(1-θ)+1-π);在模型2中,(n11,n10,n01,n00)~M(Nκ;π(η+θ-1),π(1-η),π(1-θ),1-π)。在两种模型下(x,y)都服从二项分布B(N(1-κ),πη),其中M(·)表示多项分布。 步骤2 基于步骤1产生的每一个样本,计算π的(1-α)100%置信区间,并通过K个置信区间宽度的平均值计算近似的区间宽度,记为2ω*(N)。 步骤3 若2ω*(N)小于(大于)2ω,那么减少(增加)N的值,重复步骤1和步骤2。 步骤4 重复步骤3直到近似的半区间宽度ω*(N)非常接近于给定的区间宽度ω,则N=minN:|ω*(N)-ω|≤0.001},即为满足条件的近似样本量。 通过以上搜索方法获得的基于Tw2、Tl和Tsc的置信区间的样本量公式分别记为Nw2、Nl和Nsc。 为了评价本文所提出方法的效果,考虑将置信水平1-α=0.95下的置信区间宽度的一半控制在ω=0.05下的样本量的确定,并在估计的样本量(即Nw1,Nw2,Nl和Nsc)下,通过模拟分别研究各置信区间的经验覆盖概率和经验覆盖宽度。假设核实比例即接受不完全金标准检验的个体比例κ=0.2,参数设置为π=0.2、0.5和0.8,由于不完全无误判金标准检验不劣于筛检方法,因而对于敏感度设置为η=0.5和0.7,θ=0.75和0.95,总共3(π的取值)×2(η的取值)×2(θ的取值)=12种参数组合进行蒙特卡洛模拟。 在给定参数组合下,估计出样本量Nw1、Nw2、Nl和Nsc,在估计的样本量下,产生2 000个随机样本m=(n11,n10,n01,n00,x,y),基于每个统计量计算相应的置信区间,从而得到置信区间的经验覆盖概率(ECP)和经验覆盖宽度(ECW)。模型1的模拟结果见表4,模型2的模拟结果见表5。 πηθNl(ECP,ECW)Nsc(ECP,ECW)0.20.50.751435(95.1,0.101)1495(94.2,0.101)0.95944(95.1,0.100)954(95.6,0.099)0.70.75889(94.7,0.100)949(94.6,0.100)0.95654(95.7,0.101)674(94.4,0.100)0.50.50.752710(94.3,0.101)2710(94.1,0.101)0.951611(95.7,0.100)1611(94.5,0.100)0.70.751653(94.9,0.100)1653(95.2,0.101)0.951180(94.7,0.099)1180(95.5,0.099)0.80.50.753115(94.0,0.100)3115(93.7,0.100)0.951389(95.0,0.100)1389(95.5,0.101)0.70.751795(94.9,0.100)1795(94.8,0.100)0.951056(95.2,0.099)1056(95.2,0.098) 表5 基于模型2的95%置信区间宽度控制在2ω=0.1下的近似样本量、经验覆盖概率(%)和经验区间宽度 πηθNl(ECP,ECW)Nsc(ECP,ECW)0.20.50.75799(95.4,0.099)800(95.3,0.099)0.95799(94.0,0.099)800(95.1,0.098)0.70.75600(95.6,0.099)626(94.9,0.098)0.95609(96.1,0.099)620(95.3,0.098)0.50.50.751370(94.7,0.100)1360(95.2,0.100)0.951370(94.9,0.100)1360(94.4,0.101)0.70.751065(94.7,0.100)1057(94.9,0.101)0.951065(94.8,0.100)1060(95.2,0.101)0.80.50.751026(94.9,0.101)1020(94.8,0.101)0.951025(95.2,0.101)1024(95.7,0.100)0.70.75875(95.1,0.101)868(95.1,0.101)0.95879(94.6,0.101)870(94.8,0.101) 模拟研究表明:在基于限制性极大似然估计下方差的Wald置信区间、似然比置信区间和Score置信区间确定的样本量下,它们的经验覆盖概率接近事先给定的置信水平,且半区间宽度很好地控制在ω以内,因而基于这3种方法确定的样本量准确有效。但是,在基于非限制性极大似然估计下方差的Wald置信区间确定的样本量下,其经验覆盖概率不能保证其接近给定的覆盖概率。其次,随着患病概率的增大,要使95%的置信区间宽度控制在2ω以内,所需要的样本量就越大,随着两种检验的敏感度的增大,所需的样本量相应减少。通过对比4种方法可以看到:模型1基于非限制性极大似然估计下方差的Wald置信区间、似然比置信区间和Score置信区间确定的样本量很接近,没有显著差别,只有当π比较小的时候相差较大,限制性极大似然估计下方差的Wald置信区间与其他3种方法相差较大;而模型2基于限制性极大似然估计下方差的Wald置信区间、似然比置信区间和Score置信区间确定的样本量相差不大,没有显著差异,基于非限制性极大似然估计下方差的Wald置信区间与这3种方法所计算的样本量大概相差40。最后,在相同的参数设置下,基于模型2所需要的样本量通常比模型1要小。因此,当两种检验不满足条件独立性时,应考虑模型2的统计分析。 首先,对于引言中的疟疾数据,采用本文提出的方法进行研究。由于篇幅的限制,仅列出小于1岁的年龄组的分析结果,其他年龄组的结果不再一一列出。此年龄组的观测数据为n11=165、n10=8、n01=7、n00=80、x=1736、y=799,即n=260、N=2795。通过数据易知:核实数据的比例约等于0.09,在模型1中参数π、η和θ的极大似然估计分别为0.712 7、0.957 8和0.959 3,在模型2中参数的极大似然估计分别为0.711 5、0.959 5和0.961 0。因此,在样本量的估计中,令κ=0.1,π=0.70,η=0.95,θ=0.95,置信水平为95%,半区间宽度ω=0.05,利用本文提出的样本量估计方法,分别得到两种模型下的样本量的估计值,并计算在估计的样本量下95%置信区间的经验覆盖概率和经验覆盖宽度。在模型1下,Nw1=786,Nw2=846,Nl=816,Nsc=856,其经验覆盖概率(覆盖宽度)分别为92.3%(0.097 7),96.1%(0.100 4),95.6%(0.100 3)和95.1%(0.100 7);在模型2下,Nw1=757,Nw2=800,Nl=799,Nsc=813,其经验覆盖概率(覆盖宽度)分别为93.5%(0.097 6),95.1%(0.099 8),95.4%(0.098 7)和95.3%(0.101 4)。由此可见,要使95%的置信区间宽度控制在0.10内,现有的样本量是满足的。 其次,对Qiu等[7]使用的移植时年龄小于20岁的再生障碍性贫血患者数据进行分析,原始数据为:n11=6、n10=4、n01=3、n00=18、x=12、y=49,即n=31、N=92。在k=0.3,π=0.4,η=0.55,θ=0.75且置信水平为95%、半区间宽度ω=0.05下,基于4种方法在模型1下的样本量分别为Nw1=1 424,Nw2=1 534,Nl=1 424,Nsc=1 454,模型2下样本量分别为Nw1=866,Nw2=837,Nl=841和Nsc=840。 在有金标准的情况下(Qiu等[7])结果为:Nw1=650,Nw2=656,Nl=657和Nsc=665。通过比较可以看到:有金标准所需的样本量比没有金标准所需样本量小,并且无论在哪种情况下现有的样本量都不能使95%的置信区间宽度控制在0.10内。 本文在不完全无误判金标准下,基于部分核实数据从置信区间的角度研究检验所需的样本量,分别考虑了两种Wald检验、似然比检验和Score检验4种方法在两种模型下样本量的确定情况,然后对这些方法进行模拟研究,通过经验覆盖率和区间宽度评价本文所提出方法的准确性。通过模拟结果发现:在相同的参数设置下,基于模型2所需样本量比模型1小,且样本量的大小与不完全无误判金标准检验的敏感度θ无关。基于限制性极大似然估计方差的Wald检验、似然比检验和Score检验的样本量公式具有良好的统计性质,在估计的样本量下的置信区间的经验覆盖概率和经验覆盖宽度都很接近给定的置信水平和区间宽度,因而可推荐用于实际应用中。 模型1假设两种检验满足条件独立性,这个条件在实际中不一定满足,所以在实际应用时要先判断用于诊断的检验方法是否满足条件独立性。模型2的假设在实际中同样可能不成立,所以应根据具体实际情况来选择相应的模型。通过对实际数据的分析可以看到:本文研究成果具有实际应用价值,可为医务工作者提供指导。本文从经典的频率统计方面对样本量的问题进行研究,在未来的研究中还可考虑采用贝叶斯等方法。 [1] TENENBEIN A A.A double sampling scheme for estimating from binomial data with misclassifications[J].Journal of the American Statistical Association,1970,65:1350-1361. [2] YIU C F,POON W Y.Estimating the polychoric correlation from misclassified data[J].British Journal of Mathematical and Statistical Psychology,2008,61:133-161. [3] TANG M L,QIU S F,POON W Y,et al.Test procedures for disease prevalence with partially validated data[J].Journal of Biopharmaceutical Statistics,2012,22:368-386. [4] BOESE D H,YOUNG D M,STAMEY J D.Confidence intervals for a binomial parameter based on binary data subject to false-positive misclassification[J].Computational Statatistics and Data Analysis,2006,50:3369-3385. [5] MORVAN J,COSTE J,ROUX C H,et al.Guillemin F.Prevalence in two-phase surveys:accuracy of screening procedure and corrected estimates[J].Annuals of Epidemiology,2008,18:261-269. [6] TANG M L,QIU S F,POON W Y.Confidence interval construction for disease prevalence based on partial validation series[J].Computational Statistics and Data Analysis,2012,56:1200-1220. [7] QIU S F,POON W Y,TANG M L.Sample size determination for disease prevalence studies with partially validated data[J].Statistical Methods in Medical Research,2016,25(1):37-63. [8] TANG M L,QIU S F,POON W Y.Comparison of disease prevalence in two populations in presence of misclassification[J].Biometrical Journal,2012,54(6):786-807. [9] QIU S F,POON W Y,TANG M L.Confidence intervals for proportion difference from two independent partially validated series[J].Statistical Methods in Medical Research,2016,25(5):2250-2273. [10] NEDELMAN J.The prevalence of malaria in Garki,Nideria:double sampling with a fallible expert[J].Biometrics,1988,44(3):635-655. [11] QIU S F,LIAN H,ZOU G Y,et al.Interval estimation for a proportion using a double sampling scheme with two fallible classifiers[J].Statistical Methods in Medical Research,2016.DOI:10.1177/0962280216681599. [12] LIU R T,HEUCH I,IRGENS L M.Maximum likelihood estimation of the proportion of congenital malformation using double registration systems[J].Biometrics,1994,50:433-444. 附录 Score检验统计量的有关推导: 在模型1下, Fisher信息矩阵中各元素分别为: Fisher信息矩阵的逆矩阵中第一个对角元素为: 在模型2下,Fisher信息矩阵中各元素分别为: Fisher信息矩阵的逆矩阵中第1个对角元素为:2 模型与参数估计

2.1 模型1及其参数估计

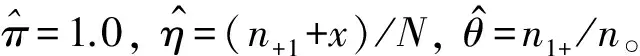
2.2 模型2及其参数估计

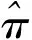
3 样本量的确定
3.1 基于Wald置信区间的样本量
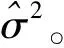
3.2 基于限制性极大似然估计下方差的Wald置信区间、似然比置信区间和Score置信区间的样本量
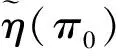
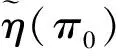
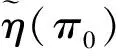
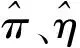
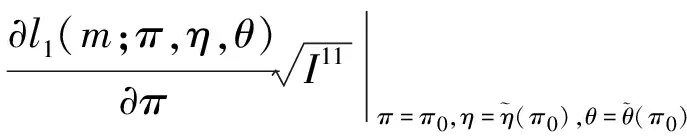
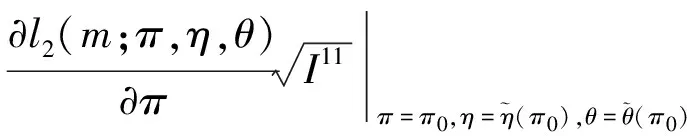
4 模拟研究
5 实例分析
6 讨论
