Hailin Liu

Institute of Logic and Cognition,Sun Yat-sen University

liuhlin3@mail.sysu.edu.cn

Wei Xiong

Institute of Logic and Cognition,Sun Yat-sen University

hssxwei@mail.sysu.edu.cn

1 Introduction

The heated debate on the question of what role subjective probabilities might play in game theory[12,11]seems to suggest something important about the standard account of game theory and its relation to decision theory.At first glance game theory and decision theory are kindred,which one may expect from their similar subject matter,and their related concepts and approaches.Game theory is concerned with rational behavior of decision makers who are conscious that their success in making choices depends on the other agents’decisions.Decision theory investigates the appropriate account of rational choice in single-agent decision problems where an individual selects the optimal option from the set of feasible choices.Game theory can thus be regarded as a generalization of decision theory,which leaves to decision theory the special case of individual decision problems or games against nature.As a matter of fact,this view of game theory was already expressed explicitly by Harsanyi and Myerson in their influential books:

“[...]our theory of rational behavior in game situations will represent a generalization of Bayesian decision theory.”([10],p.47)

“[...]game theory can be viewed as an extension of decision theory(to the case of two or more decision makers),or as its essential logical fulfillment.”([16],p.5)

Based on this view,many game theorists attempt to develop a unifying approach to dealing with both strategic situations and single-agent decision problems.It turns out that it is almost impossible to unify these two frameworks possibly because of their distinct conceptual foundations.

As Kadane and Larkey point out,however,there exists a curious gulf between classical game theory and decision theory,particularly the classicalsubjective expected utilitytheory developed by[23]:

“It is a curiosity of intellectual history that these two lines of inquiry havehadsolittletodowithoneanotherdespitetheircommonheritage.”1These two approaches the authors refer to are expected utility theories developed by von Neumann&Morgenstern[18]and Savage[23]with respect to objective and subjective probability respectively.([12],p.114)

On the one hand,the theory of subjective expected utility deals with individual decision problems by means of quantitative decision models.In such a model,a rational agent is assumed to have preferences obeying Savage’s axioms and to represent her uncertainty about states of the world in terms of asubjectiveorpersonalprobability,which reflects the agent’s degree of belief about the states.Then rational decision is defined as the act that maximizes expected utility with respect to her subjective probability.This approach has been widely perceived as a normative paradigm of rational decision making under uncertainty.It is clear that rational agents’beliefs concerning uncertainty about the nature play a crucial role in the standard account of rational choice.On the other hand,in traditional game-theoretic framework strategic situations are usually analyzed by using standard solution concepts likeminimaxorNash equilibrium.According to these solution concepts,players’expected utilities are evaluated with respect toobjectiveorphysical probability,which is based on known facts about random,observable physical systems such as roulette wheels and rolling dice,thereby implying a “logical”or“necessitarian”interpretation.As Kadane and Larkey point out,players’beliefs about the others’possible actions do not play any essential role in these traditional solution concepts.In view of this,it seems fair to say that the standard accounts of game theory and its fundamental solution concepts appear quite unsatisfactory from the decision-theoretic perspective,not to mention whether or not game theory is a generalization of decision theory.

How may players’subjective expectations of other players’likely behavior enter into any account of rational behavior under strategic circumstances?This is the main issue raised by Kadane and Larkey in their paper.In the ensuing years,a subjective view of probability has been increasingly explored in the context of strategic situations.A great deal of effort have been devoted to developing alternative solution concepts by taking subjective probabilities into account.In particular,the concept ofrationalizabilityproposed independently by[4]and[20]identifies explicitly strategic rationality with individual rationality in the sense of maximizing expected utility like Savage’s theory,together with common knowledge of rationality.This kind of line of reasoning about strategic rationality was further explored in[5,2,9,25,17].The essential idea behind these approaches is to derive game-theoretic solution concepts from more primitive assumptions concerning individual rationality as explored in the theory of subjective expected utility[23].More precisely,a rational player in a game should first form a subjective probability over the other players’strategies,and then choose an action to maximize her own expected utility with respect to it.The is exactly in a similar vein of standard decision theory.

The main purpose of this paper is to provide some further insight into the fundamental issue of what role the concept of subjective probabilities may play in the context of strategic interactions.First we would like to point out some problematic issues in the traditional approach to analyzing strategic games,which are closely related to the role of subjective probabilities in the theory of games.We shall show that these troubles associated with the traditional game-theoretic framework can be evaded by strictly sticking to a decision-theoretic account of game theory using subjective probabilities.In particular,we will use the notion of rationalizability as an example to demonstrate this viewpoint.Finally,we conclude the paper with a few remarks concerning the role of subjective probabilities in game theory.

2 Rationality in Games

Considerthefollowinghypotheticalsituationinwhichacoupleisinvolved.Both of them agree to go out together but forget the place they had agreed upon.Each of them has to make a choice between a concert and a sport event.The woman prefers to gotoaconcertwhilethemanwantstogotoasportevent.Iftheygotodifferentplaces,each of them would be equally unhappy enjoying the entertainment.Moreover,there is no way that they can communicate with each other and can figure out which place where the other person is likely to go,i.e.,neither of them has a mobile phone.In this case,what should each of them do when facing this situation?

Situations like this,where the outcome of an agent’s action depends on the actions of all the other agents involved,are calledstrategic.The above question is the main issue that game theory is concerned with.We may model this strategic situation asatwo-playernormalformgame.Thebasicproblemofgametheorythenis,roughly stated,somehowtofigureoutforeachofthemwhichchoicewouldbeanoptimalone.However,this problem is too indeterminate to be resolved without any further specification.First,it is typically assumed that each of them has full knowledge of the game in normal form.More specifically,both of them are aware of the other person’s possible alternatives(strategies)and they both know each other’s preference over the outcomes of all possible strategy combinations,which are in general represented by expected utilities of payoff functions.Moreover,it is often assumed that each of them is rational,in the sense,according to the standard account of rationality in traditional gametheory,thattheyareomniscientanddeductivelyomnipotentmaximizersoftheir own expected utility with respect to the chance moves of the game.These are the two basic assumptions of classical game theory.

In many real-world scenarios the first assumption is quite unrealistic and thereforethepredictionpowerofgametheoryappearsdubious.Forexample,thecomplete knowledge assumption seems to be too demanding even for highly intelligent people engaged in competitive market problems.Although this is a serious idealization of strategic interactions in actual situations,it is necessary to point out that game theory could not provide too many insights without this idealized requirement.Thus we should maintain this basic assumption by following standard game theory.

Nevertheless,the second assumption concerning the rationality of players needs some consideration.First,it is natural to ask the following question:What does“rational”exactly mean as used in the rationality assumption?Its exact meaning is not clear enough according to standard game theory.As Luce and Raiffa point out:

“Though it is not apparent from some writings,the term ’rational’is far from precise,and it certainly means different things in the different theories that have been developed.”([14],p.5)

Recall that according to orthodox decision theory a decision maker is said to berationalif the agent makes decisions consistently in pursuit of her own objectives.Formally,this is generally interpreted as maximization of her own expected utility with respect to herpersonalbeliefs about the likelihood of states of the world.Traditional gametheoryalsoregardstheprincipleofmaximizingexpectedutilityasacanonofrational behavior in strategic interactions,whereas assumes that in games each player’s objective is to maximize the expected value of her own payoff with regard toobjectiveprobability.It is worthwhile noting that this notion of probability generally does not include any information concerning players’beliefs about her opponents’possible moves and thus has a “frequency”or“logical”interpretation,which is different from the idea of rational choice under uncertainty as formalized within the subjective expected utility theory by Savage[23].From a pure decision-theoretic point of view,the basic assumption concerning players’rationality certainly ignores essential information related to players’personal beliefs,which in turn renders the suggested solution concepts difficult to be supplied with a decision-theoretic account.We shall discuss some problems of traditional solution concepts in the subsequent section.

Another problem concerning the rationality assumption is that it seems insufficient to assume that the players involved in the game are rational.At least it seems that we should also assume that each player believes the other players to be rational;otherwise,it is almost impossible to offer a general theory to account for irrational players’strategy choices.As a matter of fact,mutual knowledge of rationality is not sufficient as well in order to deduce some traditional game-theoretic solution concepts,for example,backward induction solution.So game theorists usually assumes that the rationality of the players iscommon knowledgeamong the players.The term “common knowledge”was first introduced by[13]and later formalized by[1].Roughly speaking,a proposition is said to becommon knowledgeamong a group of players if each player knows it to be true,knows that every other players knows it to be true,knows that every other players knows that every other players knows it to be true,and so onad infinitum.

There is an extensive literature devoted to the discussion of the assumption of common knowledge of rationality in games,see for example,[7,6,21,3,24].Here we do not want to delve into the detailed discussions about this assumption and the related solution concepts of game theory.Instead,we employ the centipede game[22]as a setting within which to illustrate the typical problem associated with the common knowledge assumption,and how subjective probabilities might enter into strategic reasoning in games.The game shown in Figure 2 is a typical representation of a 100-round centipede game,in which player 1 moves first and chooses betweendown(D)andacross(A),and then player 2 chooses betweendown(d)andacross(a).

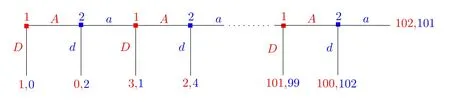
图1:A 100-round Centipede Game

The typical reasoning(commonly known asbackward induction)considered in the literature can be stated as follows:at the last decision node,player 2 gets the turn to move and she prefers to go down than to go across;given this decision,player 1 who moves before player 2 prefers to go down than to go across;working backward leads to a unique solution to the game in which each player’s strategy is to go down whenever it is her turn to choose.The outcome of this recommended solution is that player 1 go down at the first decision node.Of course,this pattern of behavior is intuitively unappealing,especially if the number of the rounds is large.In fact,experimental evidence[15]shows that human decision makers seldom follow the strategy suggested by backward induction reasoning.

At this point,one may reasonably suspect that there is something wrong with either the assumption of common knowledge of rationality or the backward induction reasoning.At first glance,the backward induction reasoning seems quite appealing.Upon close inspection,however,it throws away important information in order to make the whole reasoning process work.Consider a player who has to make a decision at round 66 of the above game.What should she do?Backward induction tells her that she should choose going down.However,if the player is rational,she should be able to infer something from the current situation,since it can only arise when both players choose going across at the first 65 rounds.How could this happen?Either the players are rational,but made a mistake at each preceding nodes,or they are not rational at all.In both cases,it seems very difficult to make sense of both the common knowledge assumption and the backward induction reasoning at the same time.

Ontheotherhand,itisworthyofnotingthattheoptimalityofplayer1’schoosing to go down depends essentially on her believing that if she plays across,then player 2 will go down at the second decision node;moreover,player 2’s decision to go down at the second decision node depends heavily on her believing that if she plays across,then player 1 will go down when she gets the turn to choose;each decision to choose down is based on similar considerations.How reasonable is this kind of considerations?Why is it justified for both players to hold this sort of beliefs?This kind of questions seems to suggest that players’subjective beliefs or probabilities might play a certain role in understanding strategic reasoning in games.For instance,what if that both players strongly believe that the other players is going to choose across for at least a number of rounds but without knowing the exact number?It seems quite reasonable to recommend that each player should choose across for a certain number of rounds rather than going down at the first round.For it is rational for player 1 to choose across provided that she believes that if she plays across,then player 2 will go across at the second decision node;similarly,it is rational for player 2 to choose across given this kind of belief.Based on this idea,we might be able to account for some more reasonable solutions to the centipede game.Of course,it is far from clear howthisinformalideacanbepreciselyformulatedwithintheframeworkoftraditional game theory,which thus needs further investigation.

3 Problems with Standard Solution Concepts

Game theory has often been understood as a part of a general theory of rational behavior.Under a standard interpretation,the main goal of game theory is to model and understand rational agents’behavior in strategic interactions in which the outcome of their actions depends not only on what they do,but also on other agents’decisions.Game theorists try to understand strategic interactions by means of constructing various solution concepts,which essentially are rules for predicting how the games will be played.This standard account of game theory is commonly accepted by many traditional game theorists,for example:

“The normative solution concepts of game theory try to provide a clear mathematical characterization of what it means to act rationally in a game where all players expect to act rationally.”([11],p.120)

“Game theory is a bag of analytical tools designed to help us understand the phenomena that we observe when decision-makers interact.”([19],p.1)

In other words,solution concepts of game theory aim at recommending what agents should do in various interactive situations.Thus we should evaluate the solution conceptsthatitproposesinordertofullyunderstandthestandardaccountofgametheory.

The most commonly used solution concept in game theory isNash equilibrium.Informally speaking,a strategy profile(a collection of strategies,one for each player)is a Nash equilibrium if each player’s strategy is abest response2Informally speaking,the notion of best response can be understood as maximizing expected utility with respect to the list of other players’strategies.against the other players’strategies.TheintuitionbehindNashequilibriumisthatitrepresentsasteady statesuchthatnoplayercandobetter byunilaterallydeviating.Althoughtheconcept of Nash equilibrium looks quite appealing and possesses many attractive properties,it is well known that it suffers from numerous problems.Here we shall only briefly review some of them that are related to the issue of subjective probabilities in games.

First,it has been argued that Nash equilibrium cannot be an appropriate criterion for assessing players’rational strategy choices in a game,for it rules out behavior that in fact does not contradict the common knowledge assumption of players’rationality.To illustrate this point,we should make explicit the assumptions that underlie the concept of Nash equilibrium.It is generally understood in the traditional game theory that Nash equilibrium embodies the idea of rational behavior in strategic games based ontheassumptionsofcommonknowledgeofthegamestructureandoftherationality of the players.However,it turns out that the sufficient epistemic conditions for Nash equilibriumaremuchstrongerthanthosetwobasicassumptionsofgametheory(fora detailed discussion see[8]).Common knowledge of the game structure and common knowledge of players’rationality are neither necessary nor sufficient for the concept Nash equilibrium.Instead,it is required that all the playersknowwhat the others will choose in order to arrive at a Nash equilibrium(in pure strategy).More precisely,the concept of Nash equilibrium demands not only that the players should choose according to the principle of maximizing expected utility and expect each other to make decision in the same way,but also that their expectations of how the others will chooseshouldbecorrect.Nomatterwhetherthefirsttworequirementsarereasonable or not,the later one looks extremely stringent and unrealistic.

There is no doubt that once the players have arrived at a Nash equilibrium,neither has any good reason for deviating from her strategy choice unilaterally.But why should the players expect that they will arrive at a particular Nash equilibrium(even in cases where there is one unique equilibrium as outcome)?It is usually assumed that all players have no clue to figure out which strategy the other player is likely to adopt.If this is true,why should each player choose a best response to the strategy chosen by the other players given that she does not know the other players’strategy choices?In view of this,it seems reasonable to claim that the concept of Nash equilibrium assumes too much knowledge about players’behavior,and it imposes too restrictive constraint on the players’beliefs concerning the others’strategic choices.This analysis suggests that these conditions are too strong to derive the Nash equilibrium concept from more primitive decision-theoretic criterion,and thus claiming the notion of Nash equilibrium as a normative solution concept becomes unconvincing.

Now let us put aside the issue of stringent conditions for Nash equilibrium.In Harsanyi’s reply to Kadane and Larkey,Harsanyi writes:

“Kadane and Larkey[...]do not seem to realize that their approach would amount to throwing away essential information,viz.,the assumption[...]thattheplayerswillactrationallyandwillalsoexpecteachother to act rationally.”([11],p.121)

“[..]Kadane and Larkey[...]do not seem to realize how important anormativetheory of rational behavior in game situations is for formulating realistic expectations about the other players’strategies and,eventually,for developing a realistic descriptive-i.e.,explanatory and predictive-psychological theory of game behavior.”([11],p.125)

Here Harsanyi wants to argue that,in contrast with Kadane and Larkey’s proposal,thetraditionalgame-theoreticapproachtostrategicinteractionsattemptstodetermine the outcome of any game by assuming that the players will choose and expect each other to choose in accordance with the suggested solution concepts.This idea certainly makes perfect sense in those case where the structure of the payoffs lead rational players to form similar beliefs about how the others are likely to make decisions.Some games,for example,the strict dominance solvable games,3Here we mean the games whose outcome can be resolved by iterated elimination of strictly dominated actions.do have reasonable solutions.Nevertheless,it is necessary to point out that there are a variety of nontrivial games,with important applications in economics,which generate(sometimes infinitely)many different Nash equilibria.It thus implies that the solution concept of Nash equilibrium is tooweaka criterion for predicting the players’rational behavior in various strategic situations.

In order to illustrate this point,let us reconsider the hypothetical situation described at the beginning of Section 2.This situation can be modeled as the two-player normal form game in Figure 2,in which player 1 chooses a row and player 2 choose a column.The game is often referred to as the “Battle of Sexes”.

It is easy to see that this simple game has two Nash equilibria in pure strategy,namely,(B,B)and(S,S).That is,both outcomes are compatible with the notion of Nash equilibrium.If both players chooseB,then no player has an incentive to deviate;if both players choosesS,then no player has an incentive to deviate;in either case it forms a steady state of play.Regarding the predictive aspect of solution concepts,one may naturally ask which of these equilibria allowed by Nash equilibrium will the players play.Without knowing this,the players may end with playing some strategy combination that in fact is not a Nash equilibrium.This would violate the solution concept that game theorists would like to impose.In view of this,a great deal of effort has been devoted to refining the concept of Nash equilibrium.Yet the searchforauniversalsolutionconceptthatwoulduniquelyanduncontroversiallysingle out a unique outcome did not turn out well.Thus,from a descriptive perspective,the prediction power of game theory becomes extremely questionable as well,especially when there are several equilibria that are consistent with the suggested solution concepts.

Figure 2.A BoS Game

4 Subjective Probabilities and Rationalizability

In the previous sections we have discussed some fundamental problems associated with the standard account of game theory and the standard solution concept.It seems that the traditional approach to strategic interactions does not constitute a decision-theoretic account of game theory,and the standard solution concept of game theory cannot be derived from more primitive decision-theoretic principles.As mentioned before,there is an increasing interest in applying subjective probabilities to strategic situations.Motivated by this idea,many solution concepts have been proposedintheliterature,i.e.,rationalizabilityandcorrelatedequilibrium,whichattempt to reduce theobjectiveknowledge assumed by the standard approach and so move in thedirectionofsubjectiveequilibrium.Inthoseframeworkasubjectiveviewofprobabilities that is used to describe the players’beliefs about the other players’strategy choices is usually adopted.Thus,these approaches to strategic games seem to be more decision-theoretic in spirit.In order to evaluate the success of applying subjective probabilities to games,we shall use the notion of rationalizability as an example to illustrate the basic idea behind a decision-theoretic account of game theory and how it can overcome some limitations of the standard approach.

Theconceptofrationalizabilityproposedindependentlyby[4]and[20]attempts toaddressthequestionofwhatoutcomesareconsistentwiththeplayers’introspective reasoningofeachother’srationalbehavior.IncontrastwiththeconceptofNashequilibrium,rationalizability imposes a rather weak requirement on players’beliefs about her opponents’strategy choices,which turns out to be fully characterized in terms of Bayesian rationality and common beliefs in Bayesian rationality.More precisely,it attempts to characterize rational behavior in strategic situations that is implied merely by common knowledge of the game structure and the rationality of players,without imposing any further constraints on players’beliefs concerning the others’strategy choices.Roughly speaking,a strategy profile isrationalizable(in the sense of BernheimandPearce)ifeveryplayer’sstrategychoicemaximizesherownexpectedutility with respect to some “rational beliefs”,which are compatible with her opponents’rational behavior.In light of this,we can say that this account of rational behavior takes a view of strategic reasoning in games that is deeply rooted in orthodox decision theory,e.g.,Savage’s theory of subjective expected utility([23]).

Unlike Nash equilibrium,the concept of rationalizability is explicitly designed to study rational behavior of players who attempt to deduce their opponents’rational actions from their opponents’preference and from analyses of their opponents’reasoning about their own rational actions.Moreover,as we shall see,the meaning of rationality in the assumption is made quite clear in the framework of rationalizability,which is formally defined as maximizing expected utility with respect tosubjective probabilities.This is essentially the fundamental principle considered in the classical approach to single-agent decision making.To be more specific,rationalizability in normal form games is defined based on the following assumptions:

·A1:Each player employs asubjective probabilityto express her belief about the other players’strategy choice,which cannot conflict with any information available to her.

·A2:Each player attempts to maximize her own expected utility with respect to

hersubjective probabilityregarding her opponents’strategy choices.

·A3:The game structure,including the strategy space and payoff functions,and the fact that each player satisfies A1 and A2 arecommon knowledge.

Under these assumptions,it seems reasonable to expect that a rational player would first form a personal probabilistic belief about her opponents’likely actions,and then opt for a strategy that maximizes her own expected payoff given her subjective belief.In other words,a rational player will use only those strategies that are best responses to some beliefs she might have about her opponents’possible behavior.Note that it is assumed that each player knows the other players are rational in the Bayesian decision-theoretic sense.Thus,her beliefs about her opponents’strategiescannotbe arbitrary,and in fact should be consistent with the expectation that her opponents would adopt only those strategies that are best responses to certain beliefs that they might have.Similarly,her opponents’beliefs should not be arbitrary as well and should be consistent with their expectations.This observation indirectly refutes a criticism raised by Harsanyi:

“If we are not told how he should choose his subjective probabilities,thisstatementamountstonomorethansayingthatheshoulddowhatever he thinks best-without telling him in any way what heshouldthink was best for him to do.”([11],p.122)

It is not the case that the players should take her opponents’being rational into ac-count,andthustheplayers’beliefsconcerningheropponents’strategychoicesshould not contradict with the fact that the others are rational as well.

We can examine a player’s rationality by checking whether the actions chosen by that player are “rational”or not.We say that an action of a player isrationalif it is a best response to somebeliefregarding the other players’behaviors.Recall that the probabilities that lie behind the usual Nash equilibrium concept of game theory must be objective,at least implicitly([12]).We have argued in the previous section that the notion of Nash equilibrium suffers various difficulties as either a normative or a descriptive solution concept.A major reason is that it implicitly admits an objective interpretation of probabilities,which thus excludes the possibility of representing players’subjective beliefs and lacks intuitive appeal in many games.In order to escape from these somewhat implausible constraints on players’expectations,[4]and[20]proposed to use subjective probabilities to model players’beliefs concerning her opponents’strategy choices.

Definition 1In a normal form game,a(correlated)beliefof a player about the other players’strategy choices is assumed to be represented by a personal probability distribution over the set of the other players’strategies.

Definition 2A strategy of a player in a normal form game isrationalif there exists a belief of the player under which the strategy maximizes her own expected utility.

With the aid of these notions,we can now formulate the idea of rationalizability in a more precise way.We say that a strategy of a player isrationalizableif she can justify her strategy choice by explaining that(i)the strategy is rational,(ii)there exists some belief such that that strategy maximizes her own expected utility with respect to her belief,and the probability distribution representing her belief assigns positiveprobabilityonlytorationalactionsofheropponents,and(iii)therearebeliefs of her opponents that make those actions rational and assign positive probability only to her rational actions,and so onad infinitum.This seems that to formally define the concept of rationalizability we have to invoke an infinite process of justification.Thisisageneralconcernwithapplyingthenotionofsubjectiveprobabilitytostrategic situations,which was already explicitly expressed by Kadane and Larkey.

“A possible problem with the theory advocated here is the infinite regress.If he thinks I think he’ll dox,then he’ll doy.If he thinks I think he thinks I think he’ll doy,etc.”([12],p.116)

Nevertheless,there exists an alternative way of defining the concept of rationalizability that circumvents the infinite process.In order to motivate this simpler definition,let us consider a two-player game.Suppose that there are two setsA1andA2of actions of player 1 and 2 respectively.These two sets satisfy the following conditions:the setA1contains an actionof player 1,every action inA1is a best response to a belief of player 1 that assigns positive probability only to actions inA2,and similarly every action inA2is a best response to a belief of player 2 that assigns positive probability only to actions inA1.Given these conditions,it is not difficult to verify that we can construct an infinite sequence of justification as described above.Hence we can conclude that the actionis a rationalizable action for player 1.In light of this,we can thus define rationalizable actions as follows.

Definition 3In a normal form game,an action of a playeriisrationalizableif for each player,there exists a set of actions such that(i)the set of action for playericontains the action of playeri,(ii)for each player,every action in the set of actions specified for her is a best response to some belief of her that assigns positive probability only to lists of actions in the specified sets of actions for the other players.

Notethatthesecondconditionintheabovedefinitionbasicallysaysthateachplayer’s actions can be justifiable by some belief about the other players’strategies,which is basedonthoseactionsofheropponentsthatcanbejustifiableinthesamewayaswell.This is in fact imposed by the assumption of common knowledge of the rationality of the players,which is the the essential idea behind the concept of rationalizability.

Itisnotdifficulttoshowthateachplayerhasatleastonerationalizableactionfor any finite game in the sense that each player has a finite set of actions available.Once we specify the underlying topology for finite games,this existence result turns out to be just an implication of the finite intersection property of compact sets.Another way to see the existence of rationalizable action is to observe that the notion of Nash equilibrium is in fact a special case of rationalizability.To see this,note that in a(mixed strategy)Nash equilibrium,any action of a player used with positive probability is a best response to the list of the other players’strategies.Recall that any finite game has at least one mixed strategy Nash equilibrium.It thus follows that each player’s set of rationalizable actions in finite strategic games is nonempty.

It has been established that the set of rationalizable action coincides with the set of actions that survives iterated elimination of strictly dominated actions.Recall that an action of a player isstrictly dominatedif the player has another strategy that yields her a higher expected payoff than it does,regardless of the other players’strategy choices.Clearly,if a player is rational in the sense of maximizing expected utility,she definitely should not choose those strictly dominated actions.This equivalence result provides another intuitive justification for rationalizability.

Nevertheless,it is worthy of our attention that a player may have more than one rationalizable action in some games.In fact,the concept of rationalizability typically cannot single out a unique strategy profile as the outcome of strategic games.This is simply because that it imposes merely a minimal constraint on how players should form their subjective beliefs about the other players’strategy choice.As Pearce explainsin[20],the insufficient informationavailableto theplayers and therather weak assumptions made about the players’strategy choices together lead to the typical case of indeterminate predictions regarding players’rational behavior.The concept of rationalizabilityoriginallyisnotdesignedtoachievethegoalofuniversallysinglingout a unique strategy as the outcome of any game.Instead,its primary purpose is to address the issue of characterizing rational behaviors in strategic situations constrained merely by assuming that the structure of the game and the rationality of the players are common knowledge,without imposing any further restriction on players’strategy choices.Itseemsthereforethattheconceptofrationalizabilityisjusttheconsequence of common knowledge of the rationality of the players.

Essentially,the concept of rationalizability employs the notion of subjective probabilities to represent players’beliefs about her opponents’strategy choices,and attempts to account for rational behavior based the rather weak assumption of common knowledge of rationality.In view of this,it thus admits a variety of possibilities to refine the concept of rationalizability by imposing stronger requirements on players’beliefs.In fact,as a special case of rationalizability,the concept of Nash equilibrium not only requires each player’s strategy to be rational for some beliefs,but also puts further constraints on the players’beliefs about her opponents’strategy choices.In particular,in each equilibrium it requires that each player’s belief regarding the other players’likely actions should be correct in the sense that players’beliefs coincide with the component in the equilibrium profile.And many other refinements of rationalizabilityhavebeenproposedintheliterature,forexample,cautiousrationalizability[20]and perfect rationalizability[4].The basic idea behind these refinements istorestrictplayers’beliefsabouttheotherplayers’possiblestrategiesbyconsidering some further requirements.

5 Concluding Remarks

Exploring rational behavior is of paramount significance in decision theory and game theory.The theory of subjective expected utility has often been regarded as a standard approach to single-agent decision making under uncertainty,and it accounts for individual rationality in terms of maximizing expected utility with respect to subjective probability representing decision makers’beliefs about states of the world.Evidently,in strategic games ascribing an “irrational”belief to a rational player would render the player’s behavior indistinguishable from that of a genuinely irrational player.It thus suggests that the players’beliefs may play an important role in determining rational behavior.

In this paper we have examined the traditional approach to strategic interactions and the standard solution concepts Nash equilibrium.We have demonstrated that the traditional approach does not resemble the basic idea of the orthodox decision theory,and Nash equilibrium cannot be derived from the more primitive decision-theoretic principle that accounts for individual rationality.We do not deny that the traditional approach to games has provided interesting intuitions and important applications to economic theory.We maintain,however,that a more decision-theoretic approach to strategic interactions may provide valuable insights into the understanding of interactive rationality by introducing subjective probabilities to represent players’beliefs regarding their opponents’strategy choices.

In particular,we hope to have convincingly shown that the concept of rationalizability does provide a general game-theoretic framework that is in the vein of a decision-theoretic approach to strategic situations.Roughly speaking,the solution concept called rationalizability admits the subjective probability representation of players’beliefs,and requires the players to model each other as expected utility maximizer with respect to subjective beliefs,which assign positive probabilities only to rational actions.In this sense,the concept of rationalizability takes a view of rational behavior in strategic situations that is very much decision-theoretic in spirit.

[1]R.J.Aumann,1976,“Agreeing to disagree”,Annals of Statistics,4(6):1236-1239.

[2]R.J.Aumann,1987,“CorrelatedequilibriumasanexpressionofBayesianrationality”,Econometrica,55(1):1-18.

[3]R.J.Aumann,1995,“Backward induction and common knowledge of rationality”,Games and Economic Behavior,8(1):6-19.

[4]D.Bernheim,1984,“Rationalizable strategic behaviour”,Econometrica,52(4):1007-1028.

[5]D.Bernheim,1985,“Axiomatic characterizations of rational choice in strategic environments”,Scandinavian Journal of Economics,88(3):473-488.

[6]C.Bicchieri,1989,“Self refuting theories of strategic interaction:A paradox of common knowledge”,Erkenntnis,30(1):69-85.

[7]K.BinmoreandA.Brandenburger,1988,CommonKnowledgeandGameTheory,Discussion Paper 167,London School of Economics.

[8]A.Brandenburger,1992,“Knowledge and equilibrium in games”,The Journal of Economic Perspectives,6(4):83-101.

[9]A.Brandenburger and E.Dekel,1987,“Rationalizability and correlated equilibria”,Econometrica,55(6):1391-1402.

[10]J.C.Harsanyi,1977,Rational Behavior and Bargaining Equilibrium in Games and Social Situations,Cambridge:Cambridge University Press.

[11]J.C.Harsanyi,1982,“Subjective probability and the theory of games:Comments on Kadane and Larkey’s paper and rejoinder to professors Kadane and Larkey”,Management Science,28(2):120-124,124-125.

[12]J.B.Kadane and R.D.Larkey,1982,“Subjective probability and the theory of games and reply to professor Harsanyi”,Management Science,28(2):113-120 and 124.

[13]D.Lewis,1969,Convention:A Philosophical Study,Cambridge,Massachusetts:Harvard University Press.

[14]D.R.Luce and H.Raiffa,1957,Games and Decisions:Introduction and Critical Survey,New York:Wiley.

[15]R.D.McKelvey and T.R.Palfrey,1992,“An experimental study of the centipede game”,Econometrica,60(4):803-836.

[16]R.B.Myerson,1991,Game Theory:Analysis of Conflict,Cambridge,Massachusetts:Harvard University Press.

[17]R.F.Nau and K.F.McCardle,1990,“Coherent behaviour in noncooperative games”,Journal of Economic Theory,50(2):424-444.

[18]J.vonNeumannandO.Morgenstern,1944,TheoryofGamesandEconomicBehavior,Princeton:Princeton University Press.

[19]M.J.Osborne and A.Rubinstein,1994,A Course in Game Theory,Cambridge,Massachusetts:MIT Press.

[20]D.Pearce,1984,“Rationalizable strategic behaviour and the problem of perfection”,Econometrica,52(4):1029-1050.

[21]P.Reny,1992,“Rationality in extensive form games”,Journal of Economic Perspectives,6(4):103-118.

[22]R.W.Rosenthal,1981,“Games of perfect information,predatory pricing and the chain-store paradox”,Journal of Economic Theory,25(1):92-100.

[23]L.J.Savage,1954,The Foundations of Statistics,New York:John Wiley and Sons.

[24]R.Stalnaker,1996,“Knowledge,belief and counterfactual reasoning in games”,Economics and Philosophy,12(2):133-163.

[25]J.C.C.Tan and S.R.C.Werlang,1988,“The Bayesian foundations of solution concepts in games”,Journal of Economic Theory,45(2):370-391.