郝兆宽

复旦大学哲学学院

zkhao@fudan.edu.cn

杨跃

新加坡国立大学数学系

matyangy@nus.edu.sg

本文打算讨论这样的一个问题：哥德尔所坚持的柏拉图主义如何影响着在他之后的数学基础研究，特别是集合论的研究。一方面，将柏拉图主义作为工作假设在很大程度上影响了集合论发展的走向，另一方面，这些研究的一些出人意料而又极具意义的重大进展又在一定程度上为柏拉图主义做出了有力的辩护。哲学和数学之间这样显明的关联是不多见的，在我们看来对这类关联的研究是数学哲学中最有意义的课题之一。

在讨论正题之前，针对数学中的柏拉图主义和数学哲学研究的方法论问题，我们想先谈一点看法，因为在现有的数学哲学研究中，大家的出发点和研究问题方式是很不相同的。

首先，本文不打算就哥德尔本人的强实在论立场作深入的讨论。哥德尔的柏拉图主义，在他1944年的“罗素的数理逻辑”（[2]）中就有所显示。在罗素篇中，哥德尔引用了罗素将逻辑学与自然科学在本体论上的类比，“逻辑学一如动物学，它研究实在的世界，不过是研究其更抽象、更一般的特点而已”（[6]）；提到在认识论上的类比，逻辑和数学的公理不必非得具有自在的显明性不可，而是可以从如下事实获得核证，它们的后承与数学史的发展中被发现为自明的东西相符合。哥德尔评论道：“这个观点已然大体上为后续的发展所核证，而将来可望获得更多的核证”。近些年集合论的发展，似乎为哥德尔的预言做了进一步的核证。如同罗素（早期的）这种实在论观点一样，我们认为对科学这个概念不能仅仅理解为实验科学或自然科学，而是要把数学这样的以抽象概念为研究对象的科学包括在内。因此，数学哲学与物理学哲学和生物学哲学一样，是科学哲学这一大类中的一员，而不是分析哲学或者其他什么哲学的一个分支。

在方法论上，仅靠分析数学的语言只能把握数学思想（或是数学哲学思想）很小的一部分；而且通常是在该数学领域发展成熟之后才可以进行。元语言和对象语言的划分特别能说明这一点。虽然，理论上我们在数学中可以使用严格化的形式语言作为对象语言，但是却不可能有完全形式化的元语言。当我们对形式化的数学做分析时，工作于其中的元理论是非形式化的，这个元理论的边界十分模糊。虽然有哲学家认为元理论包含了严格有穷的数学，但没有证据表明，严格有穷的数学就是数学的全部。即便是在形式系统内部，数学家的工作也不是借助推理的规则推演出那些定理。更多的情况是通过对数学世界的某种直观或认知，猜想或者断言某些事实是真的，然后再以证明的方式去验证。本文涉及的集合论中的一些最新的进展特别表明了这一点。

在方法论的另一方面，我们认为把数学实践统统归结到大脑神经元的活动对数学哲学的研究作用不大。就像物理学哲学不会把物理学家的大脑作为研究对象一样，分析数学家的大脑也无助于数学真理的获得。有众多的哲学理论试图将数学语言中有关数学对象，特别是无穷对象的存在断言进行重新解释，使其本质上成为谈论某些有穷的物理对象，如符号，或大脑内部某种状态的言语。但是，迄今为止，没有任何哲学理论能如其声称的那样完成这种解释。尽管我们相信脑科学的发展会对数学哲学产生根本性的影响，但今天的脑科学知识距离分析人的思维活动还差得很远。现在就期待脑神经科学家来给数学哲学问题提供答案是对问题的过度简化。在这种简化下，人类的所有思维，无论是物理学、数学还是文学都（在当今的科技条件下）毫无区别。一种健全的数学哲学最起码要与数学实践密切相关，否则只能成为文字游戏。

抱着这样的信念，我们就不可避免地要密切关注当代数学的进展。任何有关哲学的论断，都要尽可能地在已有或正在取得的数学成果中寻找相关的“证据”。这里的情形可以与物理学哲学做一个比较。一大部分的物理学哲学研究，如果不是全部的话，与近百年来物理学在一些基础问题上的重要理论和进展密切相关。但正如科纳（P.Koellner）所指出的，数学哲学中绝大多数工作却相反，它们与当代数学的发展几乎毫无关系。（[5]）造成这种局面的原因十分复杂，不属于本文讨论的范围。但是，十分确定的是：加强这个方向的研究，保持数学哲学与数学的最新进展的密切联系，应该能期待巨大的收获。当然，这也不可避免地使得这类数学哲学研究更为数学化。

最后，文章中的数学定义和定理，从某种意义上，是我们为论证而搜集的证据。借助这些定理，读者可以更好地把握概念间的关系，大致看出当今集合论发展的脉络，从而体会出其中的哲学意蕴。

1 独立性现象与数学真理

集合论中充满了独立性现象。在这些现象背后的是有关集合论真理的哲学问题，即：

一个集合论语言中的语句σ是真的，这是什么意思？

有一派观点认为σ是真的当且仅当σ在ZFC中可证。

我的感觉是，除了那些一致性命题，ZFC穷尽了我们的直观，所以，证明意味着在ZFC内证明。（[7]，第3页）

而这就意味着那些独立于ZFC的语句没有真假可言。

这是一个有重大影响的选择。其中最重要的影响就是承认CH本身是无意义的，而CH也许是我们对不可数集合所能提出的第一个重要问题。（[1]，第13页）

这样的立场被称为“形式主义”。与之相对应的立场是“柏拉图主义”，它认为一个集合论语句为真当且仅当它描述了集合宇宙中的一个客观事实。独立性命题产生的原因是我们对客观数学世界的认识不够完备。但这不意味着这些命题本身是没有真假的无意义命题，相反随着对集合宇宙认识的不断深入，我们最终会决定它们的真假。

……基于此处采取的立场，从已接受的集合论公理出发，一个有关康托猜想的不可判定性的证明（与一个对π的超越性的证明完全不同）决不是问题的解决。……集合论概念和定理描述了一个完全确定的实在，在其中康托猜想一定是或真或假。因此，源于今天已接受公理的对它的不可判定性，只能意味着这些公理没有完备地描述那个实在。这一信念绝非空想，因为有可能指出一些方向，在其中能得到对一些问题的判定，而这些问题对于通常的公理是不可判定的。（[4]，第260页）

把所有独立于ZFC的命题都看作无意义的，这种观点有一个困难就是这些命题在认识论地位上不是完全等价的。例如，有人认为CH无意义，因为“任意实数的子集”这个概念模糊不清。但是，几乎不会有人认为“所有投影集都是可决定的（PD）”无意义，因为这其中并不涉及“任意实数子集”的概念，而只是谈论了投影集这样的具体可定义的数学对象。但PD与CH一样，是独立于ZFC的。因此，武丁（H.Woodin）向形式主义提出了如下挑战：

……（形式主义）这种立场要站得住脚，那就或者集合论中类似的不可解问题也必须被看作是无意义的，或者必须解释为什么连续统假设的问题是与那些问题不同的。我指的是那些描述集合论的经典问题，它们在连续统假设提出不久也被提了出来。（[8]，第29页）

这要求人们进一步仔细分析PD与CH：

定义1.1 无穷基数δ是武丁基数当且仅当对任意函数f:δ→δ，存在初等嵌入

j:V→M，如果κ=crt(j)，则f[κ]⊆κ并且Vj(f)(κ)⊆M。我们用

表示全体武丁基数的类。

1985年武丁证明了以下定理：

定理1.2(武丁,1985)如果M是ZFC的传递模型，并且M⊨“W是真类”，则对任意M脱殊滤G，

定理1.3(马丁、斯蒂尔，1985)如果存在无穷多武丁基数，则PD成立。进而：

推论1.4对任意传递模型M，如果M⊨ZFC+“W是真类”，则对任意M脱殊滤G，都有M[G]⊨PD。

反观CH，列维（Levy）和索洛维（Solovay）1967年证明了：

定理1.5(列维、索洛维，1967)令σL为任意一条已知的大基数公理，假设M是ZFC的传递模型并且M⊨σL，则存在M脱殊滤G和H，M[G]⊨σL+CH而M[H]⊨σL+¬CH。

比较推论1.4和定理1.5，我们看到：在PD与CH之间确实存在着带有根本意义的差别。与PD不同，大基数公理对CH的独立性无能为力。这种差别是否可以帮助形式主义回应以上挑战呢？

2 多宇宙真理观与Ω猜想

我们首先将形式主义可能的回应严格描述出来，这需要一系列的定义。

定义2.1令M为ZFC的可数传递模型，则由M生成的脱殊多宇宙VM为满足以下条件的最小模型类：

1.M∈VM；

2.如果N∈VM，而N′=N[G]是N的脱殊扩张，则N′∈VM；

3.如果N∈VM，而N=N′[G]是N′的脱殊扩张，则N′∈VM。

简单说，VM是包含M并且对脱殊扩张和脱殊收缩封闭的最小模型类。由V生成的脱殊多宇宙记作V。

定义2.2(脱殊多宇宙的真)对任意ZFC的可数传递模型M，和对任意集合论语言中的语句σ，我们称

·σ是M-脱殊多宇宙真的，当且仅当它在VM的每个模型中都真，记作VM⊨σ；

·σ是M-脱殊多宇宙假的当且仅当VM⊨¬σ；

·σ是M-脱殊多宇宙无意义的当且仅当VM/⊨σ并且VM/⊨¬σ。

特别地，如果σ在由V生成的脱殊多宇宙中为真，则称σ是脱殊多宇宙真的，记作V⊨σ。其他概念类似。

根据推论1.4，如果VM的每个模型都满足“W是真类”，则PD是M脱殊多宇宙真的；根据定理1.5，对任意M，CH都是脱殊多宇宙无意义的。这看起来使得脱殊多宇宙立场比形式主义更精致，也更合理。似乎也在一定程度上回应了武丁的挑战。但是，武丁又通过一系列的数学工作论证了脱殊多宇宙立场难以成立，这需要定义武丁的Ω逻辑以及Ω猜想。

回忆一下，对任给结构A，A的理论定义为：

仿此，我们定义任意结构A在脱殊多宇宙真理观下的理论为：

对任意语句σ，形如“对任意无穷序数α，Vα⊨σ”的断言是Π2断言。事实上，脱殊多宇宙的真理概念只适用于Π2语句，这是因为我们在定义脱殊多宇宙真理概念时只允许使用集合力迫。令δ0是最小的武丁基数，则H(δ+0)⊨σ和H(δ+0)/⊨σ都是Π2断言。因此，如果令

为所有Π2多宇宙真语句的集合，则在集合MΠ2中是递归的。但是，仿照塔斯基的真理不可定义性，相反的方向应该不能成立，人们把它总结成：

第一多宇宙定律所有Π2多宇宙真语句的集合MΠ2在的脱殊多宇宙理论中不是递归的。

这一定律要求不能把整个集合宇宙中的所有Π2真理，更不必说所有真理，归结

称一个集合Y⊆Vω是借助多宇宙在中可定义的，如果Y在多宇宙模型类的每个模型中都是在中可定义的。出于同样的哲学考量，还可以有：

第二多宇宙定律所有Π2多宇宙真语句的集合MΠ2不是借助多宇宙能在中可定义的。如果脱殊多宇宙的真理观不能满足以上两条定律，那它与形式主义在根本哲学立场上就是一致的，即:

把整个集合宇宙的真归结为这个宇宙的某个清晰片段的真。

形式主义者把集合宇宙的真理归结为ZFC的定理，也就是归结为数论中的真，而脱殊多宇宙立场则是把集合宇宙的（Π2）真理归结为全体基数不超过最小武丁基数的集合。哥德尔借用他的不完全性定理，曾对形式主义的这一立场做过令人信服的反对。[3]）而武丁则同样令人信服地证明，以上形式的脱殊多宇宙立场必然违反这两个定律，所以与形式主义的真理观并无根本差别。

定义2.3(武丁，1999)假设T是集合论语言中的可数理论，σ是集合论语言中的语句，我们定义σ是T的Ω-逻辑后承，记作T⊨Ωσ，当且仅当对任意完全布尔代数B，对任意序数α，如果则

定理2.4(武丁，1999)假设W是真类，并且假设T是可数理论，σ是语句，则对任意完全布尔代数B，

这就是说，假设存在武丁基数的真类，Ω-逻辑后承关系是脱殊绝对的。特别地，全体Ω-逻辑有效式的集合VΩ={σ|⊨Ωσ}不能被任何力迫改变。

还注意到，假设W是真类，则MΠ2与VΩ具有同样的图灵复杂度，即，每个集合都在另一个集合中是递归的。同样，假设W是真类，则集合恰好就是

为了定义Ω逻辑的证明，我们需要回忆一些概念。一个拓扑空间是紧致的当且仅当它的任意覆盖都有有穷子覆盖；它是豪斯道夫（Hausdorff）空间当且仅当它的任意两个不同点都有不相交的邻域。令S为紧致的豪斯道夫空间，称X⊆S在S中有贝尔性质当且仅当存在开集O⊆S使得对称差X△O在S中是贫乏集（meager set）。

定义2.5(冯琦、麦基道、武丁，1992)一个实数的子集A具有通用贝尔性质当且仅当对任意紧致豪斯道夫空间S，任意连续映射f:S→R，A在S下的原象具有贝尔性质。

定义2.6(武丁，1999)假设A⊂R具有通用贝尔性质，M是ZFC的传递模型。称M是强A-封闭的当且仅当对任意N，如果N是传递的且是M的脱殊扩张，则A∩N∈N。

定义2.7(武丁，1999)假设W是真类。假设T是可数理论，σ是语句，则T⊢Ωσ当且仅当存在A⊂R：

1.A是通用贝尔集；

2.对任意可数传递模型M，若M是强A-封闭的且T∈M，则M⊨“T⊨Ωσ”。

定理2.8(武丁，1999)假设W是真类，并且假设T是可数理论，σ是语句，则对任意完全布尔代数B，

定理2.9(武丁，1999)假设W是真类。如果T⊢Ωσ，则T⊨Ωσ。

Ω猜想假设W是真类。对任意语句σ，⊨Ωσ当且仅当⊢Ωσ。

叙述了什么是Ω猜想，我们就可以回到武丁的回应上了：

定理2.10假设W是真类且Ω猜想成立，则VΩ在集合VΩ(H(δ+0))中是递归的。

根绝前面的分析，这实际上是说脱殊多宇宙立场违反了第一多宇宙定律。而下面的定理则是说，这一立场同样违反第二多宇宙定律。

定理2.11假设W是真类并且Ω猜想成立，则VΩ在集合H(δ+0)中可定义。

所以，脱殊多宇宙真理观不过是一种更为精致的形式主义。当然，这种站在柏拉图主义立场上的挑战要依赖于Ω猜想的成立与否。接下来我们讨论一些更新的进展，它们似乎在某种意义上暗示这个猜想是真的。

3 终极L理论

Ω猜想如果不成立，那一定是因为某个大基数公理，而且这个大基数公理超出了现有内模型计划。所谓“内模型计划”指的是构造一个类似于L的模型，在其中某个大基数公理成立。这项研究计划的动机源自于斯科特（D.Scott）的以下定理：

定理3.1(斯科特，1961)假设存在一个可测基数，则V/=L。

也就是说，哥德尔的L不能容纳可测基数，当然也不能容纳更大的基数。所以，这样的问题自然就被提了出来：

是否存在一个类似于L的模型，它能容纳可测基数或更大的基数？

很快，库能（K.Kunen）证明了

定理3.2(库能，1970)假设U是κ上的κ完全的正则非主超滤，则在L[U]中，κ是一个可测基数，并且是唯一的可测基数。

这实际地开启了内模型的研究计划，并且在随后的年代里，这个计划取得了相当的成功。目前人们已经能够构造可以容纳强基数的内模型。

但是，Ω猜想与已有的具有内模型的大基数都是相容的，所以要证明它不成立，我们需要容纳更大无穷的内模型。不唯如此，能证明Ω猜想不成立的大基数公理一定在大基数层谱中处于一个十分关键的位置，这一位置必定会有“来自内模型理论的证据”。（参见[9]）

另一方面，如果Ω猜想在所有已知的大基数公理下都成立，那就是Ω猜想在V中成立的强烈依据。而武丁有关终极L的研究表明，所有的证据都显示，没有任何已知的大基数公理会否证Ω猜想。我们以下简述这一重要的思想。（在以下的讨论中，所有未注明的定理和定义都属于武丁。）

如果存在可测基数，则V/=L，所以L虽然具有很好的结构性质，并且V=L可以解决包括CH在内的独立性问题，但它不可能是新公理的候选，L与V相差太远了。库能的L[U]可以容纳可测基数，在这个意义上比L更接近V。但是，L[U]中只有一个可测基数，它甚至不能容纳第二个可测基数，更不必说更大的基数了。所以，最终的任务就成了构造一个可以容纳所有大基数的类L结构，人们将这样的结构称为“终极L”。这看起来是不能完成的任务，因为在构造容纳大基数的内模型的过程中，人们发现每向上一步，都只能得到仅仅包含一个相应大基数的模型，要想容纳所有的大基数，我们有无穷多个内模型需要构造。但是，武丁的一个重要发现彻底改变了这种情形，这又需要一些新的数学定义：

定义3.3假设N是一个ZFC的模型，δ是一个超紧基数，如果对任意λ＞δ，存在Pδ(λ)一个δ-完全的正则精良超滤U满足：

(1)Pδ(λ)∩N∈U；

(2)U∩N∈N，

就称N是关于δ是超紧基数的弱扩张子模型（weak extender model）。

弱扩张子模型之所以重要，是因为它有我们需要的性质。首先，它十分接近V。就我们目前的问题而言，这意味着它有正确的基数概念。

定理3.4假设N是关于δ是超紧基数的弱扩张子模型，并且在N中，λ＞δ是正则基数，则在V中，cf(λ)=|λ|。特别地，如果λ在V中依然是基数，则它在V中是正则的。

推论3.5假设N是关于δ是超紧基数的弱扩张子模型，并且在V中，γ＞δ是奇异基数，则

(1)λ在N中是奇异基数；

(2)(γ+)N=γ+，即N能正确地计算奇异基数的后继。

不仅如此，与以往的内模型不同，弱扩张子模型可以容纳任意多的可测基数。

推论3.6假设N是关于δ是超紧基数的弱扩张子模型，并且在V中，κ＞δ是奇异基数，则κ在N中是可测基数。

事实上，弱扩张子模型可以容纳δ以上的所有大基数！

定理3.7(普遍性)假设N是关于δ是超紧基数的弱扩张子模型，并且在V中，γ＞δ是正则基数，并且

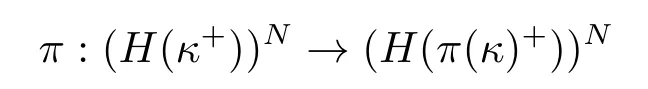
是一个初等嵌入，并且crt(π)＞δ，则π∈N。

也就是说，V中δ以上的大基数都在N中保持为δ以上的大基数。这不能不说是一个令人惊奇的结果。

但是，弱扩张子模型是否存在呢？到目前为止它只是一个抽象的概念。但有一些数学“证据”暗示其存在。

定理3.8(詹森，1974)L或者非常接近V或者离V很远。即以下二者必居其一：

(1)对任意V中的奇异基数γ，γ在L中是奇异基数，并且(γ+)L=γ+；（L非常接近V。）

(2)每个不可数基数在L中都是不可达的。（L与V相差很远。）

武丁则得到了关于HOD的类似结果。

定理3.9假设κ是可扩张基数，则HOD或者非常接近V，或者（在κ以上）离V很远。即以下二者必居其一：

(1)对任意V中的奇异基数γ，γ在HOD中是奇异基数，并且(γ+)HOD=γ+；

(2)所有大于κ的正则基数在HOD中都是ω-强可测基数。

假设存在可扩张基数，则无论哪种情况成立，HOD中都存在一个可测基数。因为如果(1)成立，则HOD是κ是超紧基数的弱扩张子模型，κ显然是HOD中的可测基数。而如果(2)成立，则更是显然。

HOD猜想HOD接近V，或者说，在ZFC内可以证明：在HOD中，{δ|δ是正则基数

但不是ω-可测基数}是一个真类。

如果HOD猜想成立，则HOD是一个弱扩张子模型，反之亦然。

定理3.10假设κ是一个可扩张基数，则以下命题等价：

1.HOD猜想成立；

2.HOD是κ是超紧基数的弱扩张子模型。

那么，HOD猜想是否成立呢？它会不会像CH本身一样是独立的呢？从目前的证据来看，这似乎不可能。因为武丁证明，HOD猜想是脱殊绝对的：如果HOD猜想在V中成立，则它在V的所有脱殊扩张中都成立。所以不可能用力迫法证明HOD猜想的独立性，而力迫法又几乎是唯一证明独立性的手段。

还有一些支持HOD猜想的证据，目前已经知道的是以下这点与ZFC一致：ω1和ω2在HOD中是ω-强可测基数。但是，我们甚至不知道HOD中是否能够容纳4个ω-强可测的正则基数；也不知道对任意奇异基数γ，γ+是否是HOD中的ω-强可测基数；更不知道是否存在超紧基数以上的ω-强可测的正则基数。

如果HOD猜想成立，则HOD包含了一个弱扩张子模型，而这样的模型可容纳所有已知的大基数，因此是某种意义上的“终极L”模型。武丁还提出了这样一种设想，即，在不知道如何构造“终极L”的情况下，我们仍可以叙述公理：“V=终极L”。

V=终极L公理公理“V=终极L”包括以下命题：

(1)存在武丁基数的真类W；

(2)对任意Σ3-语句φ，若φ在V中成立，则存在一个通用贝尔集A⊆R，使得

终极L猜想假设κ是可扩张基数，则存在模型N满足：

(1)N是κ是超紧基数的弱扩张子模型；

(2)N⊆HOD；

(3)N|=“V=终极L”。

定理3.11假设终极L猜想成立，则：

1.CH成立；

2.V=HOD；

3.Ω猜想成立。

这样，我们可以合理地认为，如果终极L猜想成立，那它一定会在两个方向上为数学中的柏拉图主义辩护。首先，它证明Ω猜想成立，而根据第二节的分析，这从根本上拒绝了多宇宙的真理观。因为，在Ω猜想成立的情况下，脱殊多宇宙真就可归结为中的真，这本质上与形式主义将真归结为在ZFC中可证是一样的。正如我们已经指出的，这种对真理的看法无法说明这样的问题：为何一些独立性命题是无意义的而另一些不是？

其次，如果终极L存在，那ZFC的众多模型中就有一个非常特殊的。它不仅可以容纳所有已知的大基数，而且具有很好的结构性质从而解决所有的自然的独立性问题。同时，在“终极L中为真”对于集合力迫又是免疫的，从而不能用通常的力迫证明其独立性。终极L的这种特殊性自然需要哲学上的解释。武丁多次强调，这种特殊性源自它十分接近V，那个真实的集合论宇宙。除了这种柏拉图主义的解释，我们暂时看不到任何其他的哲学立场能够做到这一点。

[1]P.Cohen,1970,“Commentsonthefoundationsofsettheory”,inD.Scott(ed.),AxiomaticSetTheory,pp.9-16,Proceedings of the Symposiumin Pure Mathematicsofthe AmericanMathematical Society.

[2]K.Gödel,1990,“Russell’s mathematical logic”,Collected Works,II:264-270.

[3]K.Gödel,1990,“Some basic theorems on the foundation of mathematics and their implications”,Collected Works,II:304-323.

[4]K.Gödel,1990,“What is Cantor’s continuum problem?”,Collected Works,II:264-270.

[5]P.Koellner and H.Woodin,Foundation of Set Theory:The Search for New Axioms,preprint.

[6]B.Russell,1919,Introduction to Mathematical Philosophy,London:Allen and Unwin.

[7]S.Shelah,1993,“The future of set theory”,in H.Judah(ed.),Set Theory of Reals,pp.1-12.

[8]W.H.Woodin,2004,“Set theory after russell:The journey back to Eden”,in G.Link(ed.),pp.29-48.

[9]W.H.Woodin,2010,“The continuum hypothesis,the generic-multiverse of sets,and the Ω conjecture”,in J.Kennedy and R.Kossak(eds.),Set Theory,Arithmetic and Foundations of Mathematics:Theorems,Philosophies,pp.13-42.