张新春

判断一个数能否被另一个数整除，最自然的办法就是作除法。但对于一些特殊的数，我们可以研究一些特别的判断方法。

小学数学教材中研究了2、5、3的倍数的特征。结论为：

（1）个位上是0、2、4、6、8的数，能被2整除；

（2）个位上是0、5的数，能被5整除；

（3）各個数位上的数字之和能被3整除，这个数就能被3整除。

我们先来讨论结论（1）和结论（2），这两个结论可以概括地表达为：个位上的数字能被2或5整除，这个数就能被2或5整除。

事实上，对任意自然数N，都可以写成N=10k+ b的形式，其中k逸0，0≤b≤9。这里的b就是N的个位数字。

显然，由10=5×2知10能被2和5整除，从而10k能被2和5整除。于是，只要b能被2或5整除，N=10k+b就能被2或5整除。也就是说，看一个数能否被2或5整除，只需要看个位即可。

小学数学教材中，能被2整除的数的特征和能被5整除的数的特征通常是独立安排的。在教学中，我们可以通过实例，让学生体会这两个结论的统一性。如果在课堂中通过观察、猜测、验证、归纳等活动可以让学生知道能被2或5整除的数的特征“是什么”的话，对这种统一性的体会就是关注“为什么”。

对数学问题有某种程度的敏感的读者，应该注意到10=5×2对于上述结论的重要性。同时，会马上想到另外一个等式：100=25×4。这个等式是否告诉我们，要看一个数能否被4或25整除，只要看后两位即可呢？事实正好如此。写出一般的证明并不难，我们在此只举一个例子。比如，1784=17×100+84，由于100能被4整除，所以17×100当然能被4整除，又因为84也能被4整除，于是可以作出结论：1784能被4整除。但由于17×100能被25整除，而84不能被25整除，所以1784就不能被25整除。

此时，我们一定会想到另一个等式：1000=125×8，同时知道，看一个数能否被8或125整除，只需看后三位即可。

从上面几个例子可以看出，我们要判断一个数a（比如1784）能否被另一个数b（比如4）整除，做法是从中分离出能被整除的一部分（比如1700），这时只要看剩下的部分（如84）能否被4整除就可以了。

上述第（3）个结论中，关于能被3整除的数的特征，即可以根据这个思路得到。

显然，对于10、100、1000、……这些计数单位来说，只要从中拿出1，剩下的部分9、99、999、……就都能被3整除了。于是，对于521来说，有

521=5×100+2×10+1

=（5×99+5）+（2×9+2）+1

=（5×99+2×9）+（5+2+1）

上述算式中，5×99+2×9显然能被3整除，这样一来，521能否被3整除，就取决于5+2+1能否被3整除。一般地，一个数能否被3整除，只要看各个数位上的数字之和能否被3整除。

将这个过程稍作加工，就可以构成一个在小学数学课堂中研究能被3整除的数的特征的方式。与能被2、5整除的数的特征不同，能被3整除的数的特征仅靠观察较难发现，因此，研究如何在课堂中引导学生理解能被3整除的数的特征就显得尤其重要。

由于9、99、999、……同样都能被9整除，因此，一个数能否被9整除，也只需看各个数位上的数字之和能否被9整除。

我们再来看一个稍复杂的例子。

1001=7×11×13，说明1001能同时被7、11、13整除。

下面来考察80234这个数能否被7、11、13整除。

80234=80×1000+234

=80×1001+（234-80）

由于1001能同时被7、11、13整除，所以80×1001肯定能同时被7、11、13整除。于是，要看80234能否被7、11、13整除，就只要看234-80能否被7、11、13整除了。而234-80=154=7×11×2，因此，80234能被7、11整除，但不能被13整除。据此，我们可以概括出能被7、11、13整除的数的特征（留给读者作个练习。计算过程中，可能会碰到要处理负数的情况）。

其他很多关于判断一个数能否被另一个数整除的方法，大体上都可以用这种“分离一部分显然能整除的，再看另一部分”的思路来理解。例如，对于整数M，记b为M的个位数字，而a是M分离个位数字后剩下的部分，于是有M=10a+b。此时，我们可以得到如下一些判断整除的方法。

（1）由于M=10a+b=11a-（a-b），而11a显然能被11整除，于是M=10a+b能否被11整除，只要看（a-b）能否被11整除即可。比如253，因为25-3=22，22能被11整除，所以253能被11整除。对于一些大数来说，可以反复利用这个方法。

（2）由于M=10a+b=13a+13b-3（a+4b），要判断M能否被13整除，只要看（a+4b）能否被13整除即可。比如273，27+4×3=39，能被13整除，所以原数273也能被13整除。同样，如果必要，这个方法也可以反复运用。

（3）由于M=10a+b=17a-34b-7（a-5b），17a-34b能被17整除，要判断M能否被17整除，只要看（a-5b）能否被17整除即可。比如357，35-7×5=0，能被17整除，所以原数357也能被17整除。同样，如果必要，这个方法也可以反复运用。

理解了这一点，我们甚至可以自己创造出一些判断一个数能否被另一个数整除的方法。值得说明的是，以上这些方法有一个共同点：为了判断 M能否被N整除，都是通过判断一个比M小的数能否被N整除来实现。具体做法是从M中分离出一部分，使这一部分能被N整除，然后考察另一部分能否被N整除。即把一个整除判断的问题转化成一个更小的数的整除判断问题，后者通常比前者容易，这就使得这些判断方法有实用价值。这种思路也常常用来讨论与整除有关的问题。

例：证明不存在这样的整数n，使得n2+n+2011能被2010整除。

证明：假设存在这样的整数n，使得n2+n+2011能被2010整除，则有整数m，使得n2+n+2011=2010m，即n2+n+1=2010（m-1）。于是n2+n+1能被2010整除，而2010能被5整除，于是n2+n+1应能被5整除。

但对于任意的整数n，只能有以下5种情况：5t，5t+1，5t+2，5t+3，5t+4。

当n=5t时，n2+n+1=（5t）2+5t+1=5（5t2+t）+1，显然不能被5整除。（注：这里即把n2+n+1分成两部分，其中一部分能被5整除，而另一部分不能，从而说明n2+n+1不能被5整除）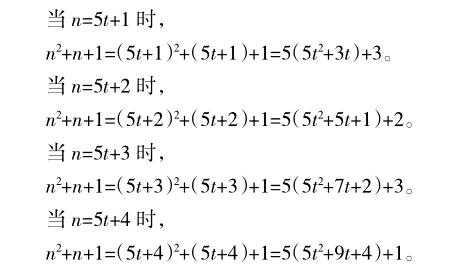

n2+n+1都不能被5整除。因此，对于任意的整数n，n2+n+1都不能被5整除，从而不能被2010整除，这就证明了使得n2+n+2011能被2010整除的整数n是不存在的。