基于差分插补原理的平面三次多项式曲线插补*
2017-07-31王宏甲杨召彬赵庆志张林华
乔 磊,王宏甲,杨召彬,赵庆志,张林华
(1.山东理工大学 机械工程学院,山东 淄博 255000;2.山东新华医药器械股份有限公司, 山东 淄博 255086)
基于差分插补原理的平面三次多项式曲线插补*
乔 磊1,王宏甲1,杨召彬1,赵庆志1,张林华2
(1.山东理工大学 机械工程学院,山东 淄博 255000;2.山东新华医药器械股份有限公司, 山东 淄博 255086)
针对经济型数控系统中平面三次多项式曲线的插补,提出采用差分插补原理对其进行直接插补。该方法插补精度较高,插补误差不会超过1/2个脉冲当量。通过定义三次多项式曲线的ISO代码,以及对差分插补原理中相关概念的分析,得到了三次多项式曲线的差分插补代码,简化了加工程序的编制,降低了数控系统的译码负担。针对两种类型的三次多项式差分插补代码的计算,进行了详细的译码分析。结合VC++6.0开发了数控仿真程序,并在教学用三坐标数控实验台上进行了插补测试,验证了针对差分插补代码译码方法的正确性,实现了三次多项式曲线的直接插补。
数控系统;差分插补原理;三次多项式曲线;ISO代码
0 引言
插补运算是整个数控系统的核心,插补精度直接影响到数控系统的加工质量[1]。传统的经济型数控系统中只有直线、圆弧插补算法,无法应对工程中广泛应用的三次样条曲线的插补。
三次样条曲线是分段三次多项式函数,要求在各段的衔接点上有二阶连续的导数,从而保证曲线的光滑性。对于高次曲线的加工,在经济型数控系统中,通常采用CAD/CAM软件自动编程。为实现加工精度的要求,编程软件需要产生大量的微小直线段或圆弧,再由数控系统进行译码与插补等处理[2-4]。这种方法存在数据处理负荷大,频繁加减速导致的进给率不连续以及加工效率低等不足。在高速、高精度的现代化加工中,直线插补与圆弧插补的不足越来越明显,已经不能满足现代化的加工要求[5]。
本文采用的差分插补原理[6],其插补方法具有插补功能强大,控制精度高,操作使用容易等优点。该插补方法理论上可以插补任意正高次曲线。在相关文献[7-10]中,对直线以及常见的二次曲线的差分插补进行了研究,本文将针对三次多项式曲线的插补进行研究。通过定义三次多项式曲线的ISO代码,并将其转化为差分插补代码,实现三次多项式曲线的直接插补。
1 差分插补原理中的相关概念与定义
1.1 差分插补原理的依据与各坐标系的定义
根据参考文献[6-7],差分插补原理的依据是从原点开始,依据函数递增的趋势进行推导,其插补误差不会超过半个脉冲当量。在插补的过程中,为了满足插补的理论依据,建立了一系列的坐标系,各坐标系的论述如下。
(1)定义用绝对坐标系:该坐标系与通常定义的平面直角坐标系相同[11],主要用于定义曲线,为曲线的ISO代码提供与曲线函数相关的信息。
(2)相对坐标系:为了保证曲线在加工过程中满足差分插补的理论依据,曲线方程要经过坐标系平移和变向化为可分离变量的正高次曲线。此时会建立相对坐标系,保证曲线起点为坐标原点,起点处的切线在相对坐标系的第一象限。根据可分离变量的正高次曲线,求x、y的各阶差分。
(3)加工用绝对坐标系:在初始化插补参数时,L为曲线起点的切线方向所在的绝对象限号,象限的定义为L41,L42,L43以及L44。在此绝对坐标系中,x′ 轴与y′ 轴的正方向是根据机床进给的正方向选取的。故将其命名为加工用绝对坐标系,为机床各轴进给方向提供基准。在本文中,取x′轴水平向右,y′轴垂直向上为正方向,选取曲线加工起点为坐标原点来建立加工用绝对坐标系。
1.2 差分插补代码的初始化
将在定义用绝对坐标系中的三次多项式曲线方程Pn(x)=Qm(y),按照坐标平移和变向化为相对坐标系中的正三次曲线方程,其形式为:
y=b3x3+b2x2+b1x
(1)
则其差分插补代码为:
jx1,jx2,jx3,jy1,F,G,jj,L
各代码含义为:
jx1:x的一阶差分,jx2:x的二阶差分,
jx3:x的三阶差分,jy1:y的一阶差分,
F:插补偏差,G:计数方向,
jj:曲线在x轴(或者y轴)上的投影叠加和,
L:加工用绝对坐标象限。
其中,jx1=b3+b2+b1,jx2=6b3+2b2,jx3=6b3,jy1=1,在插补的过程中,必须保证jx1>0,jy1>0,其具体差分计算见相关参考文献[1]。F为插补偏差,F=Pn(x)-Qm(y)或者F=Qm(y)-Pn(x),在初始化时,F=0。G为计数方向,用来判断投影方向。若曲线终点的切线斜率绝对值K>1时,G=Gy,曲线的投影方向为y轴,否则G=Gx,曲线的投影方向为x轴。jj为曲线在计数方向上的计数长度。L为曲线加工起始段所在的加工用绝对坐标系象限号。在曲线的插补过程中,当二阶差分值为负值时,有可能出现一阶差分值为负值的情况。为使插补运算正常进行,必须改变坐标轴的进给方向,保证各一阶差分值为正,所以要调整L所在的加工用绝对坐标系的象限。
2 三次多项式曲线ISO代码译成差分插补代码
参考圆弧插补的ISO代码[12],本文定义三次多项式曲线的ISO代码:
G11XxYyIiJjAaBbCc
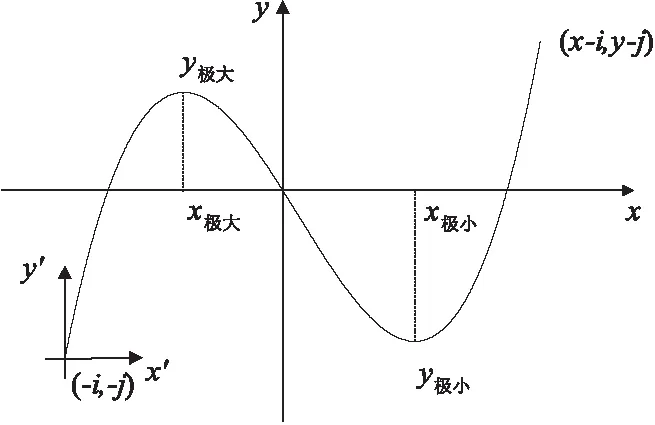
其中,x、y为三次多项式曲线终点的坐标值。在G90状态,x、y为工件坐标系中的圆弧终点坐标。在G91状态,x、y为曲线终点相对与起点的距离。在G90或者G91状态,i、j均为三次多项式曲线定义用绝对坐标系的原点相对起点的坐标。本文主要分析在G91状态,则在定义用绝对坐标系中,(-i,-j),(x-i,y-j) 分别为曲线的起点与终点坐标。a,b和c分别为三次多项式曲线方程的三次项、二次项以及一次项的系数。则三次多项式曲线的方程为:
y=ax3+bx2+cx
(2)
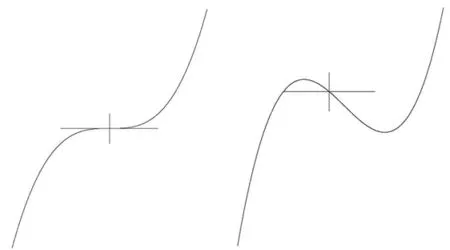
当a>0(或a<0)时,令Δ=4b2-12ac,三次多项式曲线有两种类型:
(1)当Δ≤0时,函数无极值,随x增加呈递增(递减)趋势,这种类型定义为I型三次多项式曲线(后文简称I型曲线);
(2)当Δ>0时,函数存在极值,有极大值与极小值,这种类型定义为II型三次多项式曲线(后文简称II型曲线)。
2.1I型曲线(a>0)相对坐标编程
(1)当x>0 &&y>0时,曲线起点在定义用绝对坐标系的图形如图1所示,其在相对坐标系下的正三次曲线程为:
y-j=a(x-i)3+b(x-i)2+c(x-i)
(3)
将式(3)整理为式(1)的形式:
y=ax3+(-3ai+b)x2+(3ai2-2bi+c)x
则差分插补代码:
jx1=3ai2-(3a+2b)i+a+b+c,jx2=
6a(1-i)+2b,jx3=6a,jy1=1,L=L41
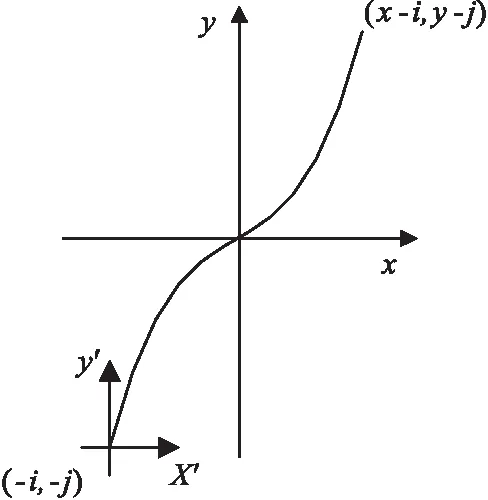
图1 I型曲线(a>0),x>0 && y>0时
对式(2)求导数值,确定计数方向和计数长度:
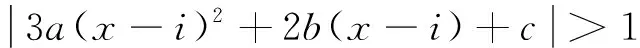
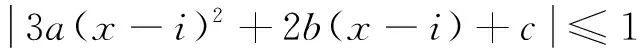
(2)当x<0&&y<0时,曲线起点在定义用绝对坐标系的图形如图2所示,其在相对坐标系下的正三次曲线程为:
-y-j=a(-x-i)3+b(-x-i)2+c(-x-i)
(4)
将式(4)整理为式(1)的形式:
y=ax3+(3ai-b)x2+(3ai2-2bi+c)x
则差分插补代码:
jx1=3ai2+(3a-2b)i+a-b+c,jx2=6a(i+1)-2b,
jx3=6a,jy1=1,L=L43
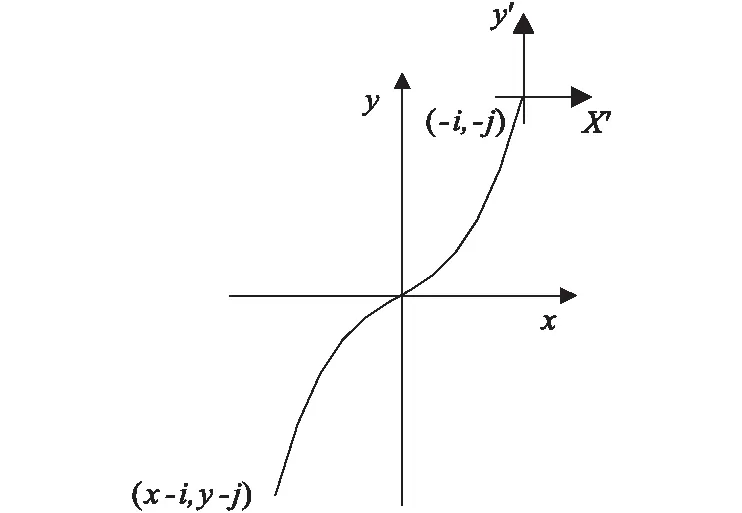
图2 I型曲线(a>0),x<0 && y<0时
对式(2)求导数值,确定计数方向和计数长度:
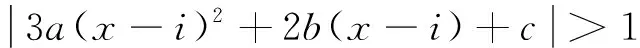
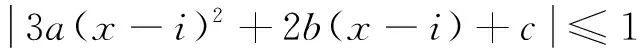
2.2II型曲线(a>0)相对坐标编程
II型曲线函数存在极值,有极大值与极小值,设函数的极值点为x极大,x极小,其相应的极值分别为y极大,y极小。
(1)当x>0 && -i y-j=a(x-i)3+b(x-i)2+c(x-i) (5) 将式(5)整理为式(1)的形式: y=ax3+(-3ai+b)x2+(3ai2-2bi+c)x 则差分插补代码: jx1=3ai2-(3a+2b)i+a+b+c,jx2= 对式(2)求导数值,确定计数方向和计数长度: 图3 II型曲线(a>0),x>0 && -i 以下分析,不再作图,方法原理一样。 (2)当x>0 &&x极大<-i -y-j=a(x-i)3+b(x-i)2+c(x-i) (6) 将式(6)整理为式(1)的形式: y=-ax3+(3ai-b)x2-(3ai2-2bi+c)x 则差分插补代码: jx1=-3ai2+(3a+2b)i-a-b-c,jx2= 对式(2)求导数值,确定计数方向和计数长度: (3)当x>0 &&x极小≤-i y-j=a(x-i)3+b(x-i)2+c(x-i) (7) 将式(7)整理为式(1)的形式: y=ax3+(-3ai+b)x2+(3ai2-2bi+c)x 则差分插补代码: jx1=3ai2-(3a+2b)i+a+b+c,jx2= 对式(2)求导数值,确定计数方向和计数长度: (4)当x<0 && -i>x极小时,曲线在相对坐标系下的正三次曲线程为: -y-j=a(-x-i)3+b(-x-i)2+c(-x-i) (8) 将式(8)整理为式(1)的形式: y=ax3+(3ai-b)x2+(3ai2-2bi+c)x 则差分插补代码: jx1=3ai2+(3a-2b)i+a-b+c,jx2= 对式(2)求导数值,确定计数方向和计数长度: (5)当x<0 &&x极大<-i≤x极小时,曲线在相对坐标系下的正三次曲线程为: y-j=a(-x-i)3+b(-x-i)2+c(-x-i) (9) 将式(9)整理为式(1)的形式: y=-ax3-(3ai-b)x2-(3ai2-2bi+c)x 则差分插补代码: jx1=-3ai2-(3a-2b)i-a+b-c,jx2= 对式(2)求导数值,确定计数方向和计数长度: (6)当x<0 &&x-i<-i≤x极大时,曲线在相对坐标系下的正三次曲线程为: -y-j=a(-x-i)3+b(-x-i)2+c(-x-i) (10) 将式(10)整理为式(1)的形式: y=ax3+(3ai-b)x2+(3ai2-2bi+c)x 则差分插补代码: jx1=3ai2+(3a-2b)i+a-b+c,jx2= 对式(2)求导数值,确定计数方向和计数长度: 2.3I型及II型曲线(a<0)相对坐标编程 当a<0时,I型及II型曲线与上述类型关于坐标轴对称,转化的方法与上述方法相同,不再赘述。 2.4 三次多项式曲线绝对坐标编程 在G90的绝对坐标系中,在进行差分插补代码翻译时,只要将绝对坐标进行相应变化。设上一次插补的终点为坐标为(x0,y0),则x=x-x0,y=y-y0,计算后带入相对坐标程序即可进行差分插补代码的计算。 为验证上述三次多项式曲线差分插补代码的正确性,本文根据差分插补原理,使用VC++6.0开发了相应的数控系统仿真系统[13],并在教学用三坐标数控实验台上进行了插补验证。其仿真曲线如图4所示,采用教学用三坐标数控实验台插补的三次多项式曲线如图5所示。 (a)I型曲线仿真 (b)II型曲线仿真图4 三次多项式曲线仿真 (a)I型曲线插补 (b) II型曲线插补图5 I型及II型曲线直接插补 上述三次多项式曲线的插补,在脉冲当量为0.001mm的数控实验台上,采用差分插补原理以及本文定义的G11加工代码直接进行插补,并且插补误差不会超过1/2个脉冲当量。在同样脉冲当量的情况下,采用MasterCAM对曲线进行拟合编程,加工代码超过两百行,而且在加工的过程中,既存在插补误差又存在拟合误差。 本文通过采用差分插补原理实现了三次多项式曲线的直接插补,丰富了经济型数控系统的插补功能。高次曲线的直接插补避免了大量数控代码的译码负担,以及频繁的加减速控制,为缓解数控加工精度与效率之间的矛盾,优化复杂曲线的拟合,奠定了良好的基础。 [1] 盖荣丽,王允森,孙一兰,等.样条曲线插补方法综述[J].小型微型计算机系统,2012,33(12):2744-2748. [2]YongT,NarayanaswamiR.AparametricInterpo-latorwithconfinedchorderrors,accelerationanddecelerationforNCmachining[J].Computer-AidedDesign,2003,35(13):1249-1259. [3] 韩式国,赵军,陈晓晓,等.数控编程技术及其典型应用研究[J]. 组合机床与自动化加工技术,2012(3):100-103. [4] 王允森, 盖荣丽, 孙一兰,等. 基于牛顿迭代法的NU-RBS曲线插补算法[J]. 组合机床与自动化加工技术, 2013(4):13-17. [5] 董海涛,潘海鸿,黄丽宇,等.一种优化的NURBS曲线插补算法[J]. 计算机集成制造系统,2014,20(9):2172- 2177. [6] 王敏. 差分插补方法及其在数控线切割机中的应用(一)[J]. 电加工,1981(4):16-22. [7] 赵庆志. 基于可重构理论的慢走丝线切割机床控制系统研究与设计[D]. 南京:南京航空航天大学,2005. [8] 赵庆志,谭培红,高振华. 抛物线ISO代码译成差分插补代码及其实现[J]. 机械设计与制造,2006(5):57- 59. [9] 刘肖,赵庆志,于光伟,等. 双曲线ISO代码译成差分插补代码及程序的实现[J]. 山东理工大学学报(自然科学版),2010,24(2):82-86. [10] 王宜龙,赵庆志,王海涛. 椭圆ISO代码译成差分插补代码及其程序的实现[J]. 机床与液压,2009,37(9):54-55,118. [11]甘志国. 平面解析几何[M]. 哈尔滨:哈尔滨工业大学出版社,2014. [12]黄国权. 数控技术[M]. 哈尔滨:哈尔滨工程大学出版社, 2013. [13]范建明, 曹锋, 刘金磊. 数控机床仿真系统研究[J].煤矿机械,2010,31(1):144-145. (编辑 李秀敏) Research on Interpolation of Planar Cubic Polynomial Curve Based on Differential Interpolation QIAO Lei1, WANG Hong-jia1, YANG Zhao-bin1, ZHAO Qing-zhi1, ZHANG Lin-hua2 (1.College of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255000, China; 2. SHINVA Medical Instrument Co., Ltd., Zibo Shandong 255086, China) The principle of difference interpolation is used to directly interpolate the cubic polynomial curve in the economic CNC system. The interpolation accuracy is high, and the interpolation error will not exceed 1/2 pulse equivalent. The difference interpolation code for the cubic polynomial curve is obtained, by defining the ISO code of the cubic polynomial curve and analyzing the related concepts in the differential interpolation principle. It is helpful to reduce the burden of NC decoding for the simplification of the program. According to the two types of the cubic polynomial curves, their interpolation codes are analyzed and calculated in detail. The numerical control simulation program was developed with VC++6.0, and the interpolation test was carried out on the three coordinate CNC experiment platform. The correctness of the decoding method is verified, and the direct interpolation of the cubic polynomial curves is realized. CNC; differential interpolation theory; cubic polynomial curve; code of ISO 1001-2265(2017)07-0097-04 10.13462/j.cnki.mmtamt.2017.07.023 2017-02-20; 2017-03-17 山东省自然科学基金资助项目(ZR2016EL13) 乔磊(1994—),男,山东临沂人,山东理工大学硕士研究生,研究方向为数控技术与装备,(E-mail)836773554@qq.com;通讯作者:赵庆志(1962—),男,山东淄博人,山东理工大学教授,博士,研究方向为数控技术与装备、机电一体化技术,(E-mail)zhaoqzme@163.com。 TH165;TG506 A
6a(1-i)+2b,jx3=6a,jy1=1,L=L41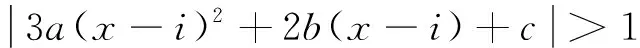
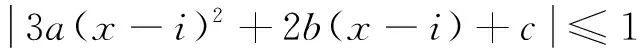
6a(i-1)-2b,jx3=6a,jy1=1,L=L44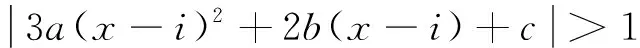
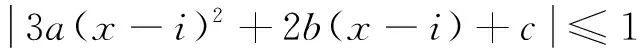
6a(1-i)+2b,jx3=6a,jy1=1,L=L41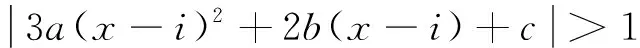
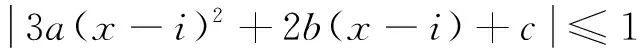
6a(1+i)-2b,jx3=6a,jy1=1,L=L43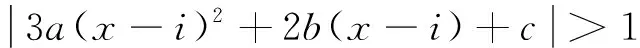
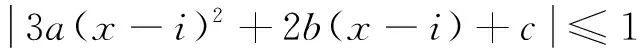
-6a(i+1)+2b,jx3=6a,jy1=1,L=L42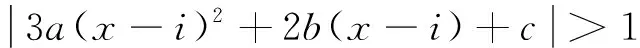
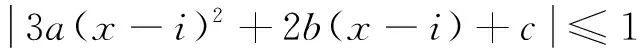
6a(1+i)-2b,jx3=6a,jy1=1,L=L43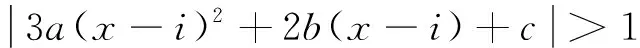
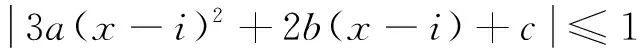
3 三次多项式曲线插补仿真与实验

4 结论
