Negative Index Materials and Their Applications:Recent Mathematics Progress
2017-07-02HoaiMinhNGUYEN
Hoai-Minh NGUYEN
(Dedicated to Haïm Brezis for his 70th birthday with esteem)
1 Introduction
Negative index materials(NIMs for short)were first investigated theoretically by Veselago[49].The existence of such materials was confirmed by Shelby,Smith and Schultz[48].The study of NIMs attracted a lot attention in the scientific community thanks to their many possible applications such as superlensing and cloaking by using complementary media,and cloaking a source via anomalous localized resonance(ALR for short).Mathematically,the study of NIMs faces two difficulties.Firstly,the equations describing the phenomena have sign changing coefficients,hence the ellipticity and the compactness are lost in general.Secondly,the localized resonance,i.e.,the field explodes in some regions and remains bounded in some others as the loss goes to 0,might appear.
In this survey,we present recent mathematics progress in understanding properties of NIMs and their applications.The following five topics are discussed:reflecting complementary media,superlensing by using complementary media,cloaking by using complementary media,cloaking a sourcevia ALR,and thelimiting absorption principle and the well-posedness of the Helmholtz equations with sign changing coefficients.The choice of these topics is related to the author’s expertise for which he made contribution in[27–33]and in his joint work with Nguyen[34–35].An interesting topic of NIMs,the construction of NIMs via various processes of homogeneization,is completely ignored;Concerning this aspect,the reader can consult[10,12,16,20,46]and references therein.
The outline of the paper is as follows.Reflecting complementary media is discussed in Section 2.To motivate this concept,we first illustrate peculiar properties of NIMs by presenting an interesting result due to Nicorovici,McPhedran and Milton[42].We then discuss its nontrivial extension in[27]via the concept of reflecting complementary media using the reflecting technique introduced there.Superlensing using complementary media is presented in Section 3.Superlensing using complementary media was suggested by Veselago[49],Nicorovici,McPhedran and Milton[42],Pendry[44–45],and Ramarkrishna and Pendry[47].Concerning this topic,we first present a class of superlensing schemes,which is a subclass of schemes given in[28],and is inspired on one hand by the suggestion of superlenses in[42,45,47]and on another hand by the study of reflecting complementary media in[27].We then provide the proof of superlensing for this class.The proof presented here uses the results in Section 2,and is simpler than the first one given in[28].Cloaking using complementary media is given in Section 4.This was suggested by Lai et al.[21].Concerning this topic,we present a cloaking scheme,which is related to[21],and the first proof of cloaking by using complementary media from[31],where the removing localized singularity technique was introduced to handle the localized resonance.This technique was inspired by the influential work of Bethuel,Brezis and Hélein on the Ginzburg Landau equation in[4].Cloaking a source via ALR is discussed in Section 5.This was discovered by Milton and Nicorovici[23]for a constant radial symmetric plasmonic structure in the two dimensional quasi-static regime.Section 5,which is based on[30],is on various properties on cloaking a source via ALR for doubly complementary media,a subclass of reflecting complementary media introduced there.As an application of these properties,one can construct a cloaking device to cloak a general source concentrate on a manifold of codimension 1 in an arbitrary medium.The limiting absorption principle and the well-posedness of the Helmholtz equations with sign changing coefficients are given in Section 6 and based on[32].Concerning this topic,we discuss various conditions on the coefficients for which the limiting absorption principle holds and the equation is well-posed.The unique solution which might not be inis obtained from the limiting absorption principle.The results presented here extend largely known results by using the integral method,the pseudo differential operator theory,and the T-coercivity approach.From Section 2 to Section 5,we mainly concentrate on the quasi-static regime in a bounded domain,even thought the results in the finite frequency regime are also mentioned.In the last section,we consider the finite frequency regime in the whole space for which the uniqueness can be established without imposing further assumptions.
2 Reflecting Complementary Media
Let 0

where,forδ≥0,2In[42],εδ is given by −1+iδ instead of−1−iδfor r 1<|x| Physically,the imaginary part ofεδis the loss of the medium.In[42],Nicorovici,McPhedran and Milton obtained,by separation of variables,the following interesting result: whereis the unique solution to the equation The surprising fact of this result is that(2.3)holds for any f with supp f∩Br3= Ø.From(2.3),one might say that the region{r2<|x| Under the condition(2.2),the property(2.3)does not hold in three dimensions,and its natural extension for the finite frequency regime is not valid in two dimensions.In[27],we extended the above results for quite general settings in two and three dimensions both in the quasistatic and the finite frequency regimes by using a completely different approach.This is given in the next two subsections.In the first one,we present an heuristic argument for(2.3),and in the second one,we discuss new results inspired from the heuristic argument. In this subsection,we assume thatasδ→ 0,and present an heuristic argument to obtain(2.3)from[27].From the assumption,is a solution to the equation Letbe the Kelvin transform with respect to∂Br2,i.e.,Define From the transmission conditions on∂Br2,we have Since F is a Kelvin transform and supp f∩Br3=Ø,it follows that where Note that F maps∂Br1into∂Br3.By the unique continuation principle,we have Letbe the Kelvin transform with respect toDefine Similar to(2.4),we have It follows from(2.5)that We also have by the property of the Kelvin transforms and the definition of u2,0.Define Sinceit follows from(2.6)–(2.7)that Therefore,we obtain(2.3). Remark 2.1If suppand suppthen,instead of(2.5),one has where w1=u1,0−u0in Br3Br2.In general,this Cauchy problem does not have a solution inor even inIn fact,one can easily see from the heuristic argument that there are two Cauchy problems in this context,another one is related to(2.7).The non-existence mentioned here is the origin of the concept of compatibility in Definition 2.2. Motivated by the heuristic argument in Subsection 2.1 and the change of variables for the Helmholtz equations(see Lemma 2.1 below),in[27],we introduced the concept of reflecting complementary media and extended(2.3)to this class.Let k≥ 0 andΩ1⊂⊂ Ω2⊂⊂ Ωbe smooth connected bounded open subsets of Rd(d=2,3).Let A be a measurable matrix-valued function andΣbe a measurable real function defined inΩ.Here and in what follows,we always assume that for a.e.x∈Ωand for some 0<Λ<+∞,and Set In[27],we were interested in the behavior of the unique solutionto the equation asδ→ 0,under the condition that(A,Σ)in Ω3Ω2is reflecting complementary to(−A,−Σ)inΩ2Ω1for someΩ2⊂⊂ Ω3⊂⊂ Ω.To motivate the definition of reflecting complementary media,let us recall the change of variables for the Helmholtz equation,which follows from[27,Lemma 2]. Lemma 2.1Let D1⊂⊂ D2⊂⊂ D3be smooth bounded open subsets of Rd,T be a diffeomorphism fromontosuch that T(x)=x onand σ∈L∞(D2D1).Let u∈H1(D2D1)and set v=u◦T−1.Then for someif and only if Moreover, Here and in what follows,we use the standard notations: where x=T−1(y)and J(x)=|det DT(x)|. We are ready to give[27,Definition 1]. Definition 2.1(Reflecting Complementary Media)LetΩ1⊂⊂ Ω2⊂⊂ Ω3be smooth connected bounded open subsets of Rd.The media(A,Σ)in Ω3Ω2and(−A,−Σ)in Ω2Ω1are said to be reflecting complementary,if there exists a diffeomorphismsuch that and the following two conditions hold: (1)There exists a diffeomorphism extension of F,which is still denoted by F,fromΩ2for some x1∈Ω1. (2)There exists a diffeomorphismsuch that3In(2.16)–(2.17),F and G denote some diffeomorphism extensions of F and G in a neighborhood of ∂Ω2 and of∂Ω3,respectively. and Some comments on the definition are useful.If k=0,then the condition onΣis irrelevant in Definition 2.1.Condition(2.15)implies that(A,Σ)in Ω3Ω2and(−A,−Σ)in Ω2Ω1are complementary in the “usual sense”4In fact,complementary media had not been defined precisely,the property mentioned here appeared in various known examples..The term “reflecting” in the definition comes from(2.16)and the assumption Ω1⊂ Ω2⊂ Ω3.Conditions(2.15)–(2.16)imply that u0(the solution toδ=0 if it exists)and u1,0:=u0◦F satisfy the same equation inΩ3Ω2and the same Cauchy data on ∂Ω2by Lemma 2.1,hence the reflecting technique in Section 2.1 can be used.Conditions(2.15)–(2.16)are the key assumptions.Conditions(1)–(2)are mild ones.Introducing G makes the analysis more accessible(see also Sections 3–5).In general,it is not easy to verify the condition(2.15).However,given(A,Σ)in Ω3Ω2,it is easy to obtain(−A,−Σ)inΩ2Ω1,such that(2.15)holds by choosing an arbitrary diffeomorphismand defining(A,Σ)inΩ2Ω1by(F−1∗A,F−1∗Σ).This process was repeatedly used in various applications of NIMs(see Sections 3–5). Remark 2.2The definition given here simplifies lightly the one introduced in[27],and suffices for various applications of NIMs discussed later. Here and in what follows in this section,we confine ourselves to the quasi-static regime:k=0.The finite frequency regime(k>0)can be proceeded similarly(see[27]).The following result follows from[27,Theorems 1–2]. Theorem 2.1Let d=2,3,δ>0,f ∈ L2(Ω)and letthe unique solution to(2.11), Assume that A inΩ3Ω2and−A inΩ2Ω1are reflecting complementary and suppfor someΩ2⊂⊂Ω3⊂⊂Ω.We have the following. (a)Case 1:f is compatible(see Definition 2.2).Then(uδ)converges weakly in H1(Ω)and strongly in L2(Ω)to u0∈ H10(Ω)the unique solution to asδ→0.Moreover,whereis the unique solution to (b)Case 2:f is not compatible.We have In the statement of Theorem 2.1,we use the following definition[27,Definition 2]. Definition 2.2(Compatibility Condition)Assume that A inΩ3Ω2and−A inΩ2Ω1are reflecting complementary.Then f∈L2(Ω)with supp f∩Ω3=Ø is said to be compatible if and only if whereis defined in(2.20). Here and in what follows,for a smooth bounded open subset D ⊂ Rd,on∂D,νdenotes the outward unit normal vector. The proof of Theorem 2.1 is quite straightforward from the definition of reflecting complementary media and the heuristic argument presented in Subsection 2.1.We first assume that u0exists.As in Subsection 2.1,definein RdΩ3andinΩ3.Set Then u1,0=u0inΩ3Ω2andsatisfiesby Lemma 2.1.It follows that V=u0inTherefore,the compatibility condition holds,and u0is uniquely given by Assume that the compatibility condition holds.Define u0by(2.23).One can verify thatis a solution to(2.19)(see[27,Subsection 3.2.2]for the details).To prove that uδ→ u0weakly asδ→ 0 in this case,we proceed as follows.Define vδ=uδ−u0in Ω.Then Multiplying the equation by,the conjugate of vδ,considering the real part and the imaginary part,we have(see[27,Lemma 1]) for some positive constant C independent ofδ.Hence(uδ)is bounded in H1(Ω).Since u0is unique,a standard compactness argument yields that uδ→ u0weakly in H1(Ω)and strongly in L2(Ω). It remains to prove Case 2.The proof is based on a contradiction argument.Assume that(2.21)does not hold.It follows that uδn→ u0weakly in H1(Ω)for some(δn) → 0+.Then V=u0inΩ3Ω2and f is compatible.We have a contradiction. The compatibility condition is not easy to verify in general.Nevertheless,we have[27,Corollary 2]. Proposition 2.1Let d=2,3,δ>0,f∈ L2(Ω).Assume that A inΩ3Ω2and−A inΩ2Ω1are reflecting complementary for someΩ2⊂⊂ Ω3⊂⊂ Ω,and G∗F∗A=A in Ω3Ω2.Then f∈L2(Ω)with supp f∩Ω3=Ø is compatible. Proposition 2.1 is a consequence of the factsinceIts applications on superlensing and cloaking a source via ALR are given in Sections 3 and 5 respectively.It is clear that the setting of Nicorovici,McPhedran and Milton satisfies Proposition 2.1 withΩj=Bj(j=1,2,3),and F and G are the Kelvin transforms used in the heuristic argument in Subsection 2.1. The construction of a superlens using NIMs was first suggested by Veselago [49]for a slab lens.The superlensing property of the slab lens was also studied by Veselago via the ray theory in[49].Later,the study of cylindrical lenses in the two dimensional quasistatic regime,the Veselago slab,cylindrical lenses and spherical lenses in the finite frequency regime were considered by Nicorovici,McPhedran and Milton in[42],Pendry in[44–45],and Pendry and Ramakrishna in[47],respectively for some constant isotropic objects. Figure 1 The lensing device contains two parts.The first part(the red region)in B r 2B r 1 is the complement of I in B r 3B r 2.The second part(the green region)is m d−2I in B r 1B r 0.The magnified region is B r 0. Our lens contains two parts.The first one is given by and the second one is Here r1and r2are such that With the loss,the medium is characterized by sδA,5In[28],sδ= −1+iδin B r 2B r 1;nevertheless this point is not essential.where LetΩ be a smooth open subset of Rd(d=2,3)such that Br3⊂ Ω.Given f∈ L2(Ω),let uδ,be respectively the unique solution to and We have the following theorem. Theorem 3.1Let d=2,3,f∈L2(Ω)with supp f⊂ΩBr3.We have For an observer outside Br3,the object a in Br0would act like by(3.8).Then one has a superlens whose magnification is m. We next give some comments on the lens construction and explain how to obtain Theorem 3.1 from Theorem 2.1 and Proposition 2.1.The first part of the lens withα=2 is the same as the known superlens constructions mentioned.Given r1,one requires thatsince a superlens of m times magnification is considered as in[42,45,47]and the comments for(2.3)(see also(3.7)and Theorem 3.1).Letbe defined bywhereThensatisfies This implies,since A=md−2I in Br1Br0and r2=mr0, This is the place where the second part of the construction plays its role.From(3.9)–(3.10),one has Theorem 3.1 is now a direct consequence of Theorem 2.1 and Proposition 2.1. A more delicate analysis implies that(3.8)holds for every f∈ L2(Ω)with supp(see Theorems 5.1 and 5.3).Theorem 3.1 can be easily extended for the finite frequency regime using the concept of reflecting complementary media since Theorem 2.1 and Proposition 2.1 also hold in this regime(see[28]for the original proof). This section ends with the following question on the necessity of the second layer in the lens construction. Op en Question 3.1Does Theorem 3.1 hold where A is given in(3.5)with r1=r0? Cloaking using complementary media was suggested by Lai et al.in[21].The idea is to cancel the effect of the object by its complementary medium.The study of this problem faces two difficulties.Firstly,this problem is unstable since the equations describing the phenomenon have sign changing coefficients,hence the ellipticity and the compactness are lost in general.Secondly,the localized resonance might appear. Let us describe how to cloak the region B2r2Br2for some r2>0 in the quasistatic regime in which the medium is characterized by a matrix a using complementary media.The assumption on the cloaked region by all means imposes no restriction,since any bounded set is a subset of such a region provided that the radius and the origin are appropriately chosen.The idea suggested by Lai et al.in[21](in two dimensions)is to construct a complementary medium in Br2Br1for some 0 We will assume that The complementary medium in Br2Br1is given by whereis the Kelvin transform with respect to∂Br2.Concerning the second part,the medium in Br1is given by The reason for this choice is the condition where G is the Kelvin transform with respect to∂Br3since the homogeneous medium is filled(see Theorem 2.1 and(2.20)).The cloaking scheme is illustrated in Figure 2. Figure 2 The cloaking device contains two parts.The first part(the red and orange regions)in is the complement of b which consists of a(grey and blue grey regions)in and I in.The second part(the blue region) is to fill the space which disappears by the cancelation. In two dimensions,the medium in Br1is I,as used in[21],while it is not I in three dimensions.With the loss,the medium is characterized by sδA where Givenbe respectively the unique solution to and We established[31,Theorem 1].6In[31],sδ= −1+iδin B r 2B r 1;nevertheless this point is not essential. Theorem 4.1Let d=2,3,f∈ L2(Ω)with supp f⊂ ΩBr3.There existsℓ>0,depending only on r2,and the ellipticity and the Lipschitz constants of b such that if r3>ℓr2then For an observer outside Br3,the medium in Br3looks as the homogeneous one by(4.7).Then one has cloaking. ProofWe only consider the two dimensional case;the proof in three dimensions follows similarly.Multiplying(3.6)by,integrating in Ω,considering first the imaginary part and then the real part,we have Here and in what follows in the proof,C denotes a positive constant independent ofδand f.As in Section 2,defineandas follows: Applying Lemma 2.1,we have FixApplying[31,Lemma 1.1](a three spheres inequality),we have,forℓlarge enough, where This implies Applying Lemma 2.1 again,we obtain From(4.12),one can represent u1,δ,and u2,δof the forms forSince,by(4.8), we obtain From(4.13)–(4.15),a straightforward computation gives A combination of(4.14)–(4.15)and(4.17)yields,in Br3B3r2, Set where It is clear from the definition of We claim that Here and in what follows[·]denotes the jump of a quantity across the boundary.Admitting this,we derive from(4.21)that asδis small.Without loss of generality,one may assume thatweakly in H1(Ω(∂Br3∪∂Br1)).It is clear thatandinΩ and hence u=b u.Since the limit is unique,the convergence holds for the whole family.The conclusion follows in two dimensions. It remains to prove(4.22).In fact,it is a consequence of(4.8),(4.11),(4.16),and the definition of.The proof is complete. Remark 4.1In the proof,we removethe singular part of,fromin Br3Br2.The functionbecomes more and more singular as r is smaller and smaller and behaves smoothly for large r.This is the idea of the removing localized singularity technique which was introduced in[28,31].The removing termis in the same spirit with the removing term of“infinite” energy in the theory of Ginzburg-Landau equations proposed by Bethuel,Brezis,and Hélein in[4]and was inspired by their work.In[4],after removing the infinite energy term,one obtained the renormalized energy introduced there.Here,after removing the bad term,the gluing functionsatisfies a standard elliptic equation which characterizes the reflecting medium. Remark 4.2Theorem 4.1 hods if A in Br2is chosen such that F∗A=b in Br3Br2and G∗F∗A=I in Br3for some F and G as in Definition 2.1 with Ωj=Brjfor j=1,2,3.This means for such a pair(F,G).In particular,Theorem 4.1 hods if A in Br2is given in(4.4)in whichfor someα>1(see also Section 3). Remark 4.3The method presented here was extended for the Helmholtz equation in[38]in joint work with Nguyen.To this end,we established new type of three spheres inequalities for the Helmholtz equations in which no condition of the smallness of radii is imposed. We have the following question on the necessity of the layer I in Br3B2r2. Op en Question 4.1Does Theorem 4.1 hold where A is given in(3.5)with r3=2r2? Remark 4.4Cloaking can also be achieved via transformation optics or changes of variables.Resonance might also appear in this context(see[19,25–26,39]).It is shown in[26]that in the resonance case cloaking might not be achieved and the field inside the cloaked region can depend on the field outside.Cloaking can also be achieved in the time regime via change of variables(see[40–41]). (1)The localized resonance,i.e.,the fields blow up in some regions and remain bounded in some others as the loss goes to 0. (2)The connection between the localized resonance and the blow up of the power as the loss goes to 0. Their work has attracted many investigations,see[2–3,11–14,18,24,37]in which special structures were considered due to the use of the separation of variables or the blow up of the power was investigated.An important class of NIMs in which the localized resonance might appear is the class of reflecting complementary media in Section 2(see also Sections 3–4).Nevertheless,the complementary property is not enough to ensure that cloaking a source via ALR takes place,and there is no connection between the blow up of the power and the localized resonance in general as discussed in[37](joint work with Nguyen). In[29–30],we investigated CALR for a source for a subclass of complementary media called the class of doubly complementary media for a core-shell structure.Let d=2,3,andΩbe a smooth open bounded subset of Rd,and let 0 Let A be a symmetric uniformly elliptic matrix-valued function defined inΩ.The definition of doubly complementary media[30,Definition 1.2]is as follows. Definition 5.1The medium s0A is said to be doubly complementary if for some r3>0 with Br3⊂⊂Ω,A in Br3Br2and−A in Br2Br1are reflecting complementary,and for some F and G coming from Definition 2.1 withΩj=Brjfor j=1,2,3. Remark 5.1Roughly speaking,the shell Br2Br1is not only reflecting complementary to a part of the matrix but also to a part of the core.Indeed,−A in Br2Br1is not only complementary to A in Br3Br2but also to A in(a subset of Br1)(see Figure 3). Figure 3 s0A is doubly complementary:−A in B r 2B r 1(the red region)is complementary to A=F∗A in B r 3B r 2(the grey region)and A=K∗A with K=F−1◦G−1◦F in K(B r 2B r 1)(the blue grey region). Let f∈ L2(Ω)with supp f∩Br2=Ø and letbe the unique solution to The power Eδ(uδ)is defined by(see,e.g.,[23]) Using the fact that uδ=0 on ∂Ω,one has8One way to obtain this inequality is to multiply(5.3)by integrate on Ω,and consider the real part. for some positive constants C independent of f and δ∈ (0,1).Letbe the unique solution to Here fδ=cδf and cδis the normalization constant such that In what follows in this section,we assume that The equivalence between the blow up of the power and cloaking a sourcevia ALR for doubly complementary media can be derived from the following result[30,Proposition 4.1]. Theorem 5.1Let d=2,3,letwith supp gn⊂ ΩBr2,and letbe the unique solution to Assume that s0A is doubly complementary,gn→ g weakly in L2(Ω)for some g∈ L2(Ω),and Thenweakly inwhereis the unique solution to Here,as usual, The equivalence between the blow up of the power and the cloaking a source via ALR can be obtained from Theorem 5.1 as follows.Suppose that the power blows up,i.e., Then,by Theorem 5.1,vδn→ 0 in Ω Br3.The source αδnf is not seen by observers far away from the shell:The source is cloaked.Note that the localized resonance happens in this case since(5.6)takes place.If the power of uδnremains bounded,thenweakly in H1(ΩBr3),whereis the unique solution tothe source is not cloaked. We next present the proof in the case A=I in Br3Br2in two dimensions to highlight the use of the removing localized singularity technique.This situation is already non-trivial and the standard separation of variables is out of reach,since A can be arbitrary outside Br3. Sketch of the Proof of Theorem 5.1(Under the additional assumption that A=I in Br3Br2and d=2.)Using(5.4),we derive from(5.8)that Define Since A=I in Br3Br2,it follows from(5.2)and Lemma 2.1 that and From(5.10),v1,nand v2,ncan be represented respectively as follows: forUsing(5.11),as in the proof of Theorem 4.1,there existssuch thatand where N(·,r)is defined in(4.10).The conclusion now follows as in the proof of Theorem 4.1.Define Thenweakly inThe proof is complete. To develop the approach presented above for a general core-shell structure,in[30],we introduced and implemented the separation of variables technique to solve Cauchy problems in a general shell.The main idea behind the method is to find an appropriate dense set of solutions to the equation to replace rℓe±iℓθand r−ℓe±iℓθin the case A=I and d=2.Indeed,from[30,Proposition 4.2],there exist two families(vℓ)ℓ≥1and(wℓ)ℓ≥1such that and Here v0=1 in Br3Br2and w0∈H1(Br3Br2)is the unique solution to More properties on the behaviors of(wℓ)and(vℓ)are required in the proof of Theorem 5.1(see[30,Proposition 4.2]for the details).Properties(5.13)–(5.14)are very suitable for the use of removing localized singularity technique.Due to the lack of the orthogonality of vℓand wℓ,the implementation of this technique in the general case is more delicate. In[30],we also showed that the power blows up if the source is located “near”the shell even for reflecting complementary media(see[30,Theorem 2]). Theorem 5.2Let d=2,3,f ∈ L2(Ω)with supp f ⊂ ΩBr2,and letbe the unique solution to Assume that A in Bbr3Br2and−A in Br2Bbr1are reflecting complementary for some r1≤withThere exists a constantindependent ofδand f such that if there is no w ∈ H1(Br∗Br2)with the properties then Assume in addition that A=I in Bbr3Br2,then ProofWe will sketch the proof in the caseand A=I in Br3Br2.The proof in the general case follows by the same approach via three spheres inequalities.The proof is again based on the use of reflection.Defineand set.We have We prove by contradiction that where δn=2−n.Assume that We claim that(wδn)is a Cauchy sequence in H1(Br∗Br2).Indeed,set It follows from(5.19)that where if∆φ=0 in BR2and 0 This contradicts the non-existence of w.Hence(5.18)holds.The proof is complete. Remark 5.2Theorem 5.2 implies the result in[18]on the blow up of the power. Concerning the boundedness of the power,we can establish the following more general result. Theorem 5.3Let d=2,3,f ∈ L2(Ω),and letbe the unique solution to(5.3).Assume that s0A is doubly complementary and supp f∩Br3=Ø.Then Assume in addition that A=I in Br3Br2.If there existsfor somewith the properties for some 0<α<1,then Remark 5.3The first part(5.20)is from Theorem 2.1.The second part(5.21)withis given in[30,Theorem 3].The proof in this case is based on a kind of removing singularity technique.The proof of the result stated here follows similarly.One just needs to replace the constantξℓdefined in[30,(3.10)]byThe details are left to the reader. Using Theorems 5.1 and 5.2,we can construct a cloaking device to cloak a general source concentrate on a manifold of codimension 1 in an arbitrary medium(see[30,Section 5]for the details). Let k>0 and let A be a(real)uniformly elliptic symmetric matrix defined on Rd(d≥2),andΣbe a bounded real function defined on Rd.Assume that9The smoothness assumption of A is mainly required for the use of the unique continuation principle.It can be omitted in two dimensions. for some R0>0.Let D⊂⊂BR0be a bounded open subset in Rdof class C2.Set,forδ≥0, In[32],we studied the well-posedness of the following equation: under various conditions on A andΣ.To make sure that physics solutions are considered,we also study the limiting absorption principle associated with(6.1),i.e.,the convergence of uδto u0(in an appropriate sense).Here uδ∈ H1(Rd)is the unique solution of the equation Recall that a solutionof the equation for some R>0,is said to satisfy the outgoing condition if Denote and,forτ>0,set The well-posedness of the Helmholtz equation with sign changing coefficients was first established by Costabel and Stephan in[15].They proved,by the integral method,that(6.1)is well-posed if A=I in RdD and A= λI in D provided thatλis positive constant not equal to 1.Later,Ola in[43]proved,using the integral method and the pseudo-differential operators theory,that(6.1)is well-posed in three and higher dimensions if the interface Γ is strictly convex and connected even thoughλ=1,i.e.,A=I in Rd.His result was extended for the case whereΓhas two connected components by Kettunen,Lassas and Ola in[17].Recently,the well-posedness was extensively studied by Bonnet-Ben Dhia,Ciarlet,and their coauthors in[5–9]by the T-coercivity approach.This approach was introduced by Bonnet-Ben Dhia,Ciarlet,and Zwölf in[9]and is related to the(Banach-Necas-Babuska)inf-sup condition.The sharpest condition for the acoustic setting in this direction,obtained by Bonnet-Ben Dhia,Chesnel,and Ciarlet in[5],is that(6.1)is well-posed in the Fredholm sense(this means that compactness holds),if A is isotropic,i.e.,A=aI for some positive function a,and the contrast of a is not 1 on each connected component ofΓ. The starting point in[32]is to use reflections to obtain Cauchy’s problems from the Helmholtz equations with sign changing coefficients as previously discussed in various contexts.The use of reflections to study NIMs was also considered by Milton et al.in[24]and by Bonnet-Ben Dhia,Ciarlet,and their coauthors in their T-coercivity approach(see,e.g.,[5]and references there in).However,there is a difference between the use of reflections in[24]and[5]and in our work.In[24],the authors used reflections as a change of variables to obtain a new simplesetting from an old more complicated one,and hence the analysis of the old problem becomes simpler.In[5],the authors used a standard reflection to build test functions for the inf-sup condition to obtain an a prioriestimate for the solution.Our use of reflections is to derive Cauchy problems.This can be done in a very flexible way via a change of variables formula stated in Lemma 2.1 as observed in[27].The limiting absorption principle and the well-posedness of(6.1)are then based on a priori estimates for these Cauchy problems. In[32],we introduced three approaches to obtain a priori estimates for the Cauchy problems.The first one follows from a priori estimates for elliptic systems imposing implementing boundary conditions.This is based on the classic work of Agmon,Douglis,and Nirenberg in[1].Applying their result,we proved[32,Theorem 1]. Theorem 6.1Let f∈L2(Rd)with supp f⊂⊂BR0and let uδ∈H1(Rd)(0<δ<1)be the unique solution to(6.2).Assume thatfor someτ>0,and A+(x),A−(x)satisfy the(Cauchy)complementing condition with respect to directionν(x)for all x∈Γ.Then Moreover,uδ→ u0weakly inand strongly inasδ→0,whereis the unique outgoing solution to(6.1).Consequently, Here CRdenotes a positive constant independent of f andδ. We recall the following definition. Definition 6.1(see[1])Two constant positive symmetric matrices A1and A2are said to satisfy the(Cauchy)complementing condition with respect to direction e∈ ∂B1if and only if for allthe only solution(u1(x),u2(x))to the formwith x=y+te whereand t= ⟨x,e⟩,of the following system: which is bounded inis(0,0). Here and in what follows,for a unit vector e,the following notations are used: denotes the Euclidean scalar product in Rd. An algebraic characterization of the complementing condition is[32,Proposition 1]. Proposition 6.1Two constant positive symmetric matrices A1and A2are said to satisfy the complementing condition with respect to direction e∈ ∂B1if and only if where In particular,if A2>A1then A1and A2satisfy the complementing boundary condition for all e∈ ∂B1. As a consequence of Theorem 6.1 and Proposition 6.1,we obtained[32,Corollary 1]. Corollary 6.1Let f∈L2(Rd)with supp f⊂⊂BR0,and let uδ∈H1(Rd)(0<δ<1)be the unique solution of(6.2).Assume thatfor someτ>0,and A+(x)>A−(x)or A−(x)>A+(x)for all x∈Γ.Then the conclusion of Theorem 6.1 holds. To our knowledge,Corollary 6.1 is new and cannot be obtained by the known approaches mentioned above.It is in the same spirit of the one of Bonnet-Ben Dhia,Chesnel,and Ciarlet in[5];nevertheless,A+and A−are not assumed to be isotropic here. We next discuss briefly the proof of Theorem 6.1.We recall the result as follows. Lemma 6.1(see[1])Let D be a smooth bounded open subset of Rd,and A1and A2be two symmetric uniformly elliptic matrices defined in D of classLet f1,f2∈L2(D),and let u1,u2∈H1(D)be such that Assume that A1and A2satisfy the(Cauchy)complementing condition with respect to direction ν(x)for all x∈ Γ.We have We confine ourselves to the caseδ=0 and give the ideas of the proof of(6.5).Note that the uniqueness of u0can be obtained as in the standard setting where the coefficients are positive by Rellich’s lemma.Defineas follows: Let v0be the reflection of u0throughΓ by F,i.e.,v0=u0◦F−1in Dτ.By Lemma 2.1, and Note that A+and A−satisfy the complementing condition on Γ if and only if F∗A−and A+satisfy the complementing condition onΓby Proposition 6.1.Applying Lemma 6.1 and using the outgoing condition,one obtains The conclusion now follows from the uniqueness via a standard compactness argument(see[32,Section 2]for the details). One can verify that if F∗A+=A−on Γ,then the complementing condition is not satisfied(see Proposition 6.1).To deal with this situation,in[32],we developed a second approach to obtain a priori estimates for the Cauchy problems.This is a variational approach and based on the Dirichlet principle.Using this approach,we established the following theorem(see[32,Theorem 2]). Theorem 6.2Let f∈L2(Rd)with supp f⊂BR0,and let uδ∈H1(Rd)(0<δ<1)be the unique solution to(6.2).Assume that there exists a reflection F from UD onto Dτfor some τ>0 and for some smooth open set U ⊃⊃D,i.e.,F is diffeomorphism and F(x)=x onΓ,such that on each connected component of Dτ,for some c>0 and 0< α <2.Setin Dτ.Then Moreover,uδ→ u0weakly inand strongly inasδ→ 0,where u0∈is the unique outgoing solution to the equation(6.1)such that the LHS of (6.12)is finite where v0=u0◦F−1in Dτ.Consequently, Here CRdenotes a positive constant independent of f andδ. The unique solution,which is obtained by the limiting absorption principle,might not be inin this case.The definition[32,Definition 2]is as follows. Definition 6.2Let f∈L2(Rd)with compact support,and let F be a reflection from UD to Dτfor someτ>0(small)and for some open set D ⊂⊂ U,i.e.,F is diff eomorphism and F(x)=x onΓ.A functionsuch that the LHS of(6.12)is finite is said to be a solution to(6.1)if and Remark 6.1? Since the LHS of(6.12)is finite,it follows that u0−v0∈H12(Γ)andHence requirement(6.14)makes sense.It is clear that the definition of weak solutions in Definition 6.2 coincides with the standard definition of weak solutions when α =0 by Lemma 2.1.Requirements in(6.14)–(6.15)can be seen as generalized transmission conditions. Once the uniqueness is obtained,the stability is based on a compactness argument.The requirement α<2 is required in the compactness argument(see[32,Lemma 7]);wedo not know if this condition is necessary.As a consequence of Theorem 6.2,one can prove[32,Corollary 2]. Corollary 6.2Let f∈L2(Rd)with supp f⊂BR0,and let uδ∈H1(Rd)(0<δ<1)be the unique solution to(6.2).Assume that A◦F−1(x)or A(x)is isotropic for x∈ Dτ,and in each connected component Dτfor some smallτ>0 and for some c>0,where F is given by(6.9).Then Moreover,uδ→ u0weakly inasδ→0,whereis the unique outgoing solution to(6.1)and Remark 6.2Applying Corollary 6.2 for the isotropic case,one rediscovers and extends the result obtained by Bonnet Ben-Dhia,Chesnel and Ciarlet in[5]. We next present another consequence of Theorem 6.2 for the caseα=1.The following notation is used. Definition 6.3The boundary Γ of D is called strictly convex,if all its connected components are the boundary of strictly convex sets. We are ready to present[32,Corollary 2]. Corollary 6.3Let d≥3 and D be of class C3.Let f∈L2(Rd)with supp f⊂BR0and let uδ∈H1(Rd)(0< δ<1)be the unique solution of(6.2).Assume that A is constant in each connected component of a neighborhood ofΓandΓis strictly convex.There exist c>0,τ>0,a smooth open subset U ⊃⊃ D,a reflection F:U → Dτsuch that F∗A−A ≥ c dist(x,Γ)I or A − F∗A ≥ c dist(x,Γ)I on each connected component of Dτ.Then(6.11)holds.Moreover,uδ→ u0weakly inasδ→0,wheresatisfies(6.12),and u0is the unique outgoing solution to(6.1). Remark 6.3The reflection F in Corollary 6.3 is not given by(6.9).Its choice is quite subtle and depends on the fundamental form ofΓ(see[32,Proof of Corollary 2]).Corollary 6.3 does not hold in two dimensions.The strict convexity ofΓis necessary in three dimensions.In four or higher dimensions,the strict convexity ofΓcan be relaxed(see[32,Remark 10]). We next return to the proof of Theorem 6.2.An important step in the proof is to obtain estimate for the Cauchy problem.A result of this type is the following lemma which is somehow a replacement of Lemma 6.1 in this context and a special case of[32,Lemma 5].The proof is based on the Dirichlet principle. Lemma 6.2Let D be a smooth bounded open subset of Rd,and A1and A2be two symmetric uniformly elliptic matrices defined in D.Let f1,f2∈L2(D),and let u1,u2∈H1(D)be such that Assume that Then ProofBy considering the real part and the imaginary part separately,without loss of generality,one may assume that all functions in Lemma 6.2 are real.Set Multiplying the equation of ujby uj(for j=1,2)and integrating on D,we have Using(6.17)–(6.18),we derive from(6.21)that Here and in what follows,C denotes a positive constant independent of fj,h,ujfor j=1,2.By the Dirichlet principle,we have A combination of(6.17)–(6.18)and(6.23)yields Adding(6.22)and(6.24),we obtain the conclusion. Similar conclusion holds in the case F∗A=A in Dτunder additional assumptions onin Dτfor some β >0(see[32,Theorem 3]for a more general result).The unique solution in this case is not even inAs far as we know,[32,Theorem 3]is the first result on the limiting absorption principle and the well-posedness of the Helmholtz equations with sign changing coefficients where the conditions on the coefficients contains the zero order termΣ. Remark 6.4The results mentioned here showed that the complementary property of media is necessary for the occurrence of the resonance.In[32,Proposition 2],we showed that even in the case(F∗A,F∗Σ)=(A,Σ)in B ∩ Dτfor some open set B with B ∩ ΓØ,the system is resonant in the following sense:There exists f with supp f⊂⊂ BR0Γ,such thatfor some K ⊂⊂ BR0Γ.This implies the optimality of the results mentioned above.The proof of[32,Proposition 2]is inspired from the one of Theorem 5.2. Notes addedVery recent progress on negative index materials can be found in[34–36].The answers to Open Questions 3.1 and 4.1 are negative(see[34]). AcknowledgementsThe author thanks Professor Haïm Brezis deeply for his encouragement,his guidance,and his support from his Ph.D studies.His joint work with Bethuel and Hélein on the Ginzburg-Landau equation in[4]inspired the author to introduce the removing localized singularity technique to handle the localized resonance which appears naturally in the study of negative index materials.The author also thanks Professor Graeme Milton for useful discussions on the subject. [1]Agmon,S.,Douglis,A.and Nirenberg,L.,Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions.II,Comm.Pure Appl.Math.,17,1964,35–92. [2]Ammari,H.,Ciraolo,G.,Kang,H.,et.al.,Anomalous localized resonance using a folded geometry in three dimensions,Proc.R.Soc.Lond.Ser.A,469,2013,20130048. [3]Ammari,H.,Ciraolo,G.,Kang,H.,et.al.,Spectral theory of a Neumann-Poincaré-type operator and analysis of cloaking due to anomalous localized resonance,Arch.Rational Mech.Anal.,218,2013,667–692. [4]Bethuel,F.,Brezis,H.and Helein,F.,Ginzburg Landau vortices,Progress in Nonlinear Differential Equations and Their Applications.,13,Birkhäuser,Boston,1994. [5]Bonnet-Ben Dhia,A.S.,Chesnel,L.and Ciarlet,P.,T-coercivity for scalar interface problems between dielectrics and metamaterials,ESAIM Math.Model.Numer.Anal.,46,2012,1363–1387. [6]Bonnet-Ben Dhia,A.S.,Chesnel,L.and Ciarlet,P.,T-coercivity for the Maxwell problem with signchanging coefficients,Comm.Partial Differential Equations,39,2014,1007–1031. [7]Bonnet-Ben Dhia,A.S.,Ciarlet,P.and Zwölf,C.M.,Two-and three-field formulations for wave transmission between media with opposite sign dielectric constants,J.Comput.Appl.Math.,204,2007,408–417. [8]Bonnet-Ben Dhia,A.S.,Ciarlet,P.and Zwölf,C.M.,A new compactness result for electromagnetic waves.Application to the transmission problem between dielectrics and metamaterials,Math.Models Methods Appl.Sci.,18,2008,1605–1631. [9]Bonnet-Ben Dhia,A.S.,Ciarlet,P.and Zwölf,C.M.,Time harmonic wave diffraction problems in materials with sign-shifting coefficients,J.Comput.Appl.Math.,234,2010,1912–1919. [10]Bouchitté,G.and Felbacq,D.,Homogenization near resonances and artificial magnetism from dielectrics,C.R.Math.Acad.Sci.Paris,339,2004,377–382. [11]Bouchitté,G.and Schweizer,B.,Cloaking of small objects by anomalous localized resonance,Quart.J.Mech.Appl.Math.,63,2010,437–463. [12]Bouchitté,G.and Schweizer,B.,Homogenization of Maxwell’s equations in a split ring geometry,Multiscale Model.Simul.,8,2010,717–750. [13]Brezis,H.,Functional Analysis,Sobolev Spaces and Partial Differential Equations,Universititex,Springer-Verlag,New York,2010. [14]Bruno,O.P.and Lintner,S.,Superlens-cloaking of small dielectric bodies in the quasistatic regime,J.Appl.Phys.,102,2007,12452. [15]Costabel,M.and Stephan,E.,A direct boundary integral equation method for transmission problems,J.Math.Anal.Appl.,106,1985,367–413. [16]Guenneau,S.and Zolla,F.,Homogenization of 3d finite chiral photonic crystals,Physica B:Condens.Matter,394,2007,145–147. [17]Kettunen,H.,Lassas,M.and Ola,P.,On absence and existence of the anomalous localized resonance without the quasi-static approximation.http://arxiv.org/abs/1406.6224 [18]Kohn,R.V.,Lu,J.,Schweizer,B.and Weinstein,M.I.,A variational perspective on cloaking by anomalous localized resonance,Comm.Math.Phys.,328,2014,1–27. [19]Kohn,R.V.,Onofrei,D.,Vogelius,M.S.and Weinstein,M.I.,Cloaking via change of variables for the Helmholtz equation,Comm.Pure Appl.Math.,63,2010,973–1016. [20]Kohn,R.V.and Shipman,S.P.,Magnetism and homogenization of microresonators,Multiscale Model.Simul.,7,2008,62–92. [21]Lai,Y.,Chen,H.,Zhang,Z.and Chan,C.T.,Complementary media invisibility cloak that cloaks objects at a distance outside the cloaking shell,Phys.Rev.Lett.,102,2009,093901. [22]Milton,G.W.,Nicorovici,N.A.,McPhedran,R.C.and Podolskiy,V.A.,A proof of superlensing in the quasistatic regime,and limitations of superlenses in this regime due to anomalous localized resonance,Proc.R.Soc.Lond.Ser.A,461,2005,3999–4034. [23]Milton,G.W.and Nicorovici,N.A.P.,On the cloaking effects associated with anomalous localized resonance,Proc.R.Soc.Lond.Ser.A,462,2006,3027–3059. [24]Milton,G.W.,Nicorovici,N.P.,McPhedran,R.C.,et.al.,Solutions in folded geometries,and associated cloaking due to anomalous resonance,New J.Phys.,10,2008,115021. [25]Nguyen,H.-M.,Cloaking via change of variables for the Helmholtz Equation in the whole space,Comm.Pure Appl.Math.,63,2010,1505–1524. [26]Nguyen,H.-M.,Approximate cloaking for the Helmholtz equation via transformation optics and consequences for perfect cloaking,Comm.Pure Appl.Math.,65,2012,155–186. [27]Nguyen,H.-M.,Asymptotic behavior of solutions to the Helmholtz equations with sign changing coefficients,Trans.Amer.Math.Soc.,367,2015,6581–6595. [28]Nguyen,H.-M.,Superlensing using complementary media,Ann.Inst.H.Poincaré Anal.Non Linéaire,32,2015,471–484. [29]Nguyen,H.-M.,Cloaking via anomalous localized resonance,a connection between the localized resonance and the blow up of the power for doubly complementary media,C.R.Math.Acad.Sci.Paris,353,2015,41–46. [30]Nguyen,H.-M.,Cloaking via anomalous localized resonance for doubly complementary media in the quasistatic regime,J.Eur.Math.Soc.,17,2015,1327–1365. [31]Nguyen,H.-M.,Cloaking using complementary media in the quasistatic regime,Ann.Inst.H.Poincaré Anal.Non Linéaire,33,2016,1509–1518. [32]Nguyen,H.-M.,Limiting absorption principle and well-posedness for the Helmholtz equation with sign changing coefficients,J.Math.Pures Appl.,106,2016,342–374. [33]Nguyen,H.-M.,Reflecting complementary and superlensing using complementary media for electromagnetic waves,submitted. [34]Nguyen,H.-M.,Cloaking an arbitrary object via anomalous localized resonance:the cloak is independent of the object,submitted.https://arxiv.org/abs/1607.06492 [35]Nguyen,H.-M.,Cloaking via anomalous localized resonance for doubly complementary media in the finite frequency regime,submitted.https://arxiv.org/abs/1511.08053 [36]Nguyen,H.-M.,Cloaking using complementary for electromagnetic waves,submitted.https://arxiv.org/abs/1701.02339 [37]Nguyen,H.-M.and Nguyen,H.L.,Complete resonance and localized resonance in plasmonic structures,ESAIM:Math.Model.Numer.Anal.,49,2015,741–754. [38]Nguyen,H.-M.and Nguyen,H.L.,Cloaking using complementary media for the Helmholtz equation and a three spheres inequality for second order elliptic equations,Trans.Amer.Math.Soc.,Ser.B,2,2015,93–112. [39]Nguyen,H.-M.and Vogelius,M.S.,Full range scattering estimates and their application to cloaking,Arch.Rational Mech.Anal.,203,2012,769–807. [40]Nguyen,H.-M.and Vogelius,M.S.,Approximate cloaking for the wave equation via change of variables,SIAM J.Math.Anal.,44,2012,1894–1924. [41]Nguyen,H.-M.and Vogelius,M.S.,Approximate cloaking for the full wave equation:A study of the Lorentz model,J.Math.Pures Appl.,106,2016,797–836. [42]Nicorovici,N.A.,McPhedran,R.C.and Milton,G.M.,Optical and dielectric properties of partially resonant composites,Phys.Rev.B,49,1994,8479–8482. [43]Ola,P.,Remarks on a transmission problem,J.Math.Anal.Appl.,196,1995,639–658. [44]Pendry,J.B.,Negative refraction makes a perfect lens,Phys.Rev.Lett.,85,2000,3966–3969. [45]Pendry,J.B.,Perfect cylindrical lenses,Optics Express,1,2003,755–760. [46]Pendry,J.B.,Holden,A.J.,Robbins,D.J.and Stewart,W.J.,Magnetism from conductors and enhanced nonlinear phenomena,IEEE Trans.Microw.Theory Tech.,47,1999,2075–2084. [47]Ramakrishna,S.A.and Pendry,J.B.,Spherical perfect lens:Solutions of Maxwell’s equations for spherical geometry,Phys.Rev.B,69,2004,115115. [48]Shelby,R.A.,Smith,D.R.and Schultz,S.,Experimental Verification of a Negative Index of Refraction,Science,292,2001,77–79. [49]Veselago,V.G.,The electrodynamics of substances with simultaneously negative values ofεand µ,Usp.Fiz.Nauk,92,1964,517–526.


2.1 An heuristic argument for Nicorovici,Mc Phedran and Milton’s result













2.2 Reflecting complementary med ia




















3 Superlensing Using Complementary Media






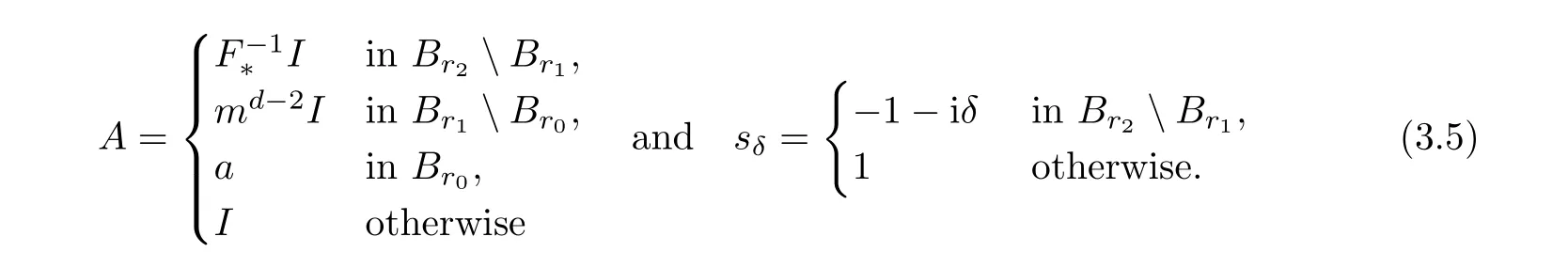








4 Cloaking Using Complementary Media






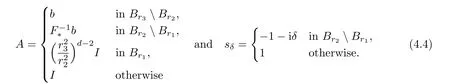











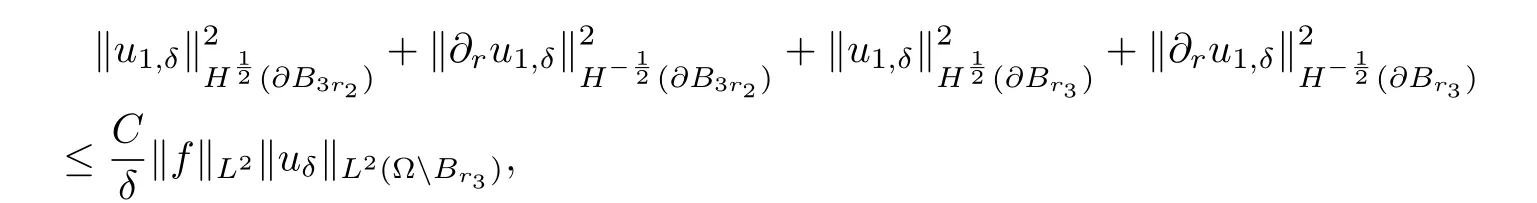







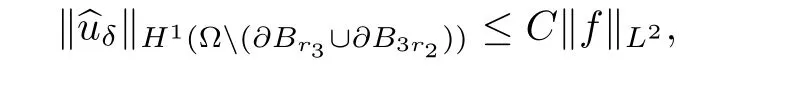
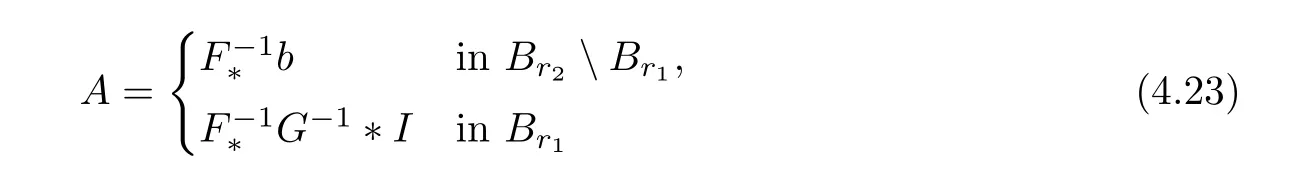
5 Cloaking a Source via Anomalous Localized Resonance


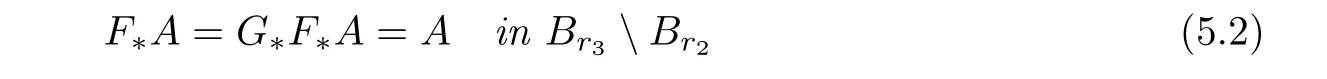





























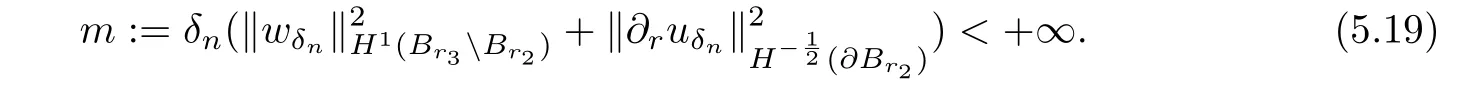










6 Limitting Absorption Principle and Well-Posedness of the Helmholtz Equation with Sign Changing Coefficients









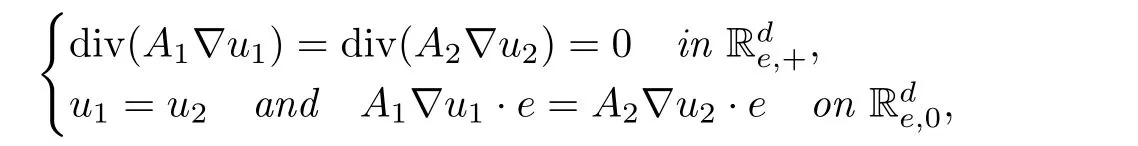

























杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- The Mathematical Theory of Multifocal Lenses∗
- Asymptotics and Blow-up for M ass Critical Nonlinear Disp ersive Equations∗
- Singular Solutions to Conformal Hessian Equations
- Convergence to a Single Wave in the Fisher-KPP Equation∗
- A Third Derivative Estimate for Monge-Ampere Equations with Conic Singularities
- CR Geometry in 3-D∗
