Paul C.YANG

(Dedicated to Professor Haim Brezis with admiration)

1 Introduction

A CR manifold is a pair(M2n+1,J)of a smooth oriented(real)(2n+1)-dimensional manifold together with a formally integrable complex structure J:H→H on a maximally nonintegrable codimension one subbundle H ⊂TM.In particular,the bundleis orientable and any nonvanishing section θ of E is a contact form,i.e.,θ ∧ (dθ)nis nonvanishing.We assume further that(M2n+1,J)is strictly pseudo-convex,meaning that the symmetric tensoris positive definite;since E is one-dimensional,this is independent of the choice of contact formθ.

Given a CR manifold(M2n+1,J),we can define the subbundle T1,0of the complexified tangent bundle as the+i-eigenspace of J,and T0,1as its conjugate.We likewise denote byΛ1,0the space of(1,0)-forms(that is,the subbundle ofwhich annihilates T0,1)and byΛ0,1its conjugate.The CR structure is said to be integrable if T0,1is closed under the Lie bracket,a condition that is vacuous when n=1.The canonical bundle K is the complex line-bundle K= Λn+1(Λ1,0).

A pseudohermitian manifold is a triple(M2n+1,J,θ)of a CR manifold(M2n+1,J)together with a choice of contact form θ.The assumption that dθ(·,J·)is positive definite implies that the Levi formdefined on T1,0is a positive-definite Hermitian form.Since another choice of contact formis equivalent to a choice of(real-valued)function σ∈C∞(M)such thatand the Levi forms of bθandθare related bywe see that the analogy between CR geometry and conformal geometry begins through the similarity of choosing a contact form or a metric in a conformal class(see[17]).

Given a pseudohermitian manifold(M2n+1,J,θ),the Reeb vector field T is the uniquevector field such thatθ(T)=1 and dθ(·,T)=0.An admissible coframe is a set of(1,0)-forms{θα}nα=1whose restriction to T1,0forms a basis forand such that θα(T)=0 for allα.Denote bythe conjugate ofθα.Thenfor some positive definite Hermitian matrixDenote bythe frame for TCM dual toso that the Levi form is

Tanaka[35]and Webster[38]defined a canonical connection on a pseudohermitian manifold(M2n+1,J,θ)as follows:Given an admissible coframe{θα},define the connection forms ωαβand the torsion form τα=Aαβθβby the relations

where we use the metricto raise and lower indices,In particular,the connection forms are pure imaginary.The connection forms define the pseudohermitian connection on T1,0by,which is the unique connection preserving T1,0,T,and the Levi form.

The curvature formcan be written as

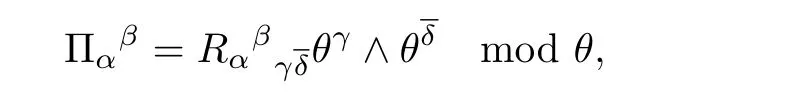
defining the curvature of M.The pseudohermitian Ricci tensor is the contractionand the pseudohermitian scalar curvature is the contractionAs shown by Webster[38],the contractionis given by

For computational and notational efficiency,it is usually more useful to work with the pseudohermitian Schouten tensor

and its traceThe following higher order derivatives:

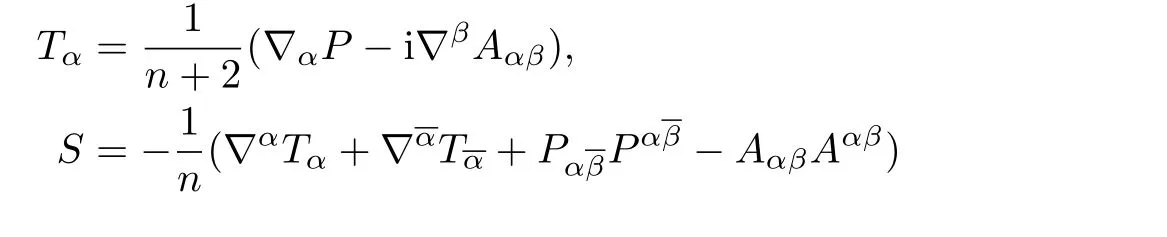
also appear frequently(see[19,30]).

In performing computations,we usually use abstract index notation,so for exampleταdenotes a(1,0)-form and ∇α∇βf denotes the(2,0)-part of the Hessian of a function.Of course,given an admissible coframe,these expressions give the components of the equivalent tensor.The following commutator formulas are useful.

Lemma 1.1

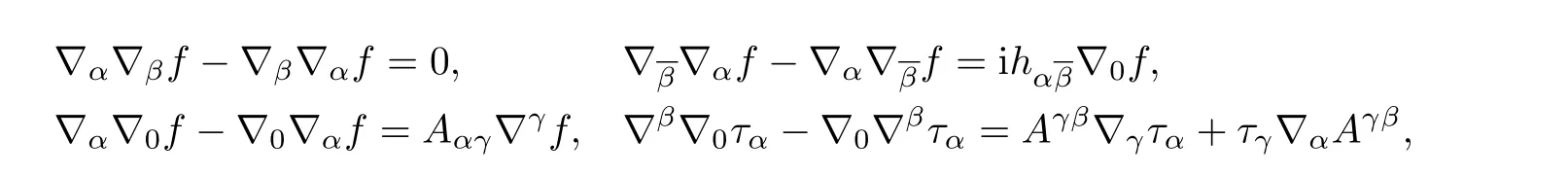
where∇0denotes the derivative in the direction T.

The following consequences of the Bianchi identities are also useful.

Lemma 1.2

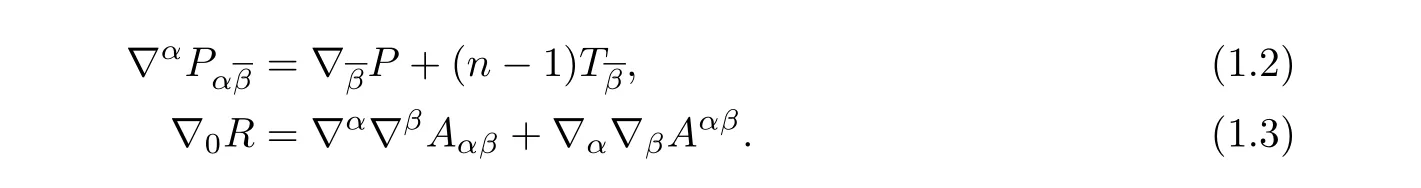
In particular,

An important operator in the study of pseudohermitian manifolds is the sublaplacian

Defining the subgradient∇bu as the projection of d u onto H∗⊗C(that is,it is easy to show that

for any u,v ∈ C∞(M),at least one of which is compactly supported,and where ⟨·,·⟩denotes the Levi form.

One important consequence of the Bianchi identity is that the operator P has the following two equivalent forms:

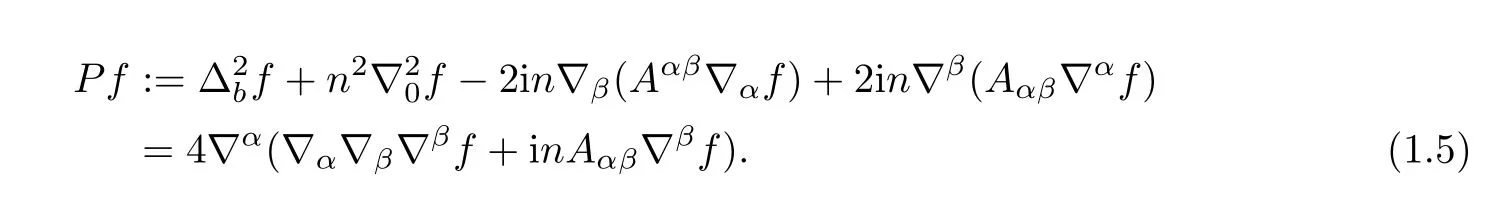
In dimension n=1,the operator P is the compatibility operator found by Graham and Lee[22].Hirachi[24]later observed that in this dimension P is a CR covariant operator,in the sense that it satisfies a particularly simple transformation formula under a change of contact form.Thus,in this dimension P is the CR Paneitz operator P4.

1.1 CR pluriharmonic functions

Given a CR manifold(M2n+1,J),a CR pluriharmonic function is a function u∈C∞(M)which is locally the real part of a CR function v∈C∞(M;C),i.e.,u=Re(v)for v satisfyingWe denote by P the space of pluriharmonic functions on M,which is usually an infinite-dimensional vector space.When additionally a choice of contact formθisgiven,Lee[31]proved the following alternative characterization of CR pluriharmonic functions which does not require solving for v.

Proposition 1.1Let(M2n+1,J,θ)be a pseudohermitian manifold.A function u∈C∞(M)is CR pluriharmonic if and only if

It is straightforward to check that(see[22])

In particular,we see that the vanishing ofimplies the vanishing of Pαu when n>1.Moreover,the conditionis vacuous when n=1,and by(1.6),we can consider the condition Pαu=0 from Proposition 1.1 as the “residue” of the condition

Note also that,using the second expression in(1.5),we have that P=4∇αPα.In particular,it follows that P⊂ker P4for three-dimensional CR manifolds(M3,J).It is easy to see that this is an equality when(M3,J)admits a torsion-free contact form(see[22]),the general case is a question of interest that will be addressed in Section 3.

The space of CR pluriharmonic functions is stable for the one-parameter family(M3,Jt,θ)of pseudohermitian manifold if for everyφ∈Ptand everyε>0,there is aδ>0 such that for each s satisfying|t−s|< δ,there is a CR pluriharmonic function fs∈Pssuch that

We also discuss the question of stability in Section 3.

2 The Embedding Problem

The typical examples of CR structure are the smooth boundaries of strictly pseudo-convex complex manifolds.LetΩbe a smooth strictly pseudo-convex domain in a Stein manifold given by a defining function u<0 which satisfies the nondegeneracy condition at the boundaryΣ={u=0},and u is strictly plurisubharmonic nearΣ.Then one easily verifies thatrestricts to a contact form onΣ,and kerθ=ξinherits the ambient almost complex structure J.The converse question whether every CR structure arises this way is known as the embedding problem.In dimensions 2n+1≥5,this was answered affirmatively by the work of Boutet de Monvel[1].The special case n=1 has received a good deal of attention since the work of Rossi[34]and is the focus of this section.

The example of Rossi is a small perturbation of the standard CR 3-sphere:Let S3=be the boundary of the unit ball in C2.The standard CR structure is given by the vector fieldConsider for each t the new CR structure given byFor 0<|t|<1,it is shown by Burns[4]that the CR holomorphic functions must be even functions,hence this CR structure cannot be realized in CNfor any N.In this same paper it is shown that if for a given CR structure in 3-D,the CR holomorphic functions separate points and the Szego projection is continuous in the C∞topology,then the structure may be realized in some CN.In[29],Kohn showed that these conditions are indeed satisfied if theoperator on functions has closed range.Subsequently,Lempert[32]showed that when the torsion vanishes a CR structure in 3-D may be realised in Cn.We note the vanishing torsion condition means that the Reeb vector field generates a one parameter family of biholomorphic transformations of the CR structure.

In order to relax the condition of vanishing torsion,one realizes that the Paneitz operator plays an important role in the embedding question.

Theorem 2.1(see[12])If(M3,θ,J)satisfy the condition P4≥ 0 and the Webster scalar curvature R≥c>0,then the nonzero eigenvaluesλof the operatorsatisfy the lower bound λ≥min R.As a consequence,theoperator has closed range.

It is helpful to remark that the vanishing torsion condition implies the condition P4≥0:This follows from the two identities involving the Paneitz operator and theoperator:

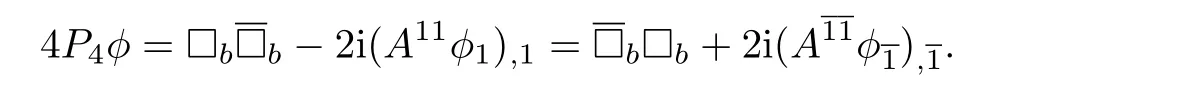
Thus when torsion vanishes,commutes withand hence P4≥0.

As a consequence of this eigenvalue bound,it is possible to verify the stability of embedding for a family of CR structures{Jt||t|< ϵ}on a given(M3,ξ)satisfying the same assumptions as in Theorem 2.1.If the CR structure J0is embeddable in CN,then for t sufficiently small,there is an embedding of Jtwhich is close to that for J0.

In the next section,we discuss the natural questions of positivity of Paneitz operator which is closely related to the stability question.

3 When is P4 Non-negative?

To find criteria to verify when P4is non-negative,one would like to know if CR manifolds embedded in C2with some additional nice properties satisfy these nonnegativity conditions assumed in Theorem 2.1.Working in this direction,[13]showed that these nonnegative conditions hold for small deformations of a strictly pseudo-convex hypersurface with vanishing torsion in

Another closely related question concerning the CR Paneitz operator is the identification of its kernel.It follows from its definition that,on a three-dimensional CR manifold,the space of CR pluriharmonic functions is contained in the kernel of the CR Paneitz operator.Moreover,Graham and Lee showed[22]that if a three-dimensional CR manifold admits a torsion-free contact form,then the kernel of the CR Paneitz operator consists solely of the CR pluriharmonic functions.One would like to characterize CR manifolds for which this equality holds.Since there are known non-embedded examples for which the equality does not hold,we restrict our attention to embedded CR manifolds.Motivated by this problem,Hsiao[26]showed that for embedded CR manifolds,there is a finite-dimensional vector space W,such that the kernel of the CR Paneitz operator P4splits into a direct sum:

There is an elementary proof of this fact in[8].

Theorem 3.1(see[8])Let(M3,Jt,θ)be a family of embedded CR manifolds for t∈ [−1,1]with the following properties:

(1)Jtis real analytic in the deformation parameter t.

(2)The Szegö projectorsvary continuously in the deformation parameter t(F2,0denotes the L2sections of the canonical bundle).

(3)For the structure J0we haveand kerthe space of CR pluriharmonic functions with respect to J0.

(4)There is a uniform constant c>0 such that

(5)The CR pluriharmonic functions are stable for the family(M3,Jt,θ).Thenand kerfor all t∈ [−1,1].

Remark 3.1The assumption(3.2)can be replaced by the assumption that the CR Yamabe constants Y[Jt]are uniformly positive.Since the assumptions on the CR Paneitz operator are CR invariant(see[24]),this allows us to recast Theorem 3.1 in a CR invariant way.

As an application,consider the family of ellipsoids in C2as deformations of the standard CR three-sphere.The formula established in[28,Theorem 1]expressing the Szegö kernel in terms of the defining function implies that condition(2)holds.Since the standard contact form on the CR three-sphere is torsion-free,its CR Paneitz operator is nonnegative and has kernel consisting only of the CR pluriharmonic functions(see[22]).An elementary calculation(see[13])shows that the ellipsoids have positive Webster scalar curvature thus verifying condition(4)of the theorem.The condition(5)then follows from the stability result of[12].Stability of CR functions for strictly pseudo-convex domains in C2first appeared in the work of Lempert[33].

Corollary 3.1The ellipsoids in C2are such that the Paneitz operator is nonnegative and has kernel consisting only of the CR pluriharmonic functions.

Theorem 3.1 shows that the stability of the CR pluriharmonic functions plays a role in preventing the existence of the supplementary space.If one wishes to use deformations to exhibit examples of CR manifolds for which the supplementary space exists,one should thus look at unstable families.Indeed there are conditions which guarantee the existence of the supplementary space.

First,using the Baire Category theorem,one can show that generically the supplementary space exists.

Theorem 3.2(see[9])Let(M3,Jt,θ)be a family of embedded CR manifolds with t ∈[−1,1].Assume that the Szegö projectorvaries real analytically in the deformation variable t.Then

(2)The set

is a closed set with no accumulation points.In particular,F has no interior points and hence F is of the first category.

(3)The set

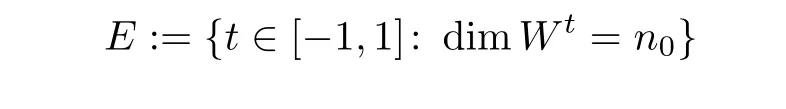
has nonempty interior.

Remark 3.2The theorem above states that for generic values t of the deformation parameter,dim Wt=n0.Since n0>0 if there exists a t0∈ [−1,1]withthe supplementary space exists for a generic value of t if it exists for some t0.Moreover,if n0>0,then dim Wt=0 for a thin set F ⊂ [−1,1]of the first category.

Under an assumption on the rate of vanishing of the first non-zero eigenvalue of the CR Paneitz operator for a family of CR structures,the loss of stability of the CR pluriharmonic functions implies the existence of the supplementary space.To make this precise,we list our assumptions.

Let(M3,Jt,θ)=:Mtbe a family of embedded CR manifolds for which Jtis C6in the deformation parameter t for some interval|t−t0|<µwithµ>0.Suppose that there is a constant c>0 independent of t,such that the following assertions hold.

(1)For anyand anyit holds that

whereas s tends to zero.

(2)For anyit holds that

Together,the assumptions(3.3a)and(3.3b)imply that the lowest nonzero absolute value of the eigenvalues of the CR Paneitz operatorjumps up

Next,we assume that there is a family of diffeomorphismswhich is C6in the deformation parameter t,such thatΦ0is the identity map.

Finally,we assume that the CR pluriharmonic functions are unstable at t0.More precisely,we assume that there is a CR pluriharmonic function f0∈C5for the structure M0and constants ε>0 and 0<δ<µ,such that for any t withand any CR pluriharmonic function ψ∈Pt,it holds that

Theorem 3.3(see[9])Assume that(M3,Jt,θ)is as described above.Then for allwith|t−t0|<δandδsufficiently small,the supplementary space Wtexists.

4 The Positivity of the CR M ass

An important application of the embedding theorem is the solvability of theequation,a key fact in the CR positive mass theorem.The situation is quite different from the positivity of mass in Riemannian geometry.

We consider a compact three-dimensional pseudohermitian manifold(M,J,θ)(with no boundary)of positive Tanaka-Webster class.This means that the first eigenvalue of the conformal sublaplacian

is strictly positive.Here∆bstands for the sublaplacian of M and R for the Tanaka-Webster curvature.The conformal sublaplacian has the following covarianceproperty under a conformal change of contact form:

where Q=4 is the homogeneous dimension of the manifold.The conformal sublaplacian rules the change of the Tanaka-Webster curvature under the above conformal deformation,through the following formula:

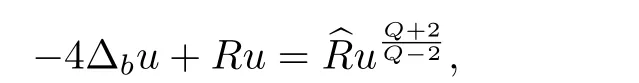
whereis the Tanaka-Webster curvature corresponding to the pseudohermitian structureThe positivity of the Tanaka-Webster class is equivalent to the condition

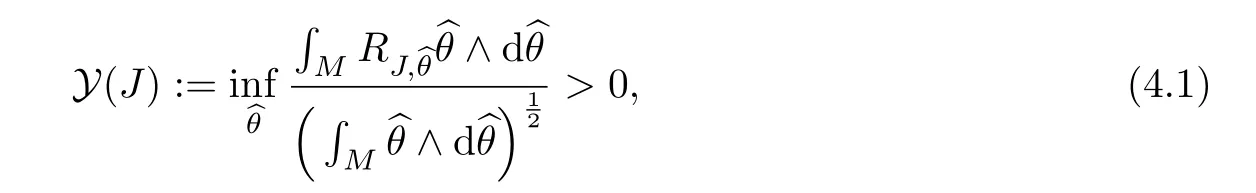
whereany contact form which annihilatesξ.Under the assumption Y(J)>0,we have that Lbis invertible,so for any p ∈ M,there exists a Green’s function Gpfor which

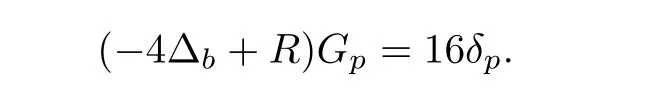
One can show that in CR normal coordinates(z,t),the Green’s function Gpadmits the following expansion:

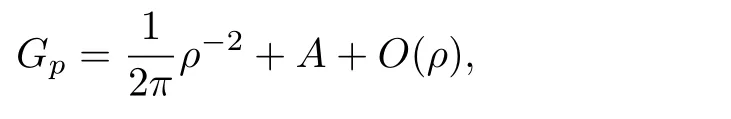
where A is some real constant and we have setρ4(z,t)=|z|4+t2,z∈C,t∈R.Analogous to the Riemannian construction for the blow-up of a compact manifold,we consider the new pseudohermitian manifold with a blow-up of contact form

With an inversion of coordinates,we then obtain a pseudohermitian manifold which has asymptotically the geometry of the Heisenberg group.Starting from this model,we give a definition of asymptotically flat pseudohermitian manifold and we introduce its pseudohermitian mass(p-mass)by the formula

where we setandstands for the connection form of the structure.The above quantity is indeed a natural candidate,since it satisfies the same property as the ADM mass in Riemannian geometry,and moreover it coincides with the zero-th order term in the expansion of the Green’s function for Lb.In the case that N arise as the blowup of M3,m is a positive multiple of the constant A.

[14]gave some general conditions which ensure the nonnegativity of the p-mass,characterizing also the zero case as(CR equivalent to)the standard three-dimensional CR sphere.

Theorem 4.1Let M be a smooth,strictly pseudo-convex three dimensional compact CR manifold.Suppose Y(J)>0,and that the CR Paneitz operator is nonnegative.Let p∈M and letθbe a blow-up of contact form as in(4.2).Then

(a)m(J,θ)≥ 0;

(b)if m(J,θ)=0,M is CR equivalent(or isomorphic as pseudohermitian manifold)to S3,endowed with its standard CR structure.

The assumptions here are conformally invariant,and are needed to ensure the positivity of the right-hand side in(4.3).The proof is patterned after the spinorial argument of Witten.By the embeddability result,the conditions on Y(J)and P imply the embeddability of M:We use this property to find a solution ofwith the correct asymptotics(to make the first term in the right-hand side of(4.3)vanish).

Hereis a function satisfying

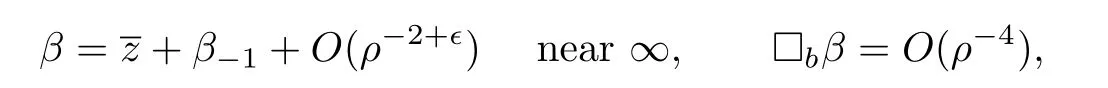
with β−1a suitable function with homogeneity −1 in ρ.

The full solvability ofthen reduces to a mapping theorem in weighted spaces worked out by Hsiao and Yung[27].

It is important to point out that the assumption P4≥0 is necessary,since there are small perturbations of the CR structure on the standard 3-sphere for which the CR mass is actually negative.Indeed it appears likely that this holds for generic perturbations of the standard 3-sphere.

5 Pseudo-Einstein Contact Forms

For strictly pseudo-convex domainsin Cn+1,Feff erman[16]introduced the following complex Monge-Ampere equation:

An iterative computational procedure is given to find approximate solutions of the equation(1.1)that is accurate to order n+1 near the boundary:Letψbe any smooth defining function of the boundary:

The resulting contact formsatisfies the following pseudo-Einstein condition:

Jack Lee[30]showed that the pseudo-Einstein condition is equivalent to the statement that at each point p∈M there exists a neighborhood of p in which there is a closed sectionωof the canonical bundle with respect to whichθis volume normalized,i.e.,

The special condition when n=1 is motivated by the observation that the Bianchi identity gives

There is a close connection of pseudo-Einstein contact forms with the pluriharmonic functions.Let(M3,J,θ)be a pseudohermitian manifold and define the(1,0)-form Wαby

Observe that Wαvanishes if and only ifθis pseudo-Einstein.As first,observed by Hirachi[24],Wαsatisfies a simple transformation formula;given another contact forma straightforward computation shows that

An immediate consequence of(5.2)is the following correspondence between pseudo-Einstein contact forms and CR pluriharmonic functions.

Proposition 5.1Let(M3,J,θ)be a pseudo-Einstein three-manifold.Then the set of pseudo-Einstein contact forms on(M3,J)is given by

Since there is a large supply of pseudo-Einstein contact form once there exists one,it is of interest to find a canonical one.Although the positive mass theorem provide a contact form that minimizes the CR Yamabe quotient,there is no assurance that it is pseudo-Einstein.In the next section,we introduce a new operator that is relevant to this question.

6 The P-Prime Operator

Using spectral methods,Branson,Fontana and Morpurgo[2]have recently identified a new operatoron the standard CR three-sphere(S3,J,θ0),such thatis of the formplus lower-order terms,is invariant under the action of the CR automorphism group of S3,andappears in an analogue of Q-curvature equation in which the exponential term is present.However,the operatoracts only on the space P of CR pluriharmonic functions on S3,namely those functions which are the boundary values of pluriharmonic functions in the ball{(z,w):|z|2+|w|2<1}⊂C2.The space of CR pluriharmonic functions on S3is it self invariant under the action of the CR automorphism group,so it makes sense to discuss the invariance ofUsing this operator,Branson,Fontana and Morpurgo[2]showed that

for all u ∈ P,whereand equality holds in(6.1)if and only if euθ0is a standard contact form.In[7],we extended the definition of P′to moregeneral CR structures in dimension n=1.

To describe our results,let us begin by discussing in more detail the ideas which give rise to the definitions ofand.To definewe follow the same strategy of Branson,Fontana,and Morpurgo[2].First,Gover and Graham[19]showed that on a general CR manifold(M2n+1,J),one can associate to each choice of contact formθa formally-self adjoint real fourth-order operator P4,nwhich has leading order termand that this operator is CR covariant.On three-dimensional CR manifolds,this reduces to the well-known operator

which,through the work of Graham and Lee[22]and Hirachi[24],is known to serve as a good analogue of the Paneitz operator of a four-dimensional conformal manifold.As pointed out by Graham and Lee[22],the kernel of P4(as an operator on a three-dimensional CR manifold)contains the space P of CR pluriharmonic functions,and thus one can ask whether the operator

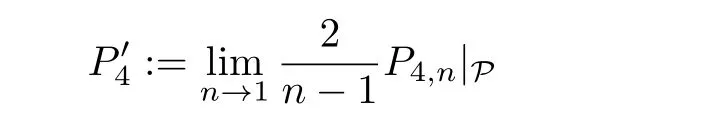
is well-defined.This is the case.It then follows from standard arguments(see[3])that ifis any other choice of contact form,then the corresponding operatoris related toby

for any f∈P.Thus the relation betweenand P4is analogous to the relation between the Q-curvature and the Paneitz operator.More precisely,the P′-operator can be regarded as a Q-curvature operator in the sense of Branson and Gover[3].Moreover,since the Paneitz operator is self-adjoint and kills pluriharmonic functions,the transformation formula(6.2)implies that

for any f∈P,returningto the status of a Paneitz-type operator.This is the sense in which the P′-operator is CR invariant,and is the way that it is studied in(6.1).

From its construction,one easily sees thatis exactly Hirachi’s Q-curvature.Thus,unlike the Paneitz operator,the P′-operator does not necessarily kill constants.However,there is a large and natural class of contact forms for which the P′-operator does kill constants,namely the pseudo-Einstein contact forms.In this setting,it is natural to ask whether there is a scalar invariantsuch thatIndeed,if(M3,J,θ)is a pseudo-Einstein manifold,then the scalar invariant

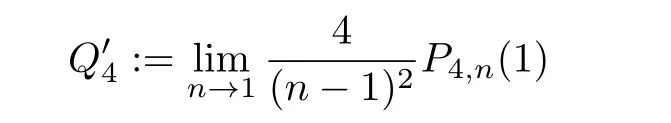
is well-defined.As a consequence,ifis another pseudo-Einstein contact form(in particular,σ∈P),then

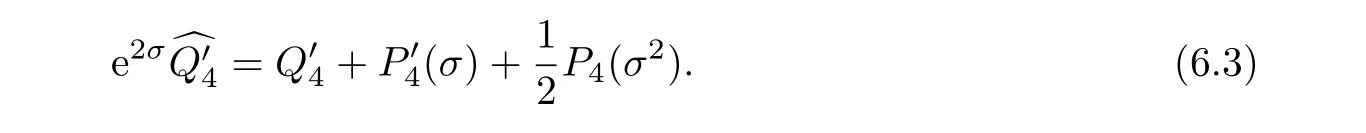
Taking the point of view thatis a Paneitz-type operator,we may also write

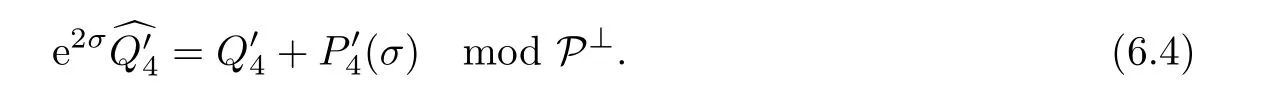
The upshot is that,on the standard CR three-sphere,so that this indeed recovers the interpretation of the Beckner-Onofri-type inequality(6.1)of Branson-Fontana-Morpurgo[2]as an estimate involving a Paneitz-type operator and Q-type curvature.Additionally,we also see from(6.3)that the integral ofis a CR invariant.More precisely,if(M3,J)is a compact CR three-manifold andare two pseudo-Einstein contact forms,then

In conformal geometry,the total Q-curvature plays an important role in controlling the topology of the underlying manifold.For instance,the total Q-curvature can be used to prove sphere theorems(see,e.g.,[23,Theorem B]and[11,Theorem A]).We have the following CR analogue of Gursky’s theorem[23,Theorem B].

Theorem 6.1Let(M3,J,θ)be a compact three-dimensional pseudo-Einstein manifold with nonnegative Paneitz operator and nonnegative CR Yamabe constant.Then

with equality if and only if(M3,J)is CR equivalent to the standard CR three sphere.

The proof of Theorem 6.1 relies upon the existence of a CR Yamabe contact form,that is,the existence of a smooth unit-volume contact form with constant Webster scalar curvature equal to the CR Yamabe constant(see[14]).In particular,it relies on the CR Positive Mass theorem(see[14]).One complication which does not arise in the conformal case(see[23])is the possibility that the CR Yamabe contact form may not be pseudo-Einstein.We overcome this difficulty by computing how the local formula fortransforms with a general change of contact form,i.e.,without imposing the pseudo-Einstein assumption.

In conformal geometry,the total Q-curvature also arises when considering the Euler characteristic of the underlying manifold.Burns and Epstein[5]showed that there is a biholomorphic invariant,now known as the Burns-Epstein invariant,of the boundary of a strictly pseudoconvex domain which is related to the Euler characteristic of the domain in a similar way.It turns out that the Burns-Epstein invariant is a constant multiple of the total Q′-curvature,and thus there is a nice relationship between the total Q′-curvature and the Euler characteristic.

Theorem 6.2Let(M3,J)be a compact CR manifold which admits a pseudo-Einstein contact form θ,and denote by µ(M)the Burns-Epstein invariant of(M3,J).Then

In particular,if(M3,J)is the boundary of a strictly pseudo-convex domain X,then

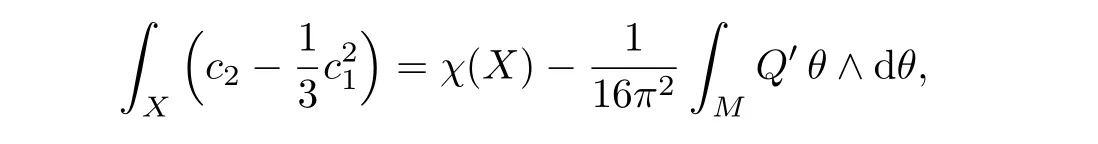
where c1and c2are the first and second Chern forms of the Kähler-Einstein metric in X obtained by solving Fefferman’s equation,and χ(X)is the Euler characteristic of X.

In general dimensions,the existence of P′operators is given by Hirachi[25]and described in terms of tractor calculus by Case-Gover in a forthcoming publication.

7 An Extremal Pseudo-Einstein Contact Form

In pursuing the analogy with the pair(P4,Q4)in conformal geometry,it is more natural to focus on the operatorwhich is given byτ◦P′where τ is the projection to the pluriharmonics.Similarly,it is morenatural to consider the scalar invariantThe transformation property ofimplies that if bθ=ewθare both pseudo-Einstein,then equation(6.4)showed thathave the same formal properties as(P4,Q4).Note that if θ is pseudo-Einstein,thenis pseudo-Einstein if and only if w∈P[24],so that(6.2)makes sense.

We will construct contact forms for which the Q′-curvatureis constant by constructing minimizers of the II-functional given by

on a pseudo-Einstein three-manifold(M3,T1,0M,θ).Note that,since II is only defined on w,the projections in(7.1)can be removed,i.e.,we can equivalently define the II-functional in terms ofand.In general,the II-functional is not bounded below.However,under natural positivity conditions,it is bounded below and coercive,in which case we can construct the desired minimizers.

Theorem 7.1(see[6])Let(M3,T1,0M,θ)be a compact pseudo-Einstein three-manifold,such that the P′-operatornonnegative and kerSuppose additionally that

Then there exists a function w∈P which minimizes the II-functional(7.1).Moreover,the contact formis such thatis constant.

Some comments on the statement of Theorem 7.1 are in order.First,[7]provided some sufficient condition for the operatorto be non-negative.Second,the assumptions of the theorem are all CR invariant:The assumptions onare independent of the choice of contact form and the assumption(7.2)is independent of the choice of pseudo-Einstein contact form.In particular,if one is interested only in boundaries of domains in C2,the assumptions are biholomorphic invariants.Third,the assumption that P′is nonnegative with trivial kernel(i.e.,kerautomatically holds if there exists a pseudo-Einstein contact form with nonnegative scalar curvature(see[7]).Fourth,the assumption(7.2)holds if one assumes instead that(M3,T1,0M,θ)has nonnegative CR Paneitz operator and nonnegative CR Yamabe constant(see[7]).Note here that 16π2is the total Q′-curvature of the standard CR three-sphere.Fifth,the conclusion thatconstant is the best that one can hope for:Though it is tempting to speculate that minimizers of the II-functional actually give rise to contact forms for whichis constant,as happens on the standard CR three-sphere,the natural structure on S1×S2is an example where there is a unique,up to homothety,contact form for whichis constant butis nonconstant.

The proof of Theorem 7.1 is analogous to the corresponding result for the Q-curvature in four-dimensional conformal geometry(see[10]),though there are many new difficulties,we must overcome.Since we are minimizing within P,there is a Lagrange multiplier in the Euler equation for the II-functional which lives in the orthogonal complement P⊥to P.Rather than obtain estimates on the Lagrange multiplier,we establish regularity of minimizers by studying the Green’s function ofThe greater difficulty lies in showing that minimizers infor the II-functional exist under the hypotheses of Theorem 7.1.The basic idea here is to use the positivity ofand(7.2)to show that the II-functional is coercive.However,doing so requires showing thatsatisfies a Moser-Trudinger inequality with the same constant as on the CR three-sphere.We do this by appealing to the general results of Fontana and Morpurgo[18],which depends upon having a fairly detailed understanding of the properties ofThis is technically the most involved part of the argument.

8 An Isoperimetric Inequality

The Q′curvature integral has in addition to its topological meaning,an analytic consequence as an invariant that controls the isoperimetric constant for a class of pseudo-Einstein contact forms.

Consider the Heisenberg group H1which may berealized as{(x,y,t)∈R3}with the contact form θ0=d t+x d y −y d x and the CR structure given byBoth curvature and torsion vanish hence it is pseudo-Einstein.Consider bθ=e2uθwhereσ∈P.The P′operator is simply given by P′=(∆b)2,and one checks easily that P′maps P to itself,so that there is no need to project back to P.

We make three remarks concerning this bound.First,this result is a weak analogue of the stronger result in conformal geometry(see[36]).Second,the isoperimetric constant only depends on the size of the Q′-curvature integral.Third,the constant c1is the constant appearing in the following integral representation formula to be established for such u:

AcknowledgementsThe author takes this opportunity to thank his collaborators who provide inspiration and support in these investigations:Jeffrey Case,Sagun Chanillo,Jih-Hisn Cheng,Hung-Lin Chiu,Rod Gover,Chin-Yu Hsiao,Andrea Malchiodi,Yi Wang and Polam Yung.

[1]Boutet de Monvel,L.,Integration des Equations de Cauchy-Riemann Induites Formelles,Seminaire Goulaouic-Lions-Schwartz,1974–1975.

[2]Branson,T.P.,Fontana,L.and Morpurgo,C.,Moser-Trudinger and Beckner-Onofri’s inequalities on the CR sphere,Ann.of Math.(2),177(1),2013,1–52.

[3]Branson,T.P.and Gover,R.,Conformally invariant operators,differential forms,cohomology and a generalisation of Q-curvature,Comm.Partial Differential Equations,30,2005,1611–1669.

[4]Burns,D.,Global behavior of sometangential Cauchy-Riemann equations,Proceedings Conf.Park City,Utah,1977,Dekker,New York,1979,51–56.

[5]Burns,D.and Epstein,C.,A global invariant for three dimensional CR-manifolds,Invent.Math.,92,1988,333–348.

[6]Case,J.,Hsiao,C.Y.and Yang,P.C.,Extremal metrics for the Q′-curvature in three dimensions,2015,preprint.

[7]Case,J.and Yang,P.C.,A Paneitz-type operator for CR pluriharmonic functions,Bull.Inst.Math.Acad.Sinica,8,2013,285–322.

[8]Case,J.,Chanillo,S.and Yang,P.C.,The CR Paneitz operator and the stability of CR pluriharmonic functions,Advances in Math.,to appear.

[9]Case,J.,Chanillo,S.and Yang,P.C.,A remark on the kernel of the Paneitz operator.http://dx.doi.org/11.1016/j.na.2015.04.001

[10]Chang,S.Y.A.and Yang,P.C.,Extremal metrics of zeta function determinants on 4-manifolds,Annals Math.,142,1995,171–212.

[11]Chang,S.Y.A.,Gursky,M.and Yang,P.C.,A conformally invariant sphere theorem in four dimensions,Pub.IHES,98,2003,105–143.

[12]Chanillo,S.,Chiu,H.-L.and Yang,P.C.,Embeddability for 3-dimensional Cauchy-Riemann manifolds and CR Yamabe invariants,Duke Math.J.,161,2012,2909–2921.

[13]Chanillo,S.,Chiu,H.-L.and Yang,P.C.,Embedded three-dimensional CR manifolds and the nonnegativity of Paneitz operators,Geometric Analysis,Mathematical Relativity,and Nonlinear Partial Differential Equations,Vol.599 of Contemp.Math.,65–82.Amer.Math.Soc.,Providence,RI,2013.

[14]Cheng,J.-H.,Malchiodi,A.and Yang,P.C.,A positive mass theorem in three dimensional Cauchy-Riemann geometry,2013,preprint.

[15]Cheng,J.-H.,Hwang,J.-F.,Malchiodi,A.and Yang,P.C.,Minimal surfaces in pseudohermitian geometry,Annali Scuola Norm.Sup.Pisa,2005,129–177.

[16]Fefferman,C.,Monge-Ampere equations,the Bergman kernel,and geometry of pseudoconvex domains,Ann.of Math.,103,1976,395–416.

[17]Fefferman,C.and Hirachi,K.,Ambient metric construction of Q-curvatures in conformal and CR geometry,Math.Res.Lett.,10,2003,819–831.

[18]Fontana,L.and Morpurgo,C.Adams inequality on measure spaces,Adv.Math.,226,2011,5066–5119.

[19]Gover,A.R.and Graham,C.R.,CR invariant powers of the sub-Laplacian,J.Reine Angew.Math.,583,2005,1–27.

[20]Gover,A.R.and Peterson,L.J.,The ambient obstruction tensor and the conformal deformation complex,Pacific J.Math.,226(2),2006,309–351.

[21]Graham,C.R.,Compatibility operators for degenerate elliptic equations on the ball and Heisenberg group,Math.Z.,187(3),1984,289–304.

[22]Graham,C.R.and Lee,J.M.,Smooth solutions of degenerate Laplacians on strictly pseudoconvex domains,Duke Math.J.,57(3),1988,697–720.

[23]Gursky,M.,The principal eigenvalue of a conformally invariant differential operator,with an application to semilinear elliptic PDE,Comm.Math.Phys.,207,1999,131–143.

[24]Hirachi,K.,Scalar pseudo-Hermitian invariants and the Szegö kernel on three-dimensional CR manifolds,Complex Geometry Osaka,1990,Lecture Notes in Pure and Appl.Math.,143,67–76.Dekker,New York,1993.

[25]Hirachi,K.,Q-prime curvature on CR manifolds,preprint.ar Xiv:1302.0489

[26]Hsiao,C.-Y.,On CR Paneitz operators and CR pluriharmonic functions,preprint.ar Xiv:1405.0158

[27]Hsiao,C.-Y.and Yung,P.,Solving Kohn Laplacian on asymptotically flat pseudohermitian 3-manifolds,2013,preprint.

[28]Kerzman,N.and Stein,E.M.,The Szego kernel in terms of Cauchy-Fantappie kernels,Duke Math.J.,45,1978,197–224.

[29]Kohn,J.J.,The range of the tangential Cauchy Riemann operator,Duke Math.J.,53,1986,525–545.

[30]Lee,J.M.,The Fefferman metric and pseudo-hermitian invariants,Trans.Amer.Math.Soc.,296,1986,411–429.

[31]Lee,J.M.,Pseudo-Einstein structures on CR manifolds,Amer.J.Math.,110,1988,157–178.

[32]Lempert,L.,On three-dimensional Cauchy-Riemann manifolds,J.Amer.Math.Soc.,5,1992,923–969.

[33]Lempert,L.,Embeddings of three dimensional Cauchy Riemann manifolds,Math.Ann.,300(1),1994,1–15.

[34]Rossi,H.,Attaching analytic spaces to an analytic space along a pseudoconvex boundary,Proceedings of the Conference on Complex Analysis(Minneapolic,1964).Springer-Verlag,Berlin,1965,242–256.

[35]Tanaka,N.,A differential geometric study on strongly pseudo-convex manifolds,Lectures in Mathematics,Department of Mathematics,Kyoto University,No.9,Kinokuniya Book-Store Co.,Ltd.,Tokyo,1975.

[36]Wang,Y.,Isoperimetric inequality,Q-curvature and Apweights,Advances in Math.,2013,to appear.

[37]Wang,Y.and Yang,P.C.,Isoperimetric inequality on CR manifolds,2015,preprint.

[38]Webster,S.M.,Pseudo-Hermitian structures on a real hypersurface,J.Differential Geom.,13(1),1978,25–41.