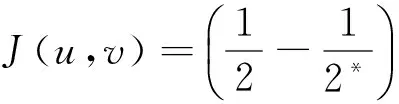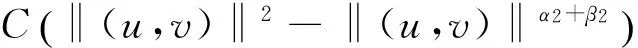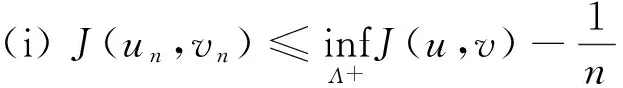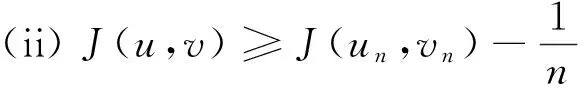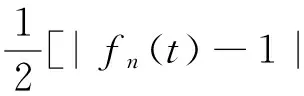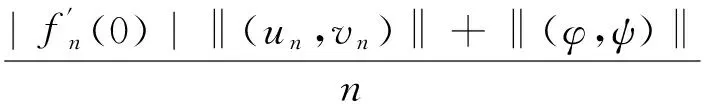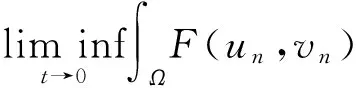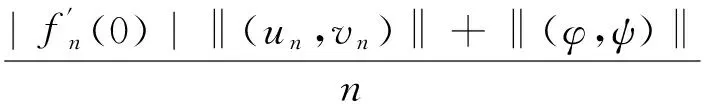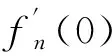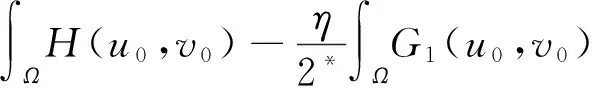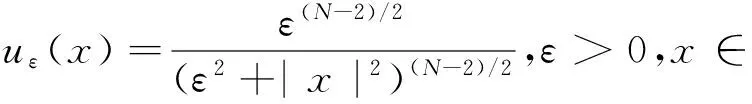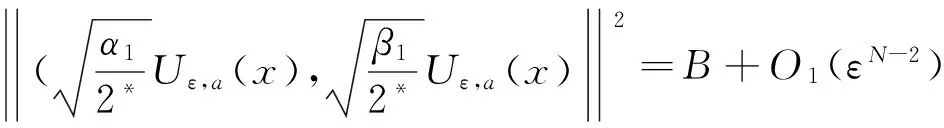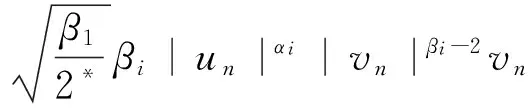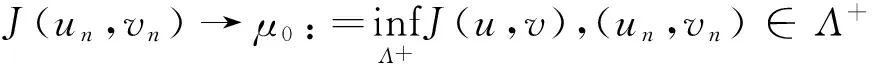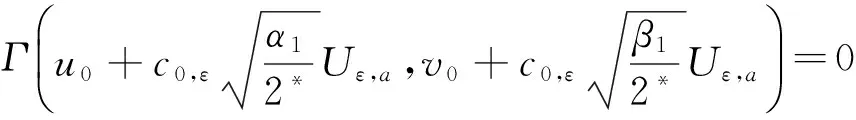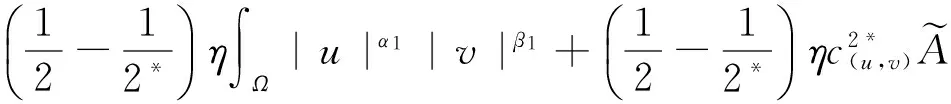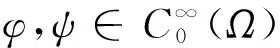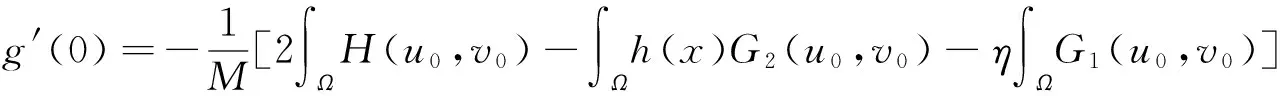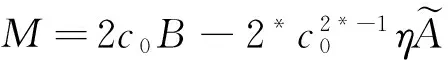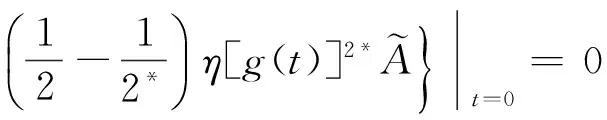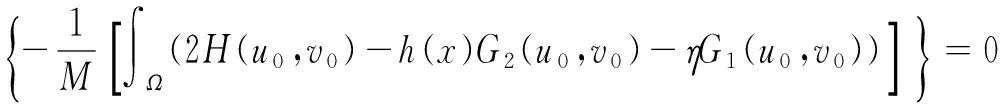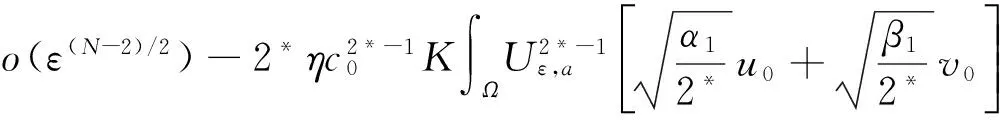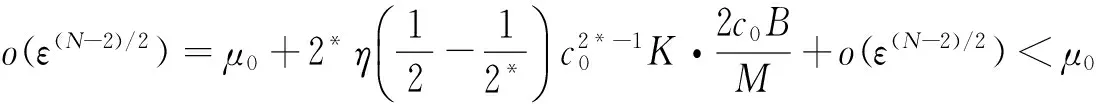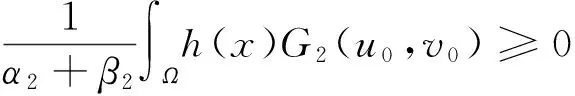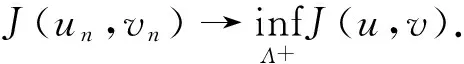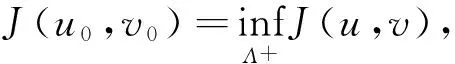一类带有负指数的临界椭圆方程组的解
2017-06-28康东升徐良顺曹玉平
康东升,徐良顺,曹玉平
(1 中南民族大学 数学与统计学学院,武汉 430074; 2 中南民族大学 图书馆,武汉 430074)
一类带有负指数的临界椭圆方程组的解
康东升1,徐良顺1,曹玉平2
(1 中南民族大学 数学与统计学学院,武汉 430074; 2 中南民族大学 图书馆,武汉 430074)
研究了一类带有强耦合临界非线性项和负指数项的椭圆方程组.定义了几个重要的约束集,运用复杂的分析技巧研究了能量泛函在约束集的下确界,得到了一个临界常数的精确表达式,最后证明了一定条件下方程组正解的存在性,首次把单个临界椭圆方程的相关结果推广到了带有负指数项的临界椭圆方程组.
椭圆方程组;临界非线性项;负指数项;变分法
1 相关知识
在本文中, 研究如下方程组:
(1)
(H1)η>0,α1,β1>0,i=1,2,α1+β1=2*,α2+β2<2,h(x)∈L∞(Ω).
存在一个常数α满足α≥max{1-a2,1-β2},m>0,M>0, 使得:

由于min{α2,β2}∈(0,1),所以J∈C(H×H,).如果(u,v)∈H×H并且u,v>0 a.e.于Ω中,对所有(φ,ψ)∈H×H满足:
0=∫Ω(uφ+vφφ,
(2)
则称(u,v)是方程组(1)的一组解.
用D:=D1,2(N) 表示(N)在范数下的完备化空间.对所有的α,β∈(0,2*)满足α+β=2*,基于Sobolev不等式和Young不等式,可以定义下面这两个最佳常数[1,2]:
(3)
Talenti在文[2]中证明了Sobolev常数S有如下达到函数:

(4)

方程组(1)主要是受到如下椭圆问题的启发:
(5)
其中λ≥0,γ>0,1 设(u,v)∈H×H,定义H×H上的范数‖(u,v)‖2:=∫Ω(|u|2+|v|2)dx. 因为J∉C1(H×H,),定义如下的约束集:, 其中Γ(u,v)=‖(u,v)‖2-η∫Ω|u|α1|v|β1dx-∫Ωh(x)|u|α2|v|β2dx. I(u,v):=(2-2*)‖(u,v)‖2+(2*-α2-β2)∫Ωh(x)|u|α2|v|β2dx. Λ+:={(u,v)∈Λ|I(u,v)>0},Λ0:={(u,v)∈Λ|I(u,v)=0},Λ-:={(u,v)∈Λ|I(u,v)<0}. 本文的主要结论如下. 定理 1 假设条件(H1)成立,并且η<η1. 则方程组(1)至少有一个解. 在接下来的讨论中,先给出两个引理及其证明,之后再证明定理1.当t>0, 用O(εt)来表示满足|O(εt)|/εt≤C的变量,这里C是正常数,用o(εt)表示满足当ε→0时|o(εt)|/εt→0的变量;为方便将省略积分式中的dx. 对所有(u,v)∈Λ,有: 这说明泛函J在Λ中是强制的并且有下界,因此可以考虑下面两个下确界问题: (6) 通过对Φ(t,u,v)的性质的研究,发现J(tu,tv)在[t-(u,v),t+(u,v)]上是单调递增的,对所有的(u,v)∈Λ-,有t+(u,v)=1,并且: J(t+(u,v)u,t+(u,v)v)≤J(u,v), (7) 为此选择满足下列两个性质的极小化序列{(un,vn)}⊂Λ+, (8) v-vn)‖,∀(u,v)∈Λ+. (9) 由于J(u,v)=J(|u|,|v|),所以un,vn是径向对称的,假设u0,v0≥0.因为(un,vn)在H×H是有界的,所以(un,vn)在H×H中弱收敛于(u0,v0).因此可以通过研究序列{(un,vn)}来获得有关(u0,v0)的性质,进一步证明(u0,v0)是问题(1)的一个解. 为了叙述的方便,定义下面几个记号: Gi(u,v)=αi|u|αi-2|v|βiuφ+ βi|u|α1|v|βi-2vψ,i=1,2, |u|α2|v|β2), 其中φ,ψ∈C∞(Ω). 引理1 如果(φ,ψ)∈H×H,则下面的不等式成立: J(u0,v0),(φ,ψ)≥0. (10) 将上式除以t>0,并对变量t取极限,得到: 又注意到: 假设e1是方程Δe1+λ1e1=0,x∈Ω,e1|∂Ω=0的第一特征函数;取φ=ψ=e1作为检验函数,又un(x),vn(x)>0,所以: (11) 因此引理1成立. 令: 由文献[1]可知函数对: 引理2 如果η∈(0,η1),则(u0,v0)∈Λ. 证明 记a0=Γ(u0,v0) ,令u0=φ,v0=ψ,由(11)式可知,a0≥0,为了证明a0=0,不妨假设a0>0.在该假设下,可以找到一个正数c0>0,使得: 另一方面,有: 由文献[8],得到下面两个重要的结果, (i)可以找到一个常数c0,ε=c0+δε,其中δε→0,当ε→0时,使得: (12) (ii)下面这个等式成立: 由此可以推得,(u0,v0)是下面泛函的局部极值函数对: (13) 这表明g′(0)存在且: (14) (15) ∫Ωu0Uε,a=O(ε(N-2)/2), (16) o(ε(N-2)/2), (17) o(ε(N-2)/2). (18) 由于h(x)|u0|α2|v0|β2∈L∞(Ω),利用中值定理,有: 将上列估计式(16)~(18)应用到(12)式中得: 推得: 又由(15)式推得: (-δε)= (19) 且知δε=O(ε(N-2)/2),由于a0>0,显然有: (20) 又注意到: 定理1的证明 令φ,ψ∈H, ε>0,定义: Φ=(u0+εφ)+, Ψ=(v0+εψ)+,(Φ,Ψ)∈H×H, Ω1={x|u0+εφ>0}, Ω2={x|v0+εψ>0},Ω-=Ω-Ω1∩Ω, 所以Φ(x)=u0+εφ|Ω1,Ω2=v0+εψ|Ω2,由引理2及不等式(11)可得: (21) 显然,当ε→0时,Ω-={x|u0+εφ≤0,v0+εψ≤0,x∈Ω}的测度亦趋向于0,由此可知∫Ω(u0φ+v0ψ)→0.将(21)式除以ε并对ε取极限,可得: [1] Alves C, Filho D, Souto M. On systems of elliptic equations involving subcritical or critical Sobolev exponents[J]. Nonlinear Analysis, 2000, 42: 771-787. [2] Talenti G. Best constant in Sobolev inequality[J]. Annali di Matematica Pura ed Applicata, 1976, 110(1): 353-372. [3] Chen Y, Chen J. Existence of multiple positive weak solutions and estimates forextremal values to a class of elliptic problems with Hardy terms and singular nonlinearity[J]. Journal of Mathematical Analysis and Applications, 2015, 492: 873-900. [4] Chen J, Rocha E. Positive solutions for elliptic problems with critical nonlinearity and combined singularity [J]. Mathematica Bohemica, 2010, 135: 413-422. [5] Lazer A, Mckenna P. On a singular nonlinear elliptic boundary value problem[J]. Proceedings of the American Mathematical Society, 1991, 111: 720-730. [6] Sun Y, Wu S, Long Y. Combined effects of singular and superlinear nonlinearities in some singular boundary value problems[J]. Journal of Differential Equations, 2001, 176: 511-531. [7] Tarantello G. On nonhomogenous elliptic equations involving critical Sobolev exponent[J]. Annales de l′Institut Henri Poincare Analyse Non Lineaire, 1992, 9(3): 281-304. [8] Sun Y, Zhang D. The role of the power 3 for elliptic equations with negative exponents[J]. Calculus Variations Partial Differential Equations, 2014, 49: 909-922. [9] 康东升,黄 燕,刘 殊. 一类拟线性椭圆问题极值函数的渐近估计[J]. 中南民族大学学报(自然科学版),2008, 27(3): 91-95. Solutions to a Critical Elliptic System Involving Negative Exponents KangDongsheng1,XuLiangshun1,CaoYuping2 (1 College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China;2 Library, South-Central University for Nationalities, Wuhan 430074, China) In this paper, a system of elliptic equations was investigated, which involves strongly-coupled critical nonlinearities and negative-exponent terms. Several constraint sets were defined, the infimums of the energy functional on the constraint sets were studied by complicated analytical techniques, and the explicit expression of a critical constant was obtained. Finally, the existence of positive solutions to the system was verified under certain conditions, and for the first time, the related conclusions for the single critical elliptic equation were extended to the system of critical elliptic equations involving negative-exponent terms. elliptic system; critical nonlinearities; negative-exponent term; variational method 2017-01-11 康东升(1967-),男,教授,博士,研究方向:偏微分方程,E-mail:dongshengkang@scuec.edu.cn 国家自然科学基金资助项目(11601530);中南民族大学研究生科研创新项目(2017sycxjj083) O175.25 A 1672-4321(2017)02-0143-05







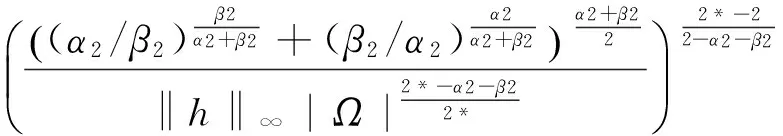
2 定理1的证明