幂级数J-Armendariz环*
2017-06-10任艳丽李敏
任艳丽,李敏
(1. 南京晓庄学院信息工程学院,江苏 南京 211171; 2. 南京信息工程大学数学与统计学院,江苏 南京 210044)
幂级数J-Armendariz环*
任艳丽1,李敏2
(1. 南京晓庄学院信息工程学院,江苏 南京 211171; 2. 南京信息工程大学数学与统计学院,江苏 南京 210044)
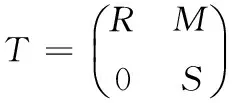
幂级数;幂级数Armendariz环;幂级数J-Armendariz环; 幂级数弱Armendariz环
本文假定所研究的环R都是有单位元1的结合环,α是环R的一个非零自同态。我们分别以R[x]和R[[x]]表示R上的多项式环和R上的幂级数环,分别以nil(R)和J(R)表示环R中所有幂零元的集合和R的Jacobsin根,分别以MN(R),Tn(R),In,Eij表示R上的n阶全矩阵环,n阶上三角矩阵环,n阶单位矩阵和第i行第j列为1其余为0的n阶矩阵。
近年来,关于幂级数环的研究和讨论有很多[1-7]。Kim等在文献[1]中称一个环R为幂级
由f(x)g(x)=0可以推出aibj∈nil(R),对一切i和j。幂级数Armendariz环是幂级数弱Armendariz环,但反之不成立(见文献[2]的Remark6)。
1 定义及例子
下面, 我们将幂级数Armendariz环的概念做另一方面的推广。
定义1 称一个环R是幂级数J-Armendariz环,如果对任意的幂级数
由f(x)g(x)=0可以推出aibj=J(R),对任意的i和j。
显然幂级数Armendariz环是幂级数J-Armendariz环。
命题1 幂级数J-Armendariz环的理想子环也是幂级数J-Armendariz环。
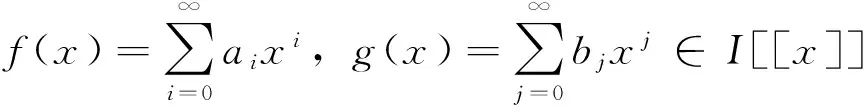
当nil(R)是环R的理想(即R是NI环)时,nil(R)=J(R)(见文献[8]的命题2.7(2)), 幂级数弱Armendariz环是幂级数J-Armendariz环。下面的例子说明,幂级数J-Armendariz环未必是幂级数弱Armendariz环。
例1 设F=Z2,A是幂级数环F[[t]]上的三阶全矩阵环,
B={M=(mij)∈A|mij∈tF[[t]],其中i=3或j=3时,mij=0},

且满足f(x)g(x)=0,则
因此环R是幂级数J-Armendariz环。 但对于环R上的两个多项式,有f(x)g(x)=0, 而te11t(e21+e22)∉nil(R),因此环R不是幂级数弱Armendariz环。
这样我们就知道,幂级数Armendariz环⟹幂级数弱Armendariz环;幂级数Armendariz环⟹幂级数J-Armendariz环,但反之都不成立。对于NI环,有幂级数弱Armendariz环⟹幂级数J-Armendariz环。
2 幂级数J-Armendariz环的扩张
给定两个环R,S和一个双模RMS, 令

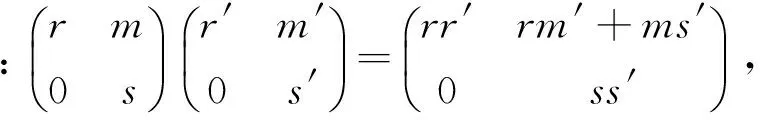
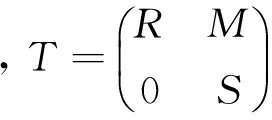
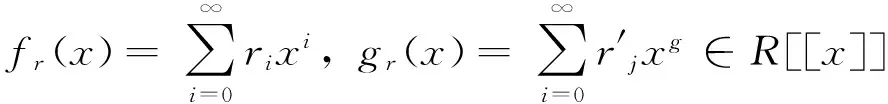
于是由f(x)g(x)=0知fr(x)gr(x)=0,fs(x)gs(x)=0。因为R,S是幂级数J-Armendariz环,所以
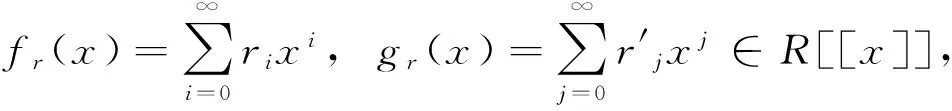
满足fs(x)gs(x)=0。现在令
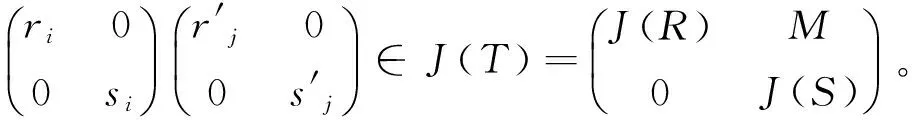
这推出R,S都是幂级数J-Armendariz环。
推论1 设Tn(R)是n阶上三角矩阵环, 则Tn(R)是幂级数J-Armendariz环当且仅当R是幂级数J-Armendariz环。
据命题2,自然问:环R上的n阶全矩阵环Mn(R)是否也是幂级数J-Armendariz环, 其中n≥2。下面的例子给出了否定回答。
例2 设F是一个域且R=M2(F)。取
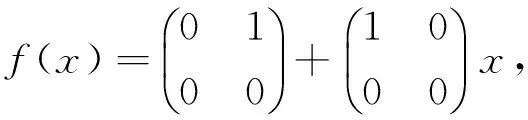

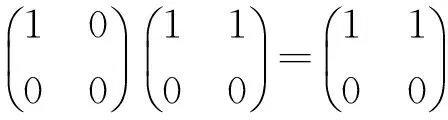
命题3 设R是一个环,I是环R的一个理想且I⊆J(R)。如果R/I是幂级数J-Armendariz环,则R是幂级数J-Armendariz环。
证明 设

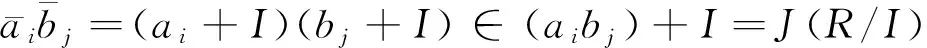
称一个环R为局部环,如果R/J(R)是除环。
推论2 如果R是一个局部环,则环R是幂级数J-Armendariz环。
证明 因为R是局部环,R/J(R)是除环,而已知约化环是幂级数Armendariz环,所以R/J(R)是幂级数J-Armendariz环。由命题3 知结论成立。
但是,当R是一个局部环时,R未必是幂级数弱Armendariz环。
例 3[3]设F是一个域,R=M2(F)且R1=R[[t]]。
其中I是F的单位矩阵。 显然S是局部环, 由推论2知,环S是幂级数J-Armendariz环。 但是取
f(x)=e11t+e12tx,g(x)=e21t+e11tx∈S[x]有f(x)g(x)=0,由于(e11t)2∉nil(S),故环R不是幂级数弱Armendariz环。
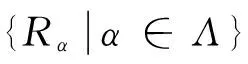
证明 必要性。设
fα(x)=a0α+a1αx+…+apαxp+…,
gα(x)=b0α+b1αx+…+bqαxq+…
满足fα(x)gα(x)=0。取
其中
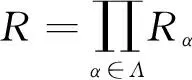
充分性。设每一个Rα是幂级数J-Armendariz环,
且满足f(x)g(x)=0, 其中ai=(aiα)α∈Λ,bj=(bjα)α∈Λ∈R,i,j≥0。对任意的α∈Λ, 取
fα(x)=a0a+a1αx+…+apαxp+…,
gα(x)=b0a+b1αx+…+bqαxq+…

推论3
(i) 环直和R=⊕α∈ΩRα是幂级数J-Armendariz环当且仅当每一个Rα是幂级数J-Armendariz环;
(ii) 设R是一个环,e∈R是中心幂等元,则R是幂级数J-Armendariz环当且仅当eR和(1-e)R都是幂级数J-Armendariz环。
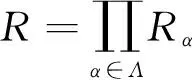
(ii) 因为e∈R是中心幂等元,eR和(1-e)R都是R的理想, 由R=eR⊕(1-e)R以及情形(i)即知。
称一个环R是Abel环,如果环R中每一个幂等元都是中心的。 由文献 [10]的定理3.6知,幂级数Armendariz环是Abel环。下面的例子说明幂级数J-Armendariz环未必是Abel环。

命题 4 设R是幂级数J-Armendariz环,e∈R是任意幂等元, 则eRe是幂级数J-Armendariz环。

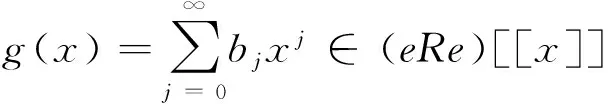
且满足f(x)g(x)=0。因为环R是幂级数J-Armendariz环,所以aibi∈J(R),对任意的i,j。又因为aibi∈eRe,所以aibi∈J(R)∩eRe=J(eRe)。因此环eRe是幂级数J-Armendariz环。
定理2 如果环R是幂级数J-Armendariz环,满足J(R)[x]=J(R[x]), 则R[x]是幂级数J-Armendariz环。
证明 设
并且F(y)G(y)=0, 其中
取kn=degf0+degf1+…+degfn+degg0+degg1+…+deggn+1,并且yn=xkn,其中deg (f)表示多项式f的次数。于是有
U(x)=f0+f1xk1+f2xk2+…+
fnxkn+…∈R[[x]],
V(x)=g0+g1xk1+g2xk2+…+
gnxkn+…∈R[[x]]
即
U(x) =a00+a01x+a02x2+ … +a0txt+
a10xk1+a11xk1 + 1+a12xk1 + 2+ … +
a1txk1 + t+ … +
an0xkn+an1xkn + 1+an2xkn + 2+ … +
antxkn + t+…∈R[[x]],
V(x)=b00+b01x+b02x2+…+b0hxh+
b10xk1+b11xk1+1+b12xk1+2+…+b1hxk1+h+…+
bnoxkn+bn1xkn+1+bn2xkn+2+…+
bnhxkn+h+…∈R[[x]]
由kn的取法知,这样构造的U(x)是包含所有fi系数的幂级数,V(x)是包含所有gj系数的幂级数。由F(y)G(y)=0得U(x)V(x)=0。因为环R是幂级数J-Armendariz环,所以有aisbjl∈J(R),对任意的i,s,j,l。于是有fi(x)gj(x)∈J(R)[x],对任意的i,j。已知J(R[x])=J(R)[x],从而有fi(x)gj(x)∈J(R[x]),对任意的i,j。因此知R[x]是幂级数J-Armendariz环。
称环R的一个元素μ是右正则的,如果对任意的r∈R,由μr=0可以推出r=0。类似地,可定义左正则元。如果μ既是左正则元又是右正则元,则称μ是正则元。
定理3 设Δ是有限环R中的由中心正则元构成的乘法封闭子集,如果R是幂级数J-Armendariz环,则Δ-1R是幂级数J-Armendariz环。
证明 因为R是有限环,Δ是一个左Ore集合, 所以对任何F(x),G(x)∈(Δ-1R)[[x]],有
其中u,v是中心正则元,ai,bj∈R,对任意的i,j。如果F(x)G(x)=0,取
则由
0=F(x)G(x)=
(uv)-kf(x)g(x)
得到f(x)g(x)=0。因为R是幂级数J-Armendariz环, 所以有aibj∈J(R), 对任意的i,j,从而有αiβj=(uv)-1aibj∈J(Δ-1R)。因此Δ-1R是幂级数J-Armendariz环。
推论4 如果环R是有限环,则R[x]是幂级数J-Armendariz环当且仅当R[x:x-1]是幂级数J-Armendariz环。
证明 令Δ={1,x,x2,…},则Δ是环R[x]中的乘法封闭左Ore子集。因为R[x:x-1]=Δ-1R[x],所以根据定理3知结论成立。
[1]KIMNK,LEEKH,LEEY.Powerseriesringssatisfyingazerodivisorproperty[J].CommAlgebra, 2006, 34(6): 2205-2218.
[2]HIZEMS.AnoteonnilpowerserieswiseArmendarizrings[J].RendCircMatPalermo, 2010, 59(1): 87-99.
[3]HUHC,KIMCO,KIMEJ,etal.Nilradicalsofpowerseriesringsandnilpowerseriesrings[J].JKoreanMathSoc, 2005, 42(5): 1003-1015.
[4]HUHC,KIMHK,LEEDS,etal.Primeradicalsofformalpowerseriesrings[J].BullKoreanMathSoc, 2001, 38(4): 623-633.
[5]NASR-ISFAHANIA,MOUSSAVIA.OnskewpowerserieswiseArmendarizrings[J].CommAlgebra, 2011, 39(9): 3114-3132.
[6]HONGCY,KIMNK,KWAKTK.Nilradicalsofskewpowerseriesrings[J].BullKoreanMathSoc, 2004, 41(3): 507-519.
[7] 普昭年. 斜π-Armendariz环[J]. 中山大学学报(自然科学版),2012, 51(3): 39-43.PUZN.Onskewπ-Armendarizrings[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2012, 51(3): 39-43.
[8]HWANGSU,JEONYC,LEEY.StructureandtopologicalofNIrings[J].JAlgebra, 2006, 302(1): 186-199.
[9] 王尧, 任艳丽.MoritaContext环的根[J]. 数学进展, 2016, 45(2): 195-205.WANGY,RENYL.RadicalsofMoritaContextrings[J].AdvancesinMathematics(China), 2016, 45(2): 195-205.
[10]KWAKTK,LEEY.Onnilpotentpowerserieswithnilpotentcoefficients[J].KoreanJMath, 2013, 21(1): 41-53.
Power series J-Armendariz rings
RENYanli1,LIMin2
(1. School of Information Engineering, Nanjing Xiaozhuang University, Nanjing 211171, China; 2. School of Mathematics and Statistics, Nanjing University of Information Science and Technology, Nanjing 210044, China)
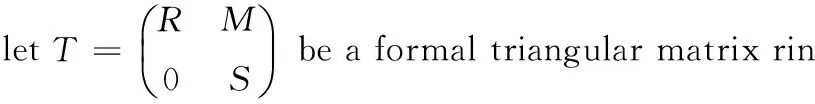
power series; power series Armendariz ring; power series J-Armendariz ring; weak power series Armendariz ring
2016-08-25 基金项目:国家自然科学基金 (11101217);江苏省自然科学基金 (BK20141476)
任艳丽(1965年生),女;研究方向:结合环、结合代数;E-mail: renyanlisx@163.com
10.13471/j.cnki.acta.snus.2017.02.008
O
A
0529-6579(2017)02-0048-05
