张隽,曹重光

(黑龙江大学数学科学学院,黑龙江 哈尔滨 150080)

关于上三角矩阵代数之间经典伴随交换单射

张隽,曹重光

(黑龙江大学数学科学学院,黑龙江 哈尔滨 150080)

令F是一个域,且|F|＞n+1,m,n为整数且m,n≥3.Tn(Tm)(F)是F上所有n×n(m×m)上三角矩阵的集合.本文中,刻画了从Tn(F)到Tm(F)的保经典伴随交换的单映射,给出了映射的表达式,对相应的方阵的工作是一个新的补充,所用方法是将其化归为相应的线性保持问题.

域;保伴随交换;单映射

1 引言

刻画矩阵集合保持某些性质的映射称为矩阵保持问题研究.近年来,这种研究更感兴趣于映射没有线性和加法假定的情形,例如文献[1],[5].本文考虑上三角矩阵代数类似文献[5]的问题.

设F是一个域,Tn(Tm)(F)是F上所有n×n(m×m)上三角矩阵的集合..设φ是Tn(F)到Tm(F)的映射.如果定义

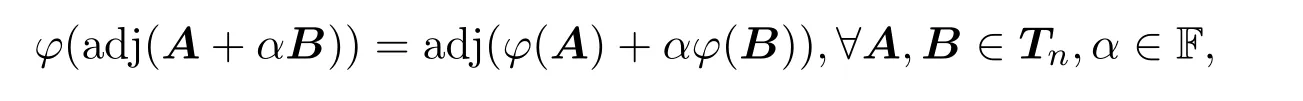
则称φ是一个经典伴随交换映射,又称φ满足条件(Ac−1).

本文目的是刻画域上上三角矩阵经典伴随交换单射.在本文中记I为单位矩阵,用0记零元,用O记零矩阵,用F∗记F中所有非0元的集合,Eij(i,j)位置是1,其余位置是零的矩阵.记[1,n]={1,2,···,n}.

引理 1.1设F为一个域,|F|＞n+1,n为整数且n≥3,令A,B∈Tn,那么

(a)存在一个矩阵X∈Tn,使得rank(A+X)=rank(B+X)=n.

(b)存在一个非O的矩阵X∈Tn,A是可逆的或者X是可逆的,但不能两者都可逆,使得rank(A+X)=n.

(c)若rank(A+B)=n,则存在一个标量λ0∈F且λ01,使得rank(A+λ0B)=n.

证明首先，对A∈Tn作如下定义:

其中,A=aij,i,j∈[1,n].

则rank(B+X)=n.若想推出rank(A+X)=n,只需令

秩为n,即令p+ci0,i∈[1,n].故令p0,p−c1,···,p−cn,由|F|＞n+1,可推出存在X=pI−B使得rank(A+X)=rank(B+X)=n.

(b)若A是可逆的,令X=AE12,结论显然成立.若A是奇异的,令X=cI−A,注意到,若想推出X是可逆的,只需令

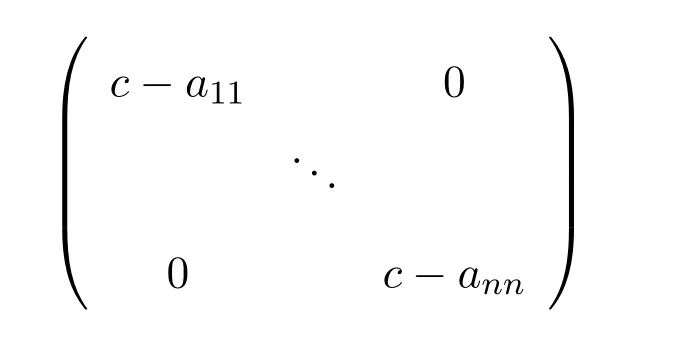
秩为n,即令c−aii0,i∈[1,n],若想推出rank(A+X)=n,只需令

(c)令λ∈F且p(λ)=det(A+λB).由p(1)0,知p是一个非0多项式.若B=O,那么rankA=n,结论成立.若BO注意到,

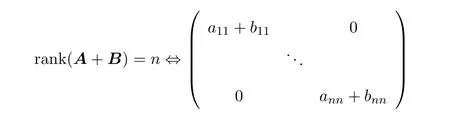
秩为n⇔aii+bii0,i∈[1,n],

秩为n⇔aii+λ0bii0,i∈[1,n].显然bii不全为0.不妨设

若bll=0,则all0,故all+λ0bll0,若bjj0,则对于由|F|＞n+1,可推出存在一个标量λ0使得rank(A+λ0B)=n.

引理1.2设F为一个域,m,n为整数且m,n≥3,令A∈Tn,若φ:Tn→Tm为一个单射满足(Ac−1),那么rankφ(A)=m当且仅当rankA=n.

证明必要性：假设rankA≤n−1,则adj(adjA)=O,由φ是单射,有φ(adj(adjA))=O,由φ满足(Ac−1)得adj(adj(φ(A)))=O.注意到rank(φ(A))=m,则

矛盾,故

充分性:假设rankφ(A)≤m−1,则adj(adj(φ(A)))=O,由φ满足(Ac−1)得φ(adj(adjA)) =O,由φ是单射,可得adj(adjA)=O.另一方面,由rankA=n,可得(adj(adjA))=n,推出矛盾,故rankφ(A)=m.

推论1设F为一个域,m,n为整数,m,n≥3,令A,B∈Tn,若φ:Tn→Tm为一个单射满足(Ac−1),α∈F,那么rank(A+αB)=n当且仅当rank(φ(A)+αφ(B))=m.

证明由引理1.2得,

rank(A+αB)=n⇔rank(adj(A+αB))=n⇔rankφ(adj(A+αB))=m

⇔rank(adj(φ(A)+αφ(B)))=m⇔rank(φ(A)+αφ(B))=m.

引理 1.3令F为一个域,|F|＞n+1,m,n是整数,且m,n≥3.若φ:Tn→Tm一个映射满足(Ac−1)且φ是单射,那么φ是线性的.

证明令A,B∈Tn,α∈F,由引理1.1可得rank(A+αB)=n,由引理(1.2)和推论1知φ(A+αB)和φ(A)+αφ(B)是秩m,那么,

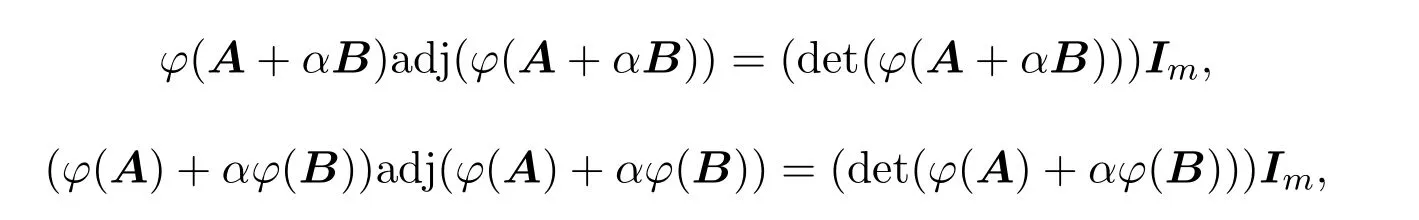
由adj(φ(A)+αφ(B))=adj(φ(A+αB))得到,

即

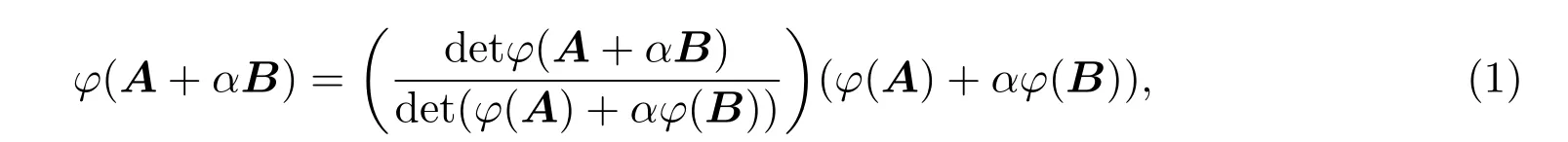
类似可证

若在(1)中取A=O,αB是秩n,则有

下面分6部分进行证明.

(a)要证对于每个非0标量µ∈F,X∈Tn,rankX=n,有

由引理(1.1)(b)知存在一个非O的奇异矩阵Y∈Tn使rank(µX+Y)=n.由引理1.2和推论1,注意到φ(µX+Y),µφ(X)+φ(Y),φ(µX)+φ(Y)是秩m.由(1),(2)可得

因此

令a1=det(µφ(X)+φ(Y),a2=det(φ(µX)+φ(Y)),由(5)可得

假设a1a2,且rankX=n,由(3)知φ(µX)和φ(X)是线性相关的,因此φ(µX)=λφ(X), λ∈F,将其代入(6)中得到

由 φ是单射且易证 φ(O)=O可知φ(X)和φ(Y)非O,得到φ(X),φ(Y)是线性相关的且rank φ(X)=rankφ(Y).另一方面,由引理1.2,注意到φ(X)是可逆的,φ(Y)是奇异的,因此,rank φ(X)rankφ(Y),矛盾.显然,可得到det(µφ(X)+φ(Y))=det(φ(µX)+φ(Y)),因此(4)成立.

(b)下面证明(7),即若X,Y∈Tn,rank(X+Y)=n,X,Y是线性无关的,那么φ(X), φ(Y)是线性无关的.假设φ(X),φ(Y)是线性相关的,那么存在一个标量γ∈F使φ(Y)= γφ(X).由rank(X+Y)=n和推论1可得rank(φ(X)+φ(Y))=m,则rankφ(X)=m.由引理 1.2得到 rankX=n,因此由 (4)可得 φ(Y)=γφ(X)=φ(γX),由 φ是单射,得到Y=γX,这说明X,Y是线性相关的,与已知矛盾,那么(7)被证明.

(c)下证(8),即若X,Y∈Tn,有0＜rankX＜n,rankY=n,rank(X+Y)=n,那么

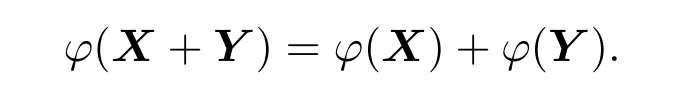
在(1)中取α=1,得到

由|F|＞n+1和引理1.1(c)可知存在一个非0标量α0∈F使rank(X+(1+α0)Y)=n,由(9)可得

由rankX＜n,得到1+α00且rank((1+α0)Y)=rank(α0(Y))=n,因此由(4)有φ(Y +α0(Y))=φ(Y)+φ(α0Y),则得

令b1=det(φ(X+Y)+φ(α0Y)),b2=det(φ(X)+φ(Y+α0Y)),显然,b1,b20.由(9),注意到φ(X+Y),φ(X)+φ(Y)是线性相关的.那么存在一个标量c1∈F使φ(X)+φ(Y)= c1φ(X+Y),由(10)得到

由X,Y线性无关,得到X+Y,α0Y线性相关.进一步,由rank((X+Y)+α0Y)=n和(7)得到φ(X+Y),φ(α0Y)是线性无关.由(11)可得b1=b2,因此,得到φ(X+Y)=φ(X)+φ(Y),因此(8)已被证明.

(d)下面证明 (12),即 φ的齐次性,φ(αA)=αφ(A),对于每个 A∈Tn,α∈F.当α= 0,A=O或rankA=n时,(12)成立.当α0,A是一个非O的奇异矩阵.由引理1.1(b),知存在一个可逆矩阵Z∈Tn使rank(αA+Z)=n,因此rank(A+α−1Z)=n.由(4),(8)得,φ(α(A+α−1Z))=αφ(A+α−1Z)=α(φ(A)+φ(α−1Z))=αφ(A)+αφ(α−1Z)=α(φA))+ φ(Z).另一方面,由(8)可得φ(α(A+α−1Z))=φ(αA+Z)=φ(αA)+φ(Z),因此φ(αA)= αφ(A).因此(12)已被证明.

(e)下面证明(13),即φ(X+Y)=φ(X)+φ(Y),对于每一个矩阵X,Y∈T(n),rank (X+Y)=n.下面分两种情况讨论.若X,Y是线性相关的,由rank(X+Y)=n,假设X0,那么 Y=βX,β∈F.由 φ的齐次性,知 φ(X+Y)=φ((1+β)X)=(1+β)φ(X)= φ(X)+βφ(X)=φ(X)+φ(Y).现在考虑X,Y是线性无关的.由引理1.1(c),知存在一个非0标量β0∈F使得rank(X+(1+β0Y))=n.由(9)和φ的齐次性,得到

由X线性无关和(7)可得φ(X+Y),φ(β0Y)是线性无关的.由类似(11)的证明可得到det (φ(X+Y)+φ(β0Y))=det(φ(X)+φ(Y+β0Y)),因此(13)已被证明.

(f)最后证明(15),即φ是保加法的.令A,B∈Tn,由引理1.1(a)知存在一个矩阵Z∈Tn使得rank(A+Z)=rank(A+B+Z)=n.由(13)注意到φ(A+B+Z)=φ(A+B)+φ(Z).另一方面,由(13)得φ(A+B+Z)=φ(A+Z)+φ(B),由rank(A+Z)=n和(13)得到φ(A+Z)=φ(A)+φ(Z).显然可得,

因此φ(A+B)=φ(A)+φ(B),A,B∈Tn.因此φ是保加法的.综上所诉,由φ的齐次性和φ是保加法的,可得φ是线性的.

引理 1.4[6]令F为一个域,m,n是整数,且m,n≥3.若φ:Tn→Tm一个非零可加保伴随映射满足φ(E1n)0当且仅当存在一个标量一个可逆矩阵P∈Tn和一个域F上的单自同态δ使得

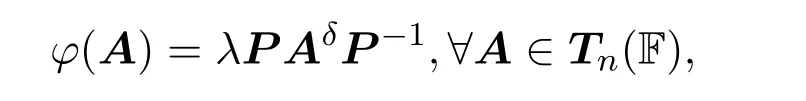
或者

2 主要结果

定理2.1令F为一个域,|F|＞n+1,m,n是整数,且m,n≥3.若φ:Tn→Tm一个单射满足(Ac−1)当且仅当m=n,存在一个可逆矩阵P∈Tn,一个标量λ∈F∗,λn−2=1,一个域F上的单自同态δ,

使得

或者

证明由引理1.3和引理1.4,易证定理2.1.

3 结论

本文给出了在域条件|F|＞n+1下从Tn(F)到Tm(F)的保经典伴随交换的单映射的表达式,对文献[5]的关于方阵的结果是一个重要补充,其创新点在于通过一系列步骤证明了映射是线性的,对同类工作有一定启发意义.

[1]Li C K,Plevnik L,emrl P.Preservers of matrix pairs with a fixed inner product value[J].Operators and matrices,2012,6(3):433-464.

[2]Cao C G,Ge Y L,Yao H M.Maps preserving classical adjoint of products of two matrices[J].Linear and Multilinear Algebra,2013,61(12):1593-1604.

[3]Huang L P.Geometry of Matrices over Ring[M].Beijing:Science Press,2006.

[4]You H,Wang Z Y.K-Potence preserving maps without the Linearty and surjectivity assumptions[J].Linear Algebra Appl.,2007,426:238-254.

[5]Wai leong Chooi,Wei Shean Ng.On classical adjoint-commuting mappings between matrix algebras[J]. Linear Algebra Appl.,2010,432:2589-2599.

[6]Zhang X,Tang X M,Cao C G.Preserver Problems on Spaces of Matrices[M].Beijing:Science Press,2007.

On classical adjoint-commuting injective mappings between upper triangular matrix algebras

Zhang Jun,Cao chongguang
(School of Mathematical Science,Heilongjiang University,Harbin 150080,China)

Let F be a field and let m and n be integers with m,n≥3,Tn(Tm)(F)be the set of all n×n(m×m) upper triangular matrices over F.This paper describes a induced map preserving classical adjoint-commuting injective mappings from Tn(F)to Tm(F),gives expressions of the map,adds the work of relevant square matrix. This paper use ways of translating the problem into relevant linear preserving problems.

field,preserving multiplicative,injective map

O178

A

1008-5513(2017)02-0204-07

10.3969/j.issn.1008-5513.2017.02.012

2016-10-10.

国家自然科学基金(11371109).

张隽(1991-),硕士生,研究方向：矩阵代数.

2010 MSC:15A04