何家莉

(玉林师范学院数学与统计学院,广西 玉林 537000)

软拓扑空间的分离性质

何家莉

(玉林师范学院数学与统计学院,广西 玉林 537000)

研究了软拓扑空间的相关性质.采用经典拓扑学的定义方法,定义了新的软点和软连续,证明了软拓扑空间及乘积拓扑空间有关的分离性质,通过例子说明了各种分离性质之间的关系,进一步推广了软拓扑空间.

软点;软分离性质;乘积空间;软集

1 引言

近年来在各个领域中出现了大量的不确定信息.为了解决这些不确定性,文献[1]引入模糊集理论.文献[2]介绍了粗糙集理论,文献[3]介绍了区间数学理论.尽管这些理论已经应用在模式识别,数据挖掘和机器学习等方面,但它们仍然有自己的缺陷.为了解决这些缺陷,文献[4]引入了软集的概念并在文献[5]中介绍了软集的应用背景.随后,文献[6]引入了软集中参数约减概念.文献[7]引入了软集数据分析方法.文献[8]证明了软集理论可以构成一个特殊的信息系统.除此之外,许多学者还致力于软群,软半群,软半环[9-11]和软理想[12]的研究.

拓扑结构是重要的数学结构,它在数学中起着极其重要的作用.文献[13]第一次把拓扑结构应用于模糊集.随后,文献[14]把拓扑结构用于粗糙集理论.文献[15]首次提出了基于固定参数的论域的软拓扑空间.文献[16]在软拓扑空间中引入了一些新的概念并讨论了该软拓扑空间新的性质.

众所周知,点在经典的拓扑空间中起到至关重要的作用.如何定义软点吸引着众多学者的研究.文献[16-17]中,分别定义了软点,但他们的定义并不是传统定义的推广.因此本文给出了软点的新定义并讨论了该定义与以前所给定义之间的关系.除此之外,在软拓扑空间中还得到了关于软点的特殊性质.接着讨论软拓扑空间及乘积空间的分离性质并给出例子说明分离性之间的关系.

2 预备知识

文献[4]用如下方法定义了软集.U是论域,E是参数集.P(U)表示U的幂集,令A,B⊆E.

定义2.1[4](F,A)称为论域U上的软集,若F是从A→P(U)的映射;论域U上的全体软集构成的集簇记为SSE(U).

定义 2.2[5](F,A)和(G,B)是论域U上两个软集,若A⊆B且对于任意e∈A,有 F(e)⊆G(e),则(F,A)称为(G,B)的软子集.记作

定义 2.3[5]在论域U上,若(F,A)是(G,B)的软子集且(G,B)是(F,A)软子集,则称(F,A)和(G,B)为软等价.

定义 2.4[18]软集(F,A)的补集定义为(F,A)c=(Fc,A),其中Fc是由A到P(U)的映射且对于任意的a∈A有Fc(a)=U−F(a).

注记 2.1Fc称为函数F的软补集.显然(Fc)c=F,((F,A)c)c=(F,A).

定义2.5[3]论域U上的软集(F,A)称为空软集,如果对任意e∈A有F(e)=ϕ,记作ΦA;软集(F,A)称为全软集,如果对任意e∈A有F(e)=U,记作UA.显然

定义2.6[4]论域U上,软集(H,C)称为软集(F,A)和(G,B)的并,其中C=A∪B且对于任意e∈A满足

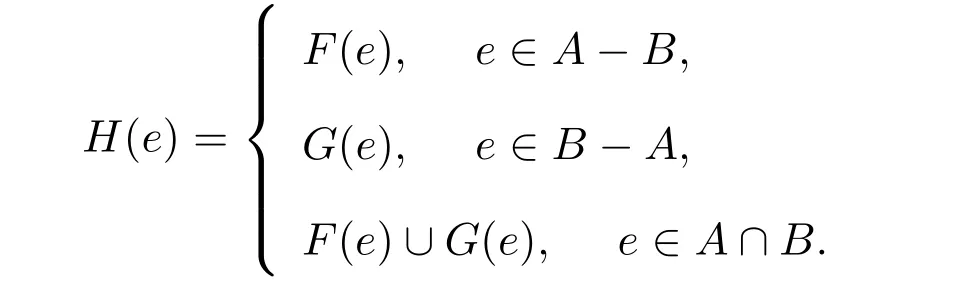
定义2.7[4]论域U上,软集(H,C)称为软集(F,A)和(G,B)的交,其中C=A∩B且对所有e∈C满足H(e)=F(e)∩G(e).记作:

定义 2.8[16]软集(F,E)∈SSE(U)称作论域U上的软点,如果对存在e∈E有F(e)ϕ且对所有e′∈(E−{e})有F(e′)=ϕ.记作:eF.

定义 2.9[19]软集(F,A)称为论域U上的软点,如果存在x0∈U 及A⊆E,对任意的e∈A有FA(e)={x0}且对任意的e′∈E−A,有FA(e′)=ϕ.记作:

定义 2.10[19]称软点eF在软集(G,A)内,如果e∈A且F(e)⊆G(e).记作

定义2.11[19](两软集的笛卡尔乘积),的笛卡尔乘积定义为(F×G,A×B),其中对于任意(e,k)∈A×B,A⊂E1,B⊂E2有(F×G,A×B)(e,k)=FA(e)×GB(k).

定义 2.12[19]软集(pq)i,i∈{1,2}映射称为从U1×U2到Ui的软投射,如果

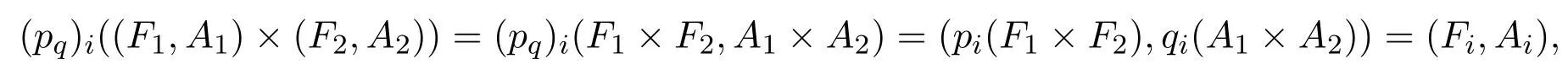
定义 2.13[19](U,τ,E)是软拓扑空间.τ的子集B是的τ基,在τ中的每个元素都可以表示为B中一些成员的并.

定义 2.14[19](U,τ,E)是软拓扑空间.τ的子集S是的τ子基,在S中有限交构成的簇是τ的基.

定义 2.15[19]{(Ui,τi,Ei):i∈I}是软拓扑空间簇.由{(pq)i:i∈I}簇在上生成的软拓扑称为在U上的乘积软拓扑.((Pq)i是从U到Ui,i∈I的投影映射).

引理 2.1[19]软投影映射

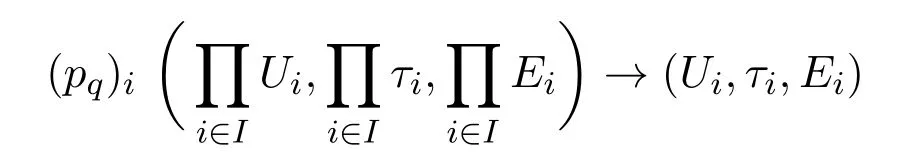
是开映射.

定义 2.16(U,τ,E)是软拓扑空间.软集称为一个软点,如存在a0∈E及x0∈U使得F(a0)={x0}及对任意a∈E−{a0}有F(a)=ϕ,记作中的所有软点用SP(SSE(U))表示.

注记 2.2把软包含关系作为序关系.是布尔格.所有这些定义的软点称为原子.如果把软拓扑空间看成是模糊空间,则所有这些软点都是模糊点.

性质 2.1是两个软集,且如果

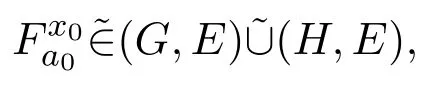
证明令如果则对任意e∈E,有K(e)=H(e)∪G(e).因为a0∈E,由定义2.16,有x0∈H(a0)∪G(a0).因此x0∈H(a0)或者x0∈G(a0),所以或者

3 软拓扑空间的分离性质

在任何空间中,点都起着重要作用.在软拓扑空间上定义了软点.接下来探讨软拓扑空间和乘积软拓扑空间的分离性质.在这一节,假设在相同的软拓扑空间中参数都是相同的.

定义 3.1[20]τ是论域U上带有固定的参数集E的软集簇,则τ⊆SSE(U)称为U上的软拓扑,如果

(1)ΦE,UE属于τ;

(2)在τ中的任意软集的并仍属于τ;

(3)在τ中任意两个软集的交仍属于τ.

定义3.2(U,τ,E)是软拓扑空间,软集(G,E)称为软点的软邻域,如果存在一个软开集(H,E)使得如果则(G,E)称为软开邻域.

定义 3.3[16](U,τ,E)是软拓扑空间,(G,E)是U上的软集.(G,E)的软闭包是软集是软闭集且

性质 3.1(U,τ,E)是软拓扑空间,则(G,E)是软开集当且仅当对于每个包含于(G,E)的软点,(G,E)是该软点的软邻域.

证明(⇒)令是任意包含于(G,E)的软点,因为(G,E)是软开集,则

定理3.1B是一个软点的软邻域系,则B中有限成员的交仍属于B,且每一个包含B中成员的软集都属于B.

证明令 (R,E)和 (S,E)都是软点的软邻域.由定义 3.2,存在有软开集 (F,E)和(G,E)使得则是软开集并且

所以B的有限成员的交仍属于B.综上所述,容易验证每一个包含B成员的软集都属于B.

定义 3.4(U,τ,E)是软拓扑空间,对于任意如果存在软集(H,E),(G,E)满足时,则称(U,τ,E)为软T0空间.

例3.1令U={u1,u2},E={e1,e2}且满足F1(e1)={u1},F1(e2)=ϕ,F2(e1)=ϕ,F2(e2)={u2},F3(e1)={u1},F3(e2)={u2}.由定义3.4,很容易证明(U,τ,E)不是软T0空间.

例3.2令U={u1,u2},E={e1,e2}且

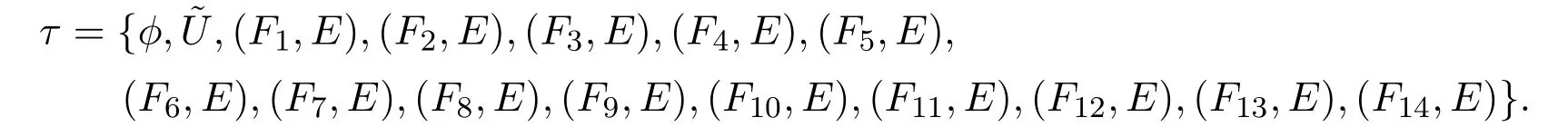
满足

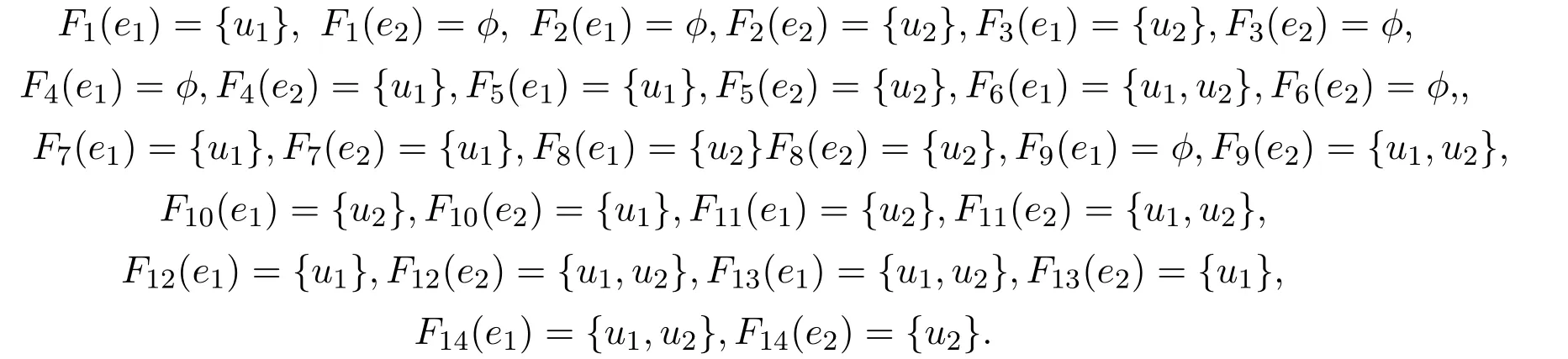
由此,可知(U,τ,E)是软T0空间.

定理 3.2(U,τ,E)是软拓扑空间,则以下条件是等价的:

(1)(U,τ,E)是软T0空间.

证明(1)⇒(2)假设的任意邻域包含并且的任意邻域包含这与 (1)矛盾.(2)⇒(1)显然可证.(2)⇒(3)显然可证.(3)⇒(2)假设且很容易可证实这与(3)矛盾的.

定理 3.3{(Ui,τi,Ei):i∈I}是软拓扑空间簇,则是软T0空间当且仅当如果对于任意i∈I有(Ui,τi,Ei)是软T0空间.

证明(⇒)令

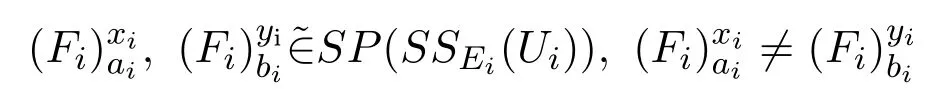
对于每个i∈I,

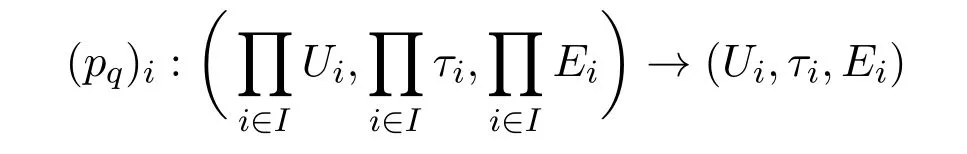
是软投影映射.存在有

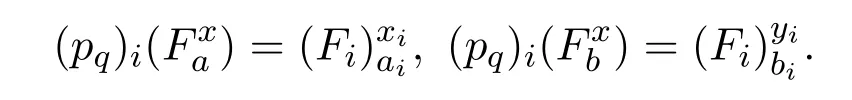
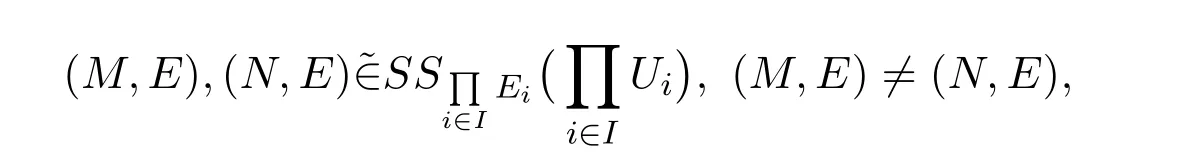
然后有

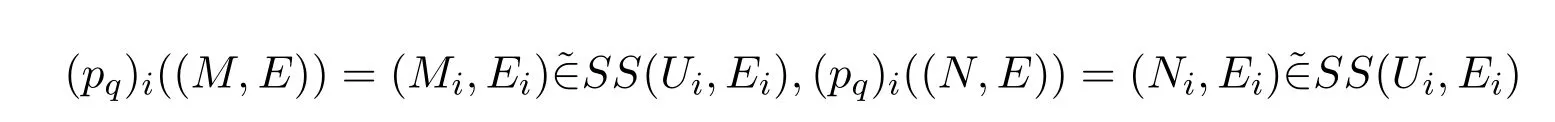
所以(Ui,τi,Ei)是对每个i∈I的软T0空间.

(⇐)对于每个

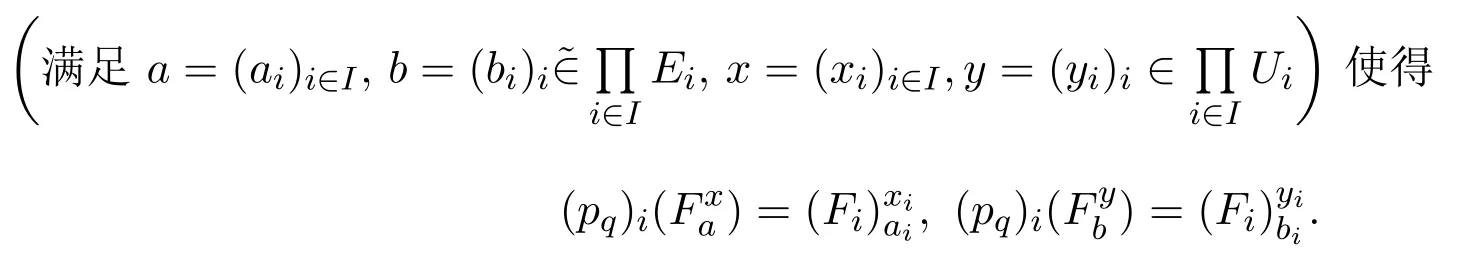
因为对于任意的i∈I,(Ui,τi,Ei)是软T0空间,那么存在有使得且或者且因此有且或者

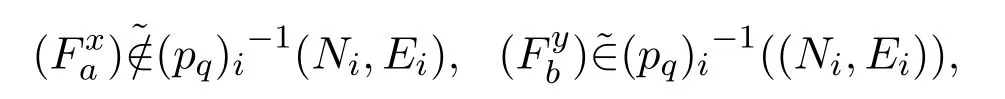
定义 3.5(U,τ,E)是软拓扑空间,对于任意且如果存在软集(H,E)和(G,E)使得且则(U,τ,E)称为软T1空间.

性质 3.2软T1空间⇒软T0空间

证明从以上定义,显然可证.

例 3.3很容易检验例3.2就是软T1空间.

例3.4令U={u1,u2},E={e1,e2}且

满足

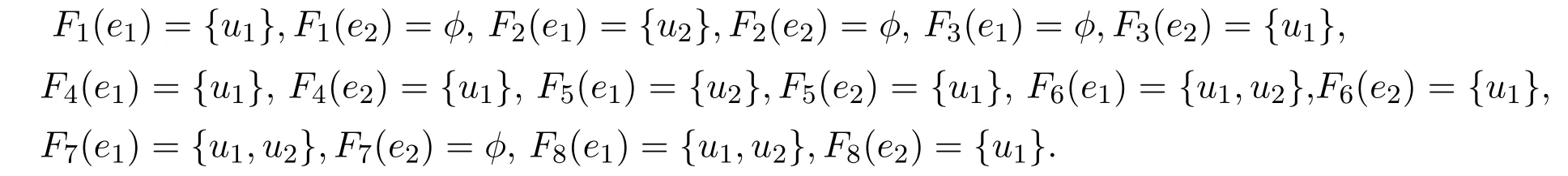
通过以上定义,很容易检验(U,τ,E)不是软T1空间.

定理 3.4(U,τ,E)是软拓扑空间,则以下结论等价:

(1)(U,τ,E)是软T1空间,

(2)每个软单点集是软闭集,

(3)含有有限个元素的软集都是软闭集.

证明(1)⇒(2)对于任意软点由于 (U,τ,E)是软T1空间,对于任意且存在有的软邻域(G,E)使得有=ϕ.因此,有所以每个软单点集都是软闭集.(2)⇒(3)显然易证.(3)⇒(1)假设对任意且因为每个软单点集在τ中都是软闭集,所以都是软开集,有因此(U,τ,E)是软T1空间.

定理 3.5{(Ui,τi,Ei):i∈I}是软拓扑空间簇,则是软T1空间当且仅当对任意i∈I,(Ui,τi,Ei)是软T1空间.

证明该证明与定理3.3类似.

定义 3.6(U,τ,E)是软拓扑空间,对于任意且如果存在软集(H,E)和(G,E)使得且则(U,τ,E)称为软T2空间.

例3.5令U={u1,u2},E={e1,e2}及(F1,E),(F2,E)},满足

F1(e1)={u1},F1(e2)={u2},F2(e1)={u2},F2(e2)={u1},从以上定义,很容易验证(U,τ,E)不是软T2空间.

注记 3.1从例3.2可知,其中的软拓扑空间(U,τ,E)是软T2空间.

性质 3.3软T2空间⇒软T1空间.

证明根据定义,显然成立.

由定理1,可以很容易得到以下结论:

引理 3.1(U,τ,E)是软拓扑空间,是软邻域系,且有以下特征:(BP1)对于每个满足的软点且每个有(BP2)如果则存在有使得(BP3)对于任意存在有使得

定理 3.6设是在论域U上的软集簇,具有性质(BP1)-(BP3).除此之外,如果该软集簇还有以下属性,(BP4)对于每一对不同的软点存在有且使得则由软邻域系统生成的软拓扑空间(U,E)是软T2空间.

证明由于软邻域系统可以生成软拓扑,所以(U,τ,E)是软拓扑空间.由性质(BP4),易证(U,τ,E)是软T2空间.

定理 3.7{(Ui,τi,Ei):i∈I}是软拓扑空间簇,则是软T2空间当且仅当对任意i∈I,(Ui,τi,Ei)是软T2空间.

证明该证明与定理3.3证明类似.

定义3.7[20]SSE(U)和SSL(Y)分别是在U和L上的软集簇.则从SSE(U)到SSL(Y)的映射称为软映射,记作φψ:SSE(U)→SSL(Y).其中φ:U→Y且ψ:E→L是两个映射.

定义 3.8(U1,τ1,E1),(U2,τ2,E2)是两个软拓扑空间,f是(U1,τ1,E1)到(U2,τ2,E2)的软映射,若(U2,τ2,E2)中的每一个软开集(G,E2)的原像f−1((G,E2))是(U1,τ1,E1)中的软开集,则f称为从(U1,τ1,E1)到(U2,τ2,E2)的软连续映射.

定理 3.8对于任意一对从软拓扑空间(U1,τ1,E1)到软T2拓扑空间(U2,τ2,E2)的软连续映射φψ,µν,则软集是(U1,τ1,E1)中的软闭集.

证明将证明软集是软开集.对于任意有因为(U2,τ2,E2)是软T2空间,那么存在软开集(M,E2)和(N,E2)使得且因为φψ,µν是软连续映射,则软集是点的软邻域与

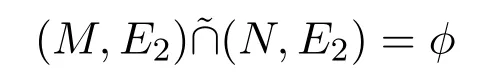
定义 3.9(U,τ,E)是软拓扑空间,是软点,(K,E)是软闭集且如果存在软集(H,E)与(G,E)使得且则(U,τ,E)称为软正则空间.每个T1的正则软拓扑空间(U,τ,E)称为软T3拓扑空间.

例 3.6例3.2也是一个软正则空间.

性质 3.4软T3空间⇒软T2空间.

注记 3.2下面的例子表明了性质3.4的逆命题不成立.

例3.7令U={u1,u2},E={e1,e2}和

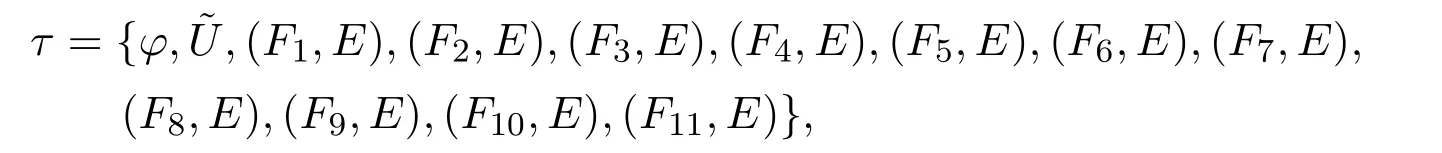
满足

从以上定义,可以很容易证明(U,τ,E)是软T2空间但不是软T3空间.令

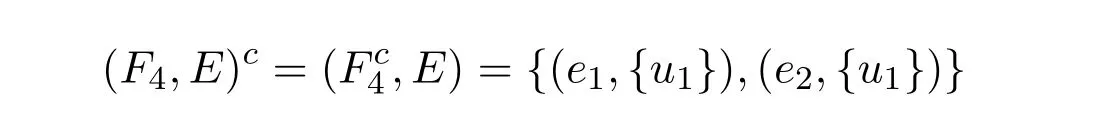
定理 3.9{(Ui,τi,Ei):i∈I}是软拓扑空间簇,则是软T3空间当且仅当(Ui,τi,Ei)对于任意i∈I是软T3空间.

证明该证明与定理3.3类似.

定理 3.10软拓扑空间(U,τ,E)是软正则空间当且仅当对于每个软点和每个包该软点的软开集(G,E),存在一个软开集(H,E)使得

证明(⇒)设则且(G,E)c是软闭集.因为(U,τ,E)是软正则空间,故存在软开集(F,E)和(M,E)使得因此有令(H,E)=(F,E),则(H,E)是软开集且所以存在软开集(H,E)使得

定理 3.11{(Ui,τi,Ei):i∈I}是软拓扑空间簇,则是软正则空间当且仅当对于任意i∈I,(Ui,τi,Ei)是软正则空间.

证明该证明与定理3.3证明类似.

定义 3.10(U,τ,E)是软拓扑空间,(F,E)和(G,E)是两个软闭集且如果存在软集(H,E)和(M,E)使得且则(U,τ,E)称为软正规空间.

如果软T1空间(U,τ,E)是软正规空间,则(U,τ,E)称为软T4空间.

定理 3.12软拓扑空间 (U,τ,E)是软正规空间当且仅当每个软闭集 (F,E)和每个包含(F,E)的软开集(G,E),存在软开集(H,E)使得

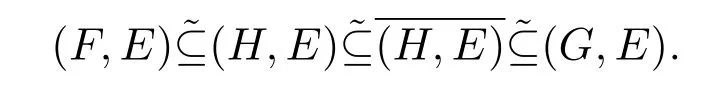
证明该证明与定理3.10证明类似.

性质 3.5软正规空间的乘积空间可以不是软正规空间.

证明一般拓扑中的反例可证.

定理 3.13设X是软拓扑空间,[a,b]是直线R的一个闭区间,则X是软正规空间当且仅当对于X中的任何一个软闭集A和任何一个软连续映射f:A→[a,b]都存在一个软连续映射g:X→[a,b]是f的扩张.

证明由于任何一个闭区间都同胚于[−1,1],不失一般性取[a,b]为[−1,1].

(⇐)设A与B是中的两个不相交的软闭集.定义映射f:A∪B→[−1,1]使得当x∈A时f(x)=−1,当x∈B时f(x)=1.显然f是软连续映射,则映射f有一个软连续扩张.g:X→[−1,1]且满足当时时g(x)=1.进而由于g是软连续映射,因此不难验证X是软正规空间.

(⇒)设X是一个软正规空间,A是X的一个软闭集,f:A→[−1,1]是一个软连续映射.定义对于每一个n≥0,一个软连续映射

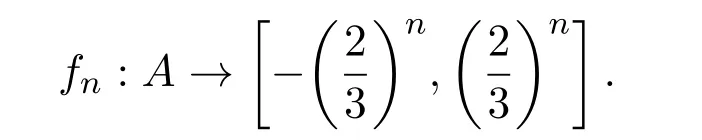
定义对每一个n≥1,一个软连续映射

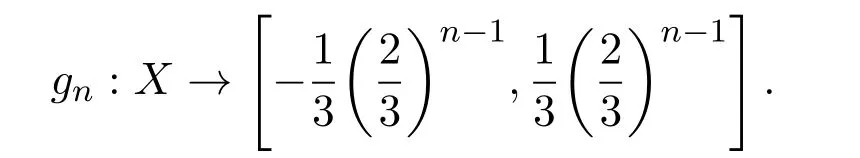
如f0=f:A→[−1,1].对于每一个n＞0.由数学归纳法假设软连续映射fn−1已定义,则∃软连续映射gn使得

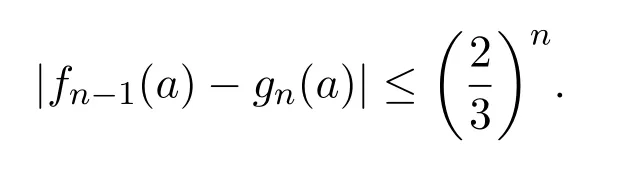
定义fn使得有fn(a)=fn−1(a)−gn(a),则fn是软连续的.定义映射g:X→[−1,1]使得

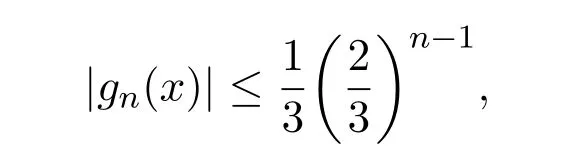
所以

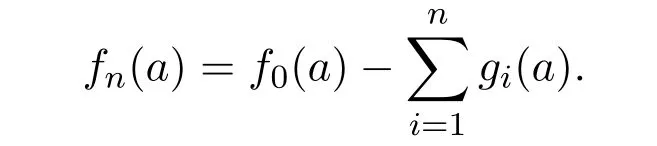
于是

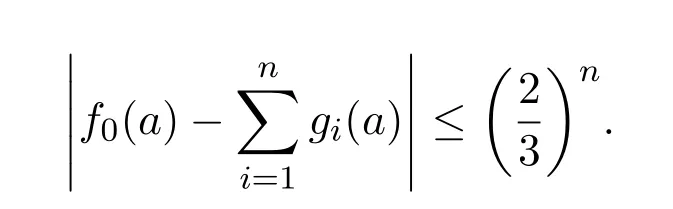
当n→∞时,有g(a)=f0(a)=f(a).因此g是软连续映射f在X上的扩张.

下面证g是软连续映射.

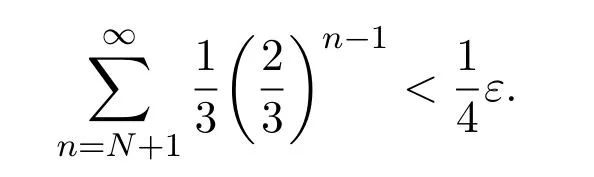
∀n,1≤n≤N,由于gn是软连续,故的一个邻域Un,使得当时,有

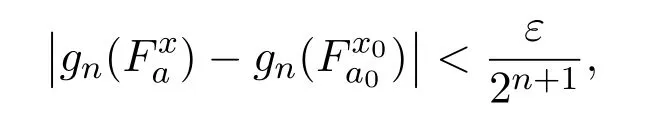
[1]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8:338-353.

[2]Pawlak Z.Rough sets[J].International Journal of Computer Science,1982,11:341-356.

[3]Gorzalzany M B.A method of inference in approximate reasoning based on Interval valued fuzzy sets[J].Fuzzy Sets and Systems,1987,21:1-17.

[4]Molodtsov D.Soft set theory first results[J].Computers and Mathematics with Applications,1999,37:19-31.

[5]Molodtsov D,Leonov V Y,VKovkov D.Soft sets technique and its Applications[J].Nechetkie Sistemy Myagkie Vychisleniya1,2006,14:8-39.

[6]Kong Z,Gao L,Wong L,et al.The normal parameter reduction of soft sets And its algorithm[J].J.Comp.Appl. Math,2008,56:3029-3037.

[7]Zou Yan,Xiao Zhi.Data analysis approaches of soft sets under incomplete information[J].Knowl.Based Syst.,2008,21:941-945.

[8]Pei D,Miao D.From soft sets to information systems[J].In Proceedings of the IEEE International Conference on Granular Computing,2005,2:617-621.

[9]Aktas H,Cagman N.Soft sets and soft groups[J].Information Science,2007,1:2726-2735.

[10]Feng F,Jun Y B,Zhao X.Soft semirings[J].Fuzzy Sets and Systems,2008,56:2621-2628.

[11]Jun Y B,Lee K J.A Khan Soft ordered semigroups[J].Mathematical Logic Quarterly,2010,56:42-50.

[12]Jun Y B,Lee K J,Park C H.Fuzzy soft set theory applied to ideals in d-algebras[J].Computers and Mathematics with Applications,2009,57:367-378.

[13]Chang C L.Fuzzy topological spaces[J].J Math.Anal.Appl,1968,24:182-190.

[14]Lashin E F,Kozae A R,AboKhadra A A.Rough set for topological spaces[J].Internet.J.Approx.Reason,2005,40:35-43.

[15]Muhammad Shabir,MunazzaNaz.On soft topological spaces[J].Computers and Mathematics with Applications,2011,61:1786-1799.

[16]Zorlutuna I,Akdag M,Min W K,Atmaca S.Remarks on soft topological spaces[J].Annals of fuzzy mathematics and informatics,2012,3:171-185.

[17]Abd ü kadir Ayg ü noglu,Halis Ayggn.Some notes on soft topological spaces[J].Neural Computer and Applications,2012,21:S113-S119.

[18]Maji P K,Biswas R,Roy R.Soft set theory[J].Computers and Mathematics with Applications,2003,45:555-562.

[19]IrfanAli M,Feng F,Liu X,et al.On some new operation in soft set theory[J].Computers and Mathematics with Applications,2009,57:1547-1553.

[20]Won Keun Min.A note on soft topological spaces[J].Computers and Mathematics with Applications,2011,62: 3524-3528.

Separation properties in soft topological spaces

He Jiali
(School of Mathematics and Statistics,Yulin Normal University,Yulin 537000,China)

Some characters of the soft topological space are studied in this paper.The new soft point and the soft continuity are defined and the relationship discussed between it and the previous.The separation property of soft topological spaces and product topological spaces are proofed.The relationships about various separation properties are illustrated by examples,which has promoted the soft topological space further.

soft point,soft separation properties,product spaces,soft set

O153.1

A

1008-5513(2017)02-0141-11

10.3969/j.issn.1008-5513.2017.02.005

2017-03-08.

国家自然科学基金(61364020);广西青年自科基金(2014GXNSFBA118015);广西教育厅科学基金(201204LX335).

何家莉(1981-),硕士,讲师,研究方向：粗糙集等相关领域.

2010 MSC:54M10