张福玲

(渭南师范学院 数理学院 数学系，陕西 渭南 714099)

广义Fibonacci数列两项乘积倒数的有限和

张福玲

(渭南师范学院 数理学院 数学系，陕西 渭南 714099)

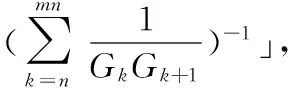
广义Fibonacci数列; 倒数; 有限和

{Fk}数列满足二次线性的递推关系Fk+2=Fk+1+Fk，F0=0，F1=1.近几年，许多学者对此数列的倒数和进行了研究，并且取得了一些研究成果.文献[1]研究了Fibonacci数列倒数的无限和

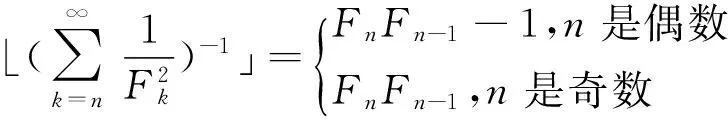
文献[2]讨论了Fibonacci数列倒数的有限和

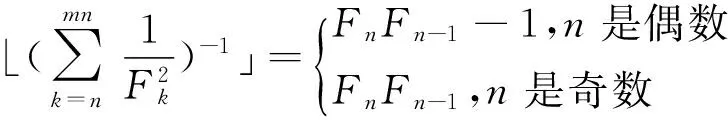
在文献[3]中证明了Fibonacci数列偶数项和奇数项倒数的有限和

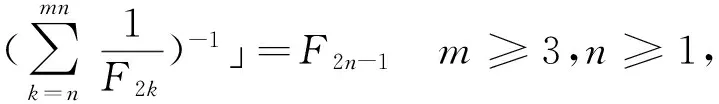
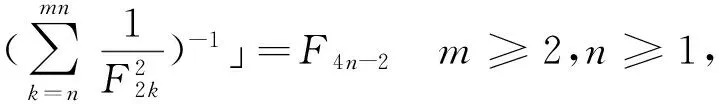
在文献[4]中得出了Fibonacci数列两项乘积倒数的有限和

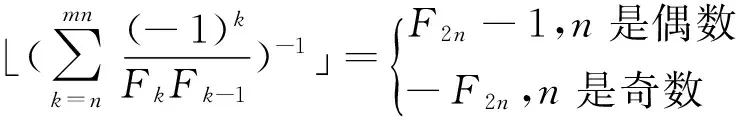
在文献[5]中给出了Fibonacci数列的子数列{F3k}有限和

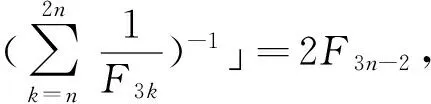
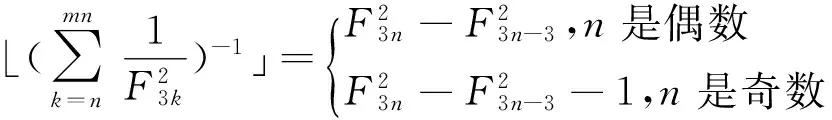
文献[6]将广义的Fibonacci定义为

Gn+2=aGn+1+Gnn≥0,G0=0,G1=1，

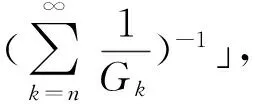
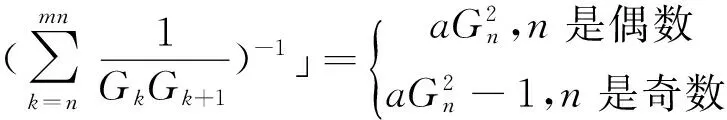
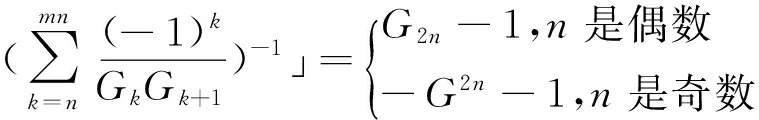
1 GkGk+1倒数和

1.1 有关引理及证明 根据广义的Fibonacci定义可得{Gn}的通项公式为

由{Gn}的通项公式可得引理1～2.

引理1GmGn-GpGq=(-1)m+1Gn-pGn-q，(n>max{p,q},m+n=p+q).

引理2GmGn+Gm+1Gn+1=Gm+n+1.

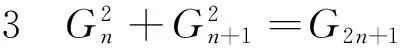
证明 由引理2，若令m=n可得.

引理4Gn-1Gn+1+GnGn+2=G2n+1.

证明 由引理2，令m=n-1,n=n+1可得.

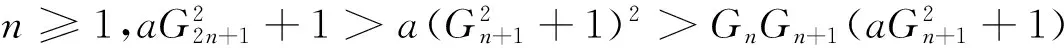
证明 由引理3可得

所以

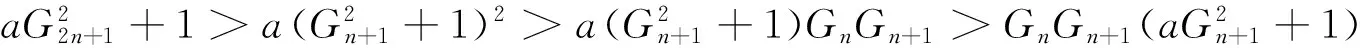
引理6Gn+1Gn+2-Gn-1Gn=aG2n+1.

证明 由引理4和广义的Fibonacci递推公式可得

G2n+1=Gn-1Gn+1+GnGn+2,

那么

aG2n+1=aGn-1Gn+1+aGnGn+2=(Gn+2-Gn)Gn-1+(Gn+1-Gn-1)Gn+2=Gn+1Gn+2-GnGn-1.

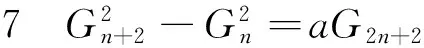
证明 由引理3可得

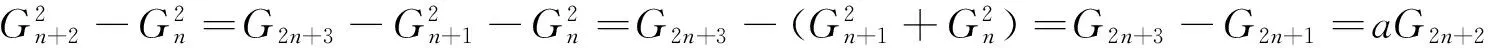
2 定理及证明

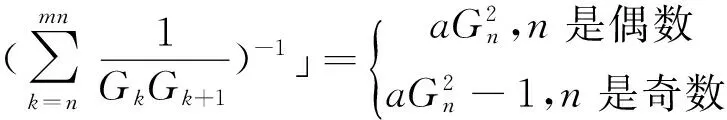
证明 根据引理1

(1)

所以

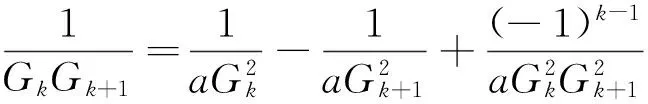
(2)

那么

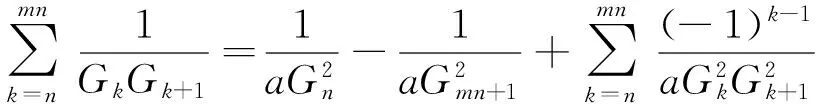
(3)

1)n为偶数

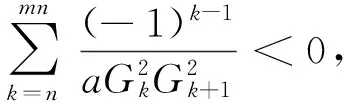
(4)

对于任意的k有

(5)

那么

所以

(6)

由式(4)和(6)可得，当n为偶数时

即当n为偶数时

(7)

2)n为奇数

对于任意的k有

(8)

所以

因此可得

(9)

根据式(3)和引理7，

由引理2和引理3可得

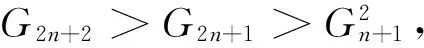
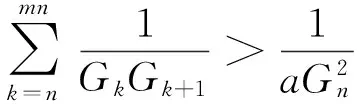
(10)

由式(9)和(10)可得，当n为奇数时

所以当n为奇数时

(11)

由式(7)和(11)可知定理1成立.

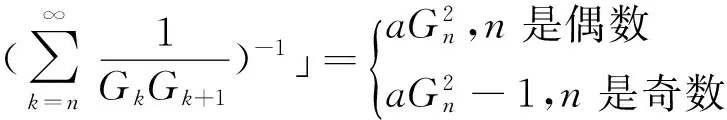
证明 1)n为偶数

由式(1)可知

所以

即

(12)

由式(5)可知

由此可得

即

(13)

由式(12)和(13)可知当n为偶数时

(14)

2)n为奇数

由式(1)可知

所以

即

(15)

由式(8)可知

由此可得

即

(16)

由式(15)和(16)可知当为奇数时

(17)

由式(14)和(17)可知推论1成立.

3 GkGk+1交错项的倒数和

3.1 有关引理及证明

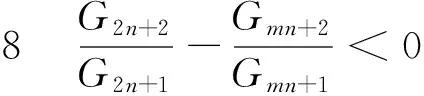
证明 由引理1可得

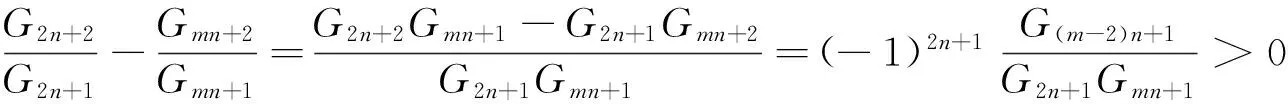
同理可得 .

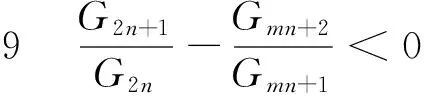
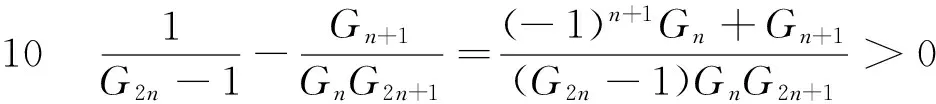
证明 由引理1 可得

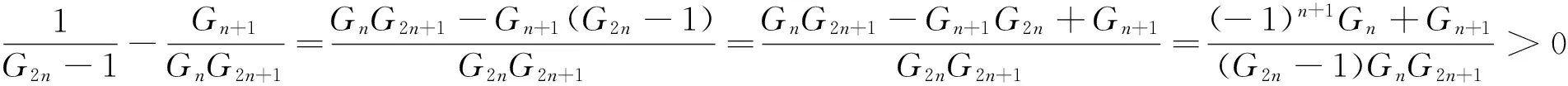
同理可得.

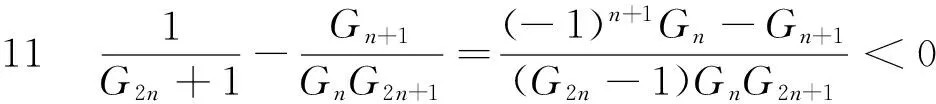
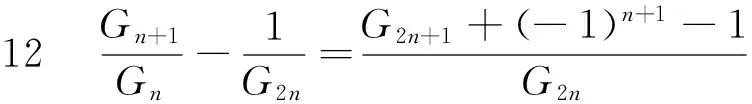
证明 由引理1，引理2和引理3可得

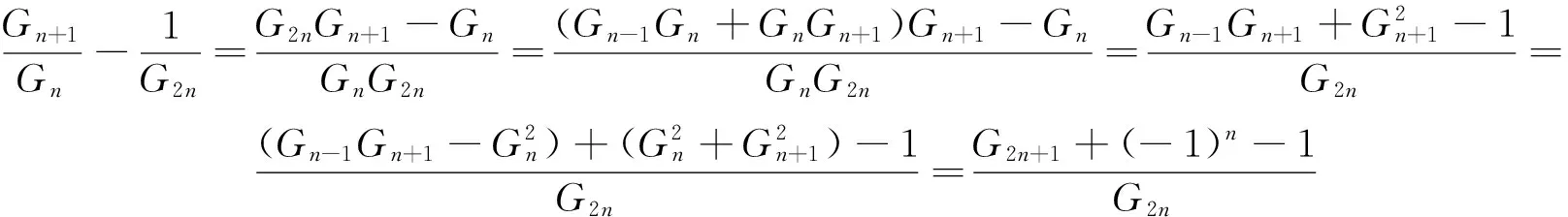
同理可得 .

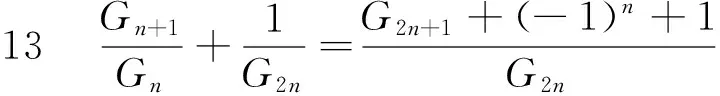
3.2 定理及证明

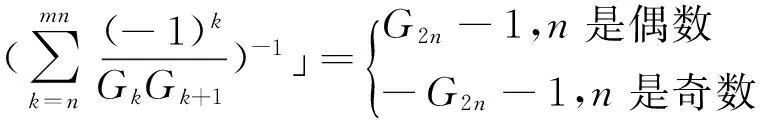
证明 引理1可得

那么

所以

(18)

1)n为偶数

由引理8和引理1可得，

根据引理10有

由引理12

根据引理9有

(20)

由式(18) ，(19)和(20)可得，若n为偶数

即若n为偶数

(21)

2)n为奇数

由引理8和引理1可得，

由引理11可得

(22)

由引理13有

所以由引理9可得

即

(23)

由式(18) ，(22)和(23) 可得若n为奇数

即若为奇数

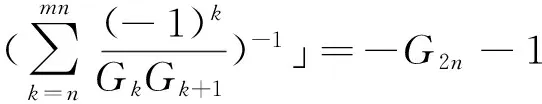
由式(21)和(24)可知定理2成立.

[1]OhtsukaH,NakamuraS.OnthesumofreciprocalFibonaccinumbers[J].FibonacciQuart，2012(2):153-159.

[2] 吴振刚，王婷婷.关于斐波那契数列倒数的有限和[J].内蒙古师范大学学报:自然科学汉文版,2011，40(2):125-128.

[3]KomatsuT,LaohakosolV.Onthesumofreciprocalofnumberssatisfyingarecurrencerelationoforders[J].JournalofIntegerSequence,2010,13(5):8-16.

[4]YeXL,ZhangZZ.OnsomeformulasofthereciprocalsumandthealternatingsumforgeneralizedFibonaccinumbers[J].AdvancedStudiesinContemporaryMathematics,2005,10(2):143-148.

[5]ZhangGJ.TheinfinitesumofreciprocaloftheFibonaccinumbers[J].JournalofMathematicalResearch&Exposition,2011,31(6):1 030-1 034.

[6]HollidayS,KomatsuT.OntheSumofReciprocalGeneralizedFibonacciNumbers[J].Integers，2011,11(4)：441-455.

Finite Sums of Reciprocal of the Products of Two Generalized Fibonacci Number

Zhang Fuling

(College of Mathematics and physics, Weinan Normal University, Weinan 714099, China)

generalized Fibonacci numbers; reciprocal; finite sum

2016-11-01

陕西省教育厅科学研究计划专项项目(2015JK1262);渭南师范学院科研基金项目(14YKP008);渭南师范学院基础数学重点学科资助

张福玲(1970-),陕西临渭区人，副教授,硕士,研究方向：数论研究，E-mail:fuling-zhang@163.com

1004-1729(2017)01-0015-07

O

ADOl：10.15886/j.cnki.hdxbzkb.2017.0004