曾 娇，邱 春，崔泽建

(1.西华师范大学 数学与信息学院，四川 南充 637009；2.四川建筑职业技术学院，四川 德阳 618000)



Boussinesq方程的精确行波解

曾 娇1，邱 春2，崔泽建1

(1.西华师范大学 数学与信息学院，四川 南充 637009；2.四川建筑职业技术学院，四川 德阳 618000)

采用一种辅助函数法求解了描述浅水波特性的Boussinesq方程，得到了其多组精确行波解。包括Jacobi椭圆函数解、Weierstrass椭圆函数解、孤波解及三角函数解，除包含以往结果，还包括一些新解。

Boussinesq方程；辅助方程法；精确解

0 引 言

Boussinesq方程常用于描述非线性浅水波的传播和变化，在海洋工程中有较为广泛的应用。为更准确的描述波的色散和非线性特征，人们相继提出了许多改进的Boussinesq方程模型[1-4]。而对于其精确解的探索有助于人们更深入的分析理解各种动力特性，大量的新方法不断被用于求解Boussinesq方程，如自平衡方法[5-6]，Jacobi椭圆函数展开法[7-8]，双曲函数法[9]，Hirota方法[10]，Backlund变换[11-12]， Darboux 变换[13-14]，各种辅助函数法在非线性方程的求解中越来越得到了广泛的应用[15-23]，该类方法一般是将待求解非线性方程与已经存在的比如投影Riccati方程、辅助常微分方程等建立关系。

1 Boussinesq方程简介

描述不可压缩、无粘流体波动特性的无量纲控制方程形式如下，

(1)

式中下标t，z表示对t，z的偏导数；▽=(∂/∂x,∂/∂y)表示二维笛卡尔坐标系中梯度算子；φ为流场的速度势；η为水面位移；ε=A/h和μ=kh为非线性和色散参数。方程(1)是在弱非线性及色散时推导而出( 即O(ε)≪1，O(μ)≪1，O(ε)=Ο(μ2))。经简单变换，得到三维Boussinesq方程形式如下：

(2)

本文中，仅讨论上式的一维情况，形式如下：

(3)

式中u为水深方向的平均速度。上式有孤波解及Jacobi椭圆余弦函数解[24]，本文中采用一种新的辅助函数法[22-23]来探索其更多的精确行波解。

2 方法介绍

设非线性演化方程一般形式如下

F(U,Uξ,Uξξ，…)=0，

(4)

式中F是其参数的多项式函数，引入行波变换ξ=x-ct，有

(5)

方程(4)可变换为

F(U，U′，U″，…)=0。

(6)

设方程(6)有如下形式的解

(7)

式中n为正整数，φ=φ(ξ)满足如下辅助常微分方程

(8)

式中p0,p2,p4为待定常数， 不同的p0,p2,p4及其对应的解见文献[17，21-22]。

3 Boussinesq方程的精确行波解

引入行波变换

η(x,t)=η(ξ),u(x,t)=u(ξ),ξ=x-ct，

(9)

式中c为波速。将(9)式及(5)式代入(3)式有

(10)

式中“′”表示对ξ的一阶导数。将(10)式对ξ积分一次得到

(11)

式中C1和C2为积分常数。由(11)式的第二式得到

(12)

将式(12)代入(11)式的第一式得到关于ξ的常微分方程

(13)

引入

(14)

则方程(13)可改写为

Au″+Buu″+Cu3+Du2+Eu+G=0。

(15)

将方程(15)的解记为

(16)

由方程(15)中U的非线性项和最高阶导数项平衡可知n=1，因此(16)式可表示为

u(ξ)=a0+a1φ(ξ)，

(17)

式中a0，a1为待定常数，φ(ξ)满足方程(8)。

将方程(17)及(8)代入方程(15)并令φ(ξ)i(i=1,2,…)的系数为零，有如下代数方程组

(18)

借助于Mathmatica计算机软件可得到如下非平凡解：

说明1：在解(a4)—(a7)中，对系数a1没有限制，其为任意常数时，解均可满足方程组(18)。

将解(a1)和(a2)代入(17)式并结合φ的表达式可得出方程(15)式对应的如下精确解

(b1)

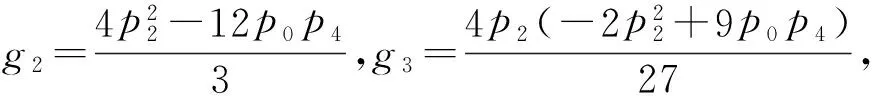
(b2)

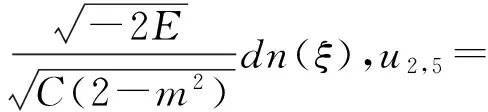
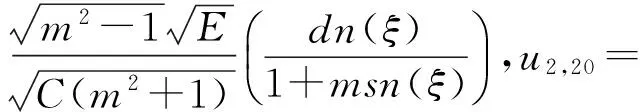
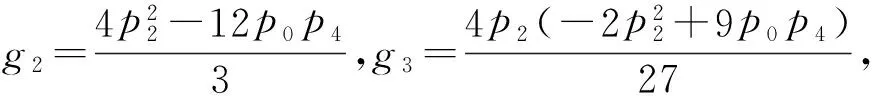
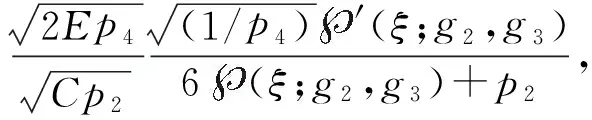
由解(a3)确定的解形式与解(a1)类似，只是C和A形式不同，此处不再分别列出。

(b3)

由解(a4)—(a7)见p4=0，因此方程(8)变为

(19)

将式(a4)—(a7)代入(17)并结合方程(19)中的解φ的表达式有：

(b4)

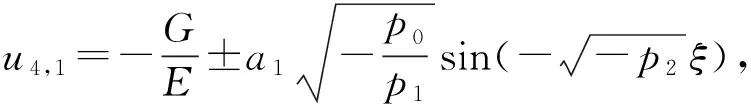
(b5)

(b6)

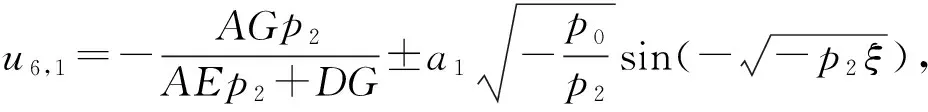
(b7)

说明2：

1. 此处仅列出u的解形式，将其代入(12)即可得到η的表达式，由于篇幅的限制，其具体形式不再列出。

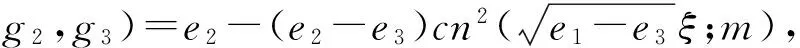
3. 在解(1,3,6,7)中B=0或C=0表示忽略小量, 这对于实际物理情况是可以理解的，在解(2,4,5)中，D=0表示忽略主要非线性项。

4 结 论

本文基于辅助微分方程求解了具有弱非线性及色散特性的Boussinesq方程，给出多组精确行波解，这些精确解将有助于理解浅水波的物理机制及相应的动力特性，此方法也有助于我们探索其它非线性演化方程的新解。

[1] CHEN C L,LOU S Y,LI Y S.Solitary wave solutions for a general Boussinesq type fluid model[J].Commun Nonlinear Sci Numer Simulat,2004,9:583-601.

[2] WAZWAZ A M.New travelling wave solutions to the Boussinesq and the Klein-Gordon equations[J].Commun Nonlinear Sci Numer Simulat,2008,13:889-901.

[3] JAVIDI M,JALILIAN Y.Exact solitary wave solutions of Boussinesq equation by VIM[J].Chaos Solitons&Fractals,2008,36(5):1256-1260.

[5] MOHAMMED KHALFALLAH.New exact traveling wave solutions of the (3+1) dimensional Kadomtsev-Petviashvili (KP) equation[J].Commun Nonlinear Sci Numer Simulat，2009,14(4):1169-1175.

[6] 詹 雨,白 慧,斯 琴.齐次平衡法与Burgers-Huxley方程的精确解[J].河套学院学报,2013(2):80-87.

[7] LIU S K,FU Z T,LIU S D,Q，et al.Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J].Phys Lett A,2001,289(1):69-74.

[8] YAN Z Y.Abundant families of Jacobi elliptic function solutions of (2+1) dimensional integrable Davey-Stewartson-type equation via a new method[J].Chaos Solitons Fractals,2003,18(2):299-309.

[9] 刘雪梅,接 贤.利用推广的Tanh函数法求解两个非线性发展方程[J].中国民航大学学报,2015，33(4):56-58,64.

[10] WAZWAZ A M.Multiple soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh-coth method[J].Appl.Math.Comput.,2007,190(1):633-640.

[11] ABLOWITZ M J,CLARKSON P A.Solitons:nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1991.

[12] MIURA M R.Backlund transformation[M].Berlin: Springer-verlag,1978.

[13] MATVEEV V A,SALLE M A.Darboux transformation and solitons[M].Berlin:Springer,1991.

[14] LI Y S,MA W X,ZHANG J E.Darboux transformations of classical Boussinesq system and its new solutions[J].Phys.Lett.A,2000,275(1):60-66.

[15] 邱 春,刁明军,徐兰兰,等.构造非线性演化方程精确解的一个新方法[J].量子电子学报，2012，29(3):279-285.

[16] 套格图桑,斯仁道尔吉.构造变系数非线性发展方程精确解的一种方法[J].物理学报,2009，58(4):2121-2126.

[17] YAN Z Y.An improved algebra method and its applications in nonlinear wave equations[J].Chaos Solitons Fractals,2004,21(4):1013-1021.

[18] YOMBA E.The extended Fan’s sub-equation method and its application to Kdv-MKdv BKK and variant Boussinesq equations[J].Phys Lett A,2005,336(6):463-476.

[19] HON Y C,FAN E G.A series of exact solutions for coupled Higgs field equation and coupled Schrodinger-Boussinesq equation[J].Nonlinear Analysis,2009,71(7):3501-3508.

[20] GAO L.MA W X,XU W.Travelling wave solutions to Zufiria’s higher-order Boussinesq type equations[J].Nonlinear Analysis,2009,71(12):e711-e724.

[21] GUO Y X,LAI S Y. New exact solutions for an (N + 1)-dimensional generalized Boussinesq equation[J].Nonlinear Analysis,2010,72(6):2863-2873.

[22] LI H M.New exact solutions of nonlinear Gross-Pitaevskii equation with weak bias magnetic and time-dependent laser fields[J].Chin.Phys.,2005,14(2):251-256.

[23] LIU Y P,LI Z B.An automated algebraic method for finding a series of exact travelling wave solutions of nonlinear evolution equations[J].Chin.Phys.Lett.,2003,20(3):317-320.

[24] 梅强中.水波动力学[M].北京:科学出版社,1984.

Exact Travelling Wave Solutions of Boussinesq Equation

ZENG Jiao1,QIU Chun2,CUI Zejian1

(1.College of Mathematics and Information,China West Normal University,Nanchong Sichuan 637009,China; 2.Sichuan College of Architectural Technology,Deyang Sichuan 618000,China)

In this paper,we used the auxiliary function method to solve the Boussinesq equation,which describes the shallow potter,and we got a series of exact travelling wave solutions,including the Jacobi elliptic function solutions,Weierstrass elliptic function solution,solitary wave solutions and triangle function solutions,which not only contains the existed results,but also include some new solutions.

Boussinesq equation;auxiliary equation method;the exact solution

1673-5072(2016)04-0412-07

2016-04-12

四川省教育厅自然科学重点项目(09ZA119)

曾 娇(1991—),女,四川隆昌人,硕士研究生,主要从事偏微分方程研究。

崔泽建(1963—),男,四川南充人,教授,主要从事偏微分方程研究。 E-mail: cuizejian@126.com

O175

A

10.16246/j.issn.1673-5072.2016.04.010