元素最小描述并集下的概率粗糙集模型及其决策
2016-10-13蔡克参刘财辉
蔡克参*,刘财辉
元素最小描述并集下的概率粗糙集模型及其决策
蔡克参*,刘财辉
(赣南师范大学数学与计算机科学学院,江西赣州,341000)
基于元素的最小描述并集,本文提出了一种新的概率粗糙集模型。针对新模型设计了相应算法来计算元素最小描述并集及相应条件概率。最后通过一个实例,比较了已有模型和新模型在决策中的应用,结果表明新模型更具有合理性。
粗糙集;覆盖;最小描述;概率粗糙集;决策粗糙集
引言
粗糙集理论[1]是Pawlak于1982年提出的一种新的处理模糊和不确定性知识的数学工具。随着粗糙集理论研究的不断深入,粗糙集的研究领域不断被拓宽。目前人们研究较多的粗糙集模型有:覆盖粗糙集、概率粗糙集、决策粗糙集、多粒度粗糙集等。覆盖粗糙集的概念是Bonikowski[2]从实际应用出发利用论域上的覆盖关系对粗糙集进行推广,与覆盖粗糙集结合的研究内容很广泛,文献[3]研究了覆盖粗糙集与决策模型之间的结合运用。许多学者对覆盖粗糙集中的最大、最小描述概念在粗糙集进行了研究。文献[4]用矩阵的方法对最大、最小描述进行了计算,文献[5-6]在覆盖广义粗糙集理论中,对最小描述的定义进行了讨论,集合并拓展了多粒度覆盖粗糙集模型;文献[7]给出了基于最小描述交的覆盖近似算子,丰富了覆盖粗糙集理论;文献[8]研究了最小描述与模糊集中隶属度的关系,建立了一个新的覆盖粗糙集模型。概率粗糙集[9]是Pawlak粗糙集模型的一种推广形式,经典的概率粗糙集模型是基于等价关系建立的,文献[10-11]提出了新的概率粗糙集模型,文献[12-13]对不同模型下的概率粗糙集模型算法进行了分析。决策粗糙集模型是Yao等人[14]1990年提出的,文献[15-17]对原有的概率粗糙集模型进行了拓广,提出了几种新的决策粗糙集模型,文献[18-19]很好的融合了粗糙集理论和决策理论,方便了实际的决策运用,文献[20]总述了决策粗糙集的研究现状。
一般情况下基于等价关系的粗糙集模型,往往受限较多,在决策中往往决策结果也不太理想。针对这一问题,已经有学者建立了基于覆盖关系的概率粗糙集模型,讨论了元素最小描述交集在概率粗糙集模型中的决策及运用。受此启发,本文将覆盖粗糙集中最小描述与概率粗糙集、决策粗糙集相结合,提出了一种元素最小描述并集下的决策粗糙集模型。该模型对原有的概率粗糙集模型进行了拓展,并结合具体的实例进行了新模型合理性的说明。
1 基本概念
定义1[21]给定一个覆盖近似空间,其中是论域,是的一个覆盖。对任意的,称

定义2[9]设是非空有限论域,集函数称为概率测度,若:

定义3[9]设是有限论域,是上的概率测度,,称为事件发生条件下事件发生的条件概率。
定义 4[9]给定非空有限子集,为论域上的等价关系。论域上的一个划分。对,Pawlak粗糙集的正域,边界域和负域,其定义分别为:

(4)
这样,就得到了Pawlak三个域的另一种表示:

定义 5[9]对,令,则概率粗糙集的-正域、负域和边界域可定义为:
(6)
2 元素最小描述并集下的概率粗糙集模型
本节主要结合以上所给定义,对概率粗糙集模型进行拓展,给出了基于元素最小描述并的概率粗糙集模型,并对其性质及求解过程进行了分析。
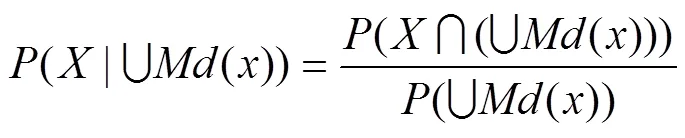
为元素最小描述并集下的条件概率。
下面结合算法对所给定义进行分析说明。设计算法使用了JAVA语言,程序运行环境是myeclipse 8.5,限于文章篇幅,下面只给出算法的主要思想及核心部分的代码。
2.1 计算元素最小描述并集算法设计
该算法的主要运用两个嵌套的for循环,找出同时包含某个共同元素的集合,比较集合间的包含关系,取被包含的集合作为输出对象,循环输出结果,求出元素最小描述。再求出每个元素对应的最小描述集合内所有元素的并集;核心代码如下:
//求元素最小描述
for (String variable : variaList){
List
for (int i = 0; i < variaCollections.size();i++){
Set
if (variaCollection.contains(variable)){ variaReflectCollection.add(variaCollection);
for (int j = 0; j < variaCollections.size() ;j++){
if (j != i) { Set
if (variaCollection.containsAll(chirldVariaCollection) && chirldVariaCollection.contains(variable)){
variaReflectCollection.remove(variaCollection);
}}}}}
variaIncludedRelationships.put(variable, variaReflectCollection);
}
return variaIncludedRelationships;
//最小描述内部元素取并集
public static Map
Map
for (Map.Entry
List
Set
System.out.println("元素" + entry.getKey() + " 对应的最小描述: " + entry.getValue() + " 对应的自并集合为: " + intersection); intersections.put( entry.getKey(),intersection);
}
return intersections;
}
2.2 元素最小描述并集下的条件概率算法设计
本算法的设计调用了上面的最小描述并集算法,主要分以下几个步骤进行:
步骤1 调用intersection()集合求交集函数,求出给定集合与最小描述并集中集合的相交集合;
步骤2 取步骤1所得集合与最小描述并集合元素个数的比值;
步骤3 使用System.out.println输出条件概率。
主要部分代码如下:
//取并集后的集合与给定集合取交集
String[ ] pointArray = {"x1","x2","x3","x4"};
Set
public static Set
Set
intersectionSet.clear();
for (int i = 0; i < variaCollections.size();i++){
Set
if (i == 0) intersectionSet.addAll(variaCollection);
else
intersectionSet.retainAll(variaCollection);
}
return intersectionSet;
}
//求两个集合元素个数的比值
public static Set
Set
intersectionSet.clear();
intersectionSet.addAll(set1);
intersectionSet.retainAll(set2);
return intersectionSet;
}
public static String probability(Set
Set
return set1.size()+"/"+set2.size();
}
//输出各元素对应的概率
System.out.println("元素" + entry.getKey() + " 对应的最小描述: " + entry.getValue() + " 的条件概率为:" + probability);
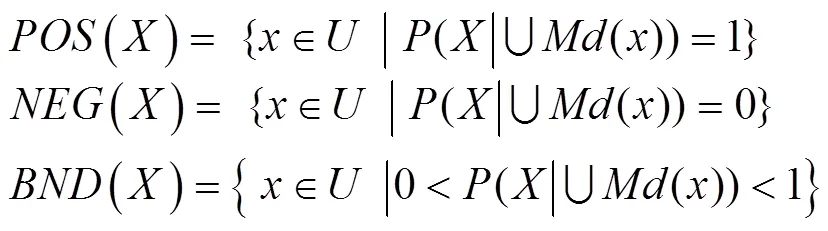
(9)
3 两种概率粗糙集模型下的决策情形
本节主要使用上一节提出的基于元素最小描述并集的概率粗糙集模型,并结合一般的基于等价关系建立的概率粗糙集模型,对Pawlak粗糙集、0.5-概率粗糙集和概率粗糙集共三种粗糙集模型进行决策。比较以上两种概率粗糙集模型下三种粗糙集的决策情形。
下面通过案例对比两种不同情况下的决策模型。

表1 病症表现
a) 基于等价关系的概率粗糙集决策模型
(3)等价关系下的条件概率:
(4)根据以上计算所得条件概率,可做出决策如下,决策结果见表2:
表2 基于等价关系的决策情形(令= 0.4,= 0.75)
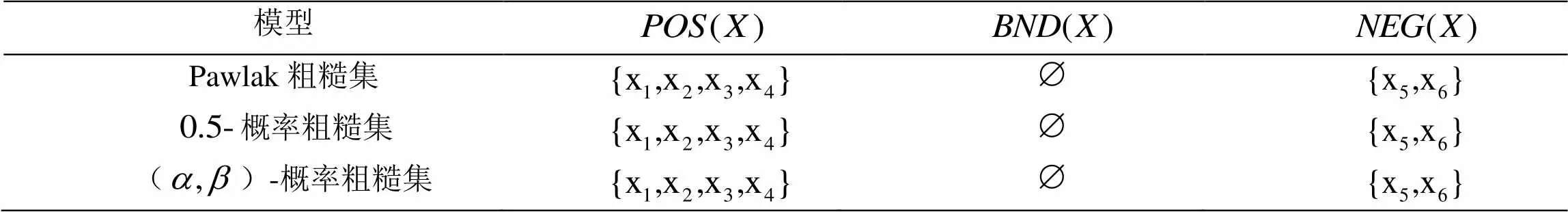
模型 Pawlak粗糙集 概率粗糙集 ()-概率粗糙集
3.2 元素最小描述并集下的概率粗糙集决策模型
(1) 对论域中的对象根据病症分类如下:
(2) 论域U的一个覆盖:
(3)程序运行元素最小描述结果如下:
(4)程序运行元素最小描述并集下的条件概率结果如下:
(5)根据以上计算所得条件概率,可以做出如下决策,决策结果见表3:

表 3 元素最小描述并集下的决策情形(设β= 0.4,α= 0.75)
4 结语
本文设计算法并计算了元素最小描述并集下的条件概率,分析了一般基于等价关系的概率粗糙集模型进行决策的弊端。对一般的概率粗糙集模型进行优化,给出了基于元素最小描述并集的决策粗糙集模型,并结合应用实例对两种模型的决策结果进行了比较。
[1] Pawlak Z.Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5):341-356.
[2] Zakowski B W. Approximations in the space (U, Ⅱ)[J]. Demonstration Mathematical,1983,16:761-769.
[3] 薛占熬, 刘杰, 朱泰隆. 基于覆盖的Sugeno测度粗糙集模型及其三支决策[J]. 计算机科学, 2016, 43(3): 285-290.
[4] 林姿琼, 王敬前, 祝峰. 矩阵方法计算覆盖粗糙集中最小、最大描述[J]. 山东大学学报(理学版),2014,49(8):97-101.
[5] 黄婧, 李进金.最小描述的多粒度覆盖粗糙集模型[J].计算机工程与应用, 2013, 49(9): 134-149.
[6] 刘财辉,涂小强. 条件概率描述下的多粒度覆盖粗糙集模型研究[J].计算机科学, 2015, 42(6):88-92.
[7] 张晓燕, 徐伟华, 张文修. 基于最小描述交的覆盖广义粗糙集[J].模糊系统与数学, 2011, 25(2):146-155.
[8] 汤建国,佘堃, 祝峰. 一种新的覆盖粗糙模糊集模型[J].决策与支持, 2012,27(11):1653-1662.
[9] 张文修, 吴伟志, 梁吉业, 李德玉. 粗糙集理论与方法[M].北京:科学出版社, 2001.
[10] 巩增泰, 史战红. 基于覆盖的概率粗糙集模型及其Bayes决策[J]. 模糊系统与数学,2008,22(4):142-148.
[11] 巩增泰, 柴润丽. 基于区间值模糊概率测度的多粒度区间值决策粗糙集模型[J]. 西北师范大学学报: 自然科学版, 2015, 51(6): 21-27.
[12] 王红, 张燕平, 钱付兰等. EM 最优参数求解的概率粗糙集推荐算法[J]. 计算机科学与探索, 2016, 10(2): 285-292.
[13] 王辉, 黄自威, 刘淑芬. 新型加权粗糙朴素贝叶斯算法及其应用研究[J]. 计算机应用研究, 2015, 32(12):3668-3672.
[14] Yao Y Y,Wong SKM.,LingrasP. A decision-theoretic rough set model // RasZW, Methodologies for IntelligentSystems,vol.5.New York:North-Holland, 1990:17-24.
[15] 李华雄, 刘盾, 周献中. 决策粗糙集模型研究综述[J]. 重庆邮电大学学报(自然科学版), 2010,22(5):624-630.
[16] 赵文清, 朱永利, 高伟. 一个基于决策粗糙集理论的信息过滤模型[J].计算机工程与应用, 2007,43(7):185-187.
[17] 衷锦仪, 叶东毅. 基于模糊数风险最小化的拓展决策粗糙集模型[J]. 计算机科学, 2014,41(3):50-54.
[18] 刘盾, 李天瑞, 李华雄. 粗糙集理论: 基于三支决策视角[J].南京大学学报(自然科学版),2013,49(5):574-581.
[19] 刘盾, 李天瑞, 李华雄. 区间决策粗糙集[J]. 计算机科学,2012,39(7):178-181.
[20] 于洪, 王国胤, 姚一豫. 决策粗糙集理论研究现状与展望[J]. 计算机学报, 2015, 38(8): 1628-1639.
[21] Zhu W,Wang F Y.Reduction and axiomization of covering generalized rough sets [J]. Information Sciences, 2003, 152:217-230.
Probabilistic Rough Set Model Based on the Union of Minimal Descriptions of Elements and Its Applications
CAI Kecan , LIU Caihui
(Department of Mathematics and Computer Science, Gannan Normal University, Ganzhou Jiangxi 341000, China)
This paper proposed a new kind of probability rough set based on the union of minimal description of elements. Some algorithms are designed for the proposed model to compute the union of minimal description of elements and corresponding probabilities. Finally, an example is employed to compare the feasibility between the existing model and the proposed model.
Rough sets; Covering; Minimal description; Probability rough sets; Decision-theoretic rough sets
1672-9129(2016)01-0048-05
TP18
A
2016-06-14;
2016-06-24。
国家自然科学基金资助项目(61305052)。
蔡克参(1992-),女,江西抚州人,硕士研究生,主要研究方向:粒计算方法在农业信息化中的应用;刘财辉(1979-),男,江西于都人,副教授,博士,主要研究方向:粗糙集、粒计算、机器学习、数据挖掘等。
(*通讯作者电子邮箱:1208008641@qq.com)
