潘柏松　谢少军　蒋立正

浙江工业大学,杭州,310014



非独立区间变量和随机变量下的单步可靠性计算方法

潘柏松谢少军蒋立正

浙江工业大学,杭州,310014

随机变量和非独立区间变量往往共存，两种变量共存不仅导致出现双层优化问题，而且会降低可靠性的计算效率。为解决双层优化问题和提高可靠性计算效率，基于椭球模型描述的非独立区间变量，利用高维模型表示方法(HDMR)解耦随机变量和非独立区间变量，转换双层优化问题为简单的单步求解问题，基于提出的采样方法，利用二次多项式近似HDMR展式，将隐式的单步求解问题转化为显式问题，提出了一种混合型单步可靠性计算方法。算例结果表明，所提出的单步可靠性计算方法具有较高的计算效率和精度；该方法仅需少量的极限状态函数调用次数，即可获得较高精度的计算结果。

椭球模型;非独立区间变量;高维模型表示方法;快速可靠性方法

0　引言

在机械系统可靠性设计过程中，知识、试验条件、时间及经费等因素的限制，使得某些不确定性变量的统计信息不足，这导致不确定性变量的分布类型及分布函数不能被精确给定。这类因信息不足引起的不确定性被称为认知不确定性。不同于随机不确定性，认知不确定性可随信息量或知识的增加而减小甚至消失[1]。因此，在可靠性工程中，认知不确定性和随机不确定性往往共存。研究表明[2]，认知不确定性对可靠性分析及设计结果的精度存在较大影响。

为定量描述认知不确定性变量，克服认知不确定性引起的可靠性分析及设计结果精度失真，目前已发展了多种不同类型的建模理论，分为概率建模理论和非概率建模理论，其中，概率建模理论主要为贝叶斯理论[3],非概率建模理论包括可能性理论[4]、证据理论[5]和凸集模型[6]。作为凸集模型特例的区间模型[7]是指在实数轴上规定认知不确定性变量可变区间的上下限。在本文中，基于区间模型描述的认知不确定性变量称为区间变量。在工程应用中，区间变量十分常见。因此，区间变量和随机变量共存条件下的混合型可靠性研究具有重要的学术价值及工程应用价值。

目前已有较多的处理独立区间变量的可靠性分析方法[7-11]，但在实际工程中，某些区间变量存在一定的相关性，是非独立的。例如描述结构几何尺寸的区间变量和结构质量的区间变量一般存在相关性，较大的几何尺寸区间变量意味着较大结构质量区间变量，反之亦然。为此，Du[12]针对机构运动副，基于物理关系式推导获得非独立区间变量描述模型——等式与不等式约束条件，提出了一种随机变量和非独立区间变量的混合型可靠性设计方法。Jiang等[13]采用多维度平行六面体区间模型，考虑了区间变量为独立或非独立的情况，提出了一种新的非线性区间规划方法，但该规划方法未考虑系统中同时存在随机变量和区间变量的混合情况。Jiang等[14]引入样本相关系数，考虑非独立概率-区间混合情况，利用矩阵变换将非独立变量转换为独立变量，提出了一种双层迭代算法。姜潮等[15]通过引入相关角的概念定量描述了任意两个变量之间的相关性，将不同变量之间的相关性在一个统一的框架下度量，并构建了一高效求解方法。但上述的可靠性分析方法仍为双层优化问题，影响计算效率。故在非独立区间变量下，提出一种单层可靠性计算方法，提高可靠性分析的计算效率仍是当前可靠性分析方法研究的一大挑战。

为此，本文针对系统输入变量存在随机变量和非独立区间变量的混合情况，基于条件概率法和椭球模型，建立了混合型可靠性分析模型，提出了一种高效的单步可靠性模型及单步可靠性计算算法。利用高维模型表示方法[16](HDMR)解耦随机变量和非独立区间变量，将混合型可靠性分析模型转换为单步求解的可靠性分析模型；基于提出的采样方案，利用二次多项式近似HDMR展式，降低极限状态函数的调用次数，提高计算效率。

1　椭球模型

为描述非独立区间变量，Ben-Haim等[6，17]提出了椭球模型。设Y=(Y1,Y2,…,YNY)T为区间变量的矢量，其中NY为区间变量的数量。在复杂机械系统中，区间变量的维度一般较高，非独立关系也不尽相同，如某些区间变量服从正相关关系，某些满足负相关关系，而某些是相互独立的。椭球模型根据不同的非独立关系，将区间变量归入不同的组。

经分组后，Y可表示为Y=(Y1,Y2,…,YNg)T，其中，Ng为组的数量，Yi为第i组区间变量矢量，则椭球模型为

i=1,2,…,Ng)

(1)

多椭球模型可描述不同非独立关系的区间变量：如当某区间变量是独立的，则椭球模型可退化为区间模型；当两个区间变量存在相关性，则椭球模型可退化为椭圆模型。图1给出了3个区间变量构成的不同几何形状的可行域S：在图1a中，3个变量是相互独立的；在图1b中，Y3是独立的变量，Y1和Y2存在相关性，是非独立的；在图1c中，3个变量存在相关性，是非独立的。

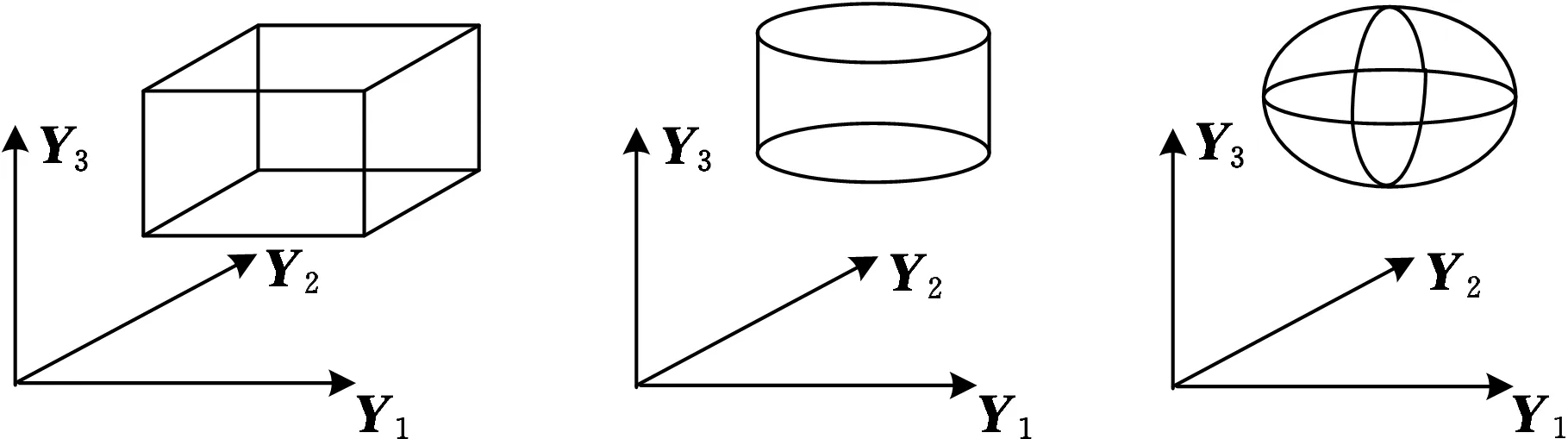
(a)Y1、Y2、Y3相互独立　　　(b)Y3独立，Y1、Y2相关(c)Y1、Y2、Y3相关图1　椭球模型

由于各个区间变量的单位不同，区间大小不同，不利于数值计算的稳定性，因此将区间变量Yi转换为量纲一变量Vi，转换关系式为

(2)

则分组后的区间变量矢量Y=(Y1,Y2,…,YNg)T转换为V=(V1,V2,…,VNg)T，多椭球模型相应地表示为

(3)

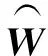
式(3)给出的椭球模型主轴与坐标轴存在角度偏移，为使样本点尽可能多地落在椭球模型可行域内，提高二次多项式近似精度，引入线性变换

(4)

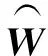
(5)

2　混合型可靠性计算模型

设系统极限状态函数为

G=g(X,Y)

(6)

其中，X=(X1,X2,…,XNX)T为随机变量矢量，随机变量的个数为NX；Y=(Y1,Y2,…,YNY)T为区间变量矢量，区间变量的个数为NY。将区间变量的变换关系式代入式(6)，则极限状态函数可写为G=g(X,E)。

设G<0时系统失效，则系统失效概率pf可表示为pf=Pr{g(X,E)<0}，其中Pr{·}表示概率。因未知区间变量E的概率分布，不能获得准确的失效概率。利用条件概率公式，可得失效概率的最小值pf，min和最大值pf，max的计算公式：

pf，min=Pr{gmax(X,E)<0|E∈S}

(7)

pf，max=Pr{gmin(X,E)<0|E∈S}

(8)

其中，gmax(X,E)和gmin(X,E)分别表示在可行域S内极限状态函数的全局最大值和最小值。

由式(7)和式(8)可见，系统失效概率的最小值和最大值分别为最大极限状态函数和最小极限状态函数的失效概率。这本质上为一个双层循环求解问题：内循环为区间分析，在可行域S内搜寻极限状态函数的极限值；外循环为概率分析，求解最大极限状态函数或最小极限状态函数的失效概率。

双层循环增加了可靠性分析问题的复杂性，会大幅度增加极限状态函数的调用次数。对于复杂机械系统，极限状态函数一般由计算机数值仿真模型(如有限元模型、流体动力学模型等)隐式表述，极限状态函数调用次数的增加,会导致计算效率低下，增大可靠性分析及设计的难度。

为提高随机变量和非独立区间变量混合情况下的可靠性计算效率，本文采用高维模型表示方法，将双层循环问题转化为单步问题，提出了一种单步快速的可靠性计算方法。

2.1高维模型表示方法(HDMR)

高维模型表示方法是一种用于模型近似的处理方法，它常用于近似高维度输入系统的响应函数。研究表明，低阶的高维模型表示方法可精确描述大部分工程中的极限状态函数[18]。

本节主要介绍如何采用HDMR描述极限状态函数g(X,E)。设Z=(X,E)T，则g(X,E)可写为g(Z)。基于高维模型表示方法，g(Z)可表示为

(9)

其中，NZ为Z向量的元素个数，NZ=NX+NY；g0为0阶分量函数，为常量；gi(Zi)为1阶分量函数，表示输入变量Zi单独作用时对输出响应g(Z)的影响；gij(Zi,Zj)为2阶分量函数，表示输入变量Zi和Zj共同作用时对输出响应g(Z)的影响；更高阶的分量函数表示多个输入变量共同作用时对输出响应g(Z)的影响；最后一项g12…NZ(Z1,Z2,…,ZNZ)表示所有残余的耦合输入变量对输出响应的影响。

切割法(cut-HDMR)是一种确定高维模型各个分量函数的常用方法。在切割法中，首先选定参考点c，再计算经过参考点c的线、平面、体积等切割几何上的响应值，分别确定各个分量函数。实际使用中，参考点c一般选定为输入变量可行空间内最感兴趣的点。

利用切割法，各分量函数可表示为

g0=g(c)

(10)

gi(Zi)=g(Zi,ci)-g0

(11)

gij(Zi,Zj)=g(Zi,Zj,cij)-gi(Zi)-gj(Zj)-g0

(12)

其中，g(Zi,ci)=g(c1,c2,…,ci-1,Zi,ci+1,…,cl) ，表示除了分量Zi，其余所有输入变量均固定在参考点c处，它是一个一元函数；类似地，g(Zi,Zj,cij)为二元函数；最后项g12…l(Z1,Z2,…,Zl)由真实响应值和基于高维模型表示方法的预测值的残差确定。

在高维模型表示方法中，1阶、2阶、3阶等分量函数与泰勒级数展开式中相应的分量函数有着本质区别。经证明，高维模型表示方法中的1阶分量函数gi(Zi)是泰勒级数展开式中仅含有变量Zi分量函数的集合；类似地，2阶分量函数gij(Zi,Zj)是泰勒级数展开式中仅含有变量Zi和Zj分量函数的集合。1阶分量函数gi(Zi)可以是非线性的。因此，较截断的泰勒级数展式，任意相应截断的高维模型表示方法的展式具有较高的精度。

2.2单步可靠性计算模型

若极限状态函数可描述为关于随机变量和区间变量相互分离的两部分函数，则双层循环问题可变为单层问题，提高计算效率。

利用1阶HDMR展式，极限状态函数可近似为

(13)

如前所述，1阶HDMR展式gi(Xi)和gi(Ei)分别是泰勒展式内仅含有变量Xi和Yi所有分量函数的集合,因此，相对于1阶泰勒展式，1阶HDMR展式没有限定近似表达式的非线性。这提高了1阶HDMR展式的近似精度。

基于1阶HDMR展式的近似表达式，失效概率的最小值和最大值的计算模型可写为

pf，min=Pr{Gmax=(1-NX-NY)g0+

(14)

pf,max=Pr{Gmin=(1-NX-NY)g0+

(15)

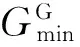
(16)

(17)

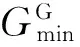
3　计算失效概率

使用单步可靠性计算模型计算失效概率上下限时，需确定参考点c和各个一元函数表达式。参考点c对可靠性计算结果的精度具有一定的影响。为提高精度，参考点c一般选定为输入变量可行空间内最感兴趣的点。区间变量的可行区间往往较小，区间变量可行区间内的中点可兼顾两个边界点，为此，将区间变量可行区间内的中点及区间变量固定在中点时的最大概率点(MPP)对应的随机变量值设定为参考点c。

最大概率点u*的数学计算模型为

(18)

s.t.g(U,0)=0

其中，U=(U1,U2,…,UNX)T为独立的随机变量矢量，服从标准正态分布，由随机矢量X经Rosenblatt变换获得。

一旦求得MPP，则参考点c为

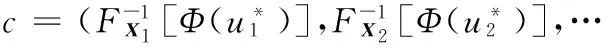
(19)

基于求得的参考点c，使用二次多项式近似表达各个一元函数表达式。设gi(Xi,ci)和gi(Ei,cn+i)的近似式分别为

(20)

(21)

其中，ai0、ai1、ai2、bi0、bi1和bi2分别为二次多项式的待定系数。

采用最小二乘法求解各个二次多项式的待定系数。在最小二乘法中，对于随机变量Xi，沿过参考点c的Xi轴，在[μi-3σi,μi+3σi]区间内均匀分布k(k=5，7，9)个样本点，如图2所示，其中μi和σi分别为随机变量Xi的均值和标准差。各个样本点的坐标值为μi-3σi，μi-3σi+6σi/(k-1)，…，μi，μi+6σi/(k-1)，…，μi+3σi。对于变换后的区间变量Ei，沿过参考点c的Ei轴，在[-1,1]区间内均匀分布k(k=5，7，9)个样本点，如图2所示。各个样本点的坐标值为-1，-1+2/(k-1)， …，0，2/(k-1)，…，1。

(a)随机变量的样本点分布

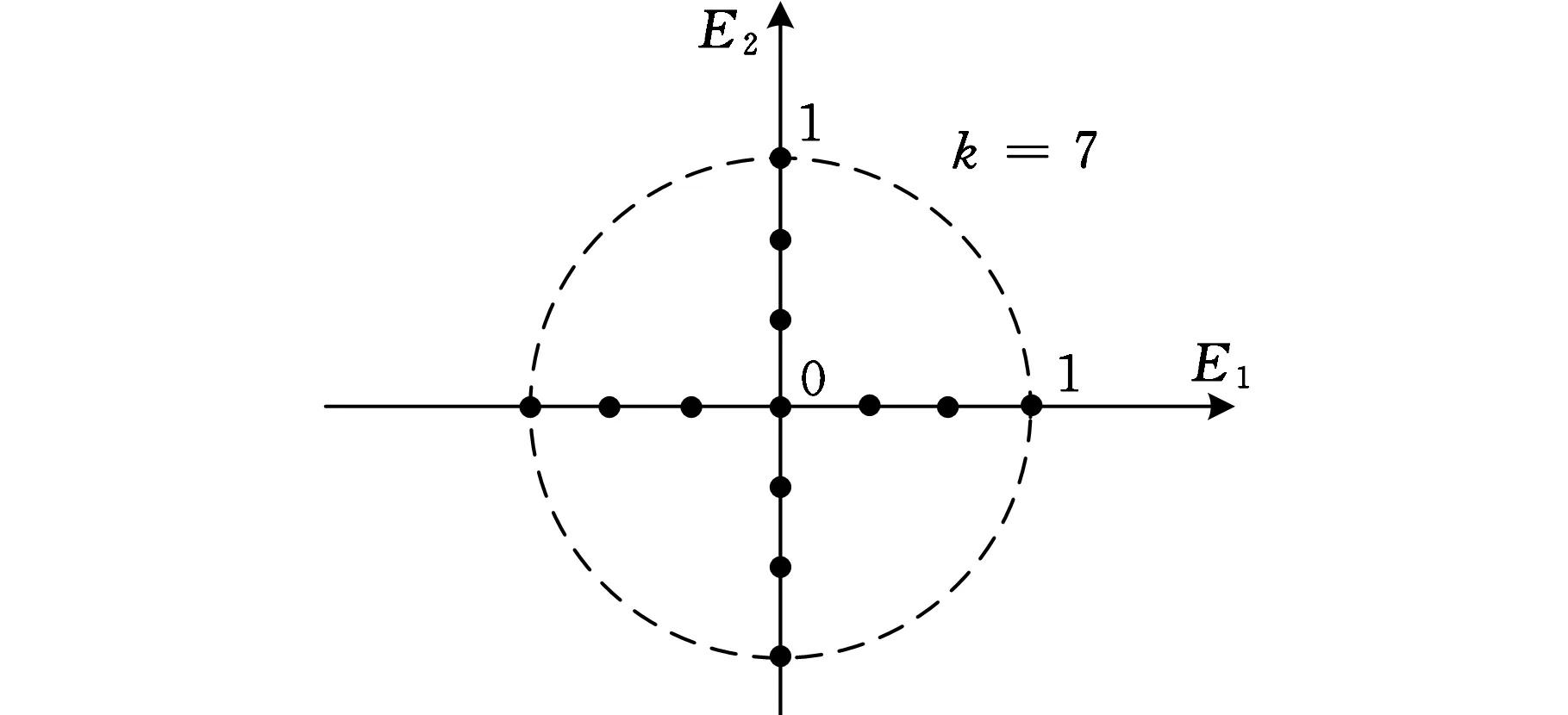
(b)区间变量的样本点分布图2　样本点分布示意图

将式(20)和式(21)代入式(14)～式(17)，可得失效概率的最小值和最大值的计算式分别为

pf，min=Pr{Gmax=(1-NX-NY)g(c)+

(22)

pf，max=Pr{Gmin=(1-NX-NY)g(c)+

(23)

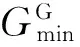
(24)

(25)

一旦最大概率点(MPP)和各个二次多项式系数确定，基于HDMR的混合型可靠性计算方法就无须再调用原始的状态极限函数。这可大幅度提高计算效率，尤其当极限状态函数以隐式的计算机仿真模型表述时，调用一次状态极限函数的用时一般较长。为高效求得最大概率点，已有学者提出了较多的数值算法，如HLRF法[19-20]、iHLRF法[21]等。作为HLRF法的改进，iHLRF法引入了价值函数，在处理非线性度较高的极限状态函数时仍具较好的收敛性，故被广泛应用。为此，采用iHLRF法求解最大概率点。

4　算例

在MATLAB下，编写了提出的单步可靠性算法可执行程序，计算了两个混合型可靠性分析算例，其中第一个算例的非线性较低，输入变量的维度较低，相比于第一个算例，第二个算例的非线性度较高，输入变量的维度也较高，用于验证提出的单步可靠性算法在处理较高非线性和高维度时的计算效率及精度。在算例中，使用调用原始极限状态函数的次数Nc评定计算效率。尽管两个算例的极限状态函数均以显式表达式给出，但都编写成了可执行程序，故对于调用函数，极限状态函数是隐式的。在用于求解最大概率的iHLRF算法中采用向前有限差分法计算极限状态函数关于随机变量的梯度。

4.1悬臂梁

某悬臂梁末端受外部载荷，其中，水平方向分量为Px，垂直方向分量为Py，如图3所示。当梁末端位移大于末端许用位移D0时，认为刚度失效，则极限状态函数为

其中，L为悬臂梁长度；b和h分别为矩形梁截面的宽度和高度；E为材料弹性模量。

图3　悬臂梁

已知，末端许用位移D0=65 mm。表1给出了各个随机变量的分布参数及区间变量的特征矩阵，其中，L、b和h均服从正态分布；弹性模量E为独立区间变量，载荷分量Px和Py为非独立区间变量。

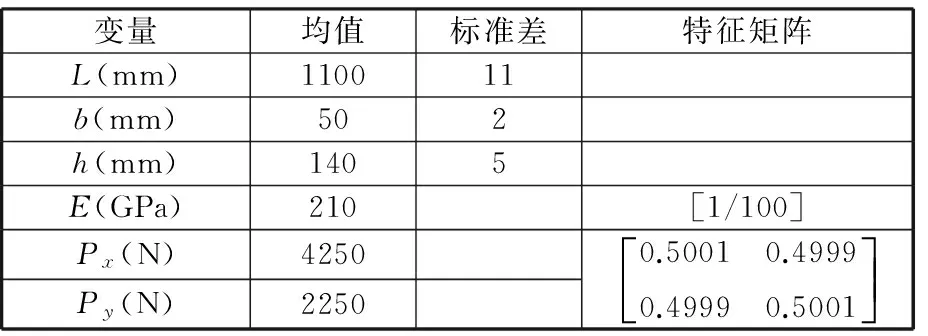
表1　不确定性变量的参数

为研究不同样本数量对计算结果精度的影响，在使用提出的可靠性计算方法计算失效概率时，令k值分别为5、7和9。表2给出了不同k值时的失效概率结果。为验证计算结果的精度，同时使用了蒙特卡罗法计算失效概率。因蒙特卡罗法仅能计算系统中不确定性都为随机变量的工况，故在使用蒙特卡罗法时，将各个区间变量在可行域内均布取样30个点，对满足多椭球模型约束条件的区间样本点，调用107次原始极限状态函数，计算失效概率，最后挑选出失效概率的最小值和最大值，作为失效概率的上下限。由表2可见，当k值等于9时，计算结果与蒙特卡罗法获得的结果较接近，具有较高的计算精度；根据Nc可知，提出的基于HDMR的单步可靠性计算方法可较少地调用原始极限状态函数，求得较高精度的失效概率上下限值。

表2　失效概率上下限

4.2悬臂圆筒

某悬臂圆筒受外部载荷如图4所示：集中力F1、F2，P和扭矩T。当最大等效von-Mises应力σmax超出材料屈服极限σs时，认为悬臂圆筒强度失效，极限状态函数可写为

G=g(X,Y)=σs-σmax

图4　悬臂圆筒

最大等效von-Mises应力位于悬臂圆筒根部截面上端点，其计算式为

其中，σx为该点处的正应力，表达式为

c=d/2

M=F1L1cosθ1+F2L2cosθ2

其中，M为该截面处弯矩，A为截面面积，I为截面惯性矩，τzx为该点的切应力。

表3给出了各个随机变量的分布参数及区间变量的特征矩阵，其中θ1和θ2为独立区间变量，其余不确定性变量均为随机变量。

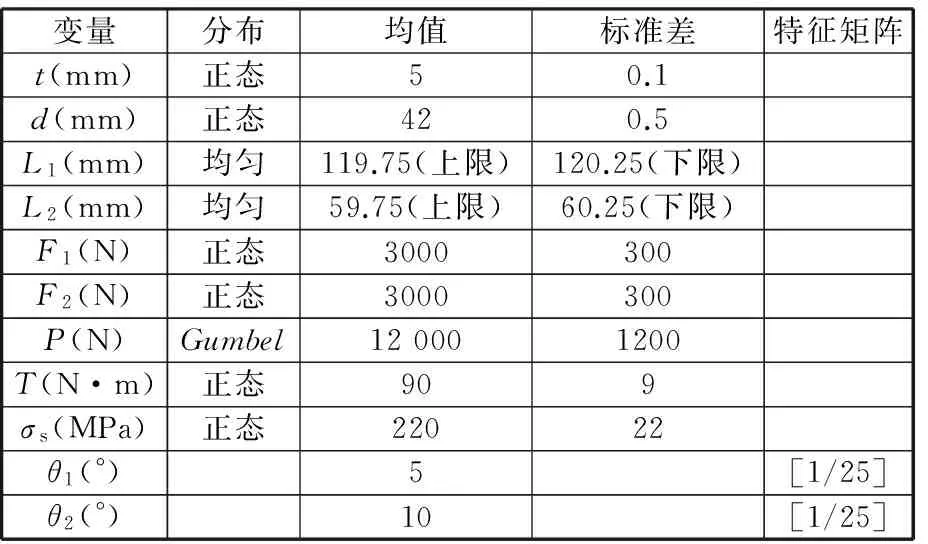
表3　随机变量分布参数

比较研究了k值对计算结果精度的影响，表4给出了基于提出的方法，令k值分别为5、7和9时的计算结果。为验证计算结果的正确性，在蒙特卡洛法中，将两个区间变量在可行域内均布取样50个点，对满足多椭球模型约束条件的区间样本点，调用106次原始极限状态函数，计算失效概率，最后挑选出失效概率的最小值和最大值，作为失效概率的上下限。由表4可见，k值对该算例的计算结果几乎没有影响，并在k值较小时，失效概率上下限已接近基于蒙特卡罗法获得的值；根据Nc可得提出的基于HDMR的单步可靠性计算方法计算效率高。

表4　失效概率上下限

5　结语

针对机械系统中随机变量和非独立区间变量共存的常见工况，基于椭球模型，利用HDMR法，提出了单步可靠性计算模型；使用多项式近似，提出了一种快速可靠性计算算法。由算例结果表明：该算法仅利用少量的原始极限状态函数的响应信息，或较少的调用次数，即可快速地计算获得较高精度的失效概率上下限。

在处理极限状态方程关于输入变量在可行区间内高度非线性情况时，基于二次多项式函数近似的高维模型的一阶分量函数可能会存在较大的误差，影响计算精度，提出多项式函数阶数自适应极限状态方程非线性的近似方法是一种可行的改进方法。

[1]NikolaidisE,GhiocelDM,SinghalS.EngineeringDesignReliabilityHandbook[M].NewYork:CRCPress, 2004.

[2]ElishakoffI.UncertaintiesinMechanicalStructures:AMFReudenthal’sCriticismsandModernConvexModels[J].JournalofAppliedMechanics, 1999, 63(1):683-692.

[3]WangP,YounBD,XiZ,etal.BayesianReliabilityAnalysiswithEvolving,Insufficient,andSubjectiveDataSets[J].JournalofMechanicalDesign, 2009, 131(11):111008.

[4]DuboisD,PradeH.ASyntheticViewofBeliefRevisionwithUncertainInputsintheFrameworkofPossibilityTheory[J].InternationalJournalofApproximateReasoning, 1997, 17(2):295-324.

[5]ShaferG.AMathematicalTheoryofEvidence[M].Princeton:PrincetonUniversityPress, 1976.

[6]Ben-HaimY,ElishakoffI.ConvexModelsofUncertaintyinAppliedMechanics[M].Amsterdam:Elsevier, 1990.

[7]DuX,SudjiantoA,HuangB.Reliability-basedDesignwiththeMixtureofRandomandIntervalVariables[J].JournalofMechanicalDesign, 2005, 127:1068-1076.

[8]江涛, 陈建军, 姜培刚,等. 区间模型非概率可靠性指标的一维优化算法[J]. 工程力学, 2007, 24(7):23-27.

JiangTao,ChenJianjun,JiangPeigang,etal.AOne-dimensionalOptimizationAlgorithmforNon-probabilisticReliabilityIndex[J].EngineeringMechanics, 2007, 24(7):23-27.

[9]DuX.UnifiedUncertaintyAnalysisbytheFirstOrderReliabilityMethod[J].JournalofMechanicalDesign, 2008, 130(9):091401.

[10]JiangC,HanX,LiuGP.ASequentialNonlinearIntervalNumberProgrammingMethodforUncertainStructures[J].ComputerMethodsinAppliedMechanicsandEngineering, 2008, 197(49/50):4250-4265.

[11]姜潮, 黄新萍, 韩旭,等. 含区间不确定性的结构时变可靠度分析方法[J]. 机械工程学报, 2013, 49(10):186-193.JiangChao,HuangXinping,HanXu,etal.Time-dependentStructuralReliabilityAnalysisMethodwithIntervalUncertainty[J].JournalofMechanicalEngineering, 2013, 49(10):186-193.

[12]DuX.Reliability-basedDesignOptimizationwithDependentIntervalVariables[J].InternationalJournalforNumericalMethodsinEngineering, 2012, 91(2):218-228.

[13]JiangC,ZhangZG,ZhangQF,etal.ANewNonlinearIntervalProgrammingMethodforUncertainProblemswithDependentIntervalVariables[J].EuropeanJournalofOperationalResearch, 2014, 238(1):245-253.

[14]JiangC,ZhengJ,NiBY,etal.AProbabilisticandIntervalHybridReliabilityAnalysisMethodforStructureswithCorrelatedUncertainParameters[J].InternationalJournalofComputationalMethods, 2015, 12(4)：No.4.

[15]姜潮, 郑静, 韩旭,等. 一种考虑相关性的概率-区间混合不确定模型及结构可靠性分析[J]. 力学学报, 2014, 46(4):591-600.JiangChao,ZhengJing,HanXu,etal.AProbabilityandIntervalHybridStructuralReliabilityAnalysisMethodConsideringParameters’Correlation[J].EngineeringMechanics, 2014, 46(4):591-600.

[16]RabitzH,AliF,ShorterJ,etal.EfficientInput-outputModelRepresentations[J].ComputerPhysicsCommunications, 1999, 117(1/2):11-20.

[17]Ben-HaimY.ConvexModelsofUncertainty:ApplicationsandImplications[J].Erkenntnis, 1994, 41(2):139-156.

[18]LiG,RosenthalC,RabitzH.HighDimensionalModelRepresentations[J].TheJournalofPhysicalChemistryA, 2001, 105(33):7765-7777.

[19]HasoferAM,LindNC.ExactandInvariantSecond-momentCodeFormat[J].JournaloftheEngineeringMechanicsDivision, 1974, 100(1):111-121.

[20]RackwitzR,FlesslerB.StructuralReliabilityUnderCombinedRandomLoadSequences[J].Computers&Structures, 1978, 9(5):489-494.

[21]ZhangY,KiureghianA.TwoImprovedAlgorithmsforReliabilityAnalysis[C]//Proceedingsofthe6thIFIPWG7.5WorkingConferenceonReliabilityandOptimizationofStructuralSystems.US:Springer, 1995:297-304.

(编辑王艳丽)

An One-step Reliability Analysis Method with Random and Dependent Interval Variables

Pan BaisongXie ShaojunJiang Lizheng

Zhejiang University of Technology,Hangzhou,310014

Random variables and dependent interval variables often coexisted, and this made the reliability analysis problem into a double-loop optimization problem and reduces the efficiency of the reliability analysis. So an one-step reliability analysis method was proposed. Specifically, the double-loop optimization problem where the dependent interval variables were modelled by the ellipsoid model, was decoupled into a simple one-step problem by using the HDMR. Based on the proposed sampling strategy, a quadratic polynomial was applied to approximate each of the HDMR expression, making the implicit one-step problem into the explicit one. The example results show that the proposed method has good efficiency and accuracy, and may calculate the reliability results with good accuracy at a little cost of calling the origin limit-state function.

ellipsoid model; dependent interval variable; high dimensional model representation(HDMR); rapid reliability analysis method

2015-09-21

国家自然科学基金资助项目(51475425,51075365)

TH122

10.3969/j.issn.1004-132X.2016.18.003

潘柏松(通信作者)，男，1968年生。浙江工业大学机械工程学院教授、博士研究生导师。主要研究方向为可靠性设计、可靠性工程、现代设计方法。出版专著1部，发表论文40余篇。谢少军，男，1986年生。浙江工业大学机械工程学院博士研究生。蒋立正，男，1979年生。浙江工业大学机械工程学院博士研究生。