杨永良，孔德宏

(昆明市第十六中学，云南 昆明 650200；云南师范大学数学学院，云南 昆明 650092)



几何画板条件下椭圆的25种典型作法*

杨永良，孔德宏

(昆明市第十六中学，云南 昆明 650200；云南师范大学数学学院，云南 昆明 650092)

用几何画板探究椭圆的不同作法，能够激发学生学习椭圆的兴趣，加深对椭圆相关数学知识的理解，提高几何画板的使用水平.本文借助几何画板，给出了椭圆的25种作法，并指出了其数学原理，或给出了数学证明。

几何画板；椭圆；作法；证明

椭圆是我们所熟悉的一种重要而又优美的曲线，它的作法很多，其中最简单最优美的作法就是根据椭圆第一定义的手工作法，即：取一条定长细绳，把它的两端分别固定在画图板上的F1和F2点，当绳长大于F1和F2的距离时，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动，就可以画出一个椭圆.然而在数学教师都喜闻乐见的几何画板软件中，我们却不可能直接像手工做法那样去作出一个椭圆，因为几何画板软件有自己的一套操作和制作规则.这似乎给我们带来了极大的麻烦和困难，然而另一方面，充分挖掘几何画板的强大功能，也会给我们带来许多意想不到的惊喜！例如，可以间接地作出本例的椭圆.

于是我们就会产生这样的想法：满足什么条件的动点，其轨迹会是椭圆？我们希望这个动点要容易作出来，进而，其轨迹──椭圆也就容易构造出来了.特别地，我们要在技术的支撑下进行探究，这是一个极富于挑战，又充满乐趣的开放性的研究性课题.需要指出的是，它不仅取决于我们的知识，而且还取决于我们的方法和手段.下面将重点讨论：在几何画板技术的条件下，椭圆有哪些不同的典型作法？

用几何画板探究椭圆的不同作法，能够激发学生学习椭圆的兴趣，加深对椭圆相关数学知识的理解，同时提高几何画板的使用水平. 下面将从八个方面：一、平面几何法(椭圆的第一定义、第二定义等)；二、代数法(普通方程、参数方程、极坐标方程)；三、交轨法；四、变换法；五、包络法(需要用到高等数学的知识)；六、物理法(凸透镜法)；七、立体几何法(用平面截圆锥)；八、其他方法，给出几何画板条件下椭圆的25种典型作法，同时也给出了必要的说明或数学证明.需要指出的是，每一种作法都对应一定的数学知识，读者务必搞清数学原理，同时结合几何画板的使用方法，这样才能明白每种做法的依据和来龙去脉.

一、根据椭圆的定义作椭圆

方法1：交弧法

作法：如图1.

1.作AB=2a，在线段AB取一动点P.

2.作两个点F1和F2，以F1为圆心，AP为半径作圆C1；以F2为圆心，BP为半径作圆C2.

3.记圆C1和圆C2的交点为M(注意有两个交点，否则就只能得到半个椭圆)，以P为主动点，M为从动点构造轨迹便得到椭圆.

方法2：单圆法(1)[1]

作法：如图2.

1.作AB=2a.以F1为圆心，以线段AB为半径作圆.

2.在圆上取动点P.记线段PF2的中垂线与线段F1P的交点为M，以P为主动点，M为从动点构造轨迹便得到椭圆.

∴动点M的轨迹为以F1、F2为焦点的椭圆.

方法3：椭圆的第二定义[2]

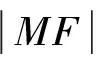
作法：如图3.

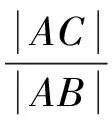
3.以F为圆心，OP为半径作圆；

4.按标记的距离平移准线L，平移后的准线与圆相交于M(注意有两个交点，否则就只能得到半个椭圆)，以P为主动点，M为从动点构造轨迹便得到椭圆.

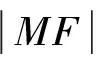
二、代数方法(用椭圆的方程)

方法4：直接建立参数，根据普通方程，画函数图像.

作法：如图4.

1.作参数a=3，b=1.

(按数字键盘上的+、-号，可以改变参数a,b的值，椭圆曲线会随之发生相应的变化.只需a≠b，且a≠0、b≠0即表示椭圆.值得注意的是，即便a、b取负值也表示椭圆.)

方法5：以线段的长作为参数，根据普通方程，画函数图像.

作法：如图5.

1.分别在X轴、Y轴上作点A、点B.分别以线段OA、OB的长作为参数a、b.

(拖动点A或者点B，可以改变参数a,b的值，椭圆曲线会随之发生相应的变化.方法5与方法4相较而言，参数具有直观的几何意义，有利于学生形象思维的发展.)

方法6：根据普通方程，描点作出函数图像.

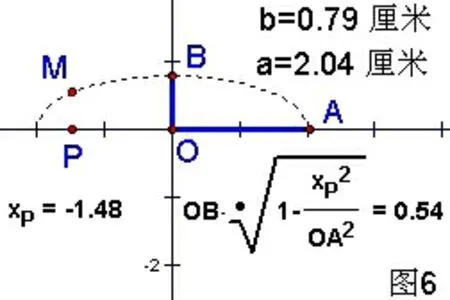
作法：如图6.

1.分别在X轴、Y轴上作点A、点B.以线段OA、OB的长作为参数a、b.

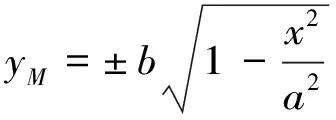
4.选主动点P和从动点M，构造轨迹，可以分别得出上半椭圆和下半椭圆.

(拖动点A或者点B，可以改变参数a,b的值，椭圆曲线会随之发生相应的变化.方法6说明了这样一个事实：在技术的支持下，以往受到冷落的描点作函数图像的方法现在又重新得到了人们的重视.)

方法7：直角坐标下的参数方程(同心圆法)[2]

作法：如图7.

1.以O为圆心，分别以OA、OB为半径作两个圆.

2.在大圆上任取一点P，连接OP交小圆于点C.

3.过P作X轴的垂线，过C作X轴的平行线，两直线相交于点M.

4.选主动点P和从动点M，构造轨迹，得到椭圆.

分析：设OA=a，OB=b，∠POA=θ，

∵M点、P点的横坐标相同，M点、C点的纵坐标相同，而P点的横坐标为acosθ，C点的纵坐标为bsinθ，

∴M(acosθ，bsinθ)，即M点的轨迹为椭圆.

方法8：直角坐标下的参数方程(同心圆法)

作法：如图8

1.以O为圆心，分别以OA、OB为半径作两个圆.设OA=a，OB=b.

2.在大圆上任取一点P，设∠POA=θ.分别计算acosθ，bsinθ，-bsinθ.

3.绘制点M(acosθ，±bsinθ)，由于几何画板里的0θ180°，故纵坐标要取两个：±bsinθ，否则只能得到上半椭圆.

4.选主动点P和从动点M，构造轨迹，得到椭圆.

方法9：直角坐标下的参数方程(同心圆法)

作法：如图9

5.以O为圆心，分别以OA、OB为半径作两个圆.设OA=a，OB=b

6.在大圆上任取一点P，设∠POA=θ.分别计算asinθ，-asinθ，bcosθ.

7.绘制点M(±asinθ，bcosθ)，由于几何画板里的0θ180°，故横坐标要取两个：±acosθ，否则只能得到右半椭圆.

8.选主动点P和从动点M，构造轨迹，得到椭圆.

(方法8与方法9的差异在于参数方程的不同.)

方法10：根据极坐标方程.

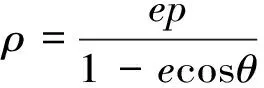
作法：如图10.

1.直接建立参数e、p，例如e=0.8，p=1.

(按数字键盘上的+、-号，可以改变参数e、p的值，椭圆曲线会随之发生相应的变化)

方法11：根据极坐标方程.

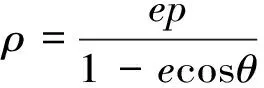
作法：如图11.

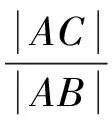
2.作一条线段，度量其长度作为p.

(拖动点C可以改变e的值，改变线段p的长度可以改变p值，椭圆曲线会随之发生相应的变化.方法11与方法10相较而言，其参数具有直观的几何意义.)

三、用轨迹的方法

方法12：两直线交点的轨迹(单圆法(2)).

原理：两直线交点的轨迹是椭圆

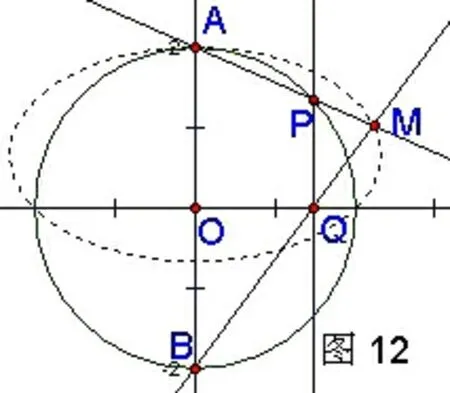
作法：如图12.

1.设圆O与y轴交于A、B点，在圆O上任取一点P.

2.过P作X轴的垂线，交X轴于Q点.

3.设直线AP与BQ相交于M点.

4.选主动点P和从动点M，构造轨迹，得到椭圆.

则A(0,r)，B(0,-r)，Q(x′,0)，M(x,y)，

点M也满足这两条直线方程，又点P在圆上，即x′2+y′2=r2，消去参数x′、y′，

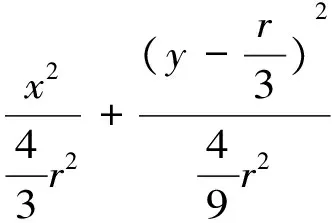
方法13：两直线交点的轨迹(切线法).

原理：两直线交点的轨迹是椭圆

作法：如图13.

1.设圆O与x轴交于A、B点，过A、B分别作圆O的切线.

2.在圆O上任取一点P，过P作圆O的切线分别与上述两条切线相交于点C、D.

3.设直线AD与BC相交于M点.

4.选主动点P和从动点M，构造轨迹，得到椭圆.

则A(-r,0)，B(r,0)，

于是过P的切线方程为x′x+y′y=r2，

点M也满足这两条直线方程.又点P在圆上，即x′2+y′2=r2，消去参数x′、y′，

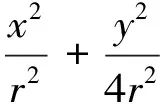
方法14：动点的轨迹(椭圆规).

原理：动点的轨迹是椭圆

作法：如图14.

1.在圆O上任取一点P，过P分别作X、Y轴的垂线，垂足分别是A、B.

2.在直线AB上任取一点M(除点A、B外).

3.选主动点P和从动点M，构造轨迹，得到椭圆.

说明：其实这就是教材中出现过的椭圆规，即：定长线段AB的两个端点A、B在坐标轴上滑动，直线AB上任一点M(除点A、B外)的轨迹为椭圆.

方法15：动点的轨迹.

原理：动点的轨迹是椭圆

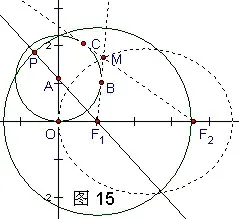
作法：如图15.

1.在X轴正半轴上取两个定点(焦点)F1和F2，以F1为圆心作一个圆F1，在圆上任取点P.

2.直线PF1交Y轴于A点，以A为圆心，过原点O作圆A.

3.过F1作圆A的(异于X轴)切线F1B.

4.过F2作圆A的(异于X轴)切线F2C.

5.两切线F1B、F2C交于点M.

6.选主动点P和从动点M，构造轨迹，得到椭圆.

证明：由圆的切线性质知：MF1+MF2=(MB+BF1)+MF2

=(MC+OF1)+MF2

=OF1+(MC+MF2)

=OF1+CF2

=OF1+OF2(定值)

∴动点M的轨迹为椭圆.

四、伸缩法

方法16：动点的轨迹.

原理：沿某一方向，圆经过压缩或伸长得到椭圆.

作法：如图16

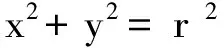
2.取圆上一动点P，连PB，交x轴于点A.

3.在y轴上任取一点C，连AC，交过P且平行于y轴的直线于M点.

4.选主动点P和从动点M，构造轨迹，得到椭圆.

5.(拖动点C，可改变椭圆的形状和大小).

证明：设P(x′,y′)，M(x,y)，则x=x′.

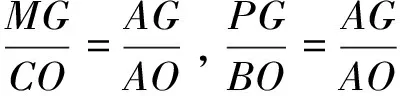
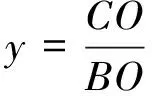
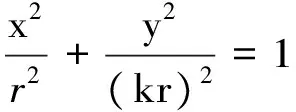
∴动点M的轨迹为椭圆，其在x轴上的半轴长为r，在Y轴上的半轴长为kr.

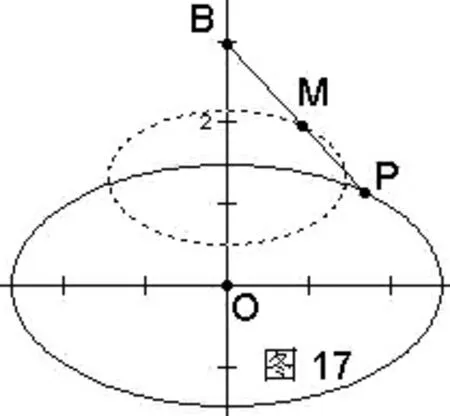
方法17：椭圆的相似

作法：如图17

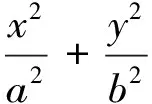
2.在平面内任取一点B，在线段BP上任作一点M.

3.选主动点P和从动点M，构造轨迹，得到椭圆.

(拖动点M，可改变椭圆的大小).

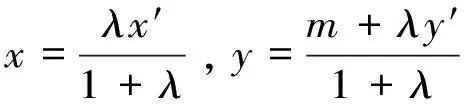
∴动点M的轨迹为椭圆.

五、包络法

方法18：圆族的外包络

作法：如图18

1.以原点O为圆心任作一圆O.

2.在X轴上任取一点A，过A作Y轴的平行线交圆O于B点.

3.以A为圆心，过点B作圆A.

4.选主动点A和从动(点)圆A，构造轨迹，则圆A的外包络为一个椭圆.

消去c而得到的曲线之中.

∴圆A方程为(x-c)2+y2=r2-c2.其关于c的导数方程为-2(x-c)+2c=0，

方法19：切线族的包络

作法：如图19

1.作一圆O，在圆O内取不同于圆心的一点F.

2.在圆O上取一动点P，作线段PF的中垂线L.

3.选主动点P和从动(点)线L，构造轨迹，则切线族的包络为一个椭圆.

方法20：弦线族的包络

作法：如图20

1.作一圆O，在圆O内取不同于圆心的一点F.

2.在圆O上取一动点P，直线PF交圆O于点A.

3.直线AO交圆O于点B.

4.连接直线BP.

5.选主动点P和从动(点)线BP，构造轨迹，则弦线族的包络为一个椭圆.

六、其他方法

方法21：通过凸透镜成像把圆成像成圆锥曲线

作法：如图21

1.在凸透镜的左侧任意作一个圆.

2.在圆上取一动点P，点P通过凸透镜的成像点为P'.

3.选主动点P和从动点P'，构造轨迹，则P'的轨迹为一个椭圆.

方法22：椭圆的斜二测画法

作法：如图22

1.作一圆O，在圆O上取任一点P.

2.过P作X轴的垂线，垂足为N.

3.以N为旋转中心，P点顺时针旋转45°得到P'点.

5.选主动点P和从动点M，构造轨迹，则得到一个椭圆.

方法23：椭圆按标记角的“斜二测”画法

作法：如图23

1.新建角度参数t，如图t=-62°.

2.作一圆O，在圆O上取任意点P.

3.过P作X轴的垂线，垂足为N.

4.以N为旋转中心，P点旋转角度t，得到P'点.

6.选主动点P和从动点M，构造轨迹，则得到一个椭圆.

方法24：用平面截圆锥[2]

作法：如图24

1.作椭圆，使其中心在原点，长轴AB在X轴上.

2.在Y轴上取一点S，在椭圆上取一点C，连接SC，选择主动点C和从动线(点)SC，构造轨迹，得圆锥SC.

3.在线段SO上取一点E，过E作EF∥X轴交SB于点F.过E作直线n∥CO.

4.作圆H，在其上任取一点I.

5.过F作FG∥HI交直线n于点G.

6.在线段SO上取一点D，直线DG交SC于点M.

7.选择主动点C和从动点M，构造轨迹，得椭圆.

(拖动点E、点D、点I可以改变截面的高度和倾斜度.)

方法25 直接绘制参数曲线

作法：如图25(这是新版几何画板5.06的功能)

1.新建参数a，新建函数f(x)=acosx.

2.新建参数b，新建函数g(x)=bsinx.

3.先后选中函数f(x)=acosx、g(x)=bsinx，绘图—>绘制参数曲线，让定义域t包含(0,π)，即可绘制出椭圆.

[1]缪亮，盘俊春.几何画板5.X课件制作实用教程[M].北京：清华大学出版社，2012.

[2]陶维林.几何画板实用范例教程(第3版)[M].北京：清华大学出版社，2013.

(责任编辑 李艳梅)

25 Kinds of Typical Ellipse Construction under the Condition of the Geometer's Sketchpad

YANG Yongliang & KONG Dehong

(KunmingNO. 16MiddleSchool,Kunming, 650200,YunnanProvince;SchoolofMathematics,YunnanNormalUniversity,Kunming, 650092,YunnanProvince)

Inquiring different ways of making ellipses by using the Geometer's Sketchpad can motivate students’ learning about ellipses, and also enhance their mathematical knowledge about ellipses, improve the effective use of the Geometer's Sketchpad. This article proposes 25 ways of construction ellipses based on the use of the Geometer's Sketchpad, mathematical principles and proof are offered as well.

The Geometer's Sketchpad, ellipse, construction, proof

2016 - 05 - 07通讯作者：孔德宏(1972—)，男，副教授，主要从事数学教育与数学教育技术研究

O123.5

A

1671 - 7406(2016)06 - 0005 - 10