夏新涛，朱文换，孙立明，叶亮，邱明

(1. 河南科技大学 机电工程学院，河南 洛阳 471003；2. 洛阳轴研科技股份有限公司，河南 洛阳 471039)

为确保安全运行，试验机、飞机、高铁、汽车等机械系统对滚动轴承试验或服役时期的可靠性要求越来越高[1]。在轴承试验或服役过程中，由于诸多原因造成滚动轴承的性能指标达不到使用要求，使其产生疲劳、磨损、烧伤等失效，甚至发生恶性事故。因此，在轴承试验或服役期间滚动轴承无失效时或者没有发现失效时，应事先分析滚动轴承的无失效数据[2]，对滚动轴承的失效概率进行估计[3-6,13]，即根据滚动轴承的无失效数据对滚动轴承的可靠性进行预测。

目前，无失效数据可靠性评估采用的研究方法主要有经典统计学法和Bayes统计法，最常用的是Bayes统计法[2-10]，其前提是已知所研究滚动轴承寿命的概率分布，如对数正态分布[3]、指数分布[6]、Weibull分布[5,8-9]、二项分布、均匀分布等。而滚动轴承的多种失效导致了其概率分布未知，因此，现有方法对概率分布未知的滚动轴承寿命无失效数据可靠性的研究有一定的缺陷。

现融合自助法[11]和最大熵原理[12]，运用自助最大熵法，首先处理滚动轴承寿命试验或服役过程中概率分布已知和未知时的无失效数据，然后构建寿命失效数据的可靠性函数，进而预测寿命失效数据可靠性的真值函数及其上下界函数，实现滚动轴承寿命无失效数据可靠性评估。

需要说明的是，提出的自助最大熵法是针对滚动轴承试验或服役期间没有发生任何失效时获取的无失效数据，即所考察的无失效数据不同于定时截尾试验中获得的无失效数据。因此，自助最大熵法不适用于定时截尾试验轴承均无失效的相同无失效数据的分析,定时截尾试验中轴承均无失效时的情况需要进一步研究。

1 建立无失效数据可靠性模型

1.1 数据采集

假设滚动轴承无失效数据为随机变量x，对其寿命无失效数据进行定期采样，获取原始数据，构成一个无失效数据序列X,

X=(x(1),x(2),…,x(n));

n=1,2,…,N，

(1)

式中：x(n)为第n个无失效数据；n为无失效数据的序号；N为无失效数据的个数。

1.2 数据生成

根据自助原理，通过自助再抽样将原始无失效数据生成大量无失效数据。在进行自助抽样前，需选定抽样个数。首先令第1组选取的抽样个数为L1，然后等间隔地选择抽样个数Li(i为抽样个数的组号，一般取4～10)，直到Li=N为止；然后对抽样个数不同的多组原始无失效数据分别进行自助再抽样，根据自助原理从X中等概率可放回地进行抽样，抽取n次，可得到一个自助样本Xib，且其共有N个数据。连续重复抽取B次，得到B个自助再抽样样本，即大量无失效数据XB为

XB=(Xi1,Xi2,…Xib,…XiB);b=1,2,…,B,

(2)

Xib=(xib(1),xib(2),…,xib(n));

n=1,2,…，N,

式中：Xib为第i组自助样本Xi的第b个自助样本；B为第i组自助样本XB的数据个数，一般取1 000～100 000；xib(n)表示自助样本Xib中的第n个数据。

自助样本Xib的均值为

(3)

1.3 预测数据的概率分布

根据最大熵原理，原始无失效数据生成的大量无失效数据应满足最大熵准则。用最大熵法可以获取大量无失效数据的概率分布的最好估计。

对于原始无失效数据生成的大量无失效数据，用一连续变量u来表示大量无失效数据序列XB中的自助样本Xib，定义最大熵H(u)为

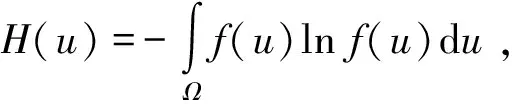
(4)

式中：f(u)为无失效数据的概率密度函数；Ω为变量u的积分区间。

(4) 式的约束条件为

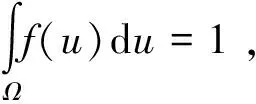
(5)

(6)

式中：m为所用原点矩的阶数；mk为第k阶原点矩。

根据 (2) 式可得无失效数据的各阶原点矩为

(7)

令

H(u)→max ，

(8)

(9)

令

(10)

可得到

(11)

(12)

(13)

(14)

(14) 式为最大熵概率密度函数的解析式。

将(14)式代入 (5) 式可得

(15)

求解可得

(16)

(17)

将 (16) 、(17)式分别对λk进行微分可得

(18)

(19)

比较(18)式和(19)式，m阶原点矩应满足

(20)

通过(20)式可建立求解λ1,…,λk,…,λm的m个方程组，再由(18)式求出λ0，可得无失效数据的概率密度函数f(u)的解析式。

由f(u)解析式可得无失效数据的概率分布函数F(u)为

(21)

1.4 构建可靠性函数

定义一个有关滚动轴承寿命无失效数据个数的估计参数G(u)为

G(u)=N[1-F(u)]。

(22)

假设有关滚动轴承寿命的经验失效概率分布函数P(u)为

(23)

式中：c为经验概率系数，其取值会影响可靠性函数的计算结果。

当c为0.01～0.5时，c越小，可靠性函数的取值范围越小；反之，可靠性函数的取值范围越大[13]。在滚动轴承寿命试验或服役过程中，假设无失效数据的取值区间是[xmin,xmax]=[x(1),x(N)]。根据现有的可靠性研究成果和工程实践[7,13-14]，当寿命x的取值接近xmin时，失效数据的可靠性高；当寿命x的取值接近xmax时，失效数据的可靠性低。在x=xmax之前，滚动轴承寿命试验或服役过程中没有出现失效，即仅获得了无失效数据；在x=xmax时，失效数据的估计可靠性函数的可信度通常为85%～95%[7,13-14]，对应的c值约为0.1。

根据可靠性理论，预测滚动轴承寿命失效数据的可靠性函数r(u)为

根据(24)式及生成的多组大量无失效数据，可预测出滚动轴承寿命失效数据的多组可靠性函数。

1.5 预测真值函数及其上下界函数

设有S个失效数据，分别获取同一失效数据所对应的多组可靠性函数的取值，将其构成一个滚动轴承寿命失效数据的可靠性数据序列R

R=(R1,R2,…,Rs);s=1,2,…,S，

(25)

Rs=(rs(1),rs(2),…,rs(j),…,rs(i));

j=1,2,…,i，

式中：s为失效数据可靠性数据序列的序号；Rs为第s个失效数据的可靠性数据序列；j为寿命失效数据的可靠性数据的序号；rs(j)为Rs中的第j个数据。

根据自助原理，从失效数据的可靠性数据序列Rs中等概率可放回地进行抽样，抽取i次，可得到一个自助样本Rsb，且其共有i个数据。连续重复抽取B次，得到B个自助再抽样样本，即失效数据的大量可靠性数据序列RB为

RB=(Rs1,Rs2,…,Rsb);b=1,2,…,B，

(26)

式中：Rsb为RB的第b个自助样本。

运用最大熵原理，对于由 (26) 式模拟出的B个RB，用一连续变量z来表示失效数据的可靠性数据的自助样本Rsb，根据 (4)～(20) 式，可得寿命失效数据可靠性的概率密度函数φ为

φ=φ(z) 。

(27)

预测滚动轴承寿命失效数据可靠性的真值函数RT为

(28)

假设显著性水平α∈[0,1]，置信水平P为

P=1-α，

(29)

对应置信水平P=α/2处的置信区间的下边界函数RL=Rα/2，且满足

(30)

对应置信水平P=1-α/2处的置信区间的上边界函数RU=R1-α/2，且满足

(31)

因此，在置信水平P下，滚动轴承寿命失效数据可靠性的上界函数和下界函数可以用失效数据可靠性的取值区域D表示

D={RL,RU}={Rα/2,R1-α/2}。

(32)

2 研究案例

2.1 已知分布无失效数据

某滚动轴承的无失效数据见表1，共有6组11个数据。根据现有的可靠性研究[4]，认为滚动轴承寿命服从Weibull分布。

表1 滚动轴承的无失效数据

由表1可得滚动轴承的无失效数据序列X11(N=11)，如图1所示。

图1 滚动轴承的无失效数据序列X11

将这11个滚动轴承的无失效数据通过选择抽样个数进行分组:抽样个数L1=5，L2=7，L3=8，L4=11，共4组自助抽样。

设置信水平P=95%，根据自助最大熵法，分别对这4种情况的无失效数据建立失效数据的可靠性模型。

由自助最大熵法可得，理论上B的取值越大，预测的结果就越准确。在实际的案例分析中，当B取值过大时，会导致生成大量数据所用的时间过长；当B取值大到一定程度时，预测结果不再发生变化。因此，结合实际研究情况，在确保快速获取最佳预测结果的前提下，优选B=30 000。

在建立失效数据的可靠性模型时，令B=30 000，c=0.1，进而可预测出4组滚动轴承寿命失效数据的可靠性函数，如图2所示。

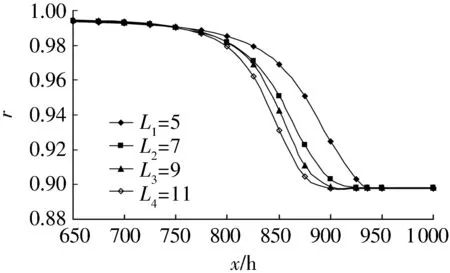
图2 4组滚动轴承寿命失效数据的可靠性函数

由图2可知，由于样本的抽样个数不同，获得的每组有关滚动轴承失效数据的可靠性函数的具体变化有一定差别，但总体上来看，随着滚动轴承试验或服役时间的不断增加，其寿命的可靠性均呈下降趋势。该趋势符合滚动轴承寿命在轴承试验或服役过程中逐渐衰减的实际规律。

基于滚动轴承寿命同一失效数据对应的可靠性数据序列，运用自助最大熵法，令B=30 000，可得滚动轴承寿命失效数据的可靠性真值函数及其上下界函数，如图3所示。图中还给出了运用现有方法(多层Bayes估计法)对该滚动轴承无失效数据可靠性的分析结果[4]。

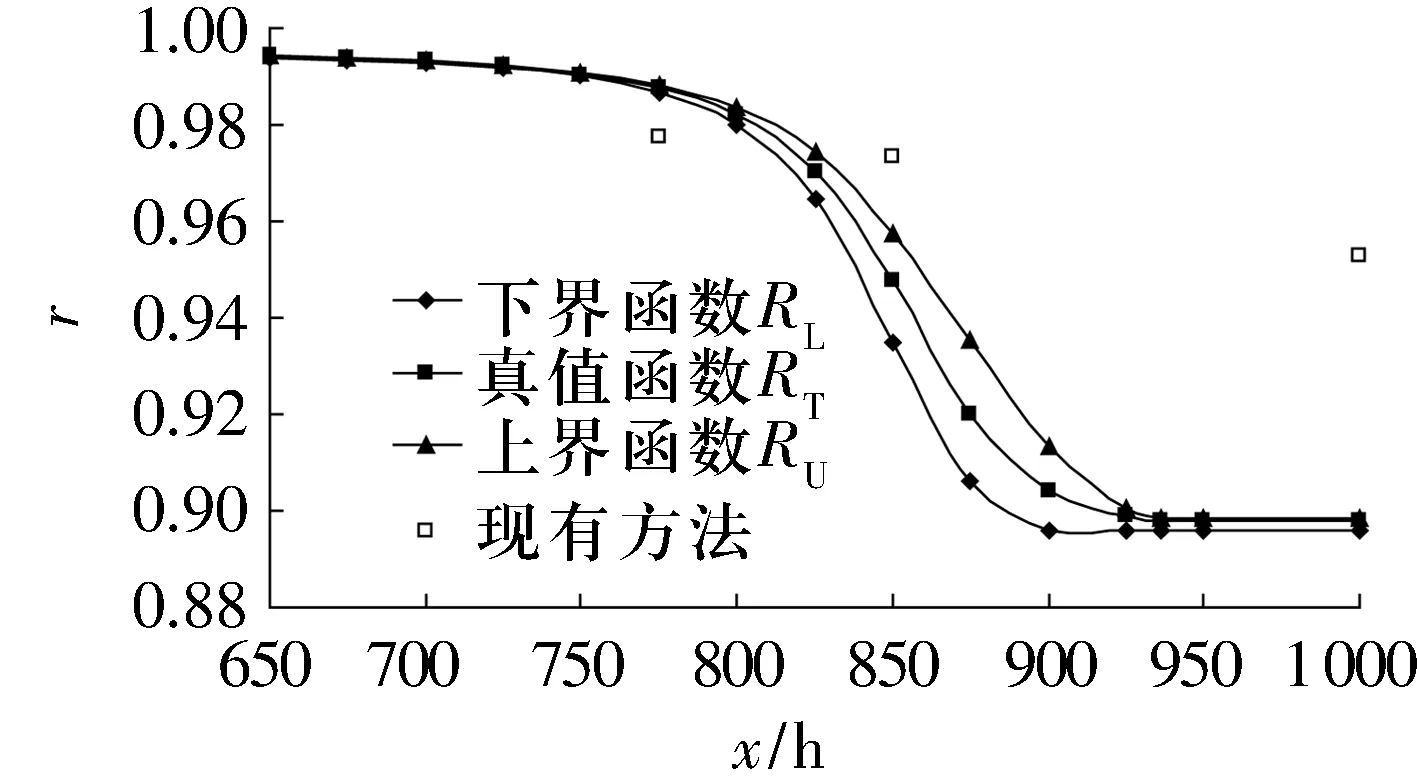
图3 滚动轴承寿命失效数据可靠性的真值函数及其上下界函数

由图3可知，当x=1 000 h时，由这2种方法得到的结果之间的差异最大。设x=1 000 h，用自助最大熵法预测的滚动轴承寿命失效数据可靠性估计真值RT(1 000)=89.82%。根据多层Bayes估计法，在滚动轴承寿命概率分布已知的条件下，假设滚动轴承寿命失效数据服从Weibull分布，当x=1 000 h时，计算的滚动轴承寿命失效数据可靠性为95.27%。二者最大差值为5.45%，相差很小，说明用自助最大熵法对滚动轴承寿命无失效数据的可靠性进行评估是可行的。

2.2 未知分布无失效数据

因滚动轴承寿命无失效数据来源于其运行时间，拟定一组数据作为寿命无失效数据，构成模拟无失效数据序列X10(N=10)，如图4所示。由于模拟无失效数据是主观拟定的，其概率分布是未知的。

图4 模拟的无失效数据序列X10

将这10个模拟无失效数据通过选择抽样个数进行分组：抽样个数L1=4，L2=6，L3=8，L4=10，共4组自助抽样。

设置信水平P=95%，根据自助最大熵法，分别对这4种情况的无失效数据建立失效数据的可靠性模型。同理，令B=30 000，c=0.1，则可预测4组模拟失效数据的可靠性函数，如图5所示。

图5 4组模拟失效数据的可靠性函数

由图5可知，由于样本的抽样个数不同，获得的每组模拟的失效数据可靠性函数虽有一定差别，但总随着模拟失效数据的不断增大，滚动轴承寿命的可靠性整体呈下降趋势。该趋势符合滚动轴承寿命随着时间推移逐渐衰减的实际规律。

基于同一模拟失效数据对应的可靠性数据序列，运用自助最大熵法，令B=30 000，可得模拟失效数据的可靠性真值函数及其上下界函数，如图6所示。

由图6可知，在模拟失效数据x取值范围内，模拟失效数据可靠性的真值函数及其上下界函数均呈递减趋势，则预测的模拟失效数据可靠性的真值函数及其上下界函数符合滚动轴承可靠性逐渐衰减的实际情况，说明用自助最大熵法在概率分布未知条件下评估滚动轴承寿命无失效数据的可靠性是可行的。

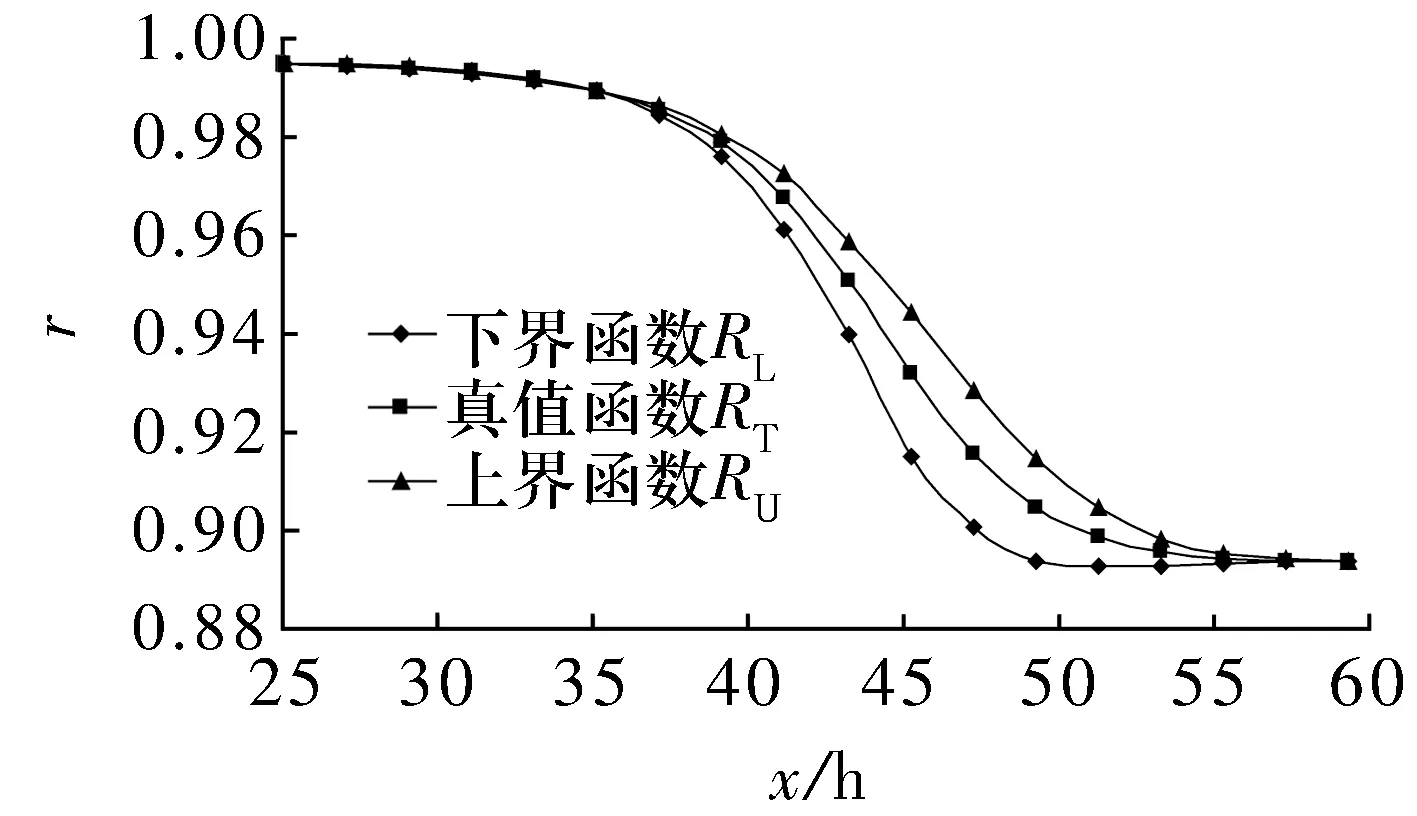
图6 模拟失效数据可靠性的真值函数及其上下界函数

2.3 讨论

已知分布无失效数据的实际案例为服从Weibull分布的寿命无失效数据可靠性评估案例,在概率分布已知的情况下，用自助最大熵法预测的寿命失效数据可靠性真值与现有方法得到的寿命失效数据可靠性取值相差很小，说明运用自助最大熵法可以较准确地预测寿命无失效数据的可靠性真值函数，该方法对于滚动轴承无失效数据的可靠性评估是可行的。另外，用自助最大熵法还可以预测出寿命无失效数据的可靠性上下界函数，而用现有方法是无法计算的。因此，在现有方法的可靠性研究中，可将自助最大熵法得到的寿命无失效数据可靠性上下界函数作为参考。

仿真试验为概率分布未知的寿命无失效数据可靠性评估案例，由试验结果可知，在概率分布未知的情况下，用自助最大熵法可以得到寿命失效数据可靠性的真值函数及其上下界函数。对比图6和图3可知，概率分布未知时预测的寿命失效数据可靠性真值函数及其上下界函数的变化规律与概率分布已知时预测的结果大致相同，说明自助最大熵法能够解决在概率分布未知条件下对无失效数据的可靠性进行评估这一难题。而对于概率分布未知的情况，现有方法是行不通的。

3 结束语

在概率分布已知和未知的情况下，用自助最大熵法预测滚动轴承寿命的失效数据，经实际案例和仿真试验证明，该方法对寿命的概率分布没有要求，可以实现寿命无失效数据的可靠性评估。对于相同的一组无失效数据，运用现有方法和自助最大熵法获得的可靠性结果是相同的，而实际工程上该结果有可能不同，在未来工作中有待深入研究。