林惠贤

(广东省佛山市南海区大沥镇高级中学,528231)

○解题研究○

一道数列高考题的解题研究

林惠贤

(广东省佛山市南海区大沥镇高级中学,528231)

数列是高中数学的重点内容之一,也是与大学数学衔接的桥梁,在历年的高考试题中都占有重要位置．但是从试卷分析情况看,学生对数列知识的掌握和应用不容乐观．本文以2012年广东高考数学(理科卷)第19题为例,谈谈对该题的一些解题研究,希望能在解决数列综合题方面给大家一些有益的教学启发．

题目设数列{an}的前n项和为Sn满足2Sn=an+1-2n+1+1,n∈N*，且a1,a2+5，a3成等差数列.

(1)求a1的值；(2)求数列{an}的通项公式;(3)证明:对一切正整数n,有

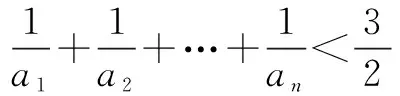
一、题目分析

题目主要考查了数列an与Sn的关系,等差中项的性质与等比数列的概念、性质、通项公式及求和公式,还有数列与不等式的综合．涉及到的数学思想与方法主要有:方程(组)思想的应用，转化与化归思想的运用，构造法、待定系数法、累加法、累乘法、数学归纳法、裂项相消法、放缩法等．

该题难度分三个层次,第(1)问属于基础题,第(2)问属于中档题,第(3)问是数列型不等式的证明,难度较大．题目的已知条件较少,明显条件为“2Sn=an+1-2n+1+1,n∈N*,且a1,a2+5,a3成等差数列”；隐含条件是等差中项的性质,以及an与Sn的关系,即Sn=a1+a2+…+an和an=Sn-Sn-1(n≥2).通过这些条件不难列出方程组求出a1的值,从而解决第(1)问．由于已知条件给出Sn与an+1的关系式,故第(2)问可归结为“知Sn求an”的问题,借助明显条件“2Sn=an+1-2n+1+1,n∈N*”和隐含条件“an=Sn-Sn-1(n≥2)”,运用化归思想使第(2)问得到解决．至于第(3)问数列型不等式的证明,显然要把第(2)问的结论作为已知条件使用,也就是说第(3)问的求解要依赖于第(2)问的顺利解答．该题的三个小问层层递进,紧密联系,前一问解答的正确与否直接关系到下一问的解答．

二、解题思路分析

1.对于第(1)问，

在2Sn=an+1-2n+1+1中

令n=1得2S1=a2-22+1,即

2a1=a2-3.

①

令n=2得2S2=a3-23+1，即

2(a1+a2)=a3-7.

②

再结合条件“a1,a2+5,a3成等差数列”又可得2(a2+5)=a1+a3.

③

联立①②③，解得a1=1.

在解决本题第(1)问时,估计学生的易错点主要有两个:一是审题不认真、细致,把数列{an}误以为是等差或等比数列,乱套其通项公式及求和公式．二是只会由明显条件列出一个关系式“2(a2+5)=a1+a3”,不善于发掘隐含条件,缺乏利用方程(组)的思想去解决问题．笔者认为,若把第(1)问改为“求a1,a2,a3的值”,学生可能会更容易联想到借助an与Sn的隐含关系．因此,在教学中,如果发现学生找不到思路时,可适当改动一下问题以作提示,让学生能更自然、更容易地联想到解题的方向和思路．另外,在求解方程组的过程中,估计学生主要采用以下两种策略:一是由① ② 得a2=2a1+3,a3=6a1+13,代入③ 解得a1=1.这是常规做法,把三元问题转化为一元问题解决．二是由②-③ 得a1=1，这种方法能结合该方程组的特点,迅速、快捷、一步到位就把问题解决．因此,在教学中,我们既要注重通法通则的教学,也要注重解题技巧的教学,鼓励学生尽量结合题目特点,选取最优算法以提升解题速度．

2.对于第(2)问

由2Sn=an+1-2n+1+1，得2Sn-1=an-2n+1(n≥2)，两式相减，可得2an=an+1-an-2n,即an+1=3an+2n(n≥2).接下来有3种不同的解题方法可供选择.

思路1(先变形再用累加法)

先两边同时除以3n+1,得

所以an=3n-2n(n≥2).

当n=1时，a1=1,也满足该式子,所以数列{an}的通项公式是an=3n-2n.

思路2(先变形再用构造法)

先两边同时除以2n+1,得

再通过待定系数法构造辅助数列求得an=3n-2n(n≥2)，进而由a1=1也满足该式得到通项公式an=3n-2n(n∈N*).

思路3(直接用构造法)

由an+1=3an+2n，得an+1+2n+1=3(an+2n),所以数列{an+2n}(n≥2)是一个以a2+4=5+4=9为首项，3为公比的等比数列.an+2n=9×3n-2,即an=3n-2n(n≥2)，当n=1时，a1=1，也满足该式，所以数列{an}的通项公式是an=3n-2n.

比较三种解题思路,思路1是先变形再用累加法,思路2、3都用到了待定系数法进行构造求解.区别在于解题思路2先变形再进行构造,解题思路3则是直接构造,解题看似思路3更为直接快速,但用待定系数法进行构造求解数列是学生理解上的一个难点.估计学生会对解题思路1的累加法过程更容易接受些,但前提条件是学生要会先做变形处理,化为形式“bn+1=bn+f(n)”．不管采取哪种解题思路,笔者估计学生在解答第(2)问过程中的易错点为:一是在利用“an=Sn-Sn-1(n≥2)”求解时,忽略了“n≥2”条件的限制,从而漏掉了对“当n=1时，a1=1,也满足该式子”情况的讨论．二是三种不同解法都要用到等比数列的通项公式或求和公式,由于有“n≥2”的限制,所以学生在套公式计算时,项数是n项?n-1项?还是n-2项?学生在此会比较容易出问题．

此外,笔者认为在课堂教学中对第(2)问还可进行这样的一个推广:

形如an+1=pan+qn(p≠1)型递推数列,求通项方法有以下三种方向:

再用累加法求通项.

(3)直接进行构造,设an+1+λqn+1=p(an+λqn).通过比较系数,求出λ,转化为等比数列求通项．

3.对于第(3)问

有以下四种不同的解题思路:

思路1(逐项放缩)

由3n-3n-1=2·3n-1≥2·2n-1=2n,

思路2(累乘法)

思路3(裂项相消法)

当n≥3时，

an=3n-2n=(1+2)n-2n

=1+C1n·2+C2n·22+…+Cn-1n·2n-1

>C2n·2n=2n(n-1).

又a2=5>2×2×(2-1),

所以an>2n(n-1)(n≥2),

综上，命题获证.

思路4(数学归纳法)

①当n=1时，显然命题成立；

②假设当n=k(k≥2,k∈N)时成立，则

即命题在n=k+1时也成立.

综合①②知，对一切正整数n,命题成立.

笔者认为该题是一道好题,问题设计逐层深入,有一定的区分度,让不同层次的学生能在该题的解答过程中有所体现．第(1)问属于基础题,考查的是数列的一些基本知识和解题的基本技能,这要求学生在平时的数学

学习中要夯实基础,加深对基础知识、基本技能和基本数学思想方法的认识．第(2)、(3)问需要学生有较强的思维能力,通过多角度观察题目特点,深入剖析其特征,沟通各类知识的联系,抓住规律去探求解决问题的方法,考查的是学生的综合能力和创新能力.要求学生善于把一般问题转化为特殊问题、把不熟悉的问题转化为熟悉的问题去解决,即化归的思想.这是学生较为薄弱的环节之一,需要学生在平时的学习中有意识地对做过的题目进行总结、反思和归类,把数学问题及其解决方法一一对应,并能触类旁及,举一反三．这样，不管题目怎样千变万化,但万变不离其宗,只要对症下药,问题便可以迎刃而解．