王刚陶++煜瑾

【摘要】三位省评优课一等奖获得者的同课异构，各有千秋，说明了一节“好课”没有固定的标准，没有程式化的设计，但教师一定要肯下功夫，投入真感情，琢磨新套路，注重课堂的真实性、生成性和师生交流的和谐性.

【关键词】真实性；生成性；和谐性；同课异构

教材对导数与函数单调性关系的解释隐藏较深，不易提炼教学主线.因此，不同的教师对教材的编写意图有着不同的理解，不同的教学策略产生了不同的效果，这也使我对如何实现课堂的高效有了一个新的认识.以下是笔者对其中三位一等奖的授课情况的对比分析.1三位教师的教学过程简介

1.1A教师的解释过程

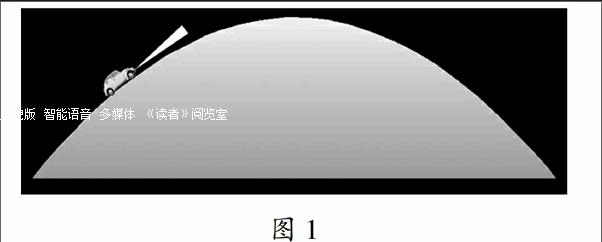
1.11问题情境：黑暗中，你是怎样通过远处汽车自身的灯光判断该车是上坡还是下坡的？

A教师利用生活中的常见问题：“汽车灯光的指向与上下坡之间的联系”，引导学生发现道路可以抽象成函数的图象，灯光可以抽象为切线（图1），这样，问题就转化为切线斜率与函数增减之间的联系，从而轻松高效地联系起导数与函数的单调性.

1.12猜想归纳：导数与函数的单调性有什么联系呢？

从图象上，我们发现，单调递增区间上，曲线呈上升趋势，函数单调递增，每一点处的切线倾斜角均为锐角，斜率大于0（图2）；在单调递减区间上，曲线呈下降趋势，函数单调递减，每一点处的斜线倾斜角为钝角，斜率小于0（图3）.

于是，可以猜想结论：对于函数y=f（x），

如果在某区间上f′（x）>0，那么f（x）为该区间上的增函数；

如果在某区间上f′（x）<0，那么f（x）为该区间上的减函数.

A教师从“形”的角度，对具体例子进行动态演示，通过观察、猜想到归纳、总结出结论，让学生体验知识的发现、发生过程.

1.13验证猜想：请举出几个常见的函数，探究导数与函数单调性之间的联系，验证前面猜想的结论.

函数f（x）=x3+xf（x）=exf（x）=cosx，x∈0，π

图象

单调性单调递增单调递增单调递减

导数

符号f′（x）=3x2+1>0f′（x）=ex>0f′（x）=-sinx<0，

x∈（0，π）

A教师通过师生合作，归纳已经学过的常见函数的特征，进一步验证了所猜想的结论的正确性.

1.14例题设置：

例1：确定函数f（x）=x2-4x+3在哪个区间上是增函数，在哪个区间上是减函数.

例2：确定函数f（x）=2x3-6x2+7在哪些区间上是增函数.

例3：确定函数f（x）=sinx（x∈（0，2π））的单调减区间.

变式：证明函数f（x）=sinx在区间（π2，3π2）上是单调减函数.

A教师从二次函数、三次函数到三角函数，让学生体会导数法研究函数单调性的一般性和普遍适用性.

1.2B教师的解释过程：

1.21认知冲突：是否能用已有的初等方法来确定函数f（x）=xlnx的单调区间？若不行，是否存在其它工具来研究该类函数的单调性.

B教师以学生的认知冲突为切入点，引导学生探究新方法，培养学生的好奇心，从而引入了导数工具，同时，让学生感受导数法研究单调性具有一般性和有效性.

1.22数形结合：

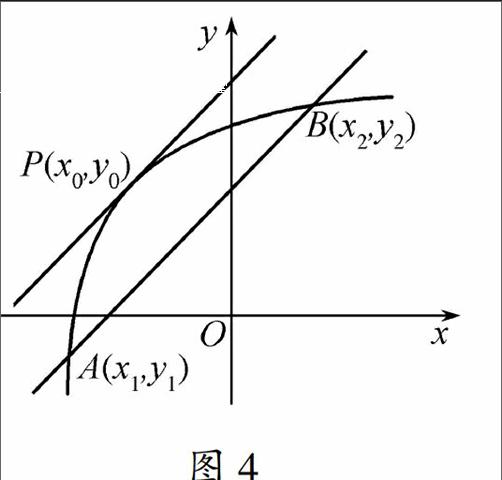
代数角度：函数y=f（x），在定义域内某区间I上，若对任意x1≠x2都有f（x1）-f（x2）x1-x2>0则函数在该区间上单调递增，此时区间I为单调增区间.图4

几何角度：在区间I上，存在x=x0，使得fx1-fx2x2-x1=f′x0>0（图4）.

故此，导数与函数单调性的关系为：

如果在某区间上f′（x）>0，那么f（x）为该区间上的增函数；

如果在某区间上f′（x）<0，那么f（x）为该区间上的减函数.

B教师采用中学生能够接受的方式引入了拉格朗日中值来证明上述结论，用直观的方法来分析和说明，培养学生严密的逻辑思维能力和意识.

1.23例题设置

证明函数f（x）=x3+x在R上单调递增.

变式1：确定函数f（x）=x3-x在哪些区间上是增函数.

变式2：确定函数f（x）=ex-x的单调区间.

变式3：你能编制出相应一道题目吗？

试结合y=x3思考：如果f（x）在某个区间上单调递增，那么在该区间上必有f′（x）>0吗？

B教师的例题设置从充分性与必要性两个角度来让学生理解导数与单调性的关系.

1.3C教师的解释过程：

1.31寻找共性

函数的单调性刻画了函数在某区间上的变化趋势（上升或下降的变化趋势）.

导数刻画了函数在某点处的变化趋势（图像经过该点时的上升或下降趋势）.

C教师基于学生的原有认知结构，从两点知识的功能出发，寻找共性，引导学生猜测两者之间可能存在的联系.

1.32定义再探

单调递增函数：函数y=f（x），在定义域内某区间I上，若对任意x1≠x2都有f（x1）-f（x2）x1-x2>0，则函数在该区间上单调递增.

几何解释：区间I上任意两点的割线斜率大于零则函数单调递增.

导数的定义：当Δx→0时，ΔyΔx=fx0+Δx-fx0Δx→f′x0.

几何解释：当割线两端点无限逼近时，割线斜率逼近切线斜率.

C教师引导学生从数学的本质“定义”出发寻找两者之间的关系，通过两个定义的再解释，发现割线的斜率是沟通导数与单调性之间的纽带.

1.33以直代曲

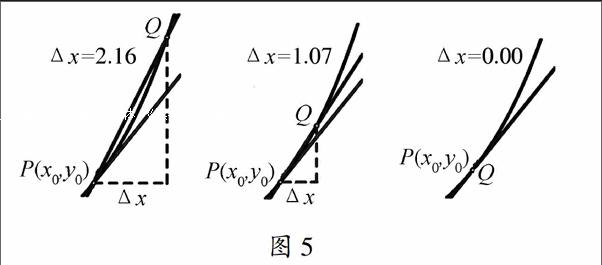
图5

随着点Q沿曲线向点P运动，割线PQ在P点附近越来越逼近曲线（图5），当点Q无限逼近P点时，割线PQ最终成为在P点附近最逼近曲线的直线切线l（图6）.图6

C教师利用导数的本质思想：“以直代曲”沟通了导数与单调性之间的关系，即曲线经过P的上升与下降的变化趋势可用P点处的切线斜率的正负来刻画.

1.34量到质变

若f′x0>0刻画的是曲线f（x）在点P0处的上升趋势，那么若对任意x∈a，b都有f′（x）>0时，则函数f（x）在a，b上单调性如何呢？

C教师运用“动点成线”的原理，由曲线经过某区间内的每一点的上升与下降趋势来刻画函数在该区间内的单调性，从而由量变到质变获得了结论.

1.35例题设置

例1：确定函数f（x）=x2-4x+3的单调区间.

例2：确定下列函数的单调区间.

（1）fx=2x3-6x2+7

（2）fx=xlnx

例3：请用导数证明f（x）=sinx-x在区间0，π上是减函数.

变式1：请思考该函数在区间-π，0、-π，π上的单调性？

变式2：请思考该函数在区间-π，π上导函数的符号？

变式3：结合以上问题判断，函数单调递减时，f′x<0一定成立吗？

C教师的例题设置除了让学生体会导数法研究函数单调性的一般性和普遍适用性以外，更利用例3的变式让学生理解了导数法判断函数单调性的非必要性.2教学目标的对比

教学目标是教学的航向，是教学成功与否的关键.三位教师的教学目标的主旨均为：理解导数与单调性的关系，掌握用导数法研究函数的单调性.通过课堂练习来看，三堂课学生基本都能掌握用导数法求解函数单调区间的步骤，然而在实现“理解导数与函数单调性的关系”这一目标时，三位教师所达到的效果不尽相同：A教师遵循的课堂展开思路是“猜想”——“验证”——“实践”，在这三个环节中结论是由不完全归纳得到，师生虽然花了大量的时间与例子去验证，但在实践过程中例题设置只是前者猜想归纳的简单重复，没有思维的层次性，学生没能理解.B教师的例题设计有了层次性，并且设置了一个开放性问题，让学生自主编写题目，教师由此引导学生进一步思考：若函数单调递增则f′（x）的符号是否一定为正？C教师的例题设置不仅完成了让学生巩固导数法求单调区间，并且每个例题都有其目的：例1的目的是让学生感受导数法的有效性；例2的目的是让学生感受导数法的一般性；例3及变式的安排是让学生感受导数法证明函数单调性的工具性及非必要性.从目标的完成度来说C教师完成的更好，更自然.3重难点突破方法的对比

从教学过程中可看出三位教师确定的重难点均为：探索函数的单调性与导数的关系.但三位教师对这个内容的理解角度不同，处理方式也就不同：A教师的探索过程是由不完全归纳法得到，缺乏严密的推理论证，并且该教师是由从函数的单调性得出导数的正负，但在应用时又将该结论对调，逻辑较为混乱.B教师从学生能接受的角度引入了拉格朗日中值定理，学生能在一定程度上理解该定理，但由于缺乏罗尔中值定理的铺垫，该定理的出现显得很突兀.C教师能从学生的原有认知结构出发，紧扣教材，从导数的根本含义“以直代曲”的角度出发，由点到线，逐步深入取得了十分好的效果.从思维层次与教学效果来看，C教师的设计显然更胜一筹.4总结

带评比性质的公开课是教学“示范园”，它更多的是引导教师怎样去做，它追求着这样一个境界：教师在课堂上语言生动，具有感染力；教态洒脱，富有激情；教法精当，洋溢着布局之美.学生在教师的鼓动和引导下，充满着生命的活力，课堂让他们感受到学习的快乐.然而我们是否更应该追求课堂教学的本真：课堂思维的深度，师生的思维交流，学生的教育引导，教学设计的特色.都说课堂教学是一门遗憾的艺术，所以课堂教学更不应该追求表面的完美，应该留有“遗憾”.