陈海波丁光涛许雪艳

（1.巢湖学院，合肥 238000）（2.安徽师范大学物理与电子信息学院，芜湖 241000）

关于变积的研究*

陈海波1丁光涛2†许雪艳1

（1.巢湖学院，合肥 238000）（2.安徽师范大学物理与电子信息学院，芜湖 241000）

研究变分法逆问题中变积概念及其计算方法.由变积直接构造的是与加速度相关的Lagrange函数，再通过规范变换可以得到位形空间中的Lagrange函数.这表明这种构造Lagrange函数的方法与Engels方法一致.

变分法， 逆问题， Lagrange函数， 变积， Engels方法

引言

变分法在力学物理学和工程科学中有重要的应用，其中积分形式的变分原理具有重要的理论价值，例如，力学和物理学中的Hamilton原理.由变分原理可以导出运动微分方程，求解这些方程能够讨论系统的运动，而现代计算机又使得变分问题的直接解法成为掌握系统实际运动的有效方法.一百多年来，变分法的逆问题也日益引人关注，其基本问题是，给定的系统运动微分方程能否从变分原理中导出？若能，如何构造对应的Lagrange函数？在这个领域已经取得很多重要成果［1-9］.我国一些学者曾经类比微分和积分这对正逆运算，提出变分的逆运算概念-变积［10］，但是未能深入讨论，而且长期以来对此问题的研究没有继续下去.本文将进一步探讨变积这个概念，给出其计算方法，讨论它与变分法逆问题理论中有关理论和方法的关系.最后，给出运用实例.

1 变积的提出

设完整的力学系统的Lagrange函数为L（t，q，˙q），时间t为自变量，广义坐标q是时间的函数，作用量为

计算作用量的变分，考虑一般端点条件，得到

本文采用求和约定，对同一项中的重复指标求和.系统沿真实路径运动时，作用量变分为零，即

由于函数的变更δqα是任意的，故从式（2）得到

方程（4）是系统的运动微分方程-Lagrange方程，端点条件（5）是一般形式的，表示在真实路径运动始末端点，系统的广义动量与广义坐标的变分正交.不难验证，对固定端点情况

条件（5）也满足.

文献［10］中引入变积概念，在此基础上，进一步给出明确的变积概念.式（2）所表示的作用量变分，是函数空间中函数qα及其邻近函数qα+δqα比较的变更.因此作为变分逆运算的变积应当是在qα的函数空间中积分，即从式（2）得到

下面证明由上式可以得到作用量表达式.利用分部积分，由（7）式导出

比较上式两端，得到作用量为

式（9）与式（1）相同，从式（7）到式（9）过程是从式（1）到式（4）的逆过程，即变积能够从Lagrange方程导出Lagrange函数，是变分的逆运算［10］.

下面的问题是要进一步研究这个新的概念，给出变积的具体计算方法.要进一步研究如何运用一般的积分计算来进行函数空间中的变积计算，使之成为处理变分法逆问题的一种适用方法.

2 变积的计算方法

2.1 变积的积分计算

在Lagrange力学逆问题中，一个反复研究的问题是如何直接从运动方程计算Lagrange函数，文献［10］提出的变积概念实质上是对此问题的又一种探讨.式（7）中的被积式是Lagrange方程本身，已经证明这样的方程是自伴随的.如果直接给出的方程是非自伴随的，必须首先变换成为自伴随方程，才能得到对应的Lagrange函数.如果给出的方程不能变换成为自伴随方程，则对这种方程就不存在对应的Lagrange函数［1-2］.本文下面的讨论都从自伴随方程出发，设给出一组方程为

满足如下条件

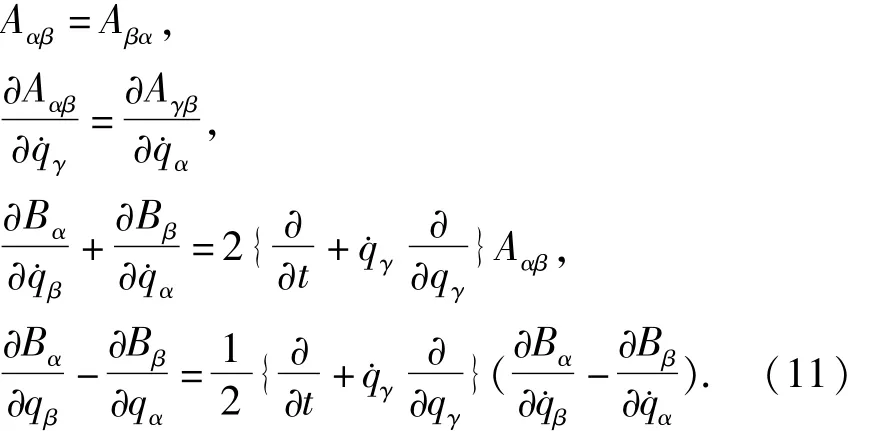
这组方程就是自伴随方程［1-2］，系统是Lagrange系统.

根据变积概念，力学系统（10）的Lagrange函数从下式开始计算

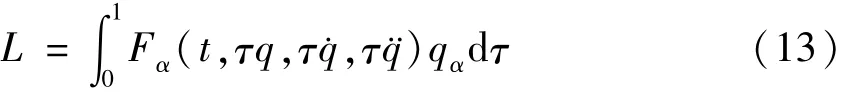
上式表明函数空间中的积分（13）是从选取τ为0表示起始路径q1，到τ＝1表示终末路径q2，即系统的真实运动路径q（q1，q2，…，qn）.这样的选择使得函数空间中的积分变换成为对单参数τ∈（0，1）的通常积分，条件（11）保证了式（13）导出的结果是满足式（12）的结果.

2.2 变积导出与加速度相关的Lagrange函数

然而，必须指出的是，直接从式（13）积分导出的Lagrange函数不是传统的位形空间中的Lagrange函数L（t，q，˙q），而是与加速度相关的二次Lagrange函数L（t，q，˙q，¨q）［4，5］，它显含广义坐标对时间的二次导数.由于式（10）是加速度的线性式，故这种函数L（t，q，˙q，¨q）也与广义加速度线性相关.根据广义力学，对二次Lagrange函数

的广义力学系统，Lagrange方程为

对式（10）的方程组，式（14）的Lagrange函数具体写成

但是，上式中含加速度项是能够利用规范变换消除，而得到位形空间中的Lagrange函数L（t，q，˙q）.设规范变换函数为G（t，q，˙q），直接计算可以证明

如果要求式（16）的Lagrange函数通过规范变换得到的与加速度无关，那么应当满足下列条件

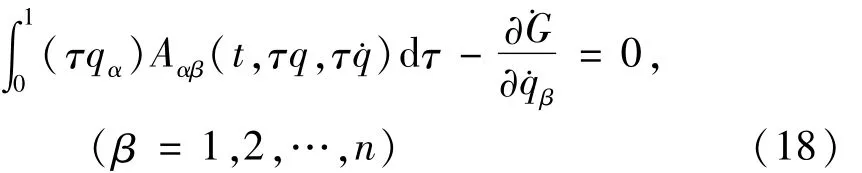
2.3 变积与变分法逆问题的Engels方法

由于方程（10）是自伴随的，系数Aαβ满足如下条件

故方程组（18）存在下列解

结合式（13），得到变积方法导出的自伴随方程组（10）的位形空间中的Lagrange函数

这个结果与变分法逆问题中构造Lagrange函数的Engels方法是一致的.如果给出的微分方程（组）是自伴随的，或者变换成为自伴随的，这个构造Lagrange函数的式（21）是一种常用的方法.还应当指出，式（21）与一些文献（如［1，2］）给的表达式存在符号上的差别，这是因为我们前面的推导中，对包含二阶导数的Lagrange函数的Lagrange方程是方程（15）.变换到只包含一阶导数的Lagrange函数情况时，方程（15）变换为

这种形式与通常的Lagrange方程也相差符号，但是，由于式（21）的Lagrange函数与传统的Lagrange函数符号相反，故从式（22）导出的方程就是正常的了.

综上所述，利用变分计算，可从系统的Lagrange函数L导出系统的Lagrange方程，这种形式的方程满足自伴随条件；利用变积计算，可以从系统的自伴随形式的运动方程构造Lagrange函数L.变分和变积这一对正逆运算可以写成

就构成了力学系统Lagrange方程和Lagrange函数之间互相变换的桥梁.

3 算例

以两个一维的简单系统为例，说明变积的计算方法的应用.

例1 简谐振子.简谐振子的运动微分方程为

这个方程是自伴随的.代入式（16），可以计算得到加速度相关的Lagrange函数

代入式（21）（或（24）），就得到位形空间中的Lagrange函数

这里与通常的Lagrange函数之间相差符号，前面已经给出说明.

通过直接验证自伴随条件，可以证明方程（25）变换成

仍然是自伴随方程.代入式（16），得到加速度相关的Lagrange函数

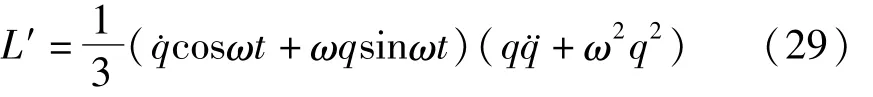
代入式（21）得到位形空间中的Lagrange函数

此例说明变积方法对计算Lagrange函数是有效的.

还应当指出，同一个简谐振子系统满足自伴随条件的运动微分方程有多种形式，例如式（25）和式（28），因此，导出的式（26）L与式（29）L′是同位等效的与加速度相关的Lagrange函数，式（27）与式（30）是位形空间中同位等效的Lagrange函数.事实上简谐振子系统存在很多不同的等效Lagrange函数，包括等效的Lagrange函数族［8，11］.

例2 Emden方程［7］

这是一个非自伴随方程，乘以因子t2就变换为自伴随形式

代入式（16），得到加速度相关的Lagrange函数

式（32）中A＝t2，利用式（21）导出位形空间中的Lagrange函数为

这个结果也与其它文献给出的结果相差符号.

4 结论

本文对文献［10］中提出的变积概念进行深入的再研究.通常分析力学中从作用量的变分导出系统Lagrange方程，本文从系统Lagrange方程或满足自伴随条件的运动微分方程的变积导出系统作用量，再导出系统Lagrange函数，从而表明变积运算是变分运算的一种逆运算.给出了从变积出发计算Lagrange函数的具体的积分方法，并且指出直接利用这种方法计算系统的自伴随运动微分方程，导出的结果是与加速度相关的Lagrange函数，进一步利用规范变换能够将这种Lagrange函数变换成为位形空间中通常的Lagrange函数.上述完整的变积计算过程与构造Lagrange函数的Engels方法一致，由此也可以这样说，变积概念的提出给出了Engels方法的一种新解释.

1 Santilli R M.Foundations of TheoreticalMechanics I.New York：Springer-Verlag，1978

2 Santilli R M.Foundations of Theoretical Mechanics II. New York：Springer-Verlag，1983

3 Musielak Z E.Standard and non-standard Lagrangians for disspative dynamical systems with variable coefficient. Journal of Physics A：Mathematical and Theoretical，2008，41：055205

4 丁光涛.经典力学中加速度相关的Lagrange函数.物理学报，2009，58（6）：3620～3624（Ding G T.Acceleration-dependent Lagrangians in classical mechanics.Acta Physica Sinica，2009，58（6）：3620～3624（in Chinese））

5 丁光涛.计算加速度相关Lagrange函数的方法.物理学报，2009，58（10）：6725～6728（Ding G T.A method for computing acceleration-dependent Lagrangians.Acta Physica Sinica，2009，58（10）：6725～6728（in Chinese））

6 CieSliński J L，Nikiciuk T.A direct approach to the construction of standard and non-standard Lagrangiqns for dissipative-like dynamical systems with variable coefficients. Journal of Physics A：Mathematical and Theoretical，2010，43：17250

7 丁光涛.一维变系数耗散系统Lagrange函数和Hamilton函数的新构造方法.物理学报，2011，60（4）：44503（Ding G T.A new approach to the construction of Lagrangians and Hamiltonians for one-dimensional dissipative systems with variable coefficients.Acta Physica Sinica，2011，60（4）：044503（in Chinese））

8 丁光涛.从第一积分构造Lagrange函数的直接方法.动力学与控制学报，2011，9（2）：102～106（Ding G T.A direct approach to construction of the Lagrangian from the first integral.Journal of Dynamics and Control，2011，9（2）：102～106（in Chinese））

9 丁光涛.一类Painleve方程的Lagrange函数族.物理学报，2012，61（11）：110202（Ding G T.The families of Lagrangians of a Painleve equation.Acta Physica Sinica，2012，61：110202（in Chinese））

10 Liang L F，Shi Z F.On the inverse problem in calculus of variations.Applied Mathematics and Mechanics，1994，15：815～830

11丁光涛.关于谐振子第一积分的研究.物理学报，2013，62（6）：064502（Ding G T.A study on the first integrals of harmonic oscillators.Acta Physica Sinica，2013，62（6）：064502（in Chinese） ）

method

A STUDY OF VARIATIONAL INTEGRAL*

Chen Haibo1Ding Guangtao2†Xu Xueyan1
（1.Chaohu College，Hefei 238000，China）
（2.College of Physics and Electronic Information，Anhui Normal University，Wuhu 241000，China）

The concept and the calculation of variational integral in the inverse problem of variational calculus are studied.What is constructed by variational integral directly is the acceleration-dependent Lagrangian，which can be transformed into the Lagrangian in configuration space by the use of gauge transformation.It is indicated that themethod to construct the Lagrangian is consistentwith Engels′method.

calculus of variations， inverse problem， Lagrangian function， variational integral， Engels′

10.6052/1672-6553-2016-007

2015-11-24收到第1稿，2015-12-05收到修改稿.

*国家自然科学基金资助项目（11472063）

†通讯作者E-mail：dgt695＠sina.com

Received 24 November 2015，revised 5 December 2015.

*The project supported by the National Natural Science Foundation of China（11472063）.

†Corresponding author E-mail：dgt695＠sina.com