王晓敏, 赵喜杨, 姚　兵

(西北师范大学 数学与统计学院， 甘肃 兰州 730070)



关于树的若干等价性命题

王晓敏, 赵喜杨, 姚兵*

(西北师范大学 数学与统计学院， 甘肃 兰州 730070)

摘要：给出15种关于树的等价性命题, 为更好地发挥树在网络研究中的作用提供依据，为这15个等价命题提供了简单而新的证明。

关键词:树；生成树；圈；路；度数

MR subject classification: 05C05, 05C69, 05C82

树在各种网络、程序设计、物流运输、电路设计、化学结构等领域有着广泛的应用。例如, 利用生成树来寻找无标度网络的关键节点以及用树来确定网络的控制集等, 还可以利用无标度生成树来确定动态网络的拓扑结构, 揭示现实网络存在的规律性。在数学的分支图论中, 树是除路和圈之外最简单的图类, 人们用它来刻画许多的图类以及图的性质。最典型的是, 有关树的数学猜想非常多[1]。例如, 著名的优美树猜想[2], 这个猜想的解决就可以导致诸如Ringle猜想[3]等若干猜想的解决。此外, 在研究一些悬而未决的问题往往从树这种情形开始着手[4-5], 如直径为4的优美树[6]、 最优树的若干问题[7]、 弱优美树及其应用[8]。因此, 对树的深入研究不仅是数学理论的需要, 更重要的是为研究实际网络提供可靠的理论依据和可行的技术手段。

文中所考虑的图均为有限、无向、简单图, 没有定义的术语和符号参考文献[12]。我们把度数为1的顶点称为叶子。用p(G)和q(G)分别表示图G的顶点个数和边的数目。n个顶点的完全图记为Kn, 只有一个顶点的图记为K1。符号nd(G)表示图G中度数为d的顶点的个数。缩边图G·e是删去图G的边e并将边e的2个端点重合所得到的图。对图G的2个不相邻的顶点u和v添加边uv=e+, 再删除图G的一条不是边e+的边e-, 称这种运算为(e+,e-)-运算, 也说对图G实施了一次(e+,e-)-运算。

1结论及其证明

定理设图G是非平凡简单图, 下面的命题两两等价:

(1) 图G连通且无圈[9]。

(2) 对p个顶点的连通图G实施一系列(e+,e-)-运算后, 总可以得到一条p个顶点的路。

(3) 图G的任意一对顶点由唯一的一条路连接[9]。

(4)G恰有p(G)[p(G)-1]/2条路, 且任意一对顶点至少由一条路连通[12]。

(5) 对于任意的边e∈E(G),G是使得图G-e不连通的最小连通图[12]。

(6)G是连通图, 且q(G)=p(G)-1[9]。

(7)G是无圈图, 且q(G)=p(G)-1[9]。

(10) 令连通图G=G0, 则存在k≥1, 使得图Gi(i=1、2、…、k)至少含有Δ(Gi)片叶子, 删去图Gi的Δ(Gi)片叶子得到图Gi+1, 且Gk=K1。

(11) 图G的每条边都是图G的割边, 且q(G)=p(G)-1[12]。

(12) 图G的每个度数不为1的顶点都是图G的割点, 且q(G)=p(G)-1[12]。

(13) 图G连通, 对于任意的边e∈E(G), 图G的生成树的个数等于缩边图G·e的生成树的个数。

(14) 当m≥3时, 连通图G不是完全图Km, 且对图G的任何2个不相邻的顶点u和顶点v添加边uv, 则图G+uv含有唯一的圈[9]。

(15) 设G≠K1∪K3或G≠K2∪K3, 且q(G)=p(G)-1,对于图G中任何2个不相邻的顶点u和顶点v添加边uv, 则图G+uv包含唯一的圈[9]。

证明以下用符号(i)⟹(k)表示从命题(i)来证明命题(k), 1≤i,k≤15以及i≠k。

(1)⟹(2)，因p个顶点的图G连通, 如果图G有圈, 则对图G实施一次(e+,e-)-运算不能减少圈的数目,即无论实施多少次(e+,e-)-运算, 都得不到一条路, 矛盾。从而, 图G无圈。若图G为路, 证明完成。如果图G不是路, 则图G的叶子数目n1(G)≥3,其中有2片叶子x、y在图G的路P=xu1u2…uky上, 另外一片叶子w与图G的顶点w′ 相邻。对图G实施一次(e+,e-)-运算, 其中e+=yw,e-=ww′, 得新图G1的路P+yw。易知,n1(G)≥n1(G1)。如此进行下去，存在k使得Gk是一条p个顶点的路。命题(2)得证。

(2)⟹(3)，由于图G的任何一对顶点u和顶点v之间至少有一条路P(u,v)，则G是连通图。反设顶点u和顶点v之间的路不唯一, 假设顶点u和顶点v之间存在另外一条不同于路P(u,v)的路Q(u,v)，说明图G含圈, 则对图G实施多少次(e+,e-)-运算不能减少圈的数目, 即得不到一条路，矛盾于命题(2)。

(3)⟹(4)，考虑到图G的任何一对顶点之间都有一条路, 故图G是连通的, 这导致图G至少有p(G)[p(G)-1]/2条不同的路。如果图G有多于p(G)[p(G)-1]/2条路, 将产生一对顶点至少有2条路, 这冒犯命题(3)。

(4)⟹(5)，反设命题(5)不成立, 即图G有一条边e, 使得删去边e的余图G-e是连通的, 可导出图G-e至少有p(G-e)[p(G-e)-1]/2条不同的路。注意到,p(G)=p(G-e), 推出图G至少有1+p(G)[p(G)-1]/2条不同的路, 与命题(4)冲突。

(5)⟹(6)，对图G的顶点数目p(G) 使用归纳法。当p(G)=2时，余图G-e不连通，又一条边仅能连2个分支G1、G2。得 |V(G1)|=|V(G2)|=1, 可算出q(G)=1=2-1=|V(G1)|+|V(G2)|-1=p(G)-1。设当p(G)=k时，命题(6)成立。考虑p(G)=k+1时的情形。由于对任意一条边e∈E(G)，图G-e不连通，且G-e有2个分支H1、H2。由归纳法，知q(Hi)=p(Hi)-1,i=1、2。从而，有q(G)=q(H1)+q(H2)+1=p(H1)+p(H2)-2+1=p(G)-1。由于圈上的边e皆不能使得G是图G-e不连通的最小连通图，故G无圈。命题(6)获证。

(6)⟹(7)，反设图G含圈, 则删去圈中的任意一条边e, 得到的图G-e仍连通, 若G-e含圈C, 则继续删除圈C上的一条边, 如此下去, 直到所得到的图不含圈。设这样删除的边的集合为E1, 显然G-E1是连通图且不含圈, 并有q(G-E1)=p(G-E1)-1, 注意到p(G-E1)=p(G), 则有

q(G)=q(G-E1)+|E1|=

p(G-E1)-1+|E1|=

p(G)+|E1|-1≥p(G),

矛盾于命题(7)。

(7)⟹(8)，反设图G有m(m≥1) 个分支G1、G2、…、Gm, 其中m≥2。根据命题(7), 每个分支Gi满足q(Gi)=p(Gi)-1(i=1、2、…、m)。由于图G的边数目

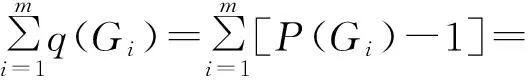
p(G)-m,

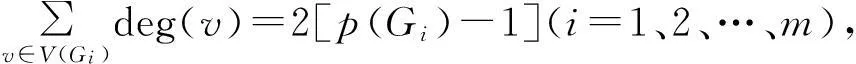
2p(G)-2m。

这与命题(9)冲突, 亦即图G是连通图。由于

2+[Δ(G)-2]nΔ(G)(G) ≥Δ(G),

且Δ(G)>0 (图G是非平凡图), 说明图G至少有Δ(G)片叶子, 则可以删去图G的Δ(G)片叶子, 得到一个连通图G1；又因G1连通，命题(9)保证

Δ(G1)>0,

所以图G1至少有Δ(G1)片叶子, 删去它的Δ(G1)片叶子后, 得到图G2；如此进行下去, 由于图G的顶点数目有限, 依次可得图G0、G1、…、Gk, 其中G=G0和Gk=K1, 且每个图Gi至少有Δ(Gi)片叶子, 删去图Gi的Δ(Gi)片叶子就得到图Gi+1(i=0、1、2、…、k-1)。

(10)⟹(11)，如果图G有一条非割边xy, 则边xy在图G的一个圈C上。由于圈C上的顶点不是叶子, 亦即, 依次删去叶子最后所得到的图Gk总含圈C, 即Gk≠K1, 与命题(10)矛盾。图G的每一条边都是割边，说明图G不含圈。如果图G不连通, 设它有分支G1、G2、…、Gm(m≥2)。根据命题(10)，每个Gi对应图Gi,1、Gi,2、…、Gi,mi, 其中Gi,mi=K1, 删去图Gi,j的Δ(Gi)片叶子就得到图Gi,j+1(j=0、1、2、…、mi-1)。当m≥2时，进行删去叶子运算，最后得到m个K1，与命题(10)矛盾，只有图G不含圈且连通，这导致q(G)=p(G)-1。

(11)⟹(12)，假定图G有一个度数不为1的顶点w是图G的割点,即图G-w的分支数目与图G的分支数目相同, 则与顶点w相邻的每一个顶点都不是叶子。任取顶点w的邻点z, 删去边wz所得的余图G-wz的分支数目与图G的分支数目相等, 即边wz不是图G的割边, 这与命题(11)相悖, 说明图G的每一个度数大于1的顶点均为图G的割点。由q(G)=p(G)-1立得命题(12)。

(12)⟹(13)，设e=uv是图G的任意一条边。收缩边e=uv后得到缩边图G·e, 记顶点u与顶点v重合后的顶点为w*。命题(12)指出图G无圈, 且q(G)=p(G)-1。由(7)⟹(8), 从而图G和缩边图G·e均有生成树。如果图G的生成树的个数不等于缩边图G·e的生成树的个数, 则图G含有不通过边e的生成树,亦即, 图G有一个包含边e的圈, 相应地, 在缩边图G·e里可以找到一个包含顶点w*的圈。以上事实推出q(G)≥p(G), 但这与命题(12)冲突。

(13)⟹(14)， 在命题(13)下, 图G有生成树, 则图G连通；并且, 图G的生成树的个数等于缩边图G·e的生成树的个数, 保证图G不含圈，自然有图G不是完全图Km(m≥3)。因为图G至少包含一对不相邻的顶点u和顶点v, 给图G添加边uv后, 得到图G+uv。如果图G+uv包含2个圈C和C′, 则圈C和C′有且仅有一条公共边uv。那么, 删去边uv, 圈C和C′合并成图G的一个圈, 矛盾于图G不含圈，即矛盾于命题(13)。故命题(14)得证。

(14)⟹(15)，当p(G)=2时, 无意义, 以下设p(G)≥3。由命题(14)的条件, 图G连通且不是完全图Km(m≥3)。注意到，命题(15)的条件q(G)=p(G)-1≠p(G)[p(G)-1]/2,也说明图G不是完全图。如果G≠K1∪K3或G≠K2∪K3, 这与命题(14)冲突。按照命题(14), 连接图G的2个不相邻的顶点u和v, 加边图G+uv仅含唯一的圈, 命题(15)得证。

(15)⟹(1)，假定图G不连通, 即图G至少含有2个分支G1和G2。当|G1|+|G2|=4时, 命题(15)保证G≠K1∪K3, 故连接图G的2个不相邻的顶点u和v所得到的加边图G+uv不含圈, 矛盾于命题(15)。当|G1|=2和|G2|=3时, 命题(15)保证G≠K2∪K3,连接图G的2个不相邻的顶点u和v, 则图G+uv不含圈, 矛盾；当|G1|=1和|G2|=4时, 命题(15)条件q(G)=p(G)-1意味着G2等于4个顶点的圈, 连接这个圈上的2个不相邻的顶点x和y, 则图G+xy含2个圈, 与命题(15)冲突。当|G1|+ |G2|≥6时, 如果|G1|≤2和|G2|≥4, 容易找到矛盾点；如果|G1|≥3和|G2|≥3, 命题(15)条件q(G)=p(G)-1约束分支G1和G2中至多一个有圈, 不失一般性,G2含圈。但是, 连接分支G1的2个不相邻的顶点s和t, 则图G+st至少含2个圈, 与命题(15)矛盾。当图G有3个以上的分支时, 选取G1和G2是最大或次最大的分支, 其余论证相同于上面的论证。注意, 当图G有3个以上的分支时, 取前面2个分支的顶点u∈G1和顶点v∈G2, 给顶点u和顶点v连上一条边uv, 所得到的加边图G+uv不含唯一圈, 矛盾。说明假设图G不连通是错误的。图G连通结合命题(15)条件立得命题(1)。

上述证明过程表明：对1≤i,k≤15, 且i≠k时, 命(i)成立的充要条件是命题(k)成立, 定理得证。

2结语

以上等价命题各有利弊, 但是从多个角度、宽领域地刻画了树。不难看到：命题(1)不仅是树的定义最常用的方式, 而且容易在实际当中使用。命题(3)和命题(4)分别从路的唯一性和路的数目的方向进行论证，实际网络研究中不易运用。命题(5)较为抽象，属于极值类刻画。命题(6)和命题(7)由顶点数和边数的关系分别引出了无圈和连通的结论。命题(9)给出了叶子顶点的数目, 可以用命题(9)的方式来建立平面图的面数目与度为d的顶点个数之间的关系式。反复使用命题(10), 最终使得图收缩到一个顶点的完全图K1, 可以用来寻找网络中的关键节点。命题(11)和命题(12) 从割边和割点的角度阐述了有关图的连通性, 命题(13)是比较隐晦的有关树的命题，适用于归纳法讨论的情形。命题(14)的条件弱于命题(15)。再有, 我们认为“连通图G任何一个连通子图皆是树”是一个平凡的等价性命题, 因而没有将它放进前面的定理中。

本文中举例给出的等价性命题可以平行地建立图论中“森林”概念的等价性命题。

后续研究中，以下问题值得注意：是否存在不同于本文的其他非平凡的树的等价命题？

致谢感谢审稿人对本文提出的宝贵意见和指导性建议, 使得本文趋于严谨和完善, 并激发作者又找到树的一个等价命题。

参考文献:

[1] JOSEPH A G. A dynamic survey of graph labelling [J].The Electronic Journal of Combinatorics,2009,14:6.

[2] ROSA A．On certain valuations of the vertices of a graph[C]∥Theory of Graphs, International Symposium.New York: Gordon and Breach, 1967: 349-355．

[3] RINGEL G．Problem 25 in theory of graphs and its applications[C]∥FIEDLER M．Proceeding of the 4th international symposium smolenice．Prague: Czech Academy of Science, 1963: 162-167．

[4] 程世辉, 高景丽.树的等价定义及其证明[J]. 河南教育学院学报(自然科学版), 2003, 12(2):65.

[5] 田有先.关于树图的四个等价概念[J].达县师范专科学校学报(自然科学版), 1999, 9(2):23.

[6] 吕雪征.直径为四的优美树[J]. 华中师范大学学报(自然科学版), 2000, 34(2):144-149.

[7] 罗强, 宋朝红.最优树的若干问题[J].华中师范大学学报(自然科学版), 1997, 31(2):145-147.

[8] LI S C, MAO J Z, FENG Y Q. The weakly graceful tree with application [J].华中师范大大学学报 (自然科学版), 1998, 32(4):269-272.

[9] HARARY F. Graph theory[M].New York:Addison-Wesley, 1969.

[10] 郝玲.关于树的等价定义的证明[J]. 承德民族师专学报, 2004, 24(2):14.

[11] YAO B, ZHANG Z F, WANG J F. Some results on spanning trees[J]. Acta Mathematicae Applicatae Sinica: English Series, 2010, 26(5).607-616.

[12] BONDY J A, MURTY U S R. Graph theory with applications[M].New York:The MaCmillan Press Ltd, 1976.

〔责任编辑宋轶文〕

On equivalent definitions of trees

WANG Xiaomin, ZHAO Xiyang, YAO Bing*

(College of Mathematics and Statistics, Northwest Normal University,Lanzhou 730070, Gansu, China)

Abstract:15 proposition of trees that are equivalent to each other are obtained to deeply understand trees and dig more properties of trees in order to provide useful bases for network study. It is shown that simple and new proofs for the equivalencies of theses 15 propositions.

Keywords:tree; spanning tree; cycle; path; degree.

中图分类号：O157.5

文献标志码：A

*通信作者：姚兵, 男,教授。 E-mail: yybb918@163.com

基金项目：国家自然科学基金(61163054, 61163037, 61363060)

收稿日期：2015-06-16

doi:10.15983/j.cnki.jsnu.2016.02.123

文章编号：1672-4291(2016)02-0011-04

第一作者： 王晓敏, 女,硕士研究生, 研究方向为复杂网络。E-mail: 704944897@qq.com