Jens Høyrup

(RoskildeUniversity)

Seleucid, Demotic and Mediterranean Mathematics versus Chapters VIII and IX of theNineChapters: Accidental or Significant Similarities？*

Jens Høyrup

(RoskildeUniversity)

Similarities of geometrical diagrams and arithmetical structures of problems have often been taken as evidence of transmission of mathematical knowledge or techniques between China and “the West”. Confronting on one hand some problems from Chapter VIII of theNineChapterswith comparable problems known from Ancient Greek sources, on the other a Seleucid collection of problems about rectangles with a subset of the triangle problems from Chapter IX, it is concluded,(1)that transmission of some arithmetical riddles without method-not “from Greece” but from a transnational community of traders-is almost certain, and that these inspired the Chinese creation of thefangchengmethod, for which Chapter VIII is a coherent presentation;(2)that transmission of the geometrical problems is to the contrary unlikely, with one possible exception, and that the coherent presentation in Chapter IX is based on local geometrical practice.

NineChaptersonArithmetic,Fangchengmethod, transmission, mathematical riddles, Babylonian geometry

Yvonne Dold-Samplonius

inmemoriam

Received：2016- 08- 04Biography：Jens Høyrup, Roskilde University, Section for Philosophy and Science Studies. Email: jensh@ruc.dk. Homepage: http://ruc.dk/～jensh.As a historian of science, Høyrup has mainly worked on premodern Near Eastern, Mediterranean and European mathematics, but also in the border area between philosophy of science, sociology and history.

* This paper is a contribution to the workshop Mathematical Texts in East Asia Mathematical History, Tsinghua Sanya International Mathematics Forum, March 11-15, 2016.

Two pictures and a winged transmission

First of all, as introduction, two pictures.

Fig.1

To the left, the decoration of the “Mathematics and Systems Science” tower in the campus of the Chinese Academy of Sciences in Beijing, borrowed from Zhao Shuang’s third-century CE commentary to theGnomonoftheZhou-cf. (Cullen 1996: 206; Chemla & Guo 2004: 695-701); to the right, my own diagram reconstructed from the description of the procedure of the Old Babylonian problem Db2- 146 (c. 1775 BCE), in which the sides of a rectangle are to be determined from its area and the diagonal (Høyrup 2002a: 257-259). When I first made it, it should be added, I did not know about the Chinese diagram.

A first reaction may be that the two must be connected; indeed, when Joseph Needham (1959: 96 n.a, 147) finds the same diagram in Bhaskara II (he gives no reference) and believes it to be found nowhere else, he deems it “extremely probable that Bhaskara’s treatment derives from” Zhao Shuang’s commentary.

A connection between a Mesopotamian and a Chinese diagram is certainly not to be excludedapriori. There can be no doubt that the shared problem of the “hundred fowls” is really shared, and thus that some kind of mathematicsdidtravel.*For the moment I shall pretend that the notion of “shared problem” (or shared mathematical knowledge) is unambiguous; this corresponds to such classical discussions of inter-cultural mathematical connections as (Hermelink 1978) and (Vogel 1983). In the context of these discussions it was perhaps unproblematic to leave that semantic point to the understanding of the reader. We shall see below that it is not so for the present topic-but clarification is better postponed until we have our hands on material where it can be done concretely.The earliest known occurrence of this problem type is in the fifth-centuryZhangQiujianSuanjing(van Hée 1913), but soon it turns up not only with the same mathematical structure but also with shared parameters and dress (100 units of different prices and a total price of 100-only the choice of species and their individual prices vary) in Carolingian Western Europe, in India and in the Islamic World-see, e.g. (Libbrecht 1974); this cannot be imagined to be an accident.

We may add an observation, elementary but to my knowledge not made before. The early Islamic, Indian and Chinese occurrences speak of fowls, the CarolingianPropositionesadacuendosiuvenes(Folkerts 1978) has various dresses but none with fowls. This supports Jean Christianidis’ suggestion (1994: 240f) that the problem has developed from an early form represented in a Greek papyrus from the second century CE, where the units are already 100 but the price 2500.*Text in (Winter 1936: 39).Once the more striking version 100/100 was invented, that was the one that spread east and west-but the fowls only eastward, for which reason this latter invention can be presumed to be a secondary accretion.

Other possible interactions

The hundred fowls is an arithmetical riddle. Another arithmetical riddle thatmayhave travelled far is the one known in the cultures connected to the Mediterranean as the “purchase of a horse”. Like the “hundred fowls” it circulated with varied numerical parameters, but a typical example states that three men go to the market in order to buy a horse. The first says that he has enough to pay the price if he can have half of the possession of the other two; the second only needs one third, the last only one fourth of what the other two have. The possession of each and the price of the horse is asked for. Sometimes the price of the horse is given.

The problem seems to be hinted at in book I of Plato’sRepublic(333BC).*Trans. (Shorey 1930: I, 332f) Socrates asks when one needs an expert; and as usually he answers himself: for example when you go to the market to buy or sell a horse in common. Since horses did not serve in agriculture but only for military purposes, they would never be bought in common in real life. (I owe the discovery of the Platonic passage to the late Benno Artmann).In any case there can be no reasonable doubt that it turns up, undressed as pure-number problems, in Diophantos’ArithmeticaI:24-25(Tannery 1893: I, 56-69); the preceding propositions 22-23, moreover, ask a question which, if dealing with a purchase, would make each participant ask for the fractions 1/3,1/4 and 1/5 respectively 1/3,1/4,1/5 and 1/6 of the possession not of all the others but of the one that precedes in a circle.

The latter type has an interesting parallel in Chapter VIII, problem 13 of theNineChapters*My English from the French of (Chemla&Guo 2004: 643).:

Let us assume that with five families sharing a well, that what is missing for the two ropes ofJia(in order to reach the bottom of the well), that is as one rope ofYi, that what is missing for the three ropes ofYi, that is as one rope ofBing, that what is missing for the four ropes ofBing, that is as one rope ofWu, that what is missing for the six ropes ofWu, that is as one rope ofJia; and that, if each gets the rope that is missing for him, all will reach the bottom of the well. One asks for the depth of the well and for the length of the ropes.

The mathematical structure of the problem is the nearly the same, including the characteristic attractive sequence of fractions. However, one ofnropes is spoken of instead of the fraction 1/nof the totality of the ropes of each (which avoids the need to cut the ropes); moreover, the request is made to the following participant, not to the predecessor in the circle.

Problems 3 and 12 (ibid. p. 625, 641) are determinate but otherwise similar in structure. No. 3 speaks of 2 bundles of millet of high quality, 3 of medium quality and 4 of low quality, and in similar combinations they are to produce 1dou; no. 12 deals with the hauling capacity of horses of different strength. Problems 14 and 15 (ibid. pp. 645, 647) are sophisticated variants-we shall return to them.

The coincidences may seem striking-but are they evidenceofconnectionorofparallelexperiencesof fascination？Ifthe far from obvious dress had also been shared, as in the case of the hundred fowls, then connection would seem next to certain. Since it is not, we cannot decide on the basis of these problems alone.

However, problem 10 (ibid. p. 639) supports the connection hypothesis. It presents us with something like a two-participant version of the problems we have just examined. Two persons own money; ifJiagets half of whatYipossesses, he will have 50 coins; and ifYigets 2/3 of whatJiapossesses, he will have as much.

With only two participants, there is no difference between Diophantos’s two types. We notice, firstly, that here fractions and not “one out ofn” are spoken about; secondly, that the dress is the familiar “give-and-take” type.

This dress is used for a slightly different mathematical structure in problems from late Mediterranean Antiquity (and later). In Book XIV of theGreekAnthology(Paton 1916: V, 105), no. 145 runs

A. Give me ten minas, and I become three times as much as you.B. And if I get the same from you I am four times as much as you.

No. 146 uses different numerical parameters (two minas, twice, four times) but is otherwise identical. Prop. XV of Diophantos’sArithmeticaI (Tannery 1893: I, 36f) is an undressed version of the same problem type.

On the other hand, Fibonacci’s first example of a “purchase of a horse” (Boncompagni 1857: 228)has the same mathematical structure as the Chinese give-and-take problem, apart from being indeterminate. In Fibonacci’s problem, the first man asks for 1/3 of the possession of the second, while the second asks for 1/4 of what the first has. In both cases, each will have enough to buy the horse (whence the same amount).

Again, this coincidence in isolation suggests but does not prove a connection. However, the alternative explanation here cannot be fascination with interesting numbers but only accident. If we take together all the problems we have looked at, independent invention in the two areas becomes unlikely-not least because the case of the “hundred fowls” provides us with firm evidence that transmission could and sometimes did take place.

But what exactly can have been transmitted？ All these problems from theNineChapterscome from Chapter VIII, and all are used to train thefangchengmethod. Diophantos’s methods are quite different-and no closer are variants of the “Bloom of Thymarides” (Heath 1921: I. 94-96), which may have been used already around or before Plato’s times to solve similar problems.

In connection with the “hundred fowls”, Ulrich Libbrecht(1974:313) points out that

This implies that several mathematical problems were transmitted only as questions, without any method, as we can clearly state in Alcuin’s work (thePropositionesadacuendosiuvenes/JH); in different places methods were developed-wrong or right-to solve these problems. Perhaps they were considered more as games than as serious problems, as we can prove from several Chinese and European works.The same is clearly the case here. In terms I have used in (Høyrup 1990) (not knowing by then about Libbrecht’s observation), the problems have circulated as “subscientific” mathematics, more precisely as professional riddles belonging to an environment of mathematical practitioners; once taken up by groups which in some way can be characterized as scholarly mathematicians,*That is, people who are engaged in or linked to a school-based (as opposed to an apprenticeship-based) educational system, and who in that connection shape and transmit mathematical knowledge.these developed their own ways to deal with them, and in some cases they expanded the range of questions these methods could be applied to. Since the riddles functioned precisely asriddlesin the community of practitioners (in anthropological parlance asneckriddles-who is not able to solve them is “not one of us”) it is not even certain that the practitioners always had amathematicalmethod for solving them-a riddle asks for an answer, not for a calculation or a logical derivation, and a guess followed by a verification may have been enough.*This is precisely what Abū Kmil reproaches those who took pleasure in the “hundred fowls” in his times and surroundings-it was “a particular type of calculation, circulating among high-ranking and lowly people, among scholars and among the uneducated, at which they rejoice, and which they find new and beautiful; one asks the other, and he is then given an approximate and only assumed answer, they know neither principle nor rule in the matter”-my translation from (Suter 1910: 100).

That is where problems no. 14 and 15 of Chapter VIII of theNineChapterscome in. No. 14 deals with groups of unit fields of millet with different yields-say 2A, 3B, 4Cand 5D. But this time 2A+B+C=3B+C+D=4C+D+A=5D+A+B=1dou. This is too complex to present a nice recreational riddle-to keep track of it without material support would be difficult. No. 15 deals with three groups of bundles of millet of different weights but speaks of differences instead of sums-in symbols, 2A-B=3B-C=4D-A=1dan.

Such extensions of the range of “recreational” riddles by variation and systematization at the hands of scholarly mathematicians are a common occurrence in history, from Old Babylonian times to Pedro Nuez and beyond. Diophantos, inArithmeticaI, replaces variation by generalization-but his choice of numerical examples betrays the recreational starting point.

At times, however, “scholarly mathematicians” have made a further step, and used the recreational material as the starting point or inspiration for the creation of a whole mathematical discipline. That is the way Old Babylonian second-and third-degree “algebra” was generated.*See, for instance, (Høyrup 2001).In the whole corpus, there is not a single second or third-degree problem derived from a genuine practical question that might present itself to a Babylonian scribal calculator. We should not be misled by the fact that theentitiesoccurring as “unknowns” in the problems would be familiar to him-dimensions of fields and excavations, prices, manpower, etc. In genuine surveying, one would (for instance) never have to determine the sides of a rectangular field from its area and the sum of the sides; but exactly such recreational riddles served as basis for the new discipline.

If we now consider Chapter VIII of theNineChaptersin its integrity, the parallel becomes obvious. Although theNineChapterson the whole teach administrators’ mathematics, Chapter VIII does not present us with a single instance of this. True,theentitiesthat occur would again (mostly) be of the kind dealt with by calculating bureaucrats (the combined ropes hardly); buttheproblemswould never turn up in their offices. Moreover, the book as a whole is a theoretical unity. Since the topic is absent from theSunshùshū(Cullen 2004: 6;id. 2007: 29; Dauben 2008: 97, 131), Chapter VIII can be assumed to be the outcome of recent systematic establishment of a well-defined mathematical field-inspired in all likelihood by select recreational problems as received within the existing mathematical culture, with its techniques, approaches and metamathematical ideals; administrative mathematicspersewould not lend itself adequately to that role.

All in all, Chapter VIII and its Mediterranean kin thus appears to present us with all the facets involved in questions about transmission:

1.Transmission ofproblemsas riddles from an unidentifiedsomewhereto both the classical Mediterranean area and Han China (and other locations).*Somewheremust be emphasized. In questions of this kind it is misleading to take for granted that the ultimate source must be one of the literate, “nationally” defined high cultures we know about-“the Chinese”, “the Greeks”, “the Indians”, etc. “Proletarians have no fatherland”, it was claimed-until the experience of the First World War proved the opposite in France and Germany. Often, merchants and technicians (even highly qualified techniciansla Wernher von Braun) still have none.

2.Local creation of adequatemethods.

3.A creation of a mathematicaldisciplineon this foundation in China, in a process that is parallel to what can be seen in Old Babylonian mathematics. This parallel was based on shared sociological conditions and certainly did not involve any kind of transmission of metamathematical ideals.*Those of the Old Babylonian school had died with the school itself around 1600 BCE, more or less at the time of the earliest oracle bones. Even if that had not been the case, however, transmission could be safely excluded-institutional ideals can only be exportedwithunderstanding(whence with efficiency) if the institution itself is exported.

Problems about “combined works” present themselves easily in all cultures of scribal mathematical administration, and there are basically only two reasonable ways to solve them;*IfAcan complete the task in 3 days andBin four, then each dayAcompletes 1/3 andB1/4, etc. Alternatively, in 3×4 days,Awill complete it 4 times, andB3 times, the two together thus 7 times, etc. If the numbers had not been mutually prime, the latter method can be found in the variant that the smallest common multiple is chosen, but apart from that sources I have looked at know no other ways. Obviously they are algebraically equivalent.neither the occurrence of such problems in different places nor a shared way to proceed can thus be taken as evidence of transmission. An unlikely dress can, however (as in the case of the “hundred fowls”).

Such a case is present in Chapter VI, problem 6 of theNineChapters(Chemla & Guo 2004: 541). Here, a pool is filled from five streams. As it is, filling is a preferred dress for such problems in theGreekAnthologyXIV-thus no. 7, 130-133, 135(Paton 1916: V, 31, 97, 99). Shared transmission from somewhere is thus likely-but since this is nofavouritedress of the problem type in theNineChapters(other instances-no. 22, 23 and 25-really concern working rates), an isolated borrowed recreational problem may simply have been inserted in an adequate place of theNineChapters, the writer having recognized an already familiar type.*No. 21 and 22 are in the dress of travel times, which also shows up elsewhere in later times. No. 27 and 28, of structure “box problems”, are in the dress of repeated taxation, also familiar from India and elsewhere in the later first and early second millennium. Chapter VI thus serves, it seems, as a receptacle for several widely circulating recreational problems for which it presents the earliest written evidence (much as Diophantos’sArithmeticaI).

All of these cases of credible transmission, from the “hundred fowls” onward, are number problems; they are of the kind that would allow an accountant or a travelling merchant to show his mathematical proficiency. Since accountants are likely to stay more or less in their place, travelling merchants constitute the plausible carrying community for these riddles; at an earlier occasion (Høyrup 1990: 74)I have spoken of them as the “Silk Route group”.

Seleucid and Demotic Geometry

We started with a suggestive geometric diagram, and then shifted focus to the possible transmission of arithmetical riddles. Let us return to geometry.

Our initial diagram is too isolated to be worth pursuing. More intriguing is the geometry of Chapter IX of theNineChaptersin relation to certain geometric problems from Seleucid Mesopotamia (third to second century BCE) and Hellenistic-Demotic Egypt.

The Seleucid problems in question (mainly) deal with rectangles with a diagonal. They have a family relationship with the Old Babylonian so-called “algebra”-apparently not by direct descent but via shared borrowing from the riddles of practical surveyors.*The evidence for this is in part linguistic, in part it has to do with strong reduction (followed by expansion) at the level of mathematical substance. See (Høyrup 2002a: 389-399).The kinship does not imply that the Seleucid problems represent an “algebra”. Whether the Old Babylonian technique does so is a matter of how we define algebra, but no reasonable definition will cover the Seleucid rectangle problems-they do not serve any kind of representation, and the method is purely synthetic.

Most of the problems in question are known from the tablet BM 34568,*(Neugebauer 1935: III, 14-19), partial edition, “conformal” translation and commentary in (Høyrup 2002a: 392-399).undated but probably from the later third or earlier second century BCE. Its problems can be described as follows:*lstands for the length,wfor the width,dfor the diagonal andAfor the area of a rectangle. The sexagesimal place value numbers are transcribed into Arabic numerals. Entities that are found but not named in the text are identified in 〈 〉. With minor changes, I draw the list from (Høyrup 2002b: 13f).

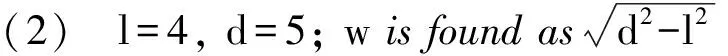
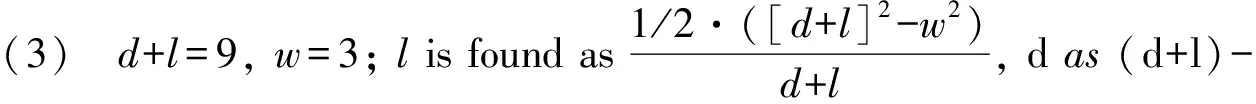
(4) d+w=8, l=4;solutioncorrespondingto(3).

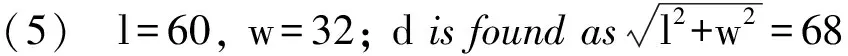
(6) l=60, w=32; Aisfoundasl·w.

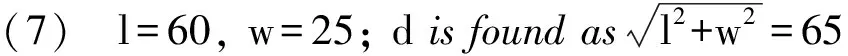
(8) l=60, w=25; Aisfoundasl·w.

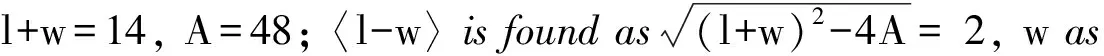
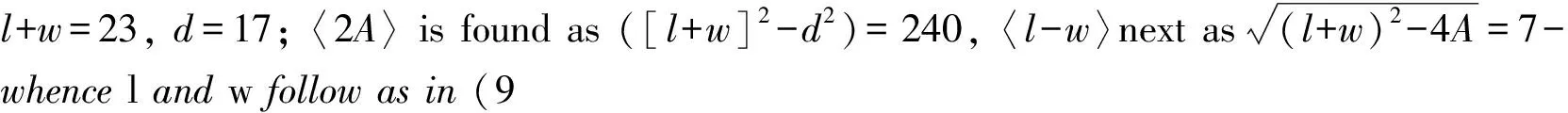
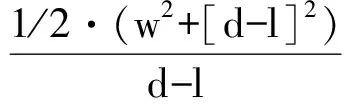
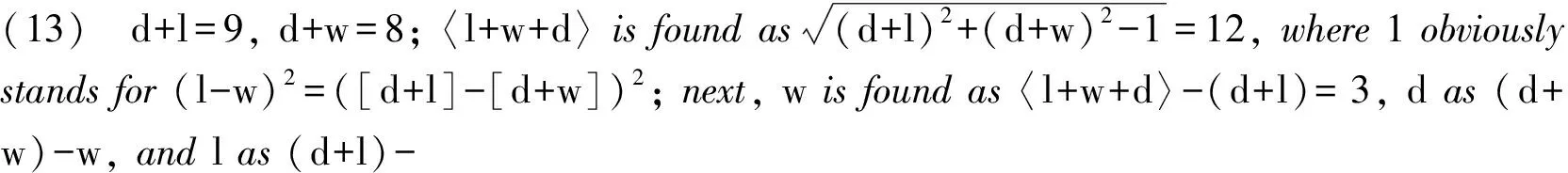
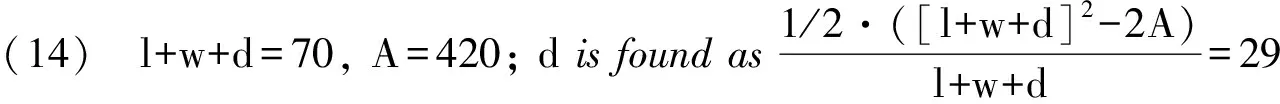
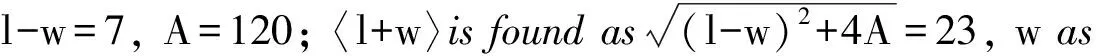
(16) A cup weighing 1 mina is composed of gold and copper in ratio 1:9.*Obviously an intruder, which however shows that at least some problems from the “Silk Road group” were already known in Mesopotamia at the time. In the present context there is no reason to discuss this connection in depth.Similar connectionsmaybe in play in the seemingly aberrant problem 1, extensively discussed, but with a different aim, in (Gonçalves 2008).

(17)l+w+d=12,A=12; solved as (14),d=5.

(18)l+w+d=60,A=300; not followed by a solution but by a rule formulated in general terms and cor-responding to (14) and (17).

(19)l+d=45,w+d=40; again, a general rule is given which follows (13).

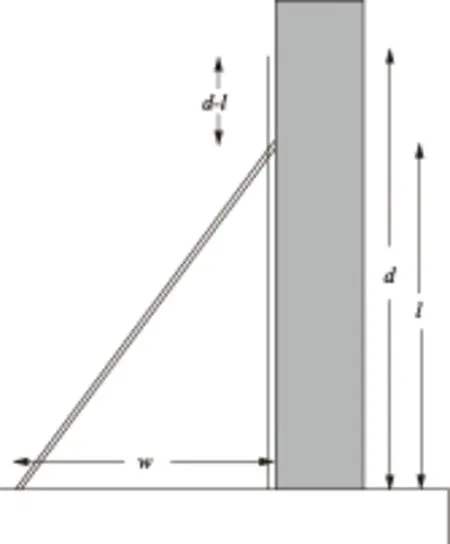
Fig.2 The reed leaned against the wall.

No. 2 is obviously an application of what I prefer to call the “Pythagorean rule”, no theorem being involved; it corresponds to knowledge that was amply around in Old Babylonian times. No. 10 is not identical with the Old Babylonian problem which I referred to initially (Db2-146); but it is closely related and solvable by means of the same diagram.

All the others (disregarding here and in what follows the intruders no. 1 and no. 16) represent innovations within the surveyor’s riddle tradition-when not in question then in method (no. 6 and 8 obviously present old knowledge, which however had been taught at an elementary level). No. 12 deserves particular discussion. It deals with a reed of lengthdfirst standing vertically against a wall, next in a slanted position, in which the top descends to heightl(descending thusd-l); at the same time, the foot moves a distancewaway from the wall.

In the Old Babylonian text BM 85196 we find a similar dress, but theredandware given. To findlthus requires nothing but direct application of the Pythagorean rule (similarly to no. 2 here). In the present case, instead, as stated, the descentd-lis given together withw.

It is possible to find plausible geometric explanations of the procedures used to solve all the “new” problems-see (Høyrup 2002b: 13- 18); that, however, is of no interest in the present connection (in particular, of course, because we have no certainty that these explanations were those which the ancient calculators thought of).

BM 34568 is not our only source for this kind of rectangle problems. Firstly, the Seleucid text AO 6484*Ed. (Neugebauer 1935: I, 96-99); early second century BCE.contains a rectangle problem of the same type as nos. 14, 17 and 18 of BM 34568. Secondly, the Demotic papyrus P. Cairo J.E. 89127-30, 89137-43 from the third century BCE*(Parker 1972: 13-53), with summaryibid. pp. 3f.contains eight problems about the reed leaned against the wall-three of the easy Old Babylonian type wheredandware given, three of the equally simple type wheredandd-l(and therefore easilyl) are given; and two, finally, whered-landware given, as in BM 34568 no. 12. Though with different numerical parameters, moreover, two of its problems coincide with that of the Old Babylonian text Db2- 146; they are thus closely related to BM 34568 no. 10.

There can be no doubt that the ultimate source for this whole cluster of geometric problems is Mesopotamia or at least West Asia-Pharaonic mathematics contains nothing similar. It is also easy to pinpoint a professional community that could transmit it: For half a millennium, Assyrian, Persian and Macedonian military surveyors and tax collectors (even those of the Macedonians no doubt trained in the Near Eastern tradition) had walked up and down Egypt.*Macedonians excepted, this explains why Greek authors, from Herodotos onward, could believe the Egyptians to have invented geometric techniques which we now recognize as Mesopotamian.

Travelling geometry-travelling how far？

It is less easy to identify the channels through which these problems came to be adopted into Jaina mathematics, as they certainly were (Høyrup 2004). Our evidence is constituted by Mahvīra’sGanita-sāra-sangrahafrom the ninth century CE, but it is obvious from Mahvīra’s words that by then these problems were considered old, native and venerable by the Jainas. It is also highly plausible that what reached them had already been digested and somewhat transformed by a broader Mediterranean community.

Given that they reached India, could they also have inspired China’s mathematical bureaucrats, or at least the author of Chapter IX of theNineChapters(which has no more to do with real administrative tasks than Chapter VIII)？

At a first glance, problems 6 to 12 and 24 might suggest so. In that case, however, the inspiration has certainly been digested-the basic topic of Chapter IX is the righttriangle, and the Seleucid-Demotic problems deal with rectangles.*Problem 11 in theNineChaptersthenappliesthe triangle techniques to a problem about a rectangular door, while the Seleucid text applies its rectangle techniques to the slanted pole, a triangle problem. Both writers obviously understood the connection, but their choice of different basic models is still to be taken note of.Moreover, the Chinese variant of the reed against the wall (no. 8-the only one where the dress is suggestive) compares the slanted and thehorizontalposition of a pole.

If we express the Chinese problems in the same symbolic form as used for BM 34568, we get the following:*Once more I borrow (this time more freely) from (Høyrup 2002b).

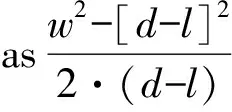
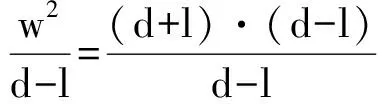
(8)d-l=1,w=10. Same mathematical structure and same procedure as no. 7-but the dress is now a pole first leaning against a wall and then sliding down to horizontal position.

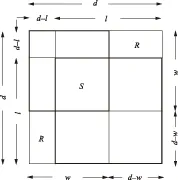
Fig.3 The possible geometric basis for problem IX.24 of the Nine Chapters.

(9) Another variation of no. 7.

(10) Yet another variation of no. 7.

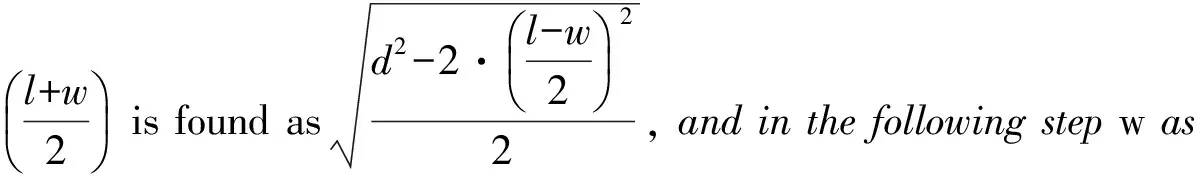
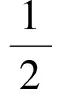
All in all, the similarities boil down to the mathematical structures underlyingthequestions. The dresses are generally quite different, and the procedures used to obtain the solutions are also others, often as different in character as the subject allows. In summary, no decisive internal evidence speaks in favour of transmission-only problem 7couldbe an accidental intruder that has been inserted in the adequate place, as the filling problem 6 in Chapter VI.

External evidence also seems unfavourable to the transmission thesis: arithmetical riddles might be carried along the Silk Road network by travelling merchants and exchanged as camp fire fun or challenges. But where can we find likely carriers of geometrical questions？

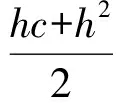
There is a fundamental difference, however. In this case the formula has travelled together with the problem to which it is linked. If diffusion should be involved in the problems of Chapter IX, all that was transmitted was the mathematical structure of the problems, neither the actual questions to which they correspond nor the formulas used to solve them. This could only be carried by people who would recognize as essential an abstract mathematical structure behind the problems-that is, by people who must be characterized asmathematicians. They were hardly at hand for the task.

All in all, Chapter IX of theNineChapters(of which problems 6-13+24 only form a subset) is therefore likely to be just as much an original Han creation as Chapter VIII-but with the difference that the underlying inspiration must be sought in local geometric practice, and not in the practice or riddles of any transnational professional community. TheGnomonoftheZhou, on which Zhao Shuang was certainly not the first to work, would suggests the practice of astral science. Since Chinese astral science is a field about which I am quite ignorant, I shall not pursue this suggestion, which is anyhow outside my topic.

Boncompagni, Baldassare (ed.), 1857.Scrittidi Leonardo Pisano matematico del secolo decimoterzo. I. IlLiberabbacidi Leonardo Pisano. Roma: Tipografia delle Scienze Matematiche e Fisiche.

Chemla, Karine, & Guo Shuchun (eds., trans.), 2004.Lesneufchapitres.LeClassiquemathématiquedelaChineancienneetsescommentaires. Paris: Dunod.

Christianidis, Jean, 1994. “On the History of Indeterminate Problems of the First Degree in Greek mathematics”, pp. 237-247inKostas Gavroglu, Jean Christianidis & Efthymios Nicolaidis (eds.),TrendsintheHistoriographyofScience. Dordrecht: Kluwer.

Cullen, Christopher, 1996.AstronomyandMathematicsinAncientChina:TheZhou bi suanjing. Cambridge: Cambridge University Press.

Cullen, Christopher, 2004. TheSunshùshū, “Writings on Reckoning”: A Translation of a Chinese Mathematical Collection of the Second Century BC, with Explanatory Commentary. (Needham Research Institute Working Papers, 1). Cambridge: Needham Research Institute. Web Edition http://www.nri.org.uk/suanshushu.html.

Cullen, Christopher, 2007. “TheSunshùshū, ‘Writings on Reckoning’: Rewriting the History of Early Chinese Mathematics in the Light of an Excavated manuscript”.HistoriaMathematica, 34, 10-44.

Dauben, Joseph W., 2008. “SuanShuShu.ABookonNumbersandComputations.English Translation with Commentary”.ArchiveforHistoryofExactSciences, 62, 91-178, erratum p. 347.

Folkerts, Menso(ed.), 1978. “Die älteste mathematische Aufgabensammlung in lateinischer Sprache: Die Alkuin zugeschriebenenPropositionesadacuendosiuvenes”. ÖsterreichischeAkademiederWissenschaften,Mathematisch-NaturwissenschaftlicheKlasse.Denkschriften, 116. Band, 6. Abhandlung.

Hermelink, Heinrich, 1978. “Arabic Recreational Mathematics as a Mirror of Age-Old Cultural Relations Between Eastern and Western Civilizations”, pp. 44-52inAhmad Y. Hassan, Ghada Karmi & NizarNamnum (eds),ProceedingsoftheFirstInternationalSymposiumfortheHistoryofArabicScience,April5-12, 1976. Vol. II,PapersinEuropeanLanguages. Aleppo: Institute for the History of Arabic Science, Aleppo University.

Høyrup, Jens, 1990. “Sub-Scientific Mathematics.Observations on a Pre-Modern Phenomenon”.HistoryofScience,28, 63-86.

Høyrup, Jens, 2001. “On a Collection of Geometrical Riddles and Their Role in the Shaping of Four to Six‘Algebras’”.ScienceinContext,14, 85-131.

Høyrup, Jens, 2002a.Lengths,Widths,Surfaces:APortraitofOldBabylonianAlgebraandItsKin. New York: Springer.

Høyrup, Jens, 2002b. “Seleucid Innovations in the Babylonian ‘Algebraic’ Tradition and Their Kin Abroad”, pp. 9-29inYvonne Dold-Samplonius et al (eds),FromChinatoParis: 2000YearsTransmissionofMathematicalIdeas. (Boethius, 46). Stuttgart: Steiner.

Libbrecht, Ulrich, 1974. “Indeterminate Analysis: Historical Relations between China, India, Islam and Europe”, pp. 311-314inXIVthInternationalCongressoftheHistoryofScience,ProceedingsNo. 3. Tokyo & Kyoto: Science Council of Japan.

Needham, Joseph, 1959.ScienceandCivilisationinChina. III.MathematicsandtheSciencesoftheHeavenandtheEarth. Cambridge: Cambridge University Press.

Neugebauer, Otto (ed.,trans.), 1935.MathematischeKeilschrift-Texte. I-III. (Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik. Abteilung A: Quellen. 3. Band, erster-dritter Teil). Berlin: Julius Springer, 1935, 1935, 1937.

Parker, Richard A. (ed.,trans.), 1972.DemoticMathematicalPapyri. Providence & London: Brown University Press.Paton, W. R. (ed., trans.), 1916.TheGreekAnthology.5 vols. New York: G. P. Putnam / London: Heinemann, 1916-1918.

Schöne, Hermann (ed., trans.), 1903. Herons von AlexandriaVermessungslehreundDioptra. Griechisch und deutsch. Leipzig: Teubner.

Shorey, Paul (ed., trans.), 1930. Plato,TheRepublic. 2 vols. London: Heinemann / New York: Putnam, 1930, 1935.

Suter, Heinrich, 1910. “Das Buch der Seltenheiten der Rechenkunst von Abū Kmilrī”.BibliothecaMathematica, 3.Folge 11, 100-120.

Tannery, Paul (ed., trans.), 1893.Diophanti AlexandriniOperaomniacum graecis commentariis. 2 vols. Leipzig: Teubner, 1893-1895.

van Hée, Louis, 1913. “Les cent volailles ou l’analyse indéterminée en Chine”.T’oungPao, 14, 203-210, 435-450.

Vogel, Kurt, 1983. “Ein Vermessungsproblem reist von China nach Paris”.HistoriaMathematica, 10, 360-367.

Winter, John Garrett (ed.), 1936.MichiganPapyri. Vol. III.MiscellaneousPapyri. Ann Arbor: University of Michigan Press.

塞琉西、古埃及、地中海数学与《九章算术》之“方程”和“勾股”：偶然亦或显著相似？

简斯·休儒

(罗斯基尔德大学)

几何图示与算术结构的相似性,往往被作为中国与“西方”之间开展数学知识与方法交流的证据。比对《九章算术》第八章“方程”中某些问题与源自古希腊的相似问题,第九章即关于直角三角形的“勾股”部分与塞琉西的一部关于矩形的问题集,得出如下两点结论：(1)关于一些算术难题(但不含解法)的交流很可能存在——并非“来自希腊”,而是来自商贾们的跨国团体,这些算题激发了中国“方程”解法的创生,《九章算术》第八章就是其系统阐述；(2)相反,关于几何问题的交流则不太可能(除了一个可能的例外),《九章算术》第九章“勾股”的系统阐述乃是基于本土的几何学实践之上。

《九章算术》 方程 交流 数学难题 巴比伦几何学

N091∶O11

A Article ID 1000- 0224(2016)04- 0463- 14