王淑红 邓明立

(河北师范大学数学与信息科学学院,石家庄 050024)

爱米·诺特对交换环论的贡献

王淑红 邓明立

(河北师范大学数学与信息科学学院,石家庄 050024)

抽象代数是数学的重要分支,主要研究群、环、域、模、格等数学结构。环论是抽象代数中较为深刻的一部分,按照乘法是否满足交换律,环可以划分为交换环和非交换环两大类。在详尽占有并阅读原始文献和研究文献的基础之上,分析了爱米·诺特为何从不变量论转到交换环论的研究,并且揭示了爱米·诺特通过对升链条件的重视与应用,完成对抽象环,特别是诺特环的公理刻画,从而建立起抽象交换环论,并促使抽象代数学这门学科正式建立起来。

环 交换环 升链条件 爱米·诺特

抽象代数是数学的重要分支,主要研究群、域、环、模、格等数学结构。环是抽象代数中较为深刻的一部分,正如著名代数学家林节玄(T. Y. Lam)在其1991年出版的著作《非交换环初级教程》(AFirstCourseinNoncommutativeRings)[1]的序言中所说：“如今,环论是群论(群环)、表示论(模)、泛函分析(算子代数)、李理论(包络代数)、代数几何(有限生成代数、微分算子、不变量理论)、算法(序、布饶尔群)、泛代数(环簇)和同调代数(环的上同调、投射模、格罗滕迪克及高阶K-群)的一个丰饶的交汇地带。”环对于乘法并不一定都满足交换律和结合律,由此得到结合环与非结合环。结合环主要包括复数、四元数、超复数拓广而来的结合代数,线性方程组、行列式发展而来的矩阵,以及群表示论发展而来的群代数。非结合环主要包括源于八元数、双四元数的交错代数,李变换群、李代数发展而来的李环,以及由量子力学所产生的若尔当代数。按照乘法满足交换律与否,可将环划分为交换环和非交换环两大类。交换环和非交换环虽皆源于19世纪早期,但其起源和发展路径并不相同。交换环理论起源于代数数论、代数几何和不变量理论,反过来,亦主要应用于这些领域。克莱纳(I. Kleiner)在“从数到环：环论的早期历史”(Fromnumberstorings:theearlyhistoryofringtheory)一文中给出了下面的环论发展脉络图(图1)([2],19页)。

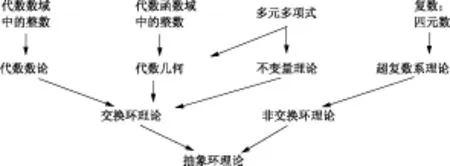
图1 克莱纳环论发展脉络图

目前,国内外对环论的历史研究主要有：1930～1931年范德瓦尔登(B. L. Van der Waerden,1903～1996)两卷本的《近世代数学》,基本囊括了此前抽象代数学的成果,宣告了抽象代数学的诞生,随即抽象代数学就被引入到代数几何学领域,导致了代数结构的广泛采用。他详细地论述了抽象代数学的发展历史,为环论的历史研究提供了框架和线索[3]。凯瑞(L. Corry)研究了现代代数及其数学结构的起源,他以19、20世纪的数学观念的发展为向导,以理想这一环论中的核心概念为实例,对现代数学结构的起源和发展有很高理论层次的剖析。他还从美国的归纳分析出发,对p进数理论、抽象域理论、弗兰克尔(A. Fraenkel,1891～1965)对p进系的公理化以及弗兰克尔之后的理想与环进行了深刻阐述[4- 5]。克莱纳除系统论述了群、环、域等代数结构的发展历史之外,还着眼于爱米·诺特(E. Noether,1882～1935,以下简称诺特)对交换和非交换代数以及表示论的影响,为环论的历史研究提供了很好的历史框架。他还对抽象环的概念来源进行了有理有据的分析[2,6,7]。古德斯坦(C. Goldstein)等人研究了自高斯(C. F. Gauss,1777～1855)开始的数论发展史,为环论在数论中的起源提供了重要的思想[8]。格瑞(J. J. Gray)和帕舍尔(K. H. Parshall)介绍了1800至1950年的代数学历史,其中包括符号运算、代数教材、代数数论、线性代数、早期的交换代数、域论和代数几何中的抽象代数方法[9]。爱德华(H. M. Edwards)对库默尔(E. E. Kummer,1810～1893)、戴德金(R. Dedekind,1831～1916)、克罗内克(L. Kronecker,1823～1891)等人及其关于理想、环以及数学观念的系列论文,是对环论相关概念和背景的深入探析[10- 14]。吉姆柏林(C. Kimberling)等对诺特及其理想、环论的贡献进行了评述[15]。国内诸如《20世纪数学思想》、《近代数学史》、《数学史概论》、《中国近代代数史简编》、《代数数论简史》、《世界数学通史》这样一些学术著作中多多少少涉猎一些环论相关的内容,再加上此前笔者在这方面的研究积累,本文试图对诺特在交换环论方面的贡献进行较为系统的剖析。

1 有史以来最杰出的女数学家爱米·诺特

作为历史上最杰出的女数学家,诺特对数学和理论物理都曾做出重要成就。她在物理上关于对称性和守恒定律之间关系的结果,十分关键而优美,被称为诺特定理,是现代物理基础的重要组成部分[16]。数学方面,诺特的工作主要可以划分为4期：不变量理论时期(1907～1919)、交换代数时期(1920～1929)、非交换代数和表示论时期(1927～1933)以及非交换代数在交换代数中的应用时期(1932～1935)[6]。由此可以看出,她在不同方面的工作是有交叠的。她这几期的工作都是卓有成效的,特别是把当时新兴的代数学领域发展成为了众所周知的抽象代数学。

其实,诺特在不变量理论方面的工作就已经使她跻身一流数学家的行列。那么她为什么从不变量理论转而研究交换代数呢？这要从她的家庭谈起。诺特1882年3月23日生于德国爱尔朗根的一个犹太家庭,其父马克思·诺特(M. Noether,1844～1921)自1875年起到1921年辞世前,始终在爱尔朗根大学任教授,是一位颇有建树的数学家,主要研究代数几何,而且在代数几何的研究中对属于交换代数的多项式理想论做出了贡献,这势必成为影响诺特研究的一个因素。此外,有不变量之王之称的戈丹(P. Gordan,1837～1912)与其父是亲密的朋友,是她家的座上宾。在此影响下,诺特对数学萌生了浓厚的兴趣。事实上,诺特后来成为了戈丹的学生,在戈丹的指导下做博士论文。1903年冬天,诺特到哥廷根大学,度过了一个学期。聆听了克莱因(F. Klein,1849～1925)、希尔伯特(D. Hilbert,1862～1943)和闵可夫斯基(H. Minkowski,1864～1909)等数学家的课程,开阔了视野,受到了鼓舞,于是更加坚定了研究数学的决心。1907年12月,诺特以十分优秀的成绩顺利通过博士考试,成为有史以来第一位女性数学博士。其实,在此期间,她深受费舍尔(E. Fischer,1875～1959)的影响,而费舍尔遵循的是希尔伯特的方法。因此,在费舍尔的指导下,她从戈丹的风格转向希尔伯特的抽象风格,从而最终建立了抽象环论[17- 20]。

1932年,诺特获得两项重大荣誉。第一项是,她与阿廷(E. Artin,1898～1962)因数学成就共同获得的阿克曼·特布纳纪念奖(Ackermann-TeubnerMemorialPrize)。另一项是,她应邀在苏黎世举办的第九届国际数学家大会上做了1小时的大会报告。

2 交换环论正式诞生的前奏

交换环论主要起源于代数数论、代数几何和不变量理论,反过来,亦主要应用于这些领域。对这些领域的发展尤为重要的是代数数域和代数函数域中的整数环以及二元和多元多项式环[2]。交换环理论可以追溯到高斯,1832年,高斯为解决高次互反律问题引进后人所称的复整数或高斯整数,从现代的数学观点来看,全部复整数构成的集合就是复整数环。之后,出现了二次代数整数环和分圆整数环。唯一因子分解问题是这些环中的主要问题,是解决高次互反律问题的关键。库默尔在上述基础上引进理想数,实现了唯一因子分解,不但解决了高次互反律问题,而且使得费马大定理的解决迈出了关键性的一步。1871年,戴德金引进理想,理想成为一种集合和计算对象,是代数整数环中的特殊的子环,这标志了理想理论的诞生。他还给出一个相当于环的新概念序环。另外,克罗内克几乎同时也把相当于代数整数环的集合称为序环,在其上建立了除子理论。这些构成了一维交换代数的基础,而高维交换代数的基础则是代数几何,特别是希尔伯特证明的基定理和零点定理。拉斯克尔(E. Lasker,1868～1941)在1905年引进准素理想概念,提出准素分解。1913年麦考莱(F. S. Macaulay,1862～1937)曾考虑分解的唯一性问题。这时,交换环理论还是具体的：一方面是复数域上的多项式环及其理想理论,另一方面还没有从域的概念中摆脱出来成为环的理论。

总之,在20世纪的前10年,已经建立了具体的交换环、非交换环及理想理论。此前,群、域以及向量空间的抽象公理化定义已经成形,抽象环的定义还在酝酿之中。1914年,由具体环向抽象环的过渡迈出了重要一步,弗兰克尔在“论零因子和环的分解”(überdieTeilerderNullunddieZerlegungvonRingen)一文中给出环的第一个抽象定义[21]。不过,需要说明的是,弗兰克尔给出的环定义与现在通用的环定义并不相同。([17],133页)有关弗兰克尔对抽象环定义的背景历史材料可参考文献[5]。当今通用的交换环的定义最先出现在园正造(M. Sono,1886～1969)1917年的文章“论同余”(OnCongruences)中[22]。克莱纳曾对此评述道：“园正造的文章是非常现代、抽象的作品,讨论陪集、商环、极大极小理想、单环、同构定理以及合成列。”([2],33页)自此,环不再局限于多项式环、代数整数环和超复数环等具体的环,而成为独立的抽象研究对象。但尽管如此,具体的环仍然在环论中占有重要地位,而摆脱具体限制真正迈入抽象交换环理论的是诺特。

1920年,诺特开始对代数学产生兴趣,并开展研究工作,很快成为哥廷根大学的领袖数学家,吸引全世界的年轻数学才俊环绕其周围,并形成了著名的哥廷根大学代数学派。

抽象代数学中有一个重要的概念,称为诺特环,是抽象代数当中的满足升链条件的一类环。是希尔伯特在研究不变式论的时候,首次证明了多项式环的每个理想均为有限生成的,之后诺特在里面精炼出升链条件,这就是诺特环名字的由来。诺特环这个名字最早出现在谢瓦莱(C. Chevalley,1909～1984)1943年在《数学年刊》上发表的论文“关于局部环理论”(Onthetheoryoflocalrings)中。([17],133页)

数学上,若任意偏序集p的元素的升链a1≤a2≤…最终固定,就是说存在正整数n,使得对所有m>n,有am=an,则说p适合升链条件。类似地,若任意偏序集p的元素的降链a1≥a2≥…最终固定(就是说不存在无穷降链),则说p适合降链条件。

1920年,诺特与施梅迪勒(W. Schmeidler,1890～1969)共同发表一篇论文研究微分算子[23]。在数学当中,顾名思义,微分算子就是定义为微分运算的函数的算子。这篇文章主要研究微分算子的定义域、理想的剩余类和群及其相互关系。认为：得出其内在关系的基本工具为同构的思想。依靠微分算子与多项式的相似性,研究其因子分解性质[4]。这一篇文章可以看作是诺特抽象结构方法的前奏。随后她分别于1921和1927年发表两篇重要论文,实现了交换环论的抽象结构化。

3 交换环论的正式诞生——诺特的标志性贡献

实际上,诺特是在前人大量工作的基础上取得关键进展的。我们前面已经阐述了高斯、库默尔、戴德金、克罗内克、马克思·诺特、希尔伯特、拉斯克尔、麦考莱等一流数学家的成果。数学是一个积累的过程,积累到一定程度就会有一个大的爆发。诺特使得交换环论变成了强大的抽象理论。

诺特于1921年和1927的两篇开创性论文可以追溯到代数几何和代数数论。1921年发表的论文题目为“环中的理想论”(IdealtheorieinRingbereichen)[24],1927年发表的论文题目为“代数数域和代数函数域上理想论的抽象结果”(AbstrakterAufbauderIdealtheorieinalgebraischenZahl-undFunktionskörper)[25]。在文献[17]中,有吉尔摩(R. Gilmore)写的“交换环论”(commutativeringtheory)一文,其中谈到了诺特的论文写作风格*作者在这里特别感谢审稿专家建议补充诺特论文写作风格的说明并热诚地提供文献[17]中的英文资料!。他在分别具体讨论诺特的上述两篇文章之前,对二者进行了一般性评述：

在某种程度上,我们提到的这些方面可能是一个时代的反映。在那时,对期刊的空间要求并不多,印刷费用也不是决定一篇刊出论文怎样表述的重要因素。这两篇论文的步调悠闲,但绝非懒散；它们大约有25篇参考文献,但每一篇基本上都是独立的。对于一个有合理知识基础的读者,证明足够详尽,不会太令人头痛。与在那时发表的论文的通常做法一样,脚注非常多——“理想论”中有51个,“结果”中有34个。参考文献和例子经常被放在脚注中。同样,结果的成因、类似方法或思考的文献以及理论的局限性也被放在脚注中。“理想论”和“结果”的脚注比正文更能体现诺特的某些个性特征——慷慨地给予别人赞扬、对自己的贡献的重要性相对来说谦逊、充分了解和推崇戴德金的工作。总之,这些文章读起来给人一种愉悦感,而且它们似乎比如今发表的代表性文章更具直觉、洞察力和动机。([17],132页)

3.1 “环中的理想论”

19世纪,代数学主要研究实数或复数域上的多项式环k[x1,x2,…,xn],其中k是一个域。多项式环的研究在19世纪末和20世纪初取得进展,希尔伯特、拉斯克尔和麦考莱证明,在多项式环中每一个理想都是准素理想的有限交,且具有唯一性。如果用几何的语言,就是说每一个簇都是不可约簇的唯一有限交。

诺特在论文“环中的理想论”中,将这个结果推广到具有升链条件的任意交换环,并得到在这样的环中每一个理想都是准素理想的有限交,且具有唯一性。她将唯一因子分解理论从多项式环、代数数域以及代数函数域的整环扩展并抽象,得出带有升链条件的抽象的交换环,现在称之为诺特环。

现在,一个环A称为诺特环,当且仅当对于每一个由A的理想所组成的升链a1⊂a2⊂…⊂an⊂…,必存在n,m属于N,使得对所有的n,m≥N,都有an=am。[26]

弗兰克尔没有用理想建立起环和因子分解问题之间的相互关系,而诺特首先给出了它们的联系。因为当时许多数学家还对环的概念很陌生,所以诺特在文章中证明了环的最基本性质。

实际上,诺特在论文的一开始就清楚地说明了文章的目的。她这样写道：

这篇文章的目标为,把有理整数的因子分解定理以及代数数域上理想的因子分解定理推广到任意整环以及一般环的理想上。([24],25页)

她在这篇文章中阐述了4个因子分解定理,开始研究环的抽象结构,并逐渐得到了数学家们的一致认可。她把交换环的理想的升链条件纳入进来,并且给出了这些环存在基本分解的证明。在交换代数当中,准素分解能够把一个交换环的理想或者模唯一地表示为准素理想或者准素子模之交。这个结果可以说是算术基本定理的推广,可以用来研究代数几何的课题。

拉斯克尔在1905年在文章“模与理想论”(ZurTheoriederModulnundIdeale)中证明了这个结论对于R为多项式环的情形成立[27],而诺特在“环中的理想论”中证明了这个推广形式。因此,准素分解的存在性也一向称为拉斯克尔-诺特定理。

她借鉴戴德金的方法,用“由一个数生成的理想”来代替“数”,得到代数数域上的关于理想的定理。她借鉴弗兰克尔的思想,定义了抽象环。她认为弗兰克尔所给出的环的定义,有一些不必要的限制条件。她主要研究了满足有限性条件(Endlichkeitbedingung)的交换环(一般而言没有单位元),即每个理想都有一个有限基的环。她证明了,有限性条件和升链条件等价。戴德金和拉斯克尔之前已经证实和使用过具体的升链条件,而诺特把升链条件重视起来,这是一个重要转变。

总之,诺特在“环中的理想论”中引入了抽象代数学的环、模、理想和升链条件等基本概念,并使得这些概念处于显著地位,还综合运用了抽象方法、公理方法和概念性方法。事实上,戴德金曾提出和研究过这些概念,因此诺特一向推崇戴德金是有道理的。诺特负责编辑戴德金的全集,受到戴德金的影响也是自然的。

当然,诺特在“环中的理想论”中主要关注的问题还是唯一因子分解问题。根据范德瓦尔登的评价,这篇文章表明,把希尔伯特的方法应用于多项式理论是很成功的,因为它包含着仅以有限性条件为基础的拉斯克尔定理的一个证明。诺特的工作表明,这个定理对所有这样的环都成立,因为环里的每个理想都有一个有限基[5,7]。抽象环里对因子分解问题的进一步公理化是诺特本人在1926年完成、1927年发表的。

1927年,诺特发表“代数数域和代数函数域上理想论的抽象结果”。她在更为严密的抽象公理化背景下,讨论了将理想表示成代数数域和代数函数域的整环中唯一素理想乘积,阐释了其中每一个非零理想均可以唯一表示成素理想的乘积的抽象交换环,这种环现在称为戴德金环。

四是现有粮食管理系统仍然可以正常运行。当前，国家粮食局是负责全国粮食流通宏观调控具体业务、行业指导和中央储备粮行政管理的行政机构。如果将大豆(与薯类)从原口径中分列出来，可能会影响粮食局职能部门的一些业务调整，但并不会改变现有粮食局系统的职权范围。而且，统计口径调整将进一步明晰口粮、饲料用粮与油料概念，有助于精准调控全国口粮、饲料用粮与油料的生产与流通，实现全国的粮食管理从强调“粮食安全”向强调“食物安全”转变，拓宽解决粮食问题的思路。

3.2 “代数数域和代数函数域上理想论的抽象结果”

诺特的论文“代数数域和代数函数域上理想论的抽象结果”主要源于代数数论,也或多或少受代数几何学的影响。那么代数数论和代数几何是如何影响她的这篇论文的呢？

就代数数论的影响而言,代数数论可以追溯到高斯的二次型理论、四次互反律以及费马大定理。而求解或求证这些问题的关键都是代数数域整数环中的唯一因子分解,试图寻找使得唯一因子分解成立的环。戴德金和克罗内克分别用不同的方法找到了这样的环,引入了理想的因子分解。如果R是一个代数数域的整数环,那么R的每一个理想均能够唯一地表示成素理想的乘积。

就代数几何而言,代数几何研究代数曲线以及代数簇。代数曲线相当于是代数函数的根所组成的集合。1882年戴德金和韦伯(H. Weber,1842～1913)用代数的方法阐述了黎曼(G. F. B. Riemann,1826～1866)关于复值函数论的一些思想。戴德金和韦伯把代数数域和代数函数域进行类比,把代数数域中的结果移植到了代数函数域中。戴德金和韦伯还指出了代数数论和代数几何间的相互交叉影响。具体来讲,在代数数论中可以将一个代数数域Q(u)和一个给定的代数数u联系起来,在代数几何中也可以将一个代数函数域C(x,y)和一个给定的代数函数联系起来。C(x,y)由变量为x和y的复系数多项式构成,其中y满足系数在C(x,y)中的一个多项式方程,也就是说,y是C(x)上的代数元素。如果A是C(x,y)的整数环,也就是说,A由系数在C(x)中,首项系数为1的多项式C(x,y)的根构成,那么戴德金和韦伯的论文中的一个主要结果就是：A中的每一个理想可以唯一地表示为素理想的乘积[6]。以此为基础,诺特在“代数数域和代数函数域上理想论的抽象结果”中将上述代数数域和代数函数域中的分解结果推广到了交换环中。事实上,她刻画了那些每一个理想均能够唯一地表示成素理想乘积的交换环。

她一改在“环中的理想论”中一开始就给出升链条件的风格,从一个交换环R出发,通过引进新公理,证明了一系列分解定理,使得各个公理和定理之间有了更好的衔接。把她在这里引入的5个公理组合起来,就定义了而今的戴德金环。满足环里的每个准素理想是一个素理想的方幂。她证明了R是一个戴德金整环当且仅当

(1)R满足升链条件；

(3)对于环R的乘法,存在一个单位元；

(4)环R里没有零因子；

(5)环R在它的商域当中为整闭的。(也就是说,商域的每个元素对于R是一个整数,它实际上属于R。)

诺特在给出因子分解定理的证明之前,先给出环的一般性的介绍。环是带有两种运算的一个集合。她认为应该在集合上定义相等关系(Gleichheitsrelation)。她的解释与弗兰克尔对于环的处理有些相近。这个相等关系在环的结构里有重要作用。她认为,如果相等的含义不是集合论中的恒等式,那么为使相等可以应用于每个子系统,比如子环、模、理想等,这样的子系统和一个固定元素必须同时包含与它相等的所有元素[25]。

她给出了一些基本概念。选取一个有单位元但无零因子的环T,考虑它的一个包含单位元的固定子环R。一个R-模被定义为T的一个子集,其元素满足R中的加法和乘法。一个理想是它的所有元素都属于R的一个模。R的完全包含在T里的扩张环S称为序。

R-模的理论比起向量空间的线性代数更复杂一些。这个概念最初是由戴德金定义的,表示理想的因子分解定理成立的数的集合；代数整数的集合就是其中一个序。戴德金认为,序是具有一般性的理论,代数整数集合只是其特殊情形。诺特在抽象环中完成了戴德金的设想,她直接把戴德金的思想转换到抽象环及其扩张中。

诺特还论述了有限模,即存在一个有限基的模。诺特证明了定理：

如果R是满足升链条件的有单位元的交换环,M是一个有限的左R-模,那么M也满足升链条件。([25],34页)

这个定理是用结构化的语言来表述和证明的,其证明依赖M的子模的格和R的理想的格之间的某个对应。这个格简洁地表达了这两个域的子域的包含关系。她对任意一个环的模同构定理进行了抽象化。她认为,抽象环不但是一个阐明广义的因子分解定理的好结构,而且越来越成为有内在价值的研究对象。

在确定抽象环论的基础和实现其结构化的过程中,因子分解定理实际上是自然的。与在“环中的理想论”一文中一样,诺特证明了不可约理想是准素理想,这可由升链条件直接推出。她证明了,准素理想是与其相伴的素理想的方幂。她在推论中给出主分解定理：若环R满足上面的5个公理,则R中的每一个理想均能够唯一地表示成有限个素理想的方幂的交。

在论文“代数数域和代数函数域上理想论的抽象结果”中,她还证明了环和模的同态和同构定理,证明了模M有一个合成列当且仅当它满足升链条件和降链条件。诺特也证明了如果R-模M是有限生成的且R满足升链条件或降链条件,则M也满足升链条件或降链条件。实际上,这是证明了双链条件与合成列的等价性。她通过对合成列的长度进行归纳,证明了广义的若尔当-霍尔德定理[4]。

4 爱米·诺特的影响

从纯数学上来讲,诺特没有简单地整合前人的成就,而是证明了许多新定理,发展了许多新理论,帮助建立了即将统治数学许多年的代数学新观念。与域论抽象化的集大成者斯坦尼兹的工作相比,她的工作有更大的整体影响。群论是第一个抽象化的代数学科,域论是第一个从数域的研究中产生并转化为抽象的、结构化对象的代数学科,而抽象环里理想论的研究,则强化了作为一门学科,代数学应该是关于代数结构研究的一门学科。这一门学科的成熟也带动了整个数学的发展。

诺特的影响力之大,我们可以通过一些著名数学家对她的中肯评价来体悟。代数学家卡普兰斯基(I. Kaplansky,1917～2006)把诺特誉为抽象代数学之母。麦克莱恩(S. MacLane,1909～2005)认为抽象代数学作为一门真正的学科,就是从诺特1921年发表的论文“环中的理想论”开始。外尔则认为诺特使得代数学的面貌焕然一新。外尔还认为,诺特的工作对自己在群和量子力学方面的工作非常有益。他曾说：

她对代数学的重要贡献不能完全从她自己的论文中来看。她循循善诱,其许多思想是在她的学生及合作者的工作中体现出来的。[28]

这一评述一点也没错,因为我们已经看到,上面诺特和施梅迪勒的合作就体现了她的思想。范德瓦尔登无疑是受到了诺特的深刻影响,不但是他的《近世代数学》著作,而且他对代数几何的研究同样如此。范德瓦尔登曾说：

1924年,当我来到哥廷根时,展现在我面前的是一个新世界。我从诺特那里获悉,解决我的代数几何问题的工具已经有了……[29]

范德瓦尔登还认为：数、函数和运算之间的关系,从它们的特殊对象分离开来并且表述为普遍适用的概念之后,就变得更加透彻明朗,更可广泛地应用,产生更加丰富的结果。这正是对诺特的思想本质的一个概述。在诺特去世后不久的1935年9月,亚历山德罗夫(P. Alexandrov,1896～1985)发表了纪念诺特的讲话,明确说到他和霍普夫(H. Hopf,1894～1971)合写的著作里的许多重要思想都源于诺特。

诺特所产生的巨大影响还可以通过她在哥廷根的学生的数量和质量一窥究竟。她指导过的博士生有(其中名字前的时间是博士毕业年份)：1911年,法尔肯博(H. Falckenberg,1885～1946)；1916年,赛德尔曼(F. Seidelmann,1890～？)；1925年,赫尔曼(G. Hermann,1901～1984)；1926年,格雷尔(H. Grell,1903～1974)；1927年,多拉特(W. Doräte)；论文未及答辩即亡故,霍尔泽(R. Hölzer,1903～1926)；1929年,韦伯(W. Weber,1906～1975)；1929年,列维茨基(J. Levitski,1904～1956)；1930年,多伊林(M. Deuring,1907～1984)；1931年,费汀(H. Fitting,1906～1938)；1933年,维特(E. Witt,1911～1991)；1933年,曾炯(C. Tsen,1897～1940)；1934年,席林(O. Schilling,1911～1973)；1935年,斯托弗(R. Stauffer,1910～1993)；1935年,沃贝克(W. Vorbeck,1909～？)；1936年,维希曼(W. Wichmann,1912～1944)。这份名单中的曾炯是中国数学家。

除学生外,还有很多围绕在诺特身边的学者和同事,在哥廷根大学形成了以诺特为首的抽象代数学派。2015年3月23日,谷歌为纪念诺特诞辰133周年,专门为其制作了数学涂鸦。这个谷歌数学涂鸦中除了有诺特的照片之外,背景当中有很多与环有关的物件,就是为了纪念诺特对于环论的贡献。

诺特在交换环论方面的成果标志着抽象交换环理论的建立。之后,抽象交换环理论沿着多个方向发展：建立不变量理论与结构理论,如维数及局部环理论；建立表示理论,导致同调代数的发展；更重要的则是逐步几何化,与抽象代数几何融合在一起。特别值得一提的是,受诺特关于交换环的升链条件工作的影响,1927年,阿廷把韦德玻恩(J. H. M. Wedderburn,1882～1948)关于代数的结构定理推广到满足降链条件的非交换环。带有零根的这样的环现在称为阿廷环。他证明阿廷环能分解为单环的直和,而单环是可除环上的矩阵环。1930年,科特(G. Köthe,1905～1989)引进根基的概念,并试图把根基理论推广到更一般的环上,由此开辟了结合环理论的未来方向。一般结合环理论的发展呈多样性,其中重要的有群代数和PI代数。群代数来源于诺特把超复数系与群表示论的结合。PI代数是满足多项式等式的结合代数,与李代数及群论的伯恩赛德问题密切相关。非结合环及非结合代数的主要研究领域有李代数及若尔当代数,另外还有交错代数及幂结合代数。总之,在抽象交换环论建立之后,其自身的研究领域继续不断拓展和深化,同时也促进了整个环论的发展,这可以说是现代数学产生和发展的一个基础。

致 谢 衷心感谢审稿专家提出的宝贵建议和意见!

1 Lam T. Y.AFirstCourseinNoncommutativeRings[M]. New York: Springer-Verlag, 1991.

2 Kleiner I. From Numbers to Rings: The Early History of Ring Theory[J].ElementederMathematik, 1998, 53: 18～35.

3 Van der Waerden B. L.AHistoryofAlgebra:Fromal-KhwarizmitoEmmyNoether[M]. Berlin/New York: Springer, 1985. 3～46.

4 Corry L.ModernAlgebraandtheRiseofMathematicalStructures[M]. Berlin: Birkäuser Verlag, 2004. 92～253.

5 Corry L. The Origins of the Definition of Abstract Rings[J].ModernLogic, 2000, 8: 5～27.

6 Kleiner I.AHistoryofAbstractAlgebra[M]. New York: Springer, 2007. 41～50.

7 Kleiner I. The Genesis of the Abstract Ring Concept[J].TheAmericanMathematicalMonthly, 1996, 103(5): 417～424.

8 Goldstein C., Schappacher N., Schwermer J.TheShapingofArithmeticafterC.F.Gauss’sDisquisitionesArithmeticae[M]. New York: Springer, 2005. 15～47.

9 Gray J. J., Parshall K. H.(ed.)EpisodesintheHistoryofModernAlgebra(1800—1950)[M]. American Mathematical Society/London Mathematical Society, 2007. 1～20.

10 Edwards H. M. Mathematical Ideas,Ideals,and Ideology[J].TheMathematicalIntelligencer, 1992, 14(2): 7.

11 Edwards H. M. Postscript to The Background of Kummer’s Proof of Fermat’s Last Theorem for Regular Primes[J].ArchiveforHistoryofExactSciences, 1977, 14: 219～236.

12 Edwards H. M. The Genesis of Ideal Theory[J].ArchiveforHistoryofExactSciences, 1980, 23(4): 321～378.

13 Edwards H. M. Dedekind’s Invention of Ideals[J].BulletinoftheLondonMathematicalSociety, 1983, 15: 8～17.

14 Edwards H. M. An appreciation of Kronecker[J].TheMathematicalIntelligencer, 1987, 9(1): 28～35.

15 Kimberling C. Emmy Noether[J].AmericanMathematicalMonthly, 1972(79): 136～149.

16 Ne’eman Y. The Impact of Emmy Noether’s Theorems on XX1st Centry Physics[C].TheheritageofEmmyNoether, 1996: 83～101.

17 Brewer J. W., Smith M. K.(ed.)EmmyNoether:ATributetoHerLifeandWork[M]. New York: Marcel Dekker, 1981: 31～43; 65～111; 132～133; 145～156.

18 Kramer E. Noether, Amalie Emmy[C].DictionaryofScientificBiography,vol.X, New York: Charles Scribner’s Sons, 1974: 137～139.

19 Dick A.EmmyNoether: 1882—1935[M]. Boston: Birkhäuser, 1981.

20 Noether M. Paul Gordan[J].MathematischeAnnalen, 1914, 75 (1): 1～41.

21 Fraenkel A. H. über die Teiler der Null und die Zerlegung von Ringen[J].JournalfurdiereineundangewandteMathematik, 1914, 145: 139- 176.

22 Sono M. On Congruences (I-IV)[J].Mem.Coll.Sci.Kyoto, 1917, 2: 203～226; 1918, 3: 113～149, 189～197, 299～308.

23 Noether E., Schmeidler W. Moduln in nichtkommutativen Bereichen, insbesondere aus Differenzial-und Differenzausdrücken[J].MathematischeZeitschrift, 1920, 8: 1～35.

24 Noether E. Idealtheorie in Ringbereichen[J].MathematischeAnnalen, 1921, 83: 24～66.

25 Noether E. Abstrakter Aufbau der Idealtheorie in algebraischen Zahl-und Funktionskörper[J].MathematischeAnnalen, 1927, 96: 26～61.

26 熊全淹. 环论[M]. 武汉: 武汉大学出版社, 1993. 43～45.

27 Lasker E. Zur Theorie der Moduln und Ideale[J].MathematischeAnnalen, 1905, 60: 20～116.

28 Weyl H. Emmy Noether[J].ScriptaMathematica, 1935(3): 201～220.

29 Van der Waerden B. L. The school of Hilbert and Emmy Noether[J].BulletinoftheLondonMathematicalSociety, 1983, 15 (1): 1～7.

Emmy Noether’s Contributions to Commutative Ring Theory

WANG Shuhong, DENG Mingli

(CollegeofMathematicsandInformationScience,HebeiNormalUniversity,Shijiazhuang050024,China)

As an important branch of mathematics, abstract algebra mainly studies the mathematical structures of groups, rings, fields, modules, lattices, etc. Ring theory is one of the deepest areas in abstract algebra. According to whether multiplication is commutative or non-commutative, rings are classified into commutative rings and non-commutative rings. Based upon a large number of original documents and research results, the reason why Emmy Noether turned her research from invariant theory to commutative ring theory is elucidated. An attempt is made to reveal how she constructed the abstract theory of commutative rings through the introduction and skilled application of the ascending chain condition, and thus promoted the subject of abstract algebra.

abstract algebra, Emmy Noether, commutative rings, ascending chain condition

2015- 08- 25；

2016- 07- 08 作者简介：王淑红,1976年生,河北黄骅人,副教授,研究方向为代数学及近现代数学史；邓明立(通讯作者),1962年生,河北辛集人,教授,研究方向为代数学及近现代数学史。 基金项目：国家自然科学基金(项目编号：11271108；11401161)

N091∶O11

A

1000- 0224(2016)04- 0477- 10