孟 伟, 马 丽

(1.云南民族大学 数学与计算机科学学院，云南 昆明 650031;2.曲靖师范学院 数学与信息科学学院，云南 曲靖 655011)

非交换子群共轭类的一个注记

孟 伟1, 马 丽2

(1.云南民族大学 数学与计算机科学学院，云南 昆明 650031;2.曲靖师范学院 数学与信息科学学院，云南 曲靖 655011)

设G是有限群. 用τ(G)表示G中非交换子群的共轭类数,π(G)表示G的素因子的集合.对于每个非交换群有τ(G)≥2|π(G)|-2或|π(G)|+1.分析上述不等式中等号成立的有限群的分类.

交换子群;共轭类;同构分类

0 引言

对于有限群. 通过一些特殊子群的共轭类刻画有限群的属性， 一直是群论研究的热点，同时也是一个难点.文献[1]研究了非正规子群共轭类对有限群结构的影响. 主要考虑非交换子群的共轭类. 用τ(G)表示群G中非交换子群的共轭类数,π(G)表示G的素因子的集合.τ(G)=1等价于G是每个子群皆交换的非交换群, 这类群已被Miler和Moreno[2]完全分类. 2011年，史江涛和张翠[4]证明满足τ(G)≤3的群可解，并且定出τ(G)=4的非可解群只有60阶非交换单群A5.2012年周志浩和郭秀云[5]给出了τ(G)=2有限群的同构分类.笔者在文献[6]中,考虑满足不等式τ(G)≤|π(G)|的有限群，得到这类群是可解的并给出完全分类. 同时得到τ(G)的一个下界, 即证明了如下定理:

定理 设G是一个有限非交换群, 则下列之一成立：

1) 如果G是一个非交换的可解群, 且G的每个Sylow子群交换， 那么τ(G)≥2|π(G)|-2；

2) 如果G是一个非交换的可解群, 且G至少有一个非交换的Sylow子群， 那么τ(G)≥2|π(G)|-1;

3) 如果G是一个非可解群，那么τ(G)≥|π(G)|+1.

1 预备引理

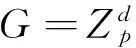
引理1[2]设G是一个群，则τ(G)=1当且仅当G同构与下列群之一,

1) 四元数群Q8;

2)Mn,m,p=[a,b|apn=bpm=1,ab=a1+pn-1];

3)Nn,m,p=[a,b,c|apn=bpm=cp=1,[a,b]=c,[a,c]=[b,c]=1];

4)p-基本群.

引理2[5]设G是一个群且|π(G)|=2. 假若G有一个非交换的Sylow子群，则τ(G)=2当且仅当同构与下列群之一,

1)Q8×Zq;

2)Mn,m,p×Zq;

3)Nn,m,p×Zq;

4)Q8∶Z3;

5)N1,1,p∶Zq, 其中对每个Zq-不变子群H满足[H,Zq]=1.

2 主要结果

定理1 设G是有限可解. 则τ(G)=2|π(G)|-2当且仅当G同构于H×Zm，其中H是p-基本群，(|H|,m)=1且m无平方因子.

证明 充分性是显然的，只证必要性.

设|π(G)|=n≥2. 令π(G)={p1,p2,p3,…,pn}， 由于G是可解群，所以G拥有Sylow系. 设集合 S={P1,P2,P3,…,Pn}是G的Sylow系，其中Pi∈Slypi(G)，i=1,2,…,n，则对集合{1,2,…,n}的任意一个子集{i1,i2,…,ik}，Pi1Pi2…Pik是G的子群[3].

先证G的每个Sylow子群Pi是交换群. 若否，则G至少有一个Sylow子群是非交换群，不失一般性，可假设Sylow子群P1是一个非交换群. 考虑集合Ω={P1Pi1Pi2…Pik|{i1,i2,…,ik}⊆{2,…,n}}， 则|Ω|=2n-1. 由于P1是Ω中的每个群的子群，所以Ω中的每个子群皆为非交换子群并且这些子群的阶是互不相同，因而它们两两互不同构. 从而有τ(G)≥|Ω|=2n-1，这与τ(G)=2|π(G)|-2矛盾. 所以G的每个Sylow子群Pi是交换的.

如果n=2， 那么τ(G)=22-2=1，根据引理1知G是一个p-基本群，结论成立. 接下来假设n≥3. 考虑所有形如PiPj(i≠j)的子群，如果这些群皆为交换群，则G也是交换群. 因此必存在某个子群PiPj(i≠j)是非交换群，不失一般性，可假设H=P1P2是一个非交换子群. 令Ω={HPi1Pi2…Pik|{i1,i2,…,ik}⊆{3,…,n-1}}，则有|Ω|=2n-2. 显然Ω中的每个子群皆包含H，所以Ω中的每个子群皆为非交换子群并且这些子群的阶是互不相同，因而它们两两互不同构. 由于τ(G)=2n-2=|Ω|，所以G的每个非交换子群的共轭类必在Ω中有一个代表. 因此我们得到H是一个极小非交换群，即τ(H)=1.根据引理1知，H是一个p-基本群. 进一步知所有形如PiPj(i≠j,{i,j}≠{1,2})的子群皆为交换群. 所以我们得到G=H×K，其中K=P3P4…Pn是一个交换群. 如果某个Pi的阶大于pi, 取Pi的一个非平凡的真子群L，则HL也是G的一个非交换子群且|HL|不等于Ω中任一子群的阶，这矛盾于τ(G)=2n-2. 所以K是无平方因子阶的交换群，从而K是一个循环群. 定理结论成立.

定理2 设G是有限可解.τ(G)=2|π(G)|-1当且仅当G是下列情形之一：

1)G≅P×Zm, 其中P∈Slyp(G)，τ(P)=1， (p,m)=1，且m无平方因子；

2)G≅(Q8∶Z3)×Zm其中(6,m)=1且m无平方因子；

3)G≅N1,1,p∶Zm，其中对每个Zm-不变子群H满足[H,Zm]=1 且m无平方因子.

证明 充分性是显然的，我们只证必要性.

设|π(G)|=n≥2. 令π(G)={p1,p2,p3,…,pn}， 由于G是可解群，所以G拥有Sylow系. 设集合 S={P1,P2,P3,…,Pn}是G的Sylow系，其中Pi∈Slypi(G)，i=1,2,…,n，则对集合{1,2,…,n}的任意一个子集{i1,i2,…,ik}，Pi1Pi2…Pik是G的子群.

根据定理1的证明可知，G必有一个非交换的Sylow子群. 不失一般性，假设Sylow子群P1是一个非交换群. 重记P=P1，考虑集合Ω={PPi1Pi2…Pik|{i1,i2,…,ik}⊆{2,…,n}}， 则|Ω|=2n-1. 由于P是Ω中的每个群的子群，所以Ω中的每个子群皆为非交换子群并且这些子群的阶是互不相同，因而它们两两互不同构. 从而我们有τ(G)=|Ω|，所以G的每个非交换子群的共轭类必在Ω中有一个代表. 因此有τ(P)=1， 且每个形如Pi1Pi2…Pik({i1,i2,…,ik}⊆{2,…,n})的子群是交换群. 特别地，子群K=P2P3…Pn也是一个交换群. 接下来分2种情况考虑:

1)情形1，G幂零.

此时有G=P×K. 类似定理1的证明可知K是无平方因子的循环群，因此定理结论1)成立.

2)情形2，G非幂零.

此时PPi(i=2,…,n)至少有一个是非幂零群，不失一般性，假设H=PP2是一个非幂零群. 由集合Ω的属性可知τ(H)=2. 根据引理2知：H≅Q8:Z3或N1,1,p:Zq.

假设H≅Q8:Z3，则有G=P×L, 其中L=P3…Pn. 类似类似定理1的证明可知L也是无平方因子的循环群，因此定理结论2)成立.

假设H≅N1,1,p:Zq，类似上面讨论可得定理结论3)成立.

定理3 设G是有限非可解. 则τ(G)=|π(G)|+1当且仅当G≅A5.

证明 见文献[1]的定理1.2.

[1] 孟伟，史江涛.有限群中非正规子群数量的一个标注[J].云南民族大学学报：自然科学版,2010,19(5):360-362.

[2] MILLER G A, MORENO H C. Non-abelian groups in which every subgroup is abelian[J]. Transactions of the American Mathematical Society, 1903, 4(4): 398-404.

[3] ROBINSON D J. A Course in the Theory of Groups [M].Berlin： Springer, 1980：232-234.

[4] SHI J T, ZHANG C. Some sufficient conditions on the number of non-abelian subgroups of a finite group to be solvable[J]. Acta Mathematica Sinica, English Series, 2011, 27(5): 891-896.

[5] 周志浩，郭秀云.非交换子群的共轭类为2的有限群[J] .上海大学学报: 自然科学版，2012，18(1): 35-39.

[6] MENG W.Finite groups with few non-abelian subgroups[J].Comm Algebra,2015,43(3):909-915.

[7] 陈重穆.内外Σ群与极小非Σ群[M]. 重庆：西南师范大学出版社，1988：11-12.

(责任编辑 梁志茂)

A note on conjugacy classes of non-abelian subgroup

MENG Wei1,MA Li2

(1.School of Mathematics and Computer Science，Yunnan Minzu University,Kunming 650031,China;2.College of Mathematics and Information Science, Qujing Normal University,Qujing 655011,China)

LetGbe a finite group andτ(G)denote the number of conjugacy classes of all non-abelian subgroups ofG.The symbolπ(G)denotes the set of the prime divisors ofG.In which paper,Finitegroupswithfewnon-abeliansubgroups, showsτ(G)≥2|π(G)|-2or|π(G)|+1 for every non-abelian groupG,and determines the classification of the finite groups when an equality holds in the above-mentioned inequalities.

abelian subgroup;conjugacy class;automorphism classification

2014-05-26.

国家自然科学基金(11361075).

孟伟(1981-)，男，硕士，副教授.主要研究方向：群及其表示.

O152.1

A

1672-8513(2015)01-0034-03