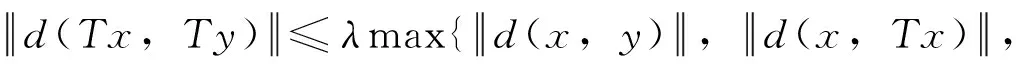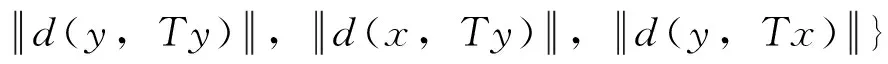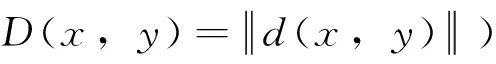具有Banach代数的锥度量空间上拟压缩映射的新不动点定理*
2015-06-08许绍元周作领
许绍元,马 超,周作领
( 1. 韩山师范学院数学与统计学系, 广东 潮州 521041;2. 澳门科技大学资讯科技学院,中国 澳门;3. 中山大学岭南学院, 广东 广州 510275)
具有Banach代数的锥度量空间上拟压缩映射的新不动点定理*
许绍元1,马 超2,周作领3
( 1. 韩山师范学院数学与统计学系, 广东 潮州 521041;2. 澳门科技大学资讯科技学院,中国 澳门;3. 中山大学岭南学院, 广东 广州 510275)
以Banach代数取代Banach空间作为锥度量空间的底空间,引入具有Banach代数的锥度量空间,在正规性条件下已经得到了关于拟压缩映射的不动点定理。删去正规性条件,利用c-序列理论同样得到了拟压缩映射的不动点存在唯一性,主要结果改进和推广了相关文献的一些结论。
具有Banach代数的锥度量空间;非正规锥;不动点定理;拟压缩映射;c-序列
设(X,d)为完备度量空间。映射T:X→X称为一个拟压缩映射(简称拟压缩), 如果存在k∈(0,1),对任意x,y∈X, 总有
d(Tx,Ty)≤kmax{d(x,y),d(x,Tx),
d(y,Ty),d(x,Ty),d(y,Tx)}
Ciric[1]引入此定义并且将它作为更广泛的一类压缩映射进行研究。他证明了一个著名的结果:完备度量空间上任意拟压缩映射必有唯一的不动点。2007年,Huang等[2]引入锥度量空间,推广了通常的度量空间。近年来, 一些作者在锥度量空间中研究拟压缩映射,得到了一些重要结果,见文[3-7]。
最近, 刘浩等[8]引入具有Banach代数的锥度量空间,在正规性的条件下得到了关于拟压缩映射的不动点定理。本文则删去了文[8]中正规性条件,利用c-序列理论同样得到了拟压缩映射的不动点存在唯一性,其主要结果改进了和推广了相关文献的一些结论。
自锥度量空间提出后,一些作者就映射的不动点存在性研究了锥度量空间是否等价于度量空间的问题,见文[9-12]。正如文[13]所言, 我们可以断言具有 Banach 代数A的锥度量空间(X,d)并不等价于度量空间(X,d*), 这里的距离d*定义为d*=ξe∘d, 其中非线性参数函数[9-10]ξe:A→R(e∈intP) 定义为
ξe(y)=inf{r∈R:y∈re-P}
因此,本文进一步研究无正规条件下的锥度量空间中拟压缩映射的不动点定理是有意义的。
1 预备知识
以下总假A为实 Banach 代数, 即A是具有乘法运算的实 Banach 空间, 其运算具有如下性质(对任意x,y,z∈A,α∈R):
(i) (xy)z=x(yz);
(ii)x(y+z)=xy+xz以及(x+y)z=xz+yz; (iii)α(xy)=(αx)y=x(αy);
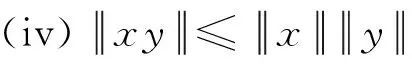
本文总假设实 Banach 代数A具有单位元 (即乘法单位元)e,它满足对任意x∈A均有ex=xe=x。一个元素x∈A称为可逆的,如果存在一个元素(称为它的一个逆元)y∈A使得xy=yx=e。x的逆元记为x-1,详见文[14]。
下面的著名结论在本文中是十分有用的(见文[14])。
命题1 设A是具有单位元e的 Banach代数,x∈A。若x的谱半径ρ(x)小于1, 即
则e-x是可逆的,并且有
下面回顾Banach代数中的锥和半序的概念。Banach代数A中一个子集P称为一个锥,若满足下列条件:
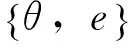
(ii)αP+βP⊂P对任意非负实数α,β均成立;
(iii)P2=PP⊂P;
(iv)P∩{-P}={θ},
其中θ为Banach代数A中的零元。对于锥P⊂A, 定义半序≤如下:x≤y当且仅当y-x∈P;x 锥P称为正规的,如果存在M>0使得对任意x,y∈A, 有 满足上述条件的最小正数M称为P的正规常数[2]。 下文我们假定P为 Banach代数A中的体锥 (即满足intP≠Ø。并且≤是由P确定的半序。 定义 1[2,8,13]设X为非空集。若映射d:X×X→A满足 (i)θ≤d(x,y)对任意x,y∈X成立并且d(x,y)=θ当且仅当x=y=θ; (ii)d(x,y)=d(y,x)对任意x,y∈X成立; (iii)d(x,y)≤d(x,z)+d(z,y)对任意x,y,z∈X成立, 则d称为X上的一个锥距离, (X,d)称为具有Banach代数A的锥距离空间。 定义 2[2,8,13]设(X,d)为具有Banach代数A的锥距离空间,x∈X且{xn}为X中的序列。则 (ii) 称{xn}为Cauchy列, 若对任意满足θ≪c的向量c∈A, 存在正整数N使得d(xn,xm)≪c对任意n,m≥N成立。 (iii) (X,d)称为完备的锥距离空间, 若(X,d)中任意Cauchy列在(X,d)中都收敛。 下面给出两个有用的引理。 引理1[15-16]设E为具有体锥P的Banach空间。若θ≤u≪c对任意θ≪c成立, 则u=θ。 下面给出具有 Banach 代数的锥距离空间中拟压缩映射的定义。 定义 3[8]设(X,d)为具有Banach代数A的锥距离空间。 映射T:X→X称为拟压缩, 如果对于任意满足ρ(k)<1的k∈P以及x,y∈X有 d(Tx,Ty)≤ku (1) 其中 本节将删去文[8]中所要求正规性条件, 利用c-序列理论得到了具有Banach代数的锥距离空间中拟压缩映射的不动点定理。 我们要用到如下的c-序列的有关结论。 定义 4[17-18]设P为Banach代数A中的体锥。序列{un}⊂P称为c-序列, 如果对任意θ≪c, 存在正整数N使得un≪c对任意n≥N成立。 利用c-序列的定义不难得到如下简单的结论。 命题 2[17,19]设P为Banach代数A中的体锥,{un}和{vn}均为P中的序列。 若{un}和{vn}都是c-序列且α,β>0, 则{αun+βvn}也是c-序列。 除了上述命题2外, 下列几个命题在本文主要结果的证明中是至关重要的。 命题 3[19]设P为Banach代数A中的体锥, {un}为P中的序列。若k∈P是任意给定的向量且{un}是c-序列, 则{kun}也是c-序列。 命题 4[19]设(X,d)为具有Banach代数A的锥距离空间且P为A中的体锥。 设{xn}为X中的序列。若{xn}收敛于x∈X, 则 (i) {d(xn,x)}是c-序列。 (ii) 对任意p∈N, {d(xn,xn+p)}也是c-序列。 下面给出本文的主要的结果。 定理1 设(X,d)为具有Banach代数A的完备的锥距离空间,k∈P。若映射T:X→X为拟压缩, 满足条件(i), 则T在X中有唯一的不动点。并且对任意的x∈X, 迭代序列{Tnx}收敛于该不动点。 证明 任意选取x0∈X, 记xn=Tnx0。首先证明 d(xi,xj)≤k(e-k)-1d(x0,x1),∀i,j≥1 (2) (2)式的证明与文[8, 引理10]中的(7)式一致, 这是因为文[8, 引理10]中的(7)式的证明不需要使用正规性条件。 下证{xn}是 Cauchy 列。 对任意 1 由拟压缩的定义, 对任意u∈C(m,n), 存在v∈C(m-1,n), 使得u≤kv。于是, 这里 其中最后的不等式由(2)式得到。 由引理2以及 d(xn,xm)≤km(e-k)-1d(x0,x1)≪c 故{xn}是Cauchy列。 其次证明不动点的存在性。 由(X,d)的完备性, 存在x*∈X使得xn→x*。于是, 其中 若u=d(xn-1,x*),d(xn-1,xn)或u=d(x*,xn), 则分别有 若u=d(x*,Tx*), 则 于是 若u=d(xn-1,Tx*), 则 考虑到(e-k)-1≥θ,于是有 因此, 无论哪种情形, 由定义4和命题2-4,有d(x*,Tx*)≤yn, 其中{yn}是锥P中c-序列。于是, 对任意θ≪c,有θ≤d(x*,Tx*)≪c。因此, 由引理1有d(x*,Tx*)=θ, 故x*为T的不动点。 最后证明不动点的唯一性。证明方法同文[8, 定理 9 ]。 注2 与文 [8, 定理9]相比, 本文定理1不需要锥P的正规性条件, 因此定理1改进和推广了文[8, 定理9]。 d(Tx,Ty)≤ku 有 于是有 注4 在定理1中令A=R,P=[0,+∞), 则利用通常的范数我们可以得到文[1]的主要结果, 即完备度量空间中的Ciric 压缩映射不动点定理。这表明定理1推广了文[1,15]的主要结论。 [1] CIRIC L J B. A generalization of Banach’s contraction principle [J]. Proc Amer Math Soc, 1974, 45: 267-273. [2] HUANG L G, ZHANG X. Cone metric spaces and fixed point theorems of contractive mappings [J]. J Math Anal Appl, 2007, 332: 1468-1476. [3] AL-KHALEEL M, AL-SHARIFA S, KHANDAQJI M. Fixed points for contraction mappings in generalized cone metric spaces [J]. Jordan J Math Stat, 2012, 5(4): 291-307. [4] GAJIC L J, RAKOCEVIC V. Quasi-contractions on a nonnormal cone metric space [J]. Funct Anal Appl, 2012, 46(1): 75-79. [5] ILIC D, RAKOCEVIC V. Quasi-contraction on a cone metric space [J]. Appl Math Lett, 2009, 22(5): 728-731. [6] KADELBURG Z, REDENOVIC S, RAKOCEVIC V. Remarks on “Quasi-contraction on a cone metric space” [J]. Appl Math Lett, 2009, 22(11): 1674-1679. [7] KADELBURG Z, PAVLOVIC M, REDENOVIC S. Common Fixed point theorems for ordered contractions and quasi-contractions in ordered cone metric spaces [J]. Comput Math Appl, 2010, 59: 3148-3159. [8] LIU H, XU S. Fixed point theorem of quasi-contractions on cone metric spaces with Banach algebras [J]. Abstract and Applied Analysis, 2013, Article ID 187348. [9] CAKALL H, SONMEZ A, GENC C. On an equivalence of topological vector space valued cone metric spaces and metric spaces [J]. Appl Math Lett, 2012, 25: 429-433. [10] DU W S. A note on cone metric fixed point theory and its equivalence [J]. Nonlinear Analysis, 2010, 72(5): 2259-2261. [11] KADELBURG Z, REDENOVIC S, RAKOCEVIC V. A note on the equivalence of some metric and cone metric fixed point results [J]. Appl Math Lett, 2011, 24: 370-374. [12] FENG Y, MAO W. The equivalence of cone metric spaces and metric spaces [J]. Fixed Point Theory, 2010, 11(2): 259-264. [13] LIU H, XU S. Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings [J]. Fixed Point Theory and Applications, 2013, 2013: 320. [14] RUDIN W. Functional analysis [M]. 2nd ed. 北京:机械工业出版社, 2006. [15] JANKOVIC S, KADELBURG Z, REDENOVIC S. On the cone metric space: A survey [J]. Nonl Anal, 2011, 74: 2591-2601. [16] REDENOVIC S, RHOADES B E. Fixed point theorem for two non-self mappings in cone metric spaces [J]. Comput Math Appl, 2009, 57: 1701-1707. [17] KADELBURG Z, REDENOVIC S. A note on various types of cones and fixed point results in cone metric spaces [J]. Asian Journal of Mathematics and Applications, 2013, Article ID: ama 0104. [18] DORDEVIC M, DORIC D, KADELBURG Z, et al. Fixed point results under c-distance in tvs-cone metric spaces [J]. Fixed Point Theory Appl, 2011, 2011: 29. [19] XU S, REDENOVIC S. Fixed point theorems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality [J]. Fixed Point Theory and Applications, 2014, 2014: 102. A New Fixed Point Theorem of Quasi-Contractions on Cone Metric Space XUShaoyuan1,MAChao2,ZHOUZuoling3 (1. School of Mathematics and Statistics, Hanshan Normal College, Chaozhou 521041, China;2. Faculty of Information Technology, Macao University of Science and Technology, Macao, China;3. School of Lingnan, Sun Yat-sen University, Guangzhou 510275, China) By replacing Banach spaces by Banach algebras as the underlying spaces of cone metric spaces, the concept of cone metric spaces with Banach algebras has been introduced. And a fixed point theorem of quasi-contractions with the assumption of normality has been proved. By omitting the assumption of normality and utilizing the theory ofc-sequence, the existence and uniqueness of the fixed point for the quasi-contractions is obtained in the setting of cone metric spaces with Banach algebras. As a consequence, the corresponding result in the literature is improved and generalized. cone metric spaces with Banach algebras; non-normal cones; fixed point theorems; quasi-contractions;c-sequence 10.13471/j.cnki.acta.snus.2015.05.001 2015-01-16 国家自然科学基金资助项目(11371379);澳门科学技术发展基金资助项目(069/2011/A) ;韩山师范学院2013年创新强系资助项目 许绍元(1964年生),男;研究方向:非线性分析与分形几何; 通讯作者:马超;E-mail:cma@must.edu.mo O177.91 A 0529-6579(2015)05-0001-04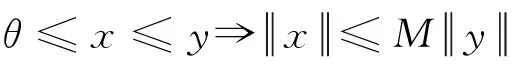




2 主要结果