李时敏

(广东财经大学数学与统计学院，广东 广州 510320)



一类不连续广义Lienard微分系统的极限环分支*

李时敏

(广东财经大学数学与统计学院，广东 广州 510320)

利用不连续微分系统的一阶平均法，研究从一类广义Lienard微分系统中心的周期环域分支出极限环的最大个数问题。通过对该系统的中心进行分段连续的多项式扰动，得到了该系统从中心的周期环域分支出极限环最大个数的线性估计。结果表明：不连续Lienard微分系统比其对应的连续微分系统可以分支出更多的极限环。

极限环；Lienard微分系统；不连续微分系统； 平均法

微分系统定性理论的一个主要问题是研究平面微分系统的极限环问题[1]。例如，众所周知的希尔伯特第16问题就是考虑平面多项式微分系统的极限环个数问题[2]。由于该问题十分困难， Smale[3]仅考虑平面Lienard微分系统，并将其列为21世纪需要解决的重要问题之一。Lienard微分系统在科学以及工程的许多分支都有着广泛的应用[4]。

近年来，随着现实生活中出现许多不连续现象，越来越多的数学工作者开始研究不连续微分系统的分支问题[4]。鉴于不连续微分系统的重要性，本文讨论如下不连续广义Lienard微分系统：

(1)

其中

(2)

记H(l,n,m)为利用一阶平均法， 不连续广义Lienard微分系统(1)从原点的周期环域分支出极限环的最大个数。目前已有许多文献对某些特殊情形进行了讨论，列举如下：

(i) 若fn(x)≡0，文[5]证明了

H(0,0,m)=[(m-1)/2],H(1,0,m)=[m/2],H(2,0,m)=[(m-1)/2]

并且猜测H(l,0,m)=[(m+1-l)/2],l=3,4,5,…。其中[]表示取整函数。

(ii) 若l=0，文[6]得到H(0,n,0)≥[n/2]。文[7]得到H(0,n,m)=[n/2]。

(iii) 若l=1,m=1，文[8]中得到H(1,n,1)≥[n/2]+1。

利用不连续微分系统的一阶平均法定理[9]，本文考虑了系统(1)从原点的周期环域分支出极限环的最大个数问题。我们的主要结果如下：

定理1 当|ε|>0充分小，考虑系统(1) ，

(i) 若l为奇数，则H(l,n,m)≤max{2[n/2]+1,2[m/2]}。特别地,

(ii) 若l为偶数，则H(l,n,m)≤max{[n/2],[(m-1)/2]}。特别地,

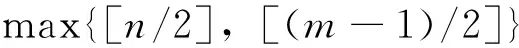
注1 文献[7]中已经证明了H(0,n,n)=[n/2]。由定理1的结论(i)，我们可以得到H(1,n,n)=2[n/2]+1。结果表明 不连续Lienard微分系统(1) (l=1)比其相应的连续系统(l=0)可以从原点的周期环域多分支出[n/2]+1个极限环。当然，我们的结论是建立在现有的结果之上。

1 不连续微分系统的一阶平均法

在这部分里，我们将介绍文[9]中的不连续微分系统的一阶平均法定理。值得注意的是，原文中考虑的是不连续微分方程组。由于本文只涉及单个微分方程，简单起见，我们仅介绍单个微分方程的一阶平均法。粗略地说：平均法给出了非自治微分系统与其相应的平均系统(自治微分系统)解之间的定性关系。有关平均法的一般介绍，可以参考文[10]。

考虑如下不连续微分方程

(3)

其中

(4)

且F1,F2:R×D→R,G1,G2:R×D×(-ε0,ε0)→R,h:R×D→R均为连续函数。D⊂R为开区间。这些函数均关于变量θ为2π的周期函数。sign(u)为符号函数，定义如下：

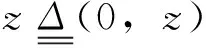
定理2 考虑微分方程(3)，定义平均函数f:D→R如下

(5)

假设满足以下三个条件：

(i)F1,F2,R1,R2和h均关于r满足局部李普希兹条件。

(iii) 若∂h/∂θ≠0，则对所有的(θ,r)∈M，有∂h/∂θ≠0；若∂h/∂θ≡0，则对所有的

(θ,z)∈[0,2π]×Μ有〈▽rh,F1〉2-〈▽rh,F2〉2>0，其中▽rh表示函数h关于变量r的梯度。则当|ε|>0充分小，系统(3)存在一个周期为2π的解r(θ,ε)，使得当ε→0时，r(0,ε)→a(在Hausdorff度量意义下)。

为了方便验证定理2的假设(ii)，我们给出下面的注记。

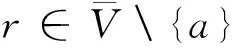
由定理2和注2 可知，若微分系统(3) 满足定理2 中的假设(i)和(iii)，则由式(5)定义的平均函数f(r)的简单零点个数对应微分系统(3)的极限环个数。下面我们开始推导平均函数(5)的具体表达式。

2 平均函数

(6)

其中

(7)

将式(7)代入式(5)，得到平均函数

(8)

其中

(9)

由于

(10)

(11)

根据定理2，需要计算平均函数(11)简单零点的个数。我们分以下两种情况来讨论：

2.1l为奇数

命题1 若l为奇数，则平均函数(11)为

(12)

其中

(13)

因此

类似地，当θ∈(kπ/l,(k+1)π/l)时，

(14)

将式(14)代入式(9)中第二式，有

(15)

显然B2j+1=0。由式(15)可得

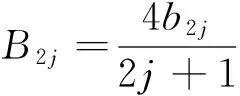
2.2l为偶数

命题2 若l为偶数，则平均函数(11)为

(16)

其中

(17)

因此

(18)

将式(18)代入式(9)中第二式，有

(19)

显然B2j=0。由式(19)可得

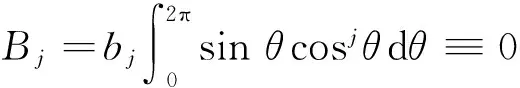
3 定理1的证明

在估计平均函数零点个数的过程中， 我们需要用到如下引理：

定理1的证明 首先考虑情形(i)。

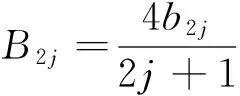
情形(ii)同理可证。

[1] 张芷芬，丁同仁，黄文灶，等. 微分方程定性理论[M]. 北京：科学出版社，1985.

[2] LI J. Hilbert’s 16th problem and bifurcations of planar polynomial vector fields [J]. Int J Bifurcation and Chaos, 2003, 13: 47-106.

[3] SMALE S. Mathematical problems for the next century [J]. The Mathematical Intelligence, 1998, 20: 7-15.

[4] BERNARDO M, BUDD C, CHAMPNEYS A, et al. Bifurcations in nonsmooth dynamic systems [J]. SIAM Review, 2008, 50: 629-701.

[5] LLIBRE J, TEIXEIRA M. Limit cycles form-piecewise discontinuous polynomial Lienard differential equations [J]. Z Angew Math Phys, 2015, 66(1): 51-66.

[6] BLOWS T, LLOYD N. The number of small-amplitude limit cycles of Lienard equations [J]. Math Proc Camb Phil Soc, 1984, 95: 359-366.

[7] LLIBRE J, MEREU A, TEIXEIRA M. Limit cycles for the generalized polynomial Lienard differential equations [J]. Math Proc Camb Phil Soc, 2010, 148: 363-383.

[8] MIRANDA M, MEREU A. Limit cycles in discontinuous classical Lienard equations [J]. Nonlinear Analysis: Real World Applications, 2014, 20: 67-73.

[9] LLIBRE J, NOVAES D, TEIXEIRA M. On the birth of limit cycles for non-smooth dynamical systems [J]. Bull Sci Math, 2015, 139: 229-244.

[10] SANDERS J, VERHULST F. Averaging methods in nonlinear dynamic systems [M]. New York: Springer-Verlag, 1985.

[11] BUICA A, LLIBRE J. Averaging methods for finding periodic orbits via Brouwer degree [J]. Bull Sci Math, 2004, 128: 7-22.

[12] COLL B, GASULL A, PROHENS R. Bifurcation of limit cycles from two families of centers [J]. Dyn Contin Diccrete Impulse Syst, Ser A, Math Anal, 2005, 12: 275-287.

Bifurcation of Limit Cycles for a Class of Discontinuous Generalized Lienard Differential System

LIShimin

(School of Mathematics and Statistics, Guangdong University of Finance and Economics, Guangzhou 510320, China)

Using the first order averaging method for discontinuous differential system, the maximum number of limit cycles which bifurcate from the periodic annulus of the center for a class of generalized Lienard differential system is studied. By piecewise smooth polynomial perturbating, the linear estimation of the maximum number of limit cycles which bifurcate from the periodic annulus of this center is obtained. The result shows that there are more limit cycles which can bifurcate from the discontinuous Lienard differential system than the continuous one.

limit cycle; Lienard differential system; discontinuous differential system; averaging method

10.13471/j.cnki.acta.snus.2015.05.004

2015-03-21

国家自然科学基金青年科学基金资助项目(11401111)

李时敏(1983年生)，男；研究方向：常微分方程及其应用；E-mail:lism1983@126.com

0175

A

0529-6579(2015)05-0015-05