☉江苏省清浦中学 吴洪生

横看成岭侧成峰，远近高低各不同
——也谈“几何法”判断直线与椭圆的位置关系

☉江苏省清浦中学 吴洪生

关于判断直线与椭圆位置的研究，大多数老师是引导学生用代数方法，联立方程组，消元后转化为关于x（或y）的一元二次方程，利用判别式Δ加以研究，由于运算量很大，不少学生做不到底，以至于半途而废.甚至有老师认为，判断直线与椭圆的位置关系，“几何法”行不通，因为椭圆没有统一的半径.此说法有点欠妥.何苗，张全合两位老师在《对直线与有心圆锥曲线位置关系判断的探究》（《数学教学》2012年第9期）一文中用“几何法”为我们做了很好的尝试.事实上，椭圆虽然没有统一的半径，但椭圆上的点到两个焦点的距离之和为定值2a，即对椭圆上任一点，左、右焦半径之和是统一的.因此，我们不妨变换视角，从焦半径入手来探究直线与椭圆的位置关系.

一、引论

（1）点P（x0，y0）在椭圆|PF2|＜2a；

（2）点P（x0，y0）在椭圆|PF2|=2a；

（3）点P（x0，y0）在椭圆|PF2|＞2a.

证明：如图1，当点P在椭圆内时，延长F1P交椭圆于点M，连接MF2，则|PF1|+|PF2|＜|PF1|+|MP|+|MF2|=|MF1|+|MF2| =2a.

图1

图2

如图2，当点P在椭圆上时，|PF1|+|PF2|=2a.（定义）

如图3，当点P在椭圆外时，设PF1交椭圆于点M，则|PF1|+|PF2|=|MF1|+（|PM|+|PF2|）＞|MF1|+|MF2|=2a.

反证可得：当|PF1|+|PF2|＜2a时，点P（x0，y0）在椭圆

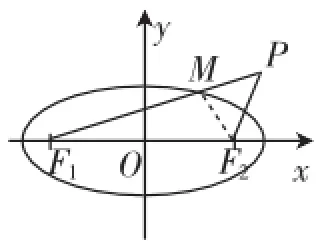
图3

当|PF1|+|PF2|=2a时，点P（x0，y0）在椭圆b＞0）上.

当|PF1|+|PF2|＞2a时，点P（x0，y0）在椭圆b＞0）外.

二、探究

（1）显然，当焦点F1、F2在直线l两侧或直线l过焦点F1（或F2）时，直线l与椭圆相交.

（2）当F1、F2在直线l同侧时.

①如图4，若直线l与椭圆相离，则对l上任一点P恒有|PF1|+|PF2|＞2a，从而有（|PF1|+|PF2|）min＞2a；反之，若（|PF1|+ |PF2|）min＞2a，则l上所有点均在椭圆外，l与椭圆相离.

图4

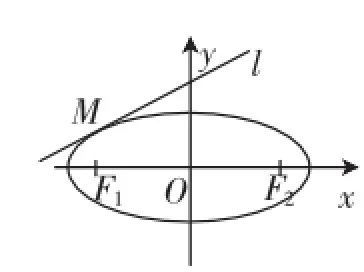
图5

图6

至于，如何求|PF1|+|PF2|的最小值，由于F1、F2在l的同侧，如图7，作F1关于l的对称点F1′，连接F1′F2，则（|PF1|+ |PF2|）min=|F1′F2|.

图7

三、结论

两个焦点F1、F2在直线l同侧时，有：

四、应用

例2（重庆高考题）已知以F1（-2，0）、F2（2，0）为焦点的椭圆与直线有且仅有一个公共点，则椭圆的长轴长为（）.

解：F1（-2，0）关于l的对称点

数学教学是数学思维活动的教学，换个角度思考问题是解决数学问题的重要方法，通过转换角度思考，启迪学生思维，往往能化难为易，化繁为简，广开思路，将复杂问题简单化.在数学课堂活动中，教师要注重培养学生的创新思维能力，让学生学会从多角度思考问题，提高课堂教学的有效性.F