多元视角下的基本不等式再认识<br/>——一道高考题的源与流带来的启示

多元视角下的基本不等式再认识
——一道高考题的源与流带来的启示

2015-04-28浙江省桐乡市凤鸣高级中学沈金兴

中学数学杂志 2015年7期

☉浙江省桐乡市凤鸣高级中学沈金兴

多元视角下的基本不等式再认识
——一道高考题的源与流带来的启示

☉浙江省桐乡市凤鸣高级中学沈金兴

每年6月份的高考如期而至，而综观各个省的高考题，都会有一些新颖的题目.但与此同时，也有一些直接来自于教材上的题目，只不过进行了修改与提炼.所以高考命题者们经常提到一句话，说高考题“源于教材而高于教材”，由此来说明教材的重要性.其实，教材是教学之本，其重要性是不言而喻的，那么能否通过研究高考题来进一步加深对教材中的公式、定理与例、习题等内容的认识呢？答案是肯定的［1］.本文就是根据2014年浙江省的一道高考题，通过挖掘其来源，从而从多角度来认识所要考的某一知识点.

一、高考题呈现

浙江省2014年的理科第17题与文科第10题是同一道题，题目是：如图1，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确命中目标点P，需计算由点A观察点P的仰角θ的大小（仰角θ为直线AP与平面ABC所成的角）.若AB=15cm，AC=25cm，∠BCM= 30°，则tanθ的最大值是_________.其中在文科高考卷中改成了选择题.

对此题的解法，本文不再赘述了，考到的知识点较多，综合性很强，是一道好题.

图1

二、源自教材

该高考题作为理科填空题与文科选择题的压轴题，自有它的道理，因为此题要考查学生的知识与能力众多.首先它具有应用题的性质，要让学生理解题意后分析，然后从立体几何入手，由线面夹角概念继而转化为函数，最后求最值时又要用到基本不等式.可以说从立体到平面，从几何到代数，再到最值问题都涵盖了.但从实际生活常识来看，该题涉及的其实就是最大视角问题，而这种问题曾在人教版教材（必修5）3.4节“基本不是这样的.

图2

如图2，树顶A离地面am，树上另一点B离地面bm，在离地面cm的C处看此树，离此树多远时看A、B的视角最大？

显然，教材上的习题也是日常生活中涉及的视角最大问题，只不过已抽象成在二维平面上讨论，而高考题把它改成了三维空间，在立体空间上讨论射击的视角最大问题，可两者在本质上讨论的是相同问题，所以这道高考题源于教材中的习题.但如果继续挖掘，发现教材上的这道习题又起源于数学史上第一个极值问题［2］.

三、始于Regiomontanus问题

在15世纪的欧洲，有一位德国数学家，叫雷吉奥蒙塔努斯（Regiomontanus，1436-1476），他的著作《论各种三角形》曾对三角学的发展产生了很大影响，是现代三角学的雏形.他于1471年在给朋友的信中就提到了这样一个问题：“一根垂直悬挂的杆子，从地面上哪点看上去它最长（也就是视角最大）？”，这个问题被称为迄今为止数学史上的第一个极值问题，即最大视角问题.

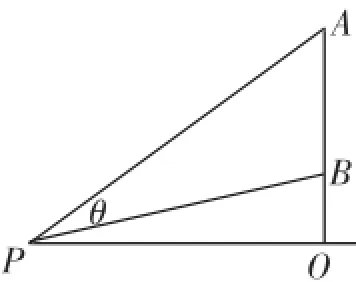
图3

如图3，把杆子表示成线段AB，假设点P是地面上使得θ=∠APB最大的点，则设OA=a，OB=b，OP=x，∠OPA=α，∠OPB= β.所以有：tanθ=tan（α-β）=最大值，即θ取最大值.

由此可见，教材中的习题其实就是雷吉奥蒙塔努斯提出的最大视角问题，两者如出一辙.如果继续深入挖掘，就会发现当θ最大时的其实就是两个正数a、b的几何平均数.观察图3，当OP为OA与OB的几何平均数时，θ最大.此时，如果过P、A、B三点作圆，就会发现该圆与直线OP相切，P为切点，于是对基本不等式≤（*）的几何解释或证明又有了新的认识.

四、基本不等式的再认识：多元视角

图4

1.从历史视角认识：Regiomontanus问题的拓展

受雷吉奥蒙塔努斯问题解决的启发，并对它进一步拓展，于是基本不等式的证明就有了新的方法.

如图4，圆O外一点A，过A作圆O的切线AD，切点为D，连接AO交圆O于C、B.设AC=a，AB=b.由圆O的切割线定理有：AD2=AC·AB=ab，故AD=

2.从几何视角认识：创建几何模型

（1）半圆模型.

图5

上面的证明方法是通过比较线段长短而得，事实上在人教版教材中也提到了这种方法.教材在得出基本不等式后，给出了图5，然后让学生探究基本不等式的几何解释.在图5中，CD⊥AB，AD⊥BD.设BC=a，AC=b，由射影定理可知CD2=AC·BC=ab，即b）.显然，在直角△COD中，CD＜OD，得证，其中图5称为基本不等式的半圆模型.

（2）等腰直角三角形模型.

图6

图7

图6 称为等腰直角三角形模型，是通过比较面积大小证出基本不等式的，而这种方法是直接借鉴了中国古代证明勾股定理的方法：出入相补原理，即面积变换法［3］.事实上，人教版教材在引入不等式a2+b2≥2ab时就是用比较面积大小的方法，模型是赵爽弦图，如图7.所以从几何角度来认识基本不等式，半圆与等腰直角三角形这两个几何模型反映了基本不等式的本质：线段长短或面积大小的直观体现.

3.从代数视角认识：构造数列与方程

（1）构造等差数列.

（2）构造方程.

对两正数a、b，构造一元二次方程（x-a）（x-b）=0，即x2-（a+b）x+ab=0有两个实根a、b，故判别式Δ=（a+b）2-4ab≥0，所以当且仅当a=b时取等号，（*）式得证.

通过构造二次方程，然后利用判别式来推导，方法简单明了，易于理解.所以从纯粹的代数运算来证明基本不等式，也是方法众多，而且很简便，如教材上用的作差法.但不同的方法，可以从各个角度全方位地认识该不等式.

4.从物理学视角认识：运动模型

设想有两个质点A和B做直线运动，其中A做匀速运动，B做加速运动，但质点B还具有这样的性质：随着时间的变化，位移按等比数列变化，换言之，质点B每经过一个相等的时间间隔，位移都增加到前一个位移相同的倍数，这样质点B的运动规律就可表示成：s0、q为常数，q＞1）.如图8，设在时刻t1，质点A与B的位移大小都是a，而在时刻t（2t2＞t1），质点A和B的位移大小都是b（a＜b）.下面来计算质点A与B分别在中间时刻时的位移大小.

图8

由于质点A做匀速运动，所以A在中间时刻正好运动到a、b的中点，即位移为.质点B在a处的位移是：a=在b处的位移是：所以质点B在中间时刻t=

这时候的大小关系是很直观的.因为质点A与B都是从t1时刻的位移a到t2时刻的位移b，两者在相同时间内运动了相同的位移.而质点B做加速运动，所以它在前半段时间的平均速度小于后半段的平均速度，故前半段时间走过的距离必小于后半段所走过的距离，即在时间中点，质点B没有到达位移中点，于是有a=b时等式就成立了.

从物理学角度来认识均值不等式，图8其实就是日常生活中的运动模型，基于生活经验都能很好地理解这个模型，可以说既直观又有生活气息.