☉福建省厦门第一中学 王淼生

从一道哈佛试题浅谈因数构形*

☉福建省厦门第一中学 王淼生

一、著名学府入学试题

世界上最著名的哈佛大学曾有这样一道入学试题，原题如下：

请在下列一组图形符号中找出它们所蕴含的内在规律，然后在图形空白处填上恰当的图形.

剖析：先观察上述所给六个图形，第一个与第四个图形好像都是大写英文字母“M”，只是横线的位置不同而已；第二个图形酷似“心”形；第三个图形似乎“8”字形；第五个图形恰为横杆下面挂一个钢圈；最后一个即第七个图形是倒置的等腰三角形.仅仅从单个图形看很难有所突破，必须将这些图形综合在一起全面考虑，因此需要进一步深入研究图形.

所谓寻找规律，就是寻求共同属性，也就是从上述六个具体的图形中抽象出本质的特征.抽象就是从众多事物中提取共同、本质特征，舍弃个别、非本质特征.要抽象就必须进行比较，没有比较就无法找到本质上共同的部分.共同特征是指那些能把一类事物与他类事物区分开来的特征，这些具有区分作用的特征即为本质属性，因此抽取事物的共同特征就是提炼事物的本质属性，舍弃非本质的特征，就是去粗取精、去伪存真、由表及里的过程.

尽管上述六个图形各不相同，似乎毫无关联，但是有一个共同特征：都是轴对称图形！既然都是轴对称图形，从数学视角只要关注每一个图形右边的一半，因此我们用不透明的纸板把上述每个图形对称轴左边的图形遮住，此时再来观察这些图形，就容易发现这些图形蕴含的规律是阿拉伯数字1、2、3、4、5、7，中间缺少一个数字6，因此只要在第六个位置的横线上方的空白处画出图形是数字“6”的特征图形，然后运用轴对称的性质画出左边对应的图形并组合于一体即可（详见文1）.

傲视全球的哈佛大学居然把看似如此简单的问题作为入学考题，简直让人不可思议！从一个侧面反映了美国等发达国家的数学教育何等重视数形结合思想的渗透与考查.遗憾的是我国数学教育在数学思想方面显得较为薄弱，时至今日，尽管我国新一轮课改实施十余年，尽管新课标教材明显提高了对数学思想方法的要求，但是不少教师依然抱着“冷战思维：题海战术”，依然还是老一套：一个概念、三个注意，外加无休止的所谓强化训练，依然还是带着极端功利的思想：重数量、重知识、重方法、重结果而轻质量、轻能力、轻过程、轻思想.

二、数形结合思想

恩格斯指出：“数学是研究现实世界的量的关系与空间形式的科学.”数学的研究对象是数量关系和空间形式，“数”与“形”有着十分密切的联系，可以说宇宙间万物几乎都融入“数”与“形”的矛盾统一体之中.正因为如此，数形结合思想几乎无处不在、无时不在.

正是基于对数与形的深入研究才产生数学这门学科，从而让人们从不同的侧面来认识事物，进而把对数量关系的研究转化为对图形性质的研究，或者把对图形性质的研究转化为对数量关系的研究.这种解决问题过程中的“数”与“形”不断地相互转化的研究策略，就是数形结合思想的具体体现.数形结合思想是一种极其重要的数学思想，数形结合使得抽象的数学语言与直观的几何图形有机结合起来，使得抽象思维与形象思维融为一体.

数形结合就是根据数学问题的条件和结论之间的内在联系，既要分析其代数意义，又要揭示其几何直观背景，充分利用数与形的关系，寻找解题思路，使问题化难为易、化繁为简，从而达到解决问题的目的.数形结合既是一种重要的数学思想又是一种重要的数学方法，包含“以形助数”和“以数构形”两个方面.借助形的直观性来阐明数量之间的关系，即以形为手段，以数为目的；或者借助于数的精确性和严密性来阐明形的某些属性，即以数为手段，以形为目的.运用数形结合，由“形”到“数”转化往往明显，而由“数”构“形”则需要强烈的转换意识及敏锐的构造能力，因此，数形结合思想关键在于侧重从“数”到“形”的转化，通俗地说就是依据数的特征来构造几何图形.

值得注意的是：绝大多数人认为这个“数”就是狭义的数，其实这个数是一个广义的数，即可以是纯粹的数字，还可以是式子（包括方程、不等式等），甚至可以是数学问题（包括生活问题），本文拟从几个实例来阐述由数如何构造最简单、最熟悉的平面几何图形（线、三角形等）、立体几何图形（三棱锥、长方体等）、平面解析几何图形（圆、椭圆等）及空间解析几何图形（平面、球等）.

三、由数构形的策略

1.由数（数字、代数式）构造平面几何图形模型

平面几何中最简单的图形就是直线（包括射线、线段）、三角形.有些数学问题看似是纯代数问题，若从代数方面入手则十分复杂，如果注意观察数量关系、观察外形结构、观察所求结论，然后对已知条件及所求结论深入剖析会发现：这些表面上的代数问题其实与几何图形密不可分，于是构造几何图形，往往会得到意想不到的收获.

剖析：上述求和代数式中的分式分别表示1的一半、一半的一半、…，这不正是“一尺之棰，日取其半，万世不竭”的再现吗？据此构造AB=1的一条线段（即一尺之棰），取AB的中点A1，再取线段A1B的中点A2，再取线段A2B的中点A3（日取其半），如此不断反复取下去（万世不所有这些线段长度之和为1，即：

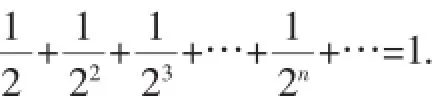
评注：案例1是2008年广东省高考试题，所求和的代数式表明是一个无穷级数求和，而且是无穷等比递减数列，因此利用极限思想构造线段，让人赏心悦目，这正是数形结合的魅力所在！当然，本题还可以构造面积为1的正方形，然后将这个正方形不断反复对折下去即可.

2.因数（不等式、实际问题）构造立体几何图形模型

立体几何中最简单的几何图形就是长方体及三棱锥等，妥善构造这些几何体，并利用这些几何体本身具有的代数性质（尤其是长方体的几何与代数性质！），达到四两拨千斤的奇效.

案例2：世界上任何6个人中，总可以找到3个相互认识的人或者3个互相不认识的人.

剖析：我们把6个人看作6个顶点，互相认识的2个人对应的顶点连成红线，否则连成蓝线，那么本问题就等价于在6个顶点中的每2个点之间用红线或者蓝线相连，则至少存在一个同色三角形.

我们任取一个顶点为A，则A与其余5个顶点的连线共有5条线，由于只有红与蓝两色，依据抽屉原理可得至少存在3条线是同色，不妨设AB、AC、AD同是红色，此时构造三棱锥A－BCD，下面我们来考察△BCD，若BC、CD、DB三线中至少有一条红色线，不妨设BC，则含有一个红色三角形，即△ABC是红色三角形，即存在一个同色三角形，否则△BCD就是蓝色三角形，至此本问题得以解决.也就是说：世界上任何6个人中，必有3个人或者相互认识或者互不认识！多么不可思议的命题，却是千真万确的真理！

案例3：若α、β、γ均为锐角，且sin2α+sin2β+sin2γ=1，证明：

剖析：注意到已知条件：三锐角正弦的平方和等于1，这不正是长方体一个重要的代数性质吗？即长方体的体对角线与共点的三个面所成的角α、β、γ的正弦的平方和等于1，因此构造长、宽、高分别为a、b、c的长方体，将复杂的三角问题顺利转化为不等式问题，因此所求证的原不等式等价于：

利用基本不等式：a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca，则只要证明：

不妨令abc=1，则上式等价于：

上式正是调和平均数与算术平均数之间的关系.

评注：匈牙利数学家罗莎指出：“解决数学问题时往往不是对问题实行正面攻击，而是不断地将它构造、变形，直至把它转化成能够得到解决的问题.”上述由数构形，再由形辅数的策略，正是罗莎名言的最佳诠释与践行.

案例2是1947年匈牙利数学奥林匹克竞赛试题，它仅仅是著名的拉姆赛定理的一个特例.拉姆赛定理：设空间6个点中任意4点不共面，若将其中两点间的连线染成红色或者蓝色之一，则必然存在一个三边颜色相同的三角形.

案例3为2005年咸阳市教师技能大赛压轴题，因求证结论极其复杂，原解答直接从三角化简、变形入手，显得特别复杂、冗长，通过构造长方体可获得妙不可言的解答.

3.因数（代数式）构造平面解析几何图形模型

解析几何本身就是数形结合的产物，这正是解析几何的精髓所在.解析几何中最简单的几何图形就是圆、椭圆、双曲线及抛物线等，由圆锥曲线（包括圆）的定义可知圆锥曲线具有鲜明的特征，抓住其本质特征，往往可找到构造圆锥曲线的入口，并妥善利用圆锥曲线的定义、性质迅速解决问题.

案例4：已知α、β为锐角，且sin（α+β）=2sinα.证明β＞α.

剖析：构造直径AB=1的圆，在AB的上方、下方的圆弧上分别取点C、D，使∠CAB=α，∠DAB=β，则BC=sinα，BD=sinβ，由正弦定理得CD=sin（α+β）.

在△BCD中，显然BD＞CD-CB，则有sinβ＞sin（α+β）-sinα⇒sinβ＞2sinα-sinα=sinα⇒β＞α.

评注：一般来说，代数问题较为抽象，若能通过构造恰当的几何图形，将数量关系转化为几何关系，利用熟悉的数形结合这一重要的数学思想方法，往往可以增加问题的直观性，使得解答过程事半功倍、解答流程独具匠心.倘若纯粹从三角的放缩来解决案例4显得非常复杂，而构造圆则迅速获解.由此不难看出：要想构造解析几何图形，必须熟悉数或代数式所代表的几何意义，同时还要掌握几何图形的代数结构，将两者有机结合，才是由数构形的关键所在.

4.因数（方程、方程组等）构造空间解析几何图形模型

显然，d＞r⇔平面与球相离⇔方程组无实数解；d＜r⇔平面与球相交⇔方程组有无数多组实数解，这无数多组实数解正是平面截球面所得到的圆上的所有点；d=r⇔平面与球相切⇔方程组有唯一一组实数解.

案例5：试求下列三个方程所组成的方程组所有实数解：

x+y+z=3，x2+y2+z2=3，x3+y3+z3=3.

剖析：将前面两个方程分别看作平面与球面，依据点到平面的距离公式易得d=r，即平面与球面相切，即有唯一一组实数解，易得x=y=z=1，显然满足第三个方程，故该方程组所有的实数解只有一组，即x=y=z=1.

评注：华罗庚指出：“数形本是两相依，焉能分作两边飞.数缺形时少直观，形缺数时难入微.切莫忘，几何代数统一体，永远联系莫分离.”案例5是第2届美国数学奥林匹克竞赛试题，若直接解方程，撇开计算复杂不说，纵使解出也是索然无味.将它们看作平面与球，借助球心到平面的距离公式获得心旷神怡的解答！

（说明：因本文涉及图形较简单，限于篇幅，略去图形）

四、一点感悟

笔者在高中数学教学的同时一直从事奥林匹克竞赛辅导，也许因为工作需要，笔者从1990年左右开始关注数形结合，尤其对因数构形问题感兴趣.构造法是数学解题中一种富有创造性的思维方法，体现了数学思维的创造性.构造法对优化思维品质、激发创造力大有裨益，它是数学思想方法的一朵奇葩，充满着创造的智慧与优美，让人享受到数学之美.

由数构形往往获得新颖、独特、简捷的思维与解法，常常让人豁然开朗、茅塞顿开，身心得到一种极度的快感与满足.通过情感态度与价值有机结合，优化思维品质，发展智力，激发创新意识、创新精神，提高学生的创新能力，培养创造型人才.

由数思形、依数构形需要扎实的基础知识、厚实的数学功底、敏锐的观察能力、丰富的联想能力、较强的数据处理能力、较高的代数变形技巧、灵活的迁移能力、强烈的构造意识.诚然，由数构形、依数构形绝非一朝一夕，需要长期磨炼，日积月累，做用心之人（多留意）、用眼之人（多阅读）、用脑之人（多思考），功到自然成.

1.于志洪.一道哈佛入学试题趣赏［J］.数学通讯（下），2013（12）.

2.沈文选，杨清桃.数学思想领悟［M］.哈尔滨：哈尔滨工业大学出版社，2008.

3.王连笑.数学解题靠数学思想给力［M］.哈尔滨：哈尔滨工业大学出版社，2011.

4.王淼生.构造长方体巧证不等式［J］.数学通讯（下），2012（5）.

5.王淼生.妙用三角形基本性质巧解竞赛试题［J］.中学数学（上），2013（3）.A

*本文系全国教育科学规划教育部重点课题（立项批准号GOA107017）“小学生数感的发展与特征研究及课程设计”；福建省“十二五”规划2013年度课题（立项批准号：FJJKXB13—083）“优化学生思维品质的魅力数学课堂模式研究”及厦门市2013年第三批课改课题（立项批准号：Z3042）“数学构造思想方法优化学生思维品质的实践研究”的阶段性成果.