☉安徽省浮山中学 吴约中

探究与拓展一道经典数学高考题

☉安徽省浮山中学 吴约中

一、问题由来

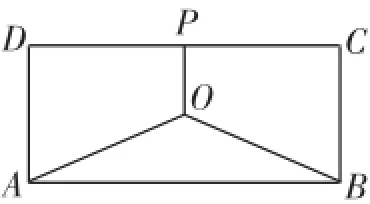
图1

题目（2008年高考数学江苏卷17题）如图1，某地有三家工厂，分别位于矩形ABCD的两个顶点A、B及CD的中点P处.AB= 20km，BC=10km.为了处理这三家工厂的污水，现要在该矩形区域上（含边界）且与A、B等距的一点O处，建造一个污水处理厂，并铺设三条排污管道AO，BO，PO.记铺设管道的总长度为ykm.

（1）按下列要求建立函数关系式：

①设∠BAO=θ（rad），将y表示成θ的函数；

②设OP=x（km），将y表示成x的函数.

（2）请你选用（1）中的一个函数关系确定污水处理厂的位置，使铺设的污水管道的总长度最短.

评析：该题为情境创设开放题，考生首先要将语言文字的理解等价化归为函数模型（变量的范围），主考函数的概念、解三角形、导数中函数最值的应用等基础知识，考查考生的数学建模能力、抽象概括能力和解决实际问题的能力；特别是第（2）问，涉及污水处理厂科学选址、有效“节能”和排污管道长度最优化问题的探究.

②若OP=x（km），则OQ=10-x，所以OA=OB=

二、问题探究

上述的点O与三角形中的费马点有何关联呢？

1.背景再现

（1）费马点定义：在一个多边形中，到每个顶点距离之和最小的点叫做这个多边形的费马点.

（2）如果三角形有一个内角大于或等于120°，这个内角的顶点就是费马点；如果3个内角均小于120°，则在三角形内部对三边张角均为120°的点，就是三角形的费马点.

（3）如何作一个三角形的费马点？

作法：①作一三内角均小于120°的△ABC.②分别以AB，AC为一边，向外侧作正△ABD与△ACE.③连接CD、BE，交于点P，则P点即为所求，如图2.

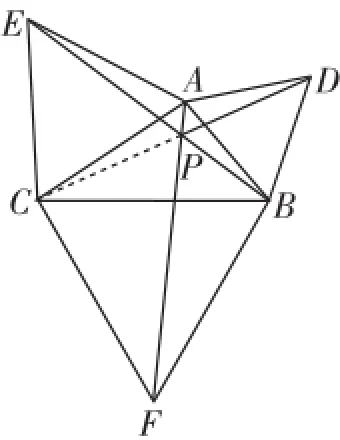
图2

（4）如何求一个三角形的费马点？

当一个三角形的最大角小于120°时，以每一个边向外侧作等边三角形，连接该等边三角形的顶点和该边的对角顶点，三条连线的交点P就是费马点.

解析：（1）由图3易知，费马点对边的张角为120°，所以△AC′C≌△ABB′，∠AC′C=∠ABB′.

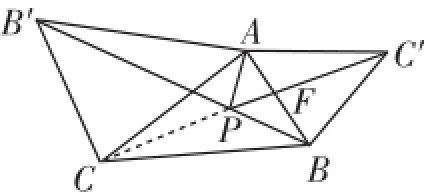
图3

又∠AFC′=∠CFB（对顶角），

所以∠FAC′=∠BPF=60°，所以∠BPC=120°.（2）PA+PB+PC=BB′.

如图4，将△APC以点C为旋转中心逆时针旋转60°与△B′DC重合，连接PD，则△PDC为等边三角形，所以∠CPD=60°.又∠BPC=120°，因此B、P、D三点在同一直线上.又∠APC=120°，所以B、P、D、B′四点在同一直线上，故PA+PB+PC=BB′.

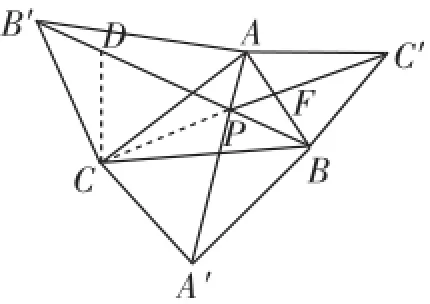
图4

（3）PA+PB+PC最短.

如图5，在△ABC内任意取一点M（不与点P重合），连接AM、BM、CM，将△AMC以点C为旋转中心逆时针旋转60°与△B′GC重合，连接BM、GM、B′G（同上），则B′B＜B′G+GM+ MB=AM+BM+CM.

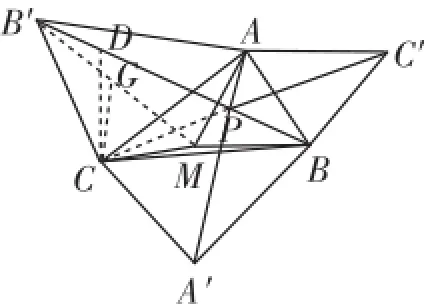
图5

所以费马点到三个顶点A、B、C的距离最短.

评注：△ABC的费马点位置是通过图形旋转，由极端原理得到的，将三边距离之和转化为同一直线上两点之间线段最短的应用.因此该道高考试题将考题和费马点有机联结，变矩形为三角形构建对应的数学模型，使问题解决更加贴近考生最近发展区，从而达到触类旁通的效果.△ABP中的点O最合适的位置是满足AO=BO且∠AOB=120°，此时同样可求得点O在AB的垂直平分线

2.题源探究拓展

探究拓展一：费马点是否适合于四边形中的优化问题？

例1A、B、C、D四个城市恰好为一个矩形的四个顶点.现要建一个公路系统，使每个城市之间都有公路相通，并使整个公路系统的总长为最小，问：该公路系统应当如何修建？

解析：如图6，连接AC，BD，交点为P，则点P到点A、B、C、D的距离之和最短.

如图7，在矩形内部任取一点Q，连接AQ、BQ、CQ、DQ.

因为AQ+CQ≥AC，BQ+DQ≥BD，则点P为最佳位置.

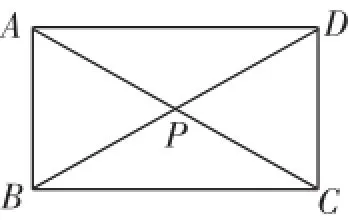
图6

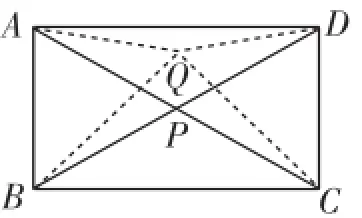
图7

探究拓展二：如果不计较结点的个数，有没有更短的线路？

如图8，在△APD、△BPC中分别作出费马点E、F（费马点定义可证三角形任意两边之和大于费马点到三顶点距离之和）.

由AP+PD＞AE+PE+DE，PB+ PC＞BF+CF+PF，得AC+BD＞AE+ PE+DE+BF+CF+PF.

又E、P、F三点共线，所以AE+ DE+BF+CF+EF＜AC+BD，即图8的连接方法是最短的.

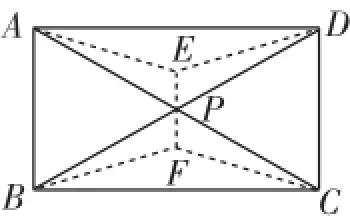
图8

评注：“公路系统总长”的优化问题，可以归结为如“亭子道路的布局设计”、“地铁运输线的设计”等，这些可以展现数学文化的外在美、和谐美等.

探究拓展三：费马点是否适合于竞赛中的代数问题？

例2设x，y，z，a，b∈R+，且a＞b，x，y，z满足条件

解析：这道代数问题似乎与费马点没有直接关系，若根据方程组的特点，构造一个特殊三角形来解.由于等式右端为a2、b2、a2+b2，因此构造一个Rt△ABC，两条直角边分别为AB=a，AC=b，∠A=90°.并在Rt△ABC内找一点O，连接OA、OB、OC，使得它们之间的夹角为120°（如图9）.设OA=x，OB=y，OC=z.由余弦定理知x，y，z，a，b之间的关系满足上述已知的方程组条件.再将△ABO绕A点逆时针旋转60°，得到△AB′O′.易知B′、O′、O、C四点共线，且B′O′=y，O′O=x，OC=z，∠B′AC=150°，即B′C=x+y+z.在△AB′C中，AB′=a，AC=b，∠B′AC=150°，则

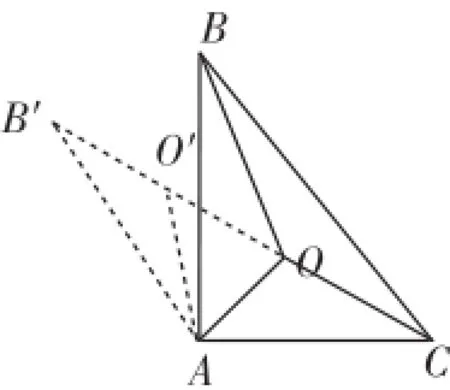
图9

评注：费马点也可以看作是一种几何模型.在一些代数问题中，建构相应的数学模型，问题就会变得非常简单.这展示了数与形的有机结合，对问题的解决、深化，效果明显.

3.思维探究拓展

思维探究拓展一：解题思维需要有“第二过程”的暴露.

数学解题思维过程的暴露是一个不断分析解题过程、循环提升理解能力的探究过程.在此过程中，既有“第一过程”的思维暴露，又有“第二过程”的思维暴露，是解题思维的全过程暴露；在内容上，既包括数学家的思维，又包括教师、学生的思维（教学课堂应是这三种思维的同时暴露）.

（1）停留在“第一过程”的思维暴露是不完整的.

解题教学中暴露数学解题思维过程、结论的发现过程、思路的探求过程、方法的提炼过程等称为“第一过程”的暴露.与解题思路的探求相比，初步解法的生成，其本身仍然是一个隐含在知识或结论中的思维过程，依然是解题者不懈努力、有效思考的真实过程.如果其解法是粗糙的，它就为我们继续探索深层结构准备了研究的素材与园地；如果其解法是深刻的，它就为我们的模仿、练习提供了范例和榜样，有利于我们直接领悟问题的深层结构.

例3如图10所示，半径为2cm，圆心角为90°的扇形OAB的A（B上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I，当点P在（上从点A运动到点B时，求内心I所经过的路径长.

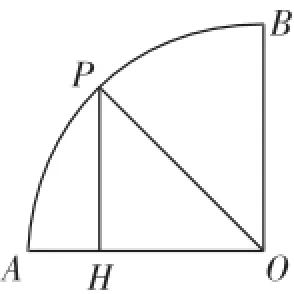
图10

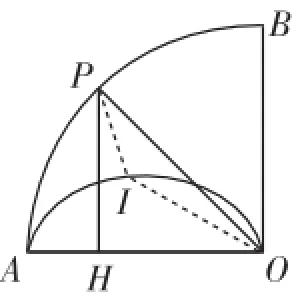
图11

解析：如图11，∠AOP与∠OPH的角平分线的交点为点I，因为∠PHO= 90°，所以∠HPO+∠HOP=90°.

由题意知，∠PIO始终等于135°，且OP的长始终等于2cm.一个角度不变，所对的一条边的长度不变，经过画图、思考，发现I所经过的路径可以看作2cm为弦，且所含圆周角为135°的一段弧.点P从点A运动到点B，如图12，I所经过的路径就是以AO为弦，且所对的另一个圆周角为45°，所以圆心

图12

（2）进行“第二过程”的思维暴露是有道理的.

解题过程中在暴露结论发现、思路探求的基础上，自觉分析、继续反思数学教学、解题的思维过程称为“第二过程”的暴露.

第一过程的暴露主要反映了将题作为对象，将解作为目的的认知活动，它实现了有序信息向大脑的线性输入，而第二过程的暴露不仅要将题作为对象，将解作为目标，而且要将包括“题与解”在内的解题活动作为对象，将智力的开发、促进人的发展作为目标，将历时性的线性材料再组织为一个共时性的立体结构.是在更高层面上的再认知活动，具有鲜明的元认知特征和具体的元认知开发实效，思维的广阔性、灵活性、深刻性、批判性等品质都将得到有效的锻炼和提升.通过揭示为题的深层结构，对学生隐性的数学领悟施加显意识的影响，为数学直觉的诱发铺设必要的逻辑通道，产生协同效应.

思维探究拓展二：典型例题的探究拓展是一种案例研究.

在上面的解答过程中，思维很是精妙，结果又耐人寻味，似乎不必用到∠AOB=90°.如果∠AOB不是90°，那么还能求解吗？上面的求解是不是有破绽呢？于是又进行了下面的探究.

问题1：如果∠AOB＜90°，例如∠AOB=60°，如图13所示，那么

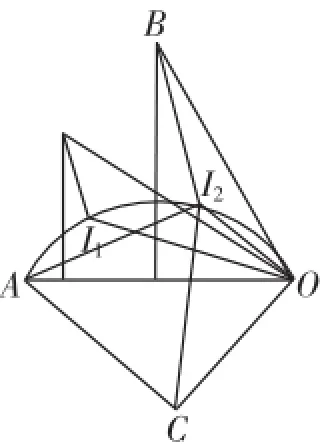
图13

问题2：如果∠AOB＞90°，例如∠AOB=120°，如图14所示，内心I的路径长为A（O与O（I的和，与问题1相似，同理可得∠ICD=∠BOD= 180°-∠AOB=60°，∠OCD=90°，所以∠OCI=30°.

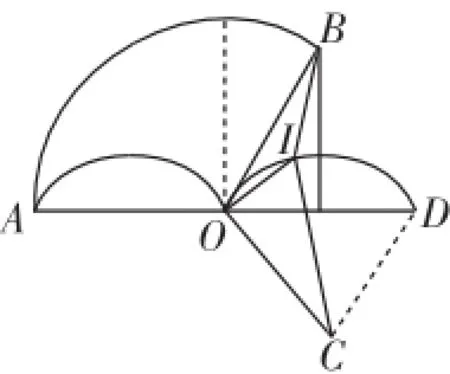
图14

这道题的解题方法非常巧妙，动态弦转化定弦，通过这样一转化，就解决了这个问题.再经过深入分析，不管∠AOB为多少度，都能求出这种三角形内心的路径长.而在分析思考的过程中，开发、提升了学生的思维.

数学解题案例渗透着对特定数学问题的深刻反思，反映了数学解题实践的经验与方法，蕴含着一定程度的理论原理，是了解解题教学的窗口，是数学解题理论的故乡，是数学教师发展的阶梯.数学解题是智慧创造活动.谁也无法教会我们所有的题目，重要的是，通过有限道题的解题分析、案例研究、探究拓展来领悟解无限道题的数学机智.

人生有尽，题海无涯；思维有路，探究无限，探究拓展高考数学题的目的就是要通过有限个问题的思考去领悟无限个问题的思维方法.课堂是教师教学的实践场所，是教师成长和发展的主阵地，是教师生命价值得以提升的现实起点，实践情境和经验背景构成了教师构建知识的专业场所.以教学中面临的各种具体问题为研究对象，既注重实际问题，又注重概括提升、总结经验和探究规律，一方面有助于教师数学思想的启迪，数学人文精神的培育，数学情趣、意志、风格的塑造，另一方面又有助于构建体现新课程理念的教学模式与教学风格，有助于形成驾驭新课程教学的有效经验和教育智慧，使学生从中受益，从而提高他们的创新意识和创新能力.解题不回顾，如同走进宝山空手回，作为一个平凡的数学教育工作者，笔者想通过这样的探究拓展，期望学生以研究的观点去对待解题，将每一次解题当作对数学真理的一次探究和再发现过程.解题之后若善于进行命题的引申、探究与拓展，对优化学生的思维品质，增强学生提出问题、分析问题与解决问题的基本技能会有所帮助；希望成为学生思维火把的引燃者；希望自己的学生都成为会学习、会思考、会探究、会拓展的学海弄潮儿.

1．罗增儒，著.数学解题学引论［M］.西安：陕西师范大学出版社，2001.

2．［美］G.波利亚，著.怎样解题［M］.涂泓，冯承天，译.上海：上海科技教育出版社，2007.

3．［苏］费里德曼，著.怎样学会解数学题［M］.梁法驯，译.哈尔滨：黑龙江科学技术出版社，1981.F