Xishan Zhang,Kaoli Huang,Pengcheng Yan,and Guangyao Lian

1.Ordnance Engineering College,Shijiazhuang 050003,China;

2.Ordnance Technological Research Institute,Shijiazhuang 050003,China

Hierarchical hybrid testability modeling and evaluation method based on information fusion

Xishan Zhang1,*,Kaoli Huang2,Pengcheng Yan2,and Guangyao Lian2

1.Ordnance Engineering College,Shijiazhuang 050003,China;

2.Ordnance Technological Research Institute,Shijiazhuang 050003,China

In order to meet the demand of testability analysis and evaluation for complex equipment under a small sample test in the equipment life cycle,the hierarchical hybrid testability modeling and evaluation method(HHTME),which combines the testability structure model(TSM)with the testability Bayesian networks model(TBNM),is presented.Firstly,the testability network topology of complex equipment is built by using the hierarchical hybrid testability modeling method.Secondly,the prior conditional probability distribution between network nodes is determined through expert experience.Then the Bayesian method is used to update the conditional probability distribution,according to history test information,virtual simulation information and similar product information.Finally,the learned hierarchical hybrid testability model (HHTM)is used to estimate the testability of equipment.Compared with the results of other modeling methods,the relative deviation of the HHTM is only 0.52%,and the evaluation result is the most accurate.

small sample;complex equipment;hierarchical hybrid; information fusion;testability modeling and evaluation.

1.Introduction

The testability analysis and evaluation of equipment is an important step in the course of equipment development. Testability analysis and evaluation should be based on mass data of equipment.But the size of the test sample is small due to the complex structure and high cost,therefore,it is difcult to obtain effective results using traditional statistical methods of big sample data[1,2].At the same time,kinds of testability experiments will be carried out in the development process of the complex equipment,consequently,a large amount of subsystem test information will be produced.In addition,there are similar product information and expert experience information available.As a result,how to establish an effective testability model using these prior information and improving the accuracy of testability evaluation is an urgent problem [3–5].

As we know the cost of testability experiment is high, the amount of samples is small,so the achieved testability analysis is an estimation and decision making problem based on small samples and uncertainty information. In that case,a testability analysis and evaluation method based on Bayesian network inference was proposed in[6–9].Meanwhile,in[10],a diagnostic Bayesian network modeling method based on multi-signalow graphs was proposed in order to deal with small samples and conicting evidencein diagnosis of complexequipment.Owing to the small sample characteristics of the momentum wheel, the large sample experiments to assess its reliability are difcultto carryout.But thereis a great deal of priorinformation obtained from specialists and ground testing,so in [11,12],a new reliability modelingand assessment method using Bayesian network was proposed.There are small samples and zero failure characteristics in space bearing reliability modeling and analysis,a hierarchy Bayes modeling and analysis method was proposed in[13]to solve the difculties under small sample circumstances.In[14], an improved Bayesian approach in assessment of weapon performance was proposed,when weapon test data were insufcient.How a hierarchical Bayesian statistical framework can make better use of ecological studies for applied riskassessments whendata arelimitedwas showedin[15].

We can see that Bayesian network can make full use of prior information and play a role of learning in the testability analysis to reduce the size of test samples,save development cost,and shorten the development cycle[16]. However,the testability model using Bayesian network cannot be established in the early stage of the equipment design,therefore,its application is limited.

To establish a testability analysis and evaluation model with small samples in the equipment life cycle,thehierarchical hybrid testability modeling and evaluation (HHTME)method is proposed,which combines the testability structure model(TSM)with the testability Bayesian network model(TBNM).The hierarchical hybrid testability model(HHTM)not only has capability of dealing with uncertainty information with small samples,but also can reect the basic physical structure and function information of the equipment,therefore,this model can easily establish the testability model in the equipment life cycle.

2.HHTME method combining TSM with TBNM

2.1Theoretical foundation of HHTME

By using deep knowledge,both the TSM and TBNM do well in testability modeling in some aspects for a system, but its application is limited[17].The testability analysis and evaluation model of the complex system established from the equipment fault diagnosis perspective focuses on looking for the fault root of the measured object.According to the needs of testability analysis and evaluation,the HHTM for the complexsystem is established fromthe perspectives of its structure,function,failure and behavior, which refers to the method of directed graph modeling, and combines TBNM with TSM.The main elements of the model are shown in Fig.1.

Fig.1 Main elements of testability model

(i)Inordertobuildthetestability evaluationmodelfrom its system structure,therst main considerations are the strong structural relevance of the complex system,and propagation characteristics of complex system failures,so it is convenient for fusing multivariate information to locate the fault source through the testability model built by its internal relationship.Secondly,the testability model built by the system structure is very clear,which is easy to build the testability model.

(ii)Modeling from the perspective of system failures is an important aspect to build the testability evaluation model.The system structure,behavior and function are related with the system failure.Failures belong to different levels of the system and they spread among system units by its relationship.On this basis,the failure propagation model can be built among different levels of a system.

(iii)System behavior is the external representation of a system and all system changes can be detected,which includes the behavior changes of components or the deduced behavior changes.When a system fault occurs,it will be manifested from behavior characteristics.Different failures correspond to different behavior changes,so that the different types of failures can be obtained from the different behavior changes.

(iv)System function is affected by the system fault.In the early stage of the equipment design,the test is generally dened in accordance with the system function and then in the detailed stage of the equipmentdesign,the fault correlation model can be built after the equipment failure modes are determined.

2.2Ideas of HHTME

The testability model for equipment is the basis of the testability design and analysis.The ideas of the HHTME are as follows:

(i)In order to have a good observation in the testability design and analysis,and then facilitate fault diagnosis and trouble shooting in the using of equipment,the testability model can not only reect the basic physical structure and function information of equipment,but also describe the logical relationship between the failures and tests,and the test resources utilization relations.

(ii)Due to the test uncertainty,the testability model should not only have the capability of expressing and reasoning the uncertainty information,but also fuse multisource testability information to analyze and evaluate the testability quantitatively.

(iii)Testability modelingfor complexequipmentshould be layered.In order to reduce the difculty of modeling, the testability model of the whole equipment should be composed preferably by small fragments of the testability model of the subsystem or the function module.It has advantages of extending and modifying the testability model to facilitate reuse.

Therefore,the basic elements of the testability model are the equipment unit subsetthe failure modes subsetthe test subsetthedirectededgesubset E,andtheconditional probability between nodes subset P.The HHTM formalized description can be expressed as HHTM= (C,F,T,E,P),and the detailed description of its con-stituent elements are as follows:

(i)The equipment unit subset C:C={c1,c2,..., ci,...,cm},where ci(1≤ i≤ m)represents the constituent unit i.The correlation between the constituent units can be expressed as CC={cicj},where cicj=〈ci,cj〉represents the correlation between the constituent unit ciand cj(ci,cj∈C).

(ii)The failure modes subset F :F ={f1,f2,..., fi,...,fn},where fi(1≤ i≤ n)represents the failure mode i.The afliation relationship between the failure modes and the constituent units can be expressed as CF={cifj},where cifj=〈ci,fj〉represents the afliation relationship between the constituent unit ciand the failure mode fj(ci∈C,fj∈F).

(iii)The test subset T :T ={t1,t2,...,ti,...,tl}, where ti(1≤i≤l)represents the test i,each test is binary,namely“pass”and“not pass”.The mappingrelationship between the failure modes and the tests can be expressed as FT={fitj},where fitj=〈fi,tj〉represents the mapping relationship between the failure mode fiand the test tj(fi∈F,tj∈T).

Fig.2 Steps of HHTME

(iv)The directed edge subset E={efitj,efkfl,etgth}, where efitjrepresents the informationow between the failure mode fiand the test tj,efkflrepresents the informationow between the failure mode fkand the failure modefl,andetgthrepresentstheinformationowbetween the test tgand the test th;

(v)The conditional probability between nodes subset P:P={FDij},where FDijrepresents the abnormal probability of tjwhen fiis abnormally monitored by tj.

In addition to the above basic elements,the HHTM also includes the following elements:

(i)The system function subset G:G={g1,g2,..., gi,...,gk},wheregi(1≤i≤k)representsthe functioni. The affect relationship between the failure modes and the functionscanbe expressedas FG={figj},wherefigj=〈fi,gj〉represents the affect relationship between the failure mode fiand the function gj(fi∈F,gj∈G).

(ii)Thefailureratesubset λ={λ1,λ2,...,λi,...,λn}, where λirepresents the failure rate of failure mode i.

(iii)The correlation matrix D:D=[dij]is of m×n dimension,where dijrepresents the correlation between the failure mode fiand the test tj.

(iv)UnitlevelsofthesystemL={l1,l2,...,li,...,lm}, where lirepresents the level i,and the larger the i,the lower the level.

2.3Steps of HHTME

Step 1Clear modeling object.Firstly,carry out the analysis in the schematic diagram model,the testability structure model,the failure mode,effects and criticality. Then identify and extract the information of equipment composition,function,failure modes and test information. Finally,clear the interact inuence between the subsystem and components of equipment.

Step2Hierarchicalhybridtestabilitymodeling.Firstly,establish a small fragments testability model for the subsystem or the function module by analyzing the relationship between failures and tests.Then connect each submodel to establish the HHTM for the whole equipment system,on the basis of the relationship of failure modes propagation and the function structure.

To facilitate testability evaluation,according to the accessibility analysis,change the HHTM into the testability Bayesian networkmodel and analyzethe conditionalprobability between nodes.

Step 3Testability model validation.To adjust,revise and check the established HHTM,evaluate the accuracy of the HHTM by consulting experts in theeld.

Step 4Testability analysis and evaluation for equipment.After the establishment of the testability model,rstly,expert experiencecan be used to determine the conditional probability distribution between network nodes. Then the Bayesian inference can be used to update the conditional probability,according to the history test information,the virtual simulation information and the similar products information.Finally,the learned HHTM is used to estimate the testability of equipment.

Here is an example to illustrate this modeling process. A system consists of two function modules c1and c2,and there are seven failure modes f1,f2,f3,f4,f5,f6,f7,andve tests t1,t2,t3,t4,t5.The HHTM fragmentof function module c1is shown in Fig.3,which is established by the hierarchical hybridtestability modeling method.The function module c1has four failure modes f1,f2,f3,f4,and three tests t1,t2,t3.

Fig.3 Model fragment of function module c1

The model fragment of c2is shown in Fig.4,which is established by the hierarchical hybrid testability modeling method.The c2has three failure modes f5,f6,f7,and two tests t4,t5.

Fig.4 Model fragment of function module c2

After the model fragments of each function module are established,each model fragment is linked together to establish the HHTM of the whole system by the fault propagation,as shown in Fig.5.The failure modes f1,f2,f3of c1cause the failure modes f5,f6,f7of c2to occur respectively.

Fig.5HHTM

The process of the hierarchical hybrid testability modeling for equipment is shown in Fig.6.

It needs to build up the correlation between the failure modes subset and the tests subset based on fault propagation characteristics to facilitate the testability evaluation. Accordingto the model transformationsteps,rstly,determine the unit state nodes and generate the observed nodes. Thenestablishtherelationshipbetweentheunitstatenodes and the observed nodes by the connection relationship of the HHTM.Finally,transform the HHTM into the TBNM, as shown in Fig.6.

Fig.6 Process of the hierarchical hybrid testability modeling

3.Representation of HHTM based on information fusion

3.1Representation of HHTM based on relationship matrix

The representation method of the testability model is divided into the graphical method and the matrix method. The testability model established by the above modeling ideas and modeling steps is the graphical model.Besides, thereareothermodels,suchas theinformationowmodel, the multi-signalow graph model and the hybrid diagnostic model.According to the information of the graphical model,the relationship between failure modes and tests can be extracted to establish the relationship matrix which is the mathematical representation of the relationship between failure modes and tests for the modeling object, and the foundation of testability analysis and evaluation for complex equipment.The relationship matrix of failure modes and tests is dened as follows[18]:

Matrix elements

where i=1,2,...,m,j=1,2,...,n.The row vector represents the correlation between the corresponding failure and each test,and the column vector represents the correlation between the corresponding test and each failure.

According to the accessibility analysis,the relationship between failure modes and tests is shown in Table 1.

Table 1 Relationship matrix between failure modes and tests

3.2Failure rate estimation based on Gamma distribution

For the life of the equipment obeys exponential distribution,the Gamma distribution is usually taken as the prior distribution of failure rates,which is shown as[19]

In the early stage of the equipmentdesign,dueto the absence of the reliability test data,the failure rate prior information is often obtained by experts specialized in equipment reliability design and analysis.The level of the failure rate can be determined accurately by understanding the regularity of the failure rate.The following method solvesthe superparametersa andbthroughdifferentquantiles of Gamma distribution.Firstly,according to the commissioning data of equipment in the development stage, combining with the reliability expert experiences,the failure rate magnitude K and corresponding condence levels C1and C2when the failure rate takes the extreme minimum value LL,and the maximum value UL are obtained.Then the super parameters of Gamma distribution are worked out by the following formula[20]

Fig.7 shows the probability density function curve of Gamma distribution under different parameters.

Fig.7 Probability density function curve

The average value of Gamma distribution can be acted as the point estimate of the failure rate

Theestimationvalueofthefailureratein Fig.5obtained by the above method is shown in Table 2.

Table 2 Failure rate estimation values 10−6

3.3Determined prior distribution of conditional probability based on expert experience

The nodes of the HHTM have two states.According to the inference of the Bayesian,Beta distribution is usually takenas thepriordistributionofthe conditionalprobability P,denoted by Beta(P;α,β).The failure detection rate of the nodes is set as P,and the correspondingprior distribution is shown in the following formula[21]

α and β are the super parameters of Beta prior distribution.It is the key to determine the values of α and β when thepriordistributionformis known.Theaveragevalueand variance of the fault detection rate are shown as follows:

According to the Bayesian network learning algorithm, the conditional probability between nodes is determined by success or failure test data.However,it has no enough testability test data to determine the super parameters of Beta(P;α,β)distribution in the early stage of the equipment design.Therefore,the expert experience information is used to determine the super parameters of prior distribution.If there have n experts,the expert i assessment for the evaluated object is expressed by the trapezoidal fuzzy number[22–24],and the credibility is δi,then the judgment trapezoidal fuzzy numbers of n experts can be obtained:According to the credibility of each expert,the weight of each expert can be dened as follows:

According to the addition algorithm of fuzzy numbers,

The fuzzy number can be obtained after n experts assessment weighted.

The prior value and variance of failure detection rate P can be obtained based on the expert experience information after removing the fuzzy value from the trapezoidal fuzzy number(e,f,g,h).

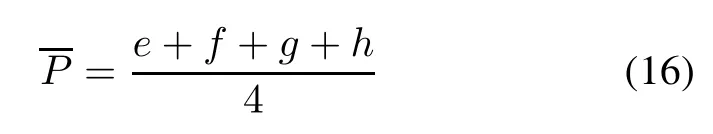
The variance as the goal,the average value as the constraint,uniting(11),(12),(16)and(17),the super parameters α and β which describe the prior information can be solved by using the following optimization model

where E(P)is the average value of Beta(P;α,β)distribution,and V(P)is the variance of Beta(P;α,β)distribution.The priordistributionof the conditionalprobability P between nodes for the HHTM established in Fig.5 is shown in(19)by using the above method.

3.4Posterior distribution of conditional probability between nodes determined

A large amount of test information is accumulated in the development,productionandusing ofcomplexequipment, such as history test information of the sub-system,virtual simulation information and similar products information. The Bayesian theory is used,through fusing the prior distribution and the sample data X to obtain posterior distribution,and the formula is as follows[25,26]:

where π(P)is the prior distribution,π(P|X)is the posterior distribution after fusing test sample X,and f(X|P)is the probabilitydensity functionof test sample X underthe given testability parameter P.

Any failure mode associated with test tiis injected into the equipment,such as the failure mode fj,then repeat tiNitimes,and add up the number of pass times.The test data are shown in Table 3.

Table 3 Testability test data

Based on the test data,the Bayesian network learning steps are as follows:

Step 1Determin the prior distribution of the conditional probability between nodes.The prior distribution of the conditional probability can be described as the following Beta distribution

Step 2The probability density function of Piis determined by the sample data Xi.

Step 3Equations(21)and(22)are plugged into(20) to obtain posterior distribution.

According to the Bayesian network learning,the posterior distribution of the conditional probability between nodes in Fig.5 is shown as

4.Testability evaluation for complex equipment based on the HHTM

After establishing the HHTM for complex equipment,the analysis and evaluationcan be carried out by Bayesian network inference.

4.1Testability evaluation under the condition of no test data

There is no available test data that can be used in the early stage of the equipment design.The estimation of the conditional probabilitybetween nodes can be obtained by(19) based on the experts experience information as follows

The fault detection rate under the single failure condition can be obtained by the conditional probability matrix from Bayesian network.Corresponding to each failure mode,several different test signals may appear,and the fault detection rate of single faults should be measured by the detection rate of all correlation tests.The fault detection rate of single failures can be obtained through the Bayesian theory.

Then the equipment fault detection rate can be dened as follows:

The point estimation value of the conditional probability between nodes under the condition of no test data is plugged into(25),and each fault detection rate can be obtained as follows:

Similarly,we have

The faultdetectionrate ofequipmentcan beobtainedby (26)as

4.2Testability evaluation under the condition of having test data

The point estimation value of the conditional probability between nodes under the condition of having test data can be obtained by(24).

According to the above method,the fault detection rate of equipment is FDR=0.976.

4.3Evaluation results analysis

The calculation results of the different methods are shown in Table 4.

Table 4 Analysis results of different methods %

Fromthecontrastiveanalysisoftheresults,we canlearn that

(i)Comparingwithothermodelingmethods,theHHTM can not only handle testability uncertainty information with small samples,but also be able to reect the relationships of the structure and fault propagation among equipment modules.

(ii)With the exception of establishing the testability model in the equipmentlife cycle,throughcomparingwith other modeling methods,the relative deviation of the hierarchical hybrid testability modeling method result is only 0.52%,so the evaluation result is the most accurate.

(iii)The results of the HHTM inference are more close to the achieved testability than other inferences.

5.Conclusions

Because the test sample size of the complex equipment is small,the test data are not sufcient and the condence level of the evaluation result is low,a new testability modeling and evaluation method of the HHTM for complex equipmentis proposed.TheHHTM cannot onlyreectthe relationships of the structure and analyze the fault propagation between equipment modules,but also be able to handle testability uncertainty information with small samples.Meanwhile,this method can make full use of the prior information in the equipment life cycle,such as history test information,expert experience information,similar products information and virtual simulation information,to evaluate the testability of complex equipment reasonably.The examples show that the method is feasible and effective.

[1]T.M.Li,C.H.Hu,X.Zhou.Research on testability integrated evaluation model based on Bayes inference theory of dynamic population and analysis of the robustness.Journal of Mechanical Engineering,2012,48(6):180–186.

[2]K.Manuel,A.S.Werner.Sharpening Wald-type inference inrobust regression for small samples.Computational Statistics and Data Analysis,2011,55(8):7–16.

[3]H.B.Yang,H.Cai,S.F.Zhang.Evaluation ofmissileguidance precision based on hybrid prior distribution.Acta Aeronautica et Astronautica Sinica,2009,30(5):855–860.

[4]H.J.Lei,K.Y.Qin.Bayesian method for determination of testability demonstration test scheme.Systems Engineering and Electronics,2012,34(12):2612–2616.(in Chinese)

[5]H.Z.Chen,Y.M.Lu,L.Wang,et al.Analysis of dynamic acoustic emission signals using multivariate statistical technique for smaller dataset.Journal of Vibration,Measurement &Diagnosis,2013,33(2):199–203.

[6]G.Y.Lian,K.L.Huang,et al.Study of testability measurement method for equipment based on Bayesian network model.Systems Engineering and Electronics,2009,20(5): 1017–1023.(in Chinese)

[7]X.W.Wang,B.Sun,Y.J.Lu,et al.Model and analysis of system testability based on Bayesian networks.China Measurement&Test,2011,37(5):90–93.

[8]C.G.Wang,X.D.Zhou,X.W.Wang.Testability evaluation for complex equipment based 0n Bayesian networks.Journal of Electronic Measurement and Instrument,2009,23(5):17–21.

[9]H.Xu,B.L.Wang,J.H.Wu.Testability prediction method base on Bayesian networks.Journal of Projectiles,Rockets, Missiles and Guidance,2007,27(4):232–239.

[10]J.Dai,J.S.Yu,P.Zhang,et al.Diagnostic Bayesian networks modeling based on multi-signalow graphs.Journal of Beijing University of Aemnautics and Astmnautics,2009,35(4): 472–475.

[11]H.T.Li,G.Jin,Z.B.Zhou.Momentum wheel reliability modeling and assessment using Bayesian network.Systems Engineering and Electronics,2009,31(2):484–488.(in Chinese) [12]H.T.Li,G.Jin,Z.B.Zhou.Bayesian networks application momentum wheeh’s to reliabilityanalysis of ground test.Journal of Aerospace Power,2009,24(6):1321–1325.

[13]G.Jin.Performance reliability modeling and estimation for space bearing under small sample circumstance.Journal of National University of Defense Technology,2010,32(1):133–137.

[14]Q.M.Li,H.W.Wang,J.Liu.Small sample Bayesian analyses in assessment of weapon performance.Systems Engineering and Electronics,2007,18(3):545–550.(in Chinese)

[15]J.M.Diez,P.E.Huime,R.P.Duncan.Using prior information to build probabilistic invasive species risk assessments. Biological Invasions,2012,14(3):681–690.

[16]Y.T.Mustafa,P.E.Van Laake,A.Stein.Bayesian network modeling for improving forest growth estimates.IEEE Trans. on Geoscience and Remote Sensing,2011,49(2):639–644.

[17]G.Y.Lian,K.L.Huang,R.Guo,et al.Research on testability based on design and analysis technology model.Systems Engineering and Electronics,2007,29(10):1777–1780.(in Chinese)

[18]J.Dai,P.Zhang,X.S.Li,et al.Novel approach for aviation electromechanical system testability modeling and analysis. Acta Aeronautica et Astronautica Sinica,2010,31(2):277–284.

[19]Y.J.Jiang,Z.Q.Yan,H.W.Xie.The method of Bayesian reliability evaluation based on mixed gamma distribution.Computing Technology and Automation,2010,29(1):106–109.

[20]T.M.Li,J.Qiu,G.J.Liu.Allocation plan of failure samples based on failure rate in testability.Acta Aeronautica et Astronautica Sinica,2009,30(9):1661–1665.

[21]R.Mathias.Empirical behaviour of tests for the beta distribution and their application in environmental research.Stochastic Environmental Research and Risk Assessment,2011,25(1): 79–85.

[22]D.Z.Zhao.Model of fuzzy prediction for gas turbine engine reliability during early design.Thermal Turbine,2012,41(2): 160–164.

[23]X.B.Zheng,G.M.Chen.New comprehensive evaluation model based on fuzzy arithmetic operations.Systems Engineering and Electronics,2004,26(12):1905–1908.(in Chinese)

[24]C.Zhang,C.B.Ma,Y.L.Hu,et al.The reliability analysis and evaluation for small sub-sample weapon system based on trapezoidal fuzzy number.Journal of Projectiles,Rockets, Missiles and Guidance,2006,26(2):128–130.

[25]H.Zhou,X.P.Zhao,W.J.Wu.Studyonthemethod oftestability assessment of some based on Bayes theory.Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(3):253–256.

[26]C.H.Chang,J.P.Yang,L.Hu.Study on testability evaluation method for complex equipment based on Bayes theory.Fire Control&Command Control,2012,37(11):173–176.

Biographies

Xishan Zhang was born in 1987.He is a Ph.D. candidate in test techniques at Ordnance Engineering College.He also holds his M.S.degree of vehicle engineering from the same college.His research interests include testability design analysis and verication.

E-mail:xishan871026@sina.com

Kaoli Huang was born in 1958.He received his Ph.D.degree from Nanjing University of Science and Technology in 2004.Now he is a researcher in Ordnance Technological Research Institute.His research interests include design for testability,automatic test and fault diagnosis.

E-mail:756052193@qq.com

Pengcheng Yan was born in 1965.He received his Ph.D.degree from Huazhong University of Science &Technology in 2011.Now he is a researcher in Ordnance Technological Research Institute.His research interests include design for testability,automatic test and fault diagnosis.

E-mail:zongtiban@163.com

Guangyao Lian was born in 1980.He received his Ph.D.degree from Mechanical Engineering College in 2008.Now he is a engineer in Ordnance Technological Research Institute.His research interests include design for testability,automatic test and fault diagnosis.

E-mail:lianguangyao@163.com

10.1109/JSEE.2015.00060

Manuscript received October 10,2014.

*Corresponding author.

This project wassupported by the National Defense Pre-research Foundation of China(51327030104).