Yong Wu,Jun Wang,Xiaoyong L¨u,and Yunhe Cao

National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China

Yong Wu*,Jun Wang,Xiaoyong L¨u,and Yunhe Cao

National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China

In order to deal with the particle degeneracy and impoverishment problems existed in particlelters,a modied sequential importance resampling(MSIR)lter is proposed.In thislter,the resampling is translated into an evolutional process just like the biological evolution.A particle generator is constructed,which introduces the current measurement information(CMI)into the resampled particles.In the evolution,new particles arerst produced through the particle generator,each of which is essentially an unbiased estimation of the current true state.Then,new and old particles are recombined for the sake of raising the diversity among the particles.Finally,those particles who have low quality are eliminated.Through the evolution,all the particles retained are regarded as the optimal ones,and these particles are utilized to update the current state.By using the proposed resampling approach,not only the CMI is incorporated into each resampled particle,but also the particle degeneracy and the loss of diversity among the particles are mitigated,resulting in the improved estimation accuracy.Simulation results show the superiorities of the proposedlter over the standard sequential importance resampling(SIR)lter,auxiliary particlelter and unscented Kalman particlelter.

sequential importance resampling(SIR),evolution, current measurement information(CMI),unbiased estimation.

1.Introduction

Generally,a better importancedensity function(IDF)or resampling approach is designed to overcome the particle degeneracy and impoverishment problems.The choice of IDF is of importance for particlelters.In the SIR,the transition density function is utilized for the IDF to generate random particles,and the current measurement information(CMI)is only used to assess the quality of each particle,which is a potential shortcoming of SIR.From the optimal IDF[7,8],we can see that the CMI should be incorporated into the sampled particles.Inspired by this idea,Merwe et al.proposed the unscented Kalman particlelter(UPF)[9],where the unscented Kalmanlter was used as the IDF.In some applications where the measurement noise is small,the UPF outperforms the SIR,howeverit has muchhigher computationalcomplexity.Pitt and Shephard proposed the auxiliary particlelter(APF)[10] where an extra variable was introduced.Thislter can be regardedas resampling at the previous time index by using the CMI,and it performs well in the case of small process noise.Actually,the IDF is difcult to design.On the other hand,the resampling is another option to overcome the two problems.An effective resampling approach can not only move particles towards regions of high likelihood wherethetruestate lies withhighprobability,butalso keep the diversity among the particles.Arulampalam et al.pre-sented the regularized particlelter(RPF)[7],which resampled from a continuous approximation of the posterior PDF,to improve the performance of the SIR.Though the performanceofthe RPF is betterthantheSIR in thecase of small process noise,the particle impoverishment problem is still very severe.In[11],the difference evolution was introduced into the resampling stage to raise the diversity among the particles,but it did not evidently improve the quality of resampled particles.

To alleviate the degeneracy problem and avoid the loss of diversity among the particles,a modied sequential importance resampling(MSIR)lter is proposed in this paper.It is identical to the SIRlter besides the resampling stage.In the resampling stage,a particle generator(PG)is constructed by maximizing the likelihood function to generate new particles repeatedly,and then differentparticles are recombined by adjusting a predened parameter,nally,the low-quality particles are eliminated.In brief,the new resamplingprocess consists of reproduction,recombination and elimination of particles.By using the PG,both the CMI and predictive information of the current state are incorporatedintotheresampledparticles,whichreducethe extentofparticledegeneracy.Moreover,therecombination and elimination raise the diversity among the particles.As a result,the MSIR has better performance.

The structure of this paper is as follows.Section 2 briey reviews the SIR.Section 3 describes the detailed procedures of the MSIR.Several discussions about the MSIR are given in Section 4.Section 5 shows the performance of the MSIR by two examples.Conclusions are drawn in Section 6.

2.Brief review of SIR

Consider the following dynamic state-space(DSS)model:

where xkand ykdenote the m-dimensional state term and n-dimensionalmeasurementtermat instantk,respectively. The process noise γk−1and measurement noise vkare zero-meanrandomvectorswith givencovariancematrices. f(·)and h(·)stand for state and measurement functions, respectively.The purpose ofltering is to employ all the measurementsuntil time k,i.e.,with the state at time k–1 together to estimate the posterior PDF p(xk|y1:k)of the state at instant k.

According to the Bayesian statistical theory,the SIR is a discrete integral method for implementing the recursive estimation ofp(xk|y1:k).Ineach estimation,p(xk|y1:k)is approximated by the random particles with corresponding weights as

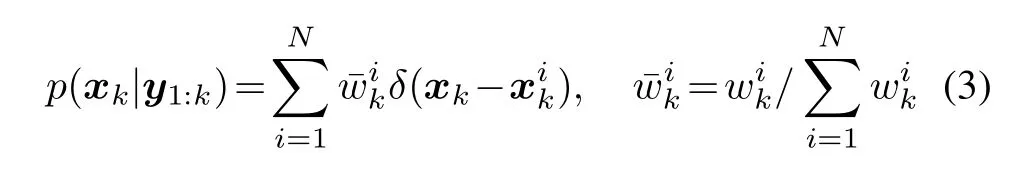
where δ(·)is the Dirac delta function,N is the total number of particles,denotes the particle sampled from the IDFis the associated normalized weight of the ith particle andis the correspondingnonnormalized weight,which is recursively updated by

Then the resampling is performed to reduce the effects of the particle degeneracy.After the resampling,each particle has the same weight.Finally,the state estimate is conducted,i.e.

3.Modifed SIR

From the previous descriptions of the SIR,we can see that there exist two problems in the SIR.(i)The sampled or resampled particles only contain the predicted information about the state,and the CMI is not fully utilized.In the case of small observationnoise,i.e.,the shape of p(yk|xk) is very sharp,the number of particles lying in the areas of high likelihood is small,which leads to severe particle degeneracy.(ii)Because the particles with high weights are duplicated many times,the resampled particles contain largenumbersof repeatedones.This results in a loss of the diversity among the particles and serious particle impoverishment.

In this paper,we try to overcome the problems stated above by introducing the CMI and the idea of biological evolution into the resampling stage.The detailed process of the proposed MSIR is described as follows.

In the MSIR,the transition density function is still used as the IDF.We denoteas the predicted particles sampled from the IDF,i.e.,

Assume the measurement noise is subject to Gaussian distribution(0,R).Under this assumption,the likelihood function p(yk|xk)is written as

After obtaining the predicted particles,the reampling is performed.Generally,the CMI is utilized to improve the performance of the SIR.Inspired by this idea,the current measurement ykis incorporated into the resampled particles to improvethe quality of the particles and mitigate the particledegeneracybymaximizingthelikelihoodfunction, that is,

Equation(9)denotesan unconstrainedmaximizationproblem,and it is equivalent to the following one:

Tosolvetheproblem,h(xk)isapproximatedbyexploitingrst-orderTaylorseriesaroundwhichdenotesaprediction of the true state xkas

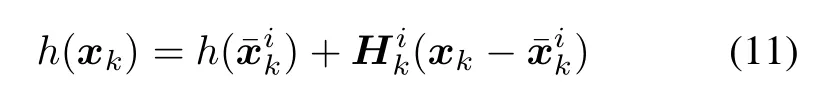
where

By substituting(12)into(10),we can obtain

Obviously,(14)is a linear equation about xk.Solving it, xkcan be represented by

Then,an evolution is performed,which is actually an iterative process of reproduction,recombination and elimination of particles.Letbe the current and derivative particles,respectively,where g=1,...,G and G is the maximum number of iterations.The initial evolutional particles are the same as the predicted ones sampled from the IDF,The derivative particles are generated by the PG,i.e.,

Next,in order to increase the diversity of particles,the current and derivative particles are recombined as follows:

where F(·)is a Heaviside function,is a random number drawn from U(0,1)and Pa is a predened parameter(called recombination coefcient)which lies between 0 and 1.A small Pa such as 0 means that the recombination is negligible.This parameter is set by specic applications.Following the recombination is elimination.To evaluate the adaptability of each recombinedparticle(RP), another new set of particles,called normative particles,are generatedby utilizingthe similaritybetweendifferentRPs, and they can be represented as

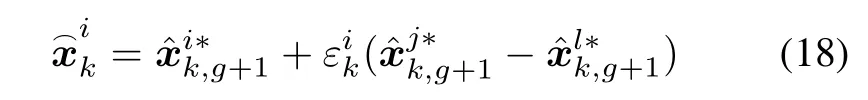
where j,l are two random integers between 1 and N.is a random number drawn from U(0,1).The adaptability of each RP is expressed asmeans the adaptability ofis less than thatshould be eliminated.The elimination is dened as

When the iterative index g reaches the maximum G,the entire evolutional course is completed.The latest particles are considered as the optimal ones,and their weights are computed by using(5).LetThen,we use these particles with the corresponding weights to estimate the state xk,that is

In summary,prediction,evolution and estimation comprise the MSIR.Among the three parts,the evolution is the most signicant one,which moves the predicted particles to the regions of high likelihood gradually.The detailed procedures of MSIR are summarized as follows.

Initialization:k=0

For k=1,2,...

(i)Prediction step

(ii)Evolution step(resampling)

Set initial evolutional particles

For g=1,2,...,G

Generate derivative particlesusing(16);

Assess and eliminate particles according to (18)–(20);

End for

(iii)Estimation step

Calculate associated weights using(5)and normalize them;

Estimate the current state xkusing(21);

End for.

Remark 1In the deduction of(15),a usual strategy, namely linearization,is used.From this point,it looks like the traditional extended Kalmanlter(EKF).However, there still exist two signicant differences between them. (i)Because of the linearization,the related Jacobian matrices need to be computed.Comparing(15)and the EKF,it can be seen that the EKF requires to calculate the Jacobian matricesof boththe processequationandthe measurement equation,whereas only the Jacobian matrix of the measurementequation needs to be obtainedin(15),therebyreducingtheextentofthelinearization.(ii)As is wellknown, in the EKF,three variances need to be estimated,whereas (15)is not the case,resulting in the reduced computational burden.Overall,(15),whichis obtainedbymaximizingthe likelihood function,can be viewed as an extension of the EKF from the perspective of the linearization.Here,for simplicity and convenient,we vividly describe(15)as a PG.

Remark 2The resampling process,which can be regarded as an optimization problem,is to generate new particles with higher quality from the sampled particles.In this paper,we apply the framework(evolution,recombination and elimination)of the genetic algorithm(GA)to the solution of the optimization problem.Specically,the recombinationand elimination share the same idea with GA, whereas the evolution does not.In the GA-based SIR or its variants,the evolutionis generallyconductedexploiting the difference between the particles.In fact,the information available about true state that the difference carries is very limited.Only through dozens of iterations,can such methods obtain the expected performance.Different from the traditional evolution,in the proposed MSIR,the CMI instead of the difference between two particles is utilized to perform the evolution step to expect to allow a smaller number of iterations and obtain better performance.

Remark 3The main purpose of the introductionof the CMI is to correct the resampled particles and thus improve the estimation accuracy.This scheme is particularly effective when the likelihood function is sharp,in which case the CMI covers rich information on true state.However, when the measurement noise is large,the CMI becomes incredible.In this case,introducing the CMI into the resampling step may lead to degraded performance.For the reason,the proposed method is more suitable for the occasions of high-precision measurements.Fortunately,with the development of engineering technology,those occasions will become more and more.

4.Discussions

In this section,we present four discussions,involving advantages,potential problem and another alternative amelioration of the MSIR.

Discussion 1From the preceding deduction,it is known that each new particle drawn from the PG contains the CMI.Besides,another advantageof the PG is that each new particle is an unbiased estimation of the current true state,i.e.,

ProofBy substituting(11)into(2),we can obtain

Substitution of(23)into(15)yields

Discussion 2In some applications,is inreversible.To handle this problem,we use the state vector to extend the measurement vector.Hence,the modied measurement equation is dened as

where ukis a zero-mean Gaussian random disturbance with covariance matrix α2I and I is the m×m identity matrix.There are several ways to obtain the additional measurement yak.For example,the SIR itself can be used to generate the additional measurement.In this paperis calculated as follows:

After augmenting the measurement vector,a new PG is given by

Discussion 3ThePG hastheabilitytopromotetheparticles to the areas of high likelihood where the true state is most likely to exist.

ProofLetandbe the particle sets which are obtained in the(g+1)th and gth iterations,respectively.Letdenote the particle set drawn from the theoretical posterior PDF.The PDFs approximated byandare as follows:andare two differentapproximationsof p.To evaluate the quality of the approximations,the Kullback-Leibler divergence(KLD)[12,13],which measures the degree of distortion between two PDFs,is used here.The smaller the KLD,the more similar the two PDFs.The KLDs between the theoretical PDF(p)and the two approximatedPDFsandare dened as

Here,the basis of log(·)is greaterthan 1.The difference between(32)and(33)is expressed as

Inequality(35)indicates thathas a higher likelihood,i.e.

Applying(36)to(34),we obtain

Inequality(37)demonstrates thatis more similar to p andare closer to true state,thereby proving the property of the PG.

Discussion 4In the elimination,an alternative method for generating the normative particle is described as follows:

where

We denote the square of distance frombywhereis the particle with the highest value of weight.Obviously,the step-sizeranges from 0 to 1,and the farther thethe larger the step-size.

5.Simulations

In this section,the MSIR proposed in this paper was applied to two examples.One is a synthetic,scalar estimation problem which is used previously in[14–16],and the other is a range-azimuth target tracking model which is often adoptedin passive coherentlocation[17].The rootmean square error(RMSE)is used to access the estimation accuracy(EA)of all thelters.It is dened as

whereM is the numberof MonteCarlo(MC)experiments.denote the true state and correspondingestimation at time k of the mth simulation,respectively.

Example 1The DSS model for the synthetic,scalar estimation problem is written as

where γk−1is a Gamma(3,2)random variable modelling the process noise,vk∼ N(0,0.000 01).In this experiment,four differentlters(SIR,MSIR,APF,UPF)are used to implement the estimate of the state sequence xkfor k=1,...,50.The value of initial state x0is 1.In the MSIR,other parameters are set to Pa=0.9 and G=2.500 MC independent trials are conducted for all thelters for each run.

Firstly,50 particles are employed,and Fig.1 shows the comparisonof the true state with estimates of fourlters in a random simulation.Among the fourlters,the SIR and APF yield large errors at some time points such as time 17.The UPF has nearly the same performance of estimationas MSIR,whiletheMSIRperformsbetterespeciallyat time 26.

Fig.1 State estimates comparision of four flters

Fig.2 RMSE curves of different flters

Table 1 Comparision of RMSE means,RMSE stds,and average running time of the four flters with N=50,200

The computational complexity is critical to the implementof an algorithm.Amongthe SIR,APF and UPF,main factor which affects the computational complexity is the particle number N,but in the MSIR,except for N,the maximumnumber of iterations is another important factor. With the given N,the larger the G,the longer the running time of the MSIR,so a large G is not desired.Fig.3 shows the variationof runningtime of the MSIR with G.It can be known that G is linearly proportional to the computational complexity of the MSIR.To get the inuence of G on the performance of the MSIR.Fig.4 and Fig.5 compare the RMSEs and correspondingRMSE means with differentG, respectively.

Fig.3 Variation of running time of MSIR with different G

Fig.4 RMSEs comparision of MSIR with different G

Fig.5 RMSE means of MSIR with different G

On one hand,the steady-state of the MSIR is reached when G increases to 4.On the other hand,even in the case where the evolution is conducted for only one time,i.e., G=1,the EA of the MSIR is still superior to that of otherlters.This is mainly due to the fact that the particles generated from the PG make the best use of the CMI.In other words,the PG can make the predicted particles move towards domain of high likelihood quickly.Therefore,a large G is not necessary in the MSIR.

In the recombination,the recombination coefcient Pa is axed number which is predened,and different values of Pa may yield different estimation results.Next,the inuence of Pa on the EA of the MSIR is studied.In the study,50 particles are still used,but G is set as 1 for the purpose of getting rid of its inuence on the EA.Fig.6 plots the curves of the RMSE of the MSIR where Pa ranges from 0 to 1,and Fig.7 shows the correlative RMSE means.As expected,the estimation results are quite different for different Pa.Pa=0 means the RPs contain only the old particles,in which case the EA of the MSIR is the worst.On the contrary,Pa=1 means the old particles are completelyreplacedbythe new ones.The experimentalresults demonstratethat the RPs shouldbe drawnpartlyfrom the old ones,and partly from the new ones.By mixing the new and old particles,the diversity of particles is raised, resulting in the improved EA.In addition,Pa=0.8 is the optimal for this example.

Fig.6 RMSE curves of MSIR for different Pa

Fig.7 Variation of RMSE mean of MSIR for different Pa

Example 2A passive radar target tracking model is considered,whereis inreversible.The state and measurement equations for this model are described as

where

Here,xk,ykdenote the Cartesian coordinates of the target,˙xk,˙ykdenote the velocities in the x and y directions,respectively.L denotes the distance between the receiver station and transmitter station.The process noise is zero-mean Gaussian white noise,i.e.,γk−1∼ N(0,Q) where Q=diag[(2 m/s2)2(2 m/s2)2].The measurement ykconsists of two components:bistatic range and azimuth.The measurement noise vk∼N(0,R),where R=diag[(100 m)2(100 mrad)2].The initial state vector x0=[4 000 m 200 m/s 5 000 m 200 m/s]T.The SIR,APF,UPF and MSIR are applied to estimate the trajectories of the target.In this example,we set L=30 km, α=0.001,G=2,N=200.

Table 2 RMSE means,RMSE stds,and average running time of different flters when tracking a passive radar target

Fig.8 RMSEs of the estimated positions of the target using the SIR, APF,UPF and MSIR

6.Conclusions

The particle degeneracyand impoverishmentproblems are two notable shortages existed in the traditional particlelter and its variations.In this paper,a novel resampling approach,calledMSIR,is proposedtoalleviatetheproblems, where the reproduction,recombination and elimination of particlesconstitutethemainpart.Throughtheoreticalanalysis and numerical simulations,several conclusions can be drawn:(i)In the reproduction,each derivative particle drawnfromthe GP not only incorporatesthe CMI,but also is an unbiasedestimation of the currentstate,so the GP enables the particles to move towards regions of high likelihood.(ii)The recombination and elimination,as the measures of improving the diversity among the particles and valuesofweights,areeffective.By usingthem,theestimation performance is improved.(iii)The evolutional result of the MSIR is satised,and it can reach the steady-state with a small G.(iv)Augmenting the measurement vector, as an auxiliary method,is feasible in the case where the reversibility condition is not met.(v)The MSIR has better EA and stronger robustness,compared with SIR,APF and UPF.The future work can be done from the aspects of reducingthe computationalcomplexityof the MSIRand getting rid of the assumption of Gaussian measurement noise.

[1]S.Sedai,M.Bennamoum,D.Q.Huynh.A Gaussian process guided particlelter for tracking 3D human pose in video. IEEE Trans.on Image Processing,2013,22(11):4286–4300.

[2]C.Yardim,P.Gerstoft,W.S.Hodgkiss.Tracking refractivity from clutter using Kalman and particlelters.IEEE Trans.on Antennas and Propagation,2008,56(4):1060–1069.

[4]J.H.Kotecha,M.Djuric.Gaussian particleltering.IEEETrans.on Signal Processing,2003,51(10):2592–2601.

[5]J.M.Hammersley,K.W.Morton.Poor man’s Monte Carlo. Journal of the Royal Statistical Society B,1954,16(1):23–38.

[6]N.J.Gordon,D.J.Salmond,A.F.M.Smith.Novel approach to nonlinear/non-Gaussian Bayesian state estimation.IEE Proceedings F,1993,140(2):107–113.

[7]M.S.Arulampalam,S.Maskell,N.J.Gordon,et al.A tutorial on particlelters for online nonlinear/non-Gaussian Bayesian tracking.IEEE Trans.on Signal Processing,2002,50(2): 174–188.

[8]A.Doucet.On sequential Monte Carlo methods for Bayesianltering.Cambridge:Cambridge University,1998.

[9]R.Merwe,A.Doucet,N.Freitas,et al.The unscented particlelter.Technical Report CUED/F INFENG/TR 380.Cambridge:the Cambridge University,2000.

[10]M.K.Pitt,N.Shephard.Filtering via simulation:auxiliary particlelters.Journal of theAmerican Statistical Association, 1999,94(446):590–599.

[11]H.W.Li,J.Wang,H.T.Su.Improved particlelter based on differential evolution.Electronics Letters,2011,47(19): 1078–1079.

[12]T.C.Li,S.D.Sun,T.P.Sattar.Adapting sample size in particlelters through KLD-resampling.Electronics Letters,2013, 49(12):740–742.

[13]M.Chitchian,A.Simonetto,A.S.Amesfoort,et al.Distributed computation particlelters on GPU architectures for real-time control applications.IEEE Trans.on Control Systems Technology,2013,21(6):2224–2238.

[14]Y.Wang,F.C.Sun,Y.A.Zhang,et al.Central difference particlelter applied to transfer alignment for SINS on missiles.IEEE Trans.on Aerospace and Electronic Systems,2012, 48(1):375–387.

[15]J.Y.Zuo,Y.N.Jia,Y.Z.Zhang,et al.Adaptive iterated particlelter.Electronics Letters,2013,49(12):556–557.

[16]Y.H.Xi,H.Peng.MLP training in a self-organizing state space model using unscented Kalman particlelter.Journal of Systems Engineering and Electronics,2013,24(1):141–146.

[17]R.Tharmarasa,M.Subramaniam,N.Nadarajah,et al.Multitarget passive coherent location with transmitter-origin and target-altitude uncertainties.IEEE Trans.on Aerospace and Electronic Systems,2012,48(3):2530–2550.

Biographies

Yong Wu was born in 1987.He received his B.S. degree in electronics and information engineering from Nanhua University,in 2010.He is currently a Ph.D.candidate of National Lab of Radar Signal Processing in Xidian University.His research interests include particlelter,passive radar signal processing,and parallel computing.

E-mail:wuyongxidian@163.com

Jun Wang was born in 1969.He received his B.S. degree in measurement engineering,M.S.and Ph.D. degrees in signal and information processing from Xidian University,in 1990,1995 and 2000,respectively.From 1990 to 1992,he was a research assistant in Department ofMeasurement Engineering and Instrument at Xidian University.He joined National Lab of Radar Signal Processing in Xdian University in 1995,where he served as a lecturer from 1996 to 2000,an associated professor from 2000 to 2004.Since 2004,he has been a professor in National Lab of Radar Signal Processing.He is also a senior member of Chinese Institute of Electronics.His research interests include passive coherent detection and location,radar imaging,and weak signal detection.

E-mail:wangjun@xidian.edu.cn

Xiaoyong L¨u was born in 1988.He received the B.S.degree in electronics and information engineering from Zhengzhou University,in 2011.He is currently a Ph.D.candidate of National Lab of Radar Signal Processing in Xidian University.His research interests include target tracking,and passive radar signal processing.

E-mail:zzuxiaoyong@163.com

Yunhe Cao was born in 1978.He received the Ph.D. degree from Xidian University,in 2006.He is currently an associate professor at National Lab of Radar Signal Processing,Xidian University.His research interests include radar array signal processing,wideband signal processing and shadow inverse synthetic aperture radar signal processing.

E-mail:cyhxidian@gmail.com

10.1109/JSEE.2015.00051

Manuscript received January 14,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61372136).