Wei Gao,Jianguo Huang,and Jing Han

School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China

Multi-channel differencing adaptive noise cancellation with multi-kernel method

Wei Gao*,Jianguo Huang,and Jing Han

School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China

Although a various of existing techniques are able to improve the performance of detection of the weak interesting signal,how to adaptively and efciently attenuate the intricate noises especially in the case of no available reference noise signal is still the bottleneck to be overcome.According to the characteristics of sonar arrays,a multi-channel differencing method is presented to provide the prerequisite reference noise.However,the ingredient of obtained reference noise is too complicated to be used to effectively reduce the interference noise only using the classical linear cancellation methods.Hence,a novel adaptive noise cancellation method based on the multi-kernel normalized leastmean-square algorithm consisting of weighted linear and Gaussian kernel functions is proposed,which allows to simultaneously consider the cancellation of linear and nonlinear components in the reference noise.The simulation results demonstrate that the output signal-to-noise ratio(SNR)of the novel multi-kernel adaptiveltering method outperforms the conventional linear normalized least-mean-square method and the mono-kernel normalized leastmean-square method using the realistic noise data measured in the lake experiment.

adaptive noise cancellation,multi-channel differencing,multi-kernel learning,array signal processing.

1.Introduction

It is well knownthat the traditional linear adaptiveltering algorithmsincludethe least-mean-square(LMS),recursive least square(RLS),afne projection algorithm(APA)and its particular case normalized least-mean-square(NLMS). Moreover,adaptive noise cancellation(ANC)and acoustic echo cancellation(AEC)are the celebrated and successful applications of adaptiveltering methods due to the pioneer work in[1,2].The ANC model of single channel developed in[3–5]was expanded into the multi-channel or array processing to increase the signal-to-noise ratio(SNR)attracting continuous researches[6–9].Meanwhile,AEC as one of the signicant acoustic signal topics attracts considerable attention only considering the linear characteristicofechoes[10–14].With thenonlinearmethods developing,the nonlinear AEC case has been recently focused on,such as Volterralter[15–17],Bayesian approach[18,19],and kernel-based methods[20,21].

The intrinsic essence of kernel-based methods supported by the functional analysis is to map thenite low dimension input data into higher or potentially innite dimensionality reproducing kernel Hilbert spaces(RKHS), afterwards,linear processing in RKHS to solve the nonlinear problems in the original data space.Thus the single kernel-based methods are extensively studied as a powerful tool for solving the nonlinear identication problems in the last decade.On the basis of the principles of conventional linear LMS,RLS and APA adaptiveltering algorithms[2,22],the corresponding nonlinear online kernelizedadaptivelteringalgorithmsweresequentiallyproposed,including the kernel recursive least square(KRLS) [23–25],kernel least-mean-square(KLMS)[26,27],kernel afne projection algorithm(KAPA)and kernel normalized LMS(KNLMS)[28,29].An overview of monokernel adaptiveltering and its practical applications is referred to[30].As the ongoing generation of the monokernel method,multi-kernel adaptiveltering has recently becomeahotresearchtopicduetoits evenmoredegreesof freedom and features leading to better performance[31–33].Therefore,the leaky multi-kernel APA algorithm with sliding window was applied to the AEC gaining superior results in[34].In order to provide available reference noise as in the most common ANC applications,the multichannel differencing strategy based on the characteristics of sonar arrays is presented to address the problem of lacking of the reference noise.But the reference noise acquired by the multi-channel differencing method is lin-earlyandnonlinearlyrelatedwiththenoisecomponentthat needs to be reduced.Motivated by the merit of the multikernel method,the aim of this paper is to propose a novel scheme of multi-kernel adaptiveltering which consists of a linear kernel function and a Gaussian kernel function simultaneously cancelling the linear and nonlinear additive noise corrupted with the interesting signal.Increasing the SNR of the received weak signal through ANC,the proposed algorithm is of signicance to improve the detection,parameter estimation,identication and tracking for the weak signal of underwater targets.

This paper is organized as follows.In Section 2,the multi-channel differencing method is presented to acquire the necessary referenced noise employed in ANC application.In Section 3,werstly introduce the preliminary of RKHS and the single kernel nonlinear regression model, and then present the principle of adaptive noise cancellation based on the multi-kernel NLMS algorithm originating from the multi-kernel APA in detail.Section 4 shows two simulation results based on the realistic noise data measured in the practical lake experiment,which demonstrates the advantagesand effectiveness of the proposedalgorithm by the improvement of detection probability.Finally,Section 5 concludes this paper.

2.Multi-channel differencing method

The reference noise in most ANC applications is an indispensable input for suppression of the additive noise contaminating the interesting signal.Suppose that each sensor element of underwater linear arrays receives the far feild target signal from an unknown direction of arrival(DOA) corrupted by the strong noises,and the marine environment noise ignored.Since the outputs of additionalsensors (such as accelerometer)near the noise source only reect the mechanical vibration strength[5],there is no available auxiliary channel to offer the reference noise.Besides,the DOA of signals is evidently impossible to know a prior.

When the reference noise is difcult or impossible to obtain,the delayed version of the input signal is generally able to be used as the reference input.However,it must be under the conditions that the signal is narrowband and the noise is broadband,or the signal is broadband and the noise is narrowband[4].By contrast,it has been investigated and veried that the received signal by underwater sonar arrays are much more intricate than the general assumptions and conditions.The intricate underwater acousticnoisereceivedbythesonararraysincludesplatformmachine noise,screw propeller noise andow noise,which are broadband,nonstationary and spatial colored noise. Consequently,the multi-channel differencing approach is naturally developed according to the inherent feature of multi-channel of the array signal processing,namely,utilising the multiple channels degree of freedom.

Assume that there are K narrowband plane waves located at θ1,θ2,...,θK.Consider a uniform linear array (ULA)composedofM sensorswiththeinterelementspacing d that is the half wavelength of the transmitted signal.The array steering vector a(θk)∈RM×1for the kth source located at θkis dened as

where zi(n)denotes the temporal and spatial correlated noise from the homogenousnoise source,and mi(n)is the uncorrelated noise in the primary signal.In order to detect the weak target signals from all the possible DOA,the steering vector of the conventional beam scan is given by

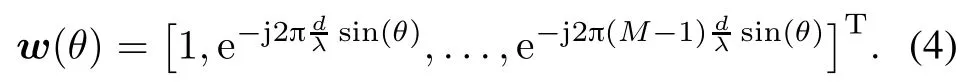
Considering using the signals received by multiple channels,the desired reference noise matrix by the multichannel differencing strategy can be modeled as

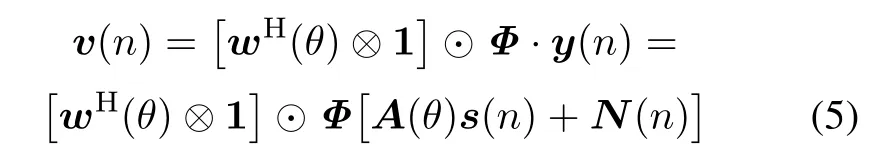
where(·)Hdenotes the transpose complex conjugate,and the operators⊗and⊙are Kronecker product and Hadmard product,respectively.The notation 1=[1,...,1]Tis an(M ×1)unit column vector,and Φ represents an (M ×M)dimensional matrix of computation of differencing for all the adjacent channels dened as

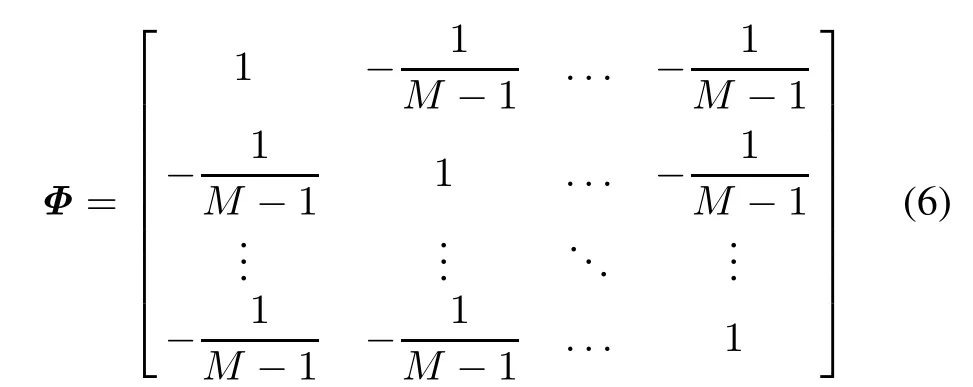
wherethetotalnumberofauxiliarychannel(M−1)canbe determined by the prior information of the received signal.Fig.1 indicates the structure of the multi-channel differencing method described as(5).Note that each entry of v(n)correspondsto the reference noise of the single channel as the input of every ANC.The reference noise input vector unfor the mth channel is dened as

Fig.1 Structure of multi-channel differencing method

Although the expression of the proposed method(5)is very compact and concise,the obtained reference noise of each channel is very complicated because of the computation involving M channels of the correlated noise.Therefore,the reference noise obtained from M channel signals has a strong nonlinear relation with the interference noise due to the effects of temporal and spatial nonlinearity of channel and motion of the platform,which is veried by the comparison of simulation results among linear and nonlinear ANC methods.On account of the linear and nonlinear components arising in the reference noise and interference noise,we will propose a novel ANC method whose core is based on the multi-kernel adaptiveltering in the next section.

3.Linear and nonlinear adaptive noise cancellation with MKNLMS

3.1Reproducing kernel Hilber spaces

Let H denote a Hilbert space of real-valued function ψ(·) on a compact subspace,and let〈·,·〉Hbe the inner product dened in the space H.Suppose that the functional evaluation Ludened by Lu[ψ]= ψ(u)is linear with respect to ψ(·)and bounded,for all u in a compact subspace U⊂Rq.By virtue of the Riesz representation,there exists a unique positive denite functionin H,denoted by κ(·,uj)and called representer evaluation, which satises[35]

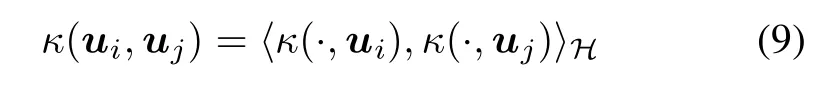
for all ui,uj∈ U.Equation(9)is the origin of the now generic term reproducing kernel to refer to κ(·,·). Denoting by ϕ(·)the map that assigns the kernel function κ(·,uj)to each input data uj,(9)immediately implies that κ(ui,uj)= 〈ϕ(ui),ϕ(uj)〉H.Thus the kernel evaluates the inner product of any pair of elements of U mapped to H without any explicit knowledge of either ϕ(·)or H.This key idea is known as the kernel trick. There are many widely used kernel functions,but we just consider the linear kernel functionand the radially Gaussian kernel function κnlin(ui,uj)= exp(−‖ui−uj‖22/2ξ)withtheGaussiankernelbandwidth ξ≥0,hereafter.

3.2Single kernel nonlinear regression

Considering the regularized kernel least-squared approach to prevent the overtting,given input vector and desired output data{(un,yn)}Nn=1⊂ U×R,the problem is to identify the ψ∗s(·)in reproducing kernel Hilber spaces (RKHS)H,namely,

where γ is a regularization nonnegative constant,and operator‖·‖His the induced norm associated with RKHS H.By virtue of the representer theorem[37,38],the optimal function ψ∗s(·)can be written as the kernel expansion in terms of measured dataIn online application,it is an intractable bottleneckthat the order of the nonlinear model N is linearly increasing with the number of sequentially measured data arrival.To overcome this barrier,thexed-size model is widely adopted as

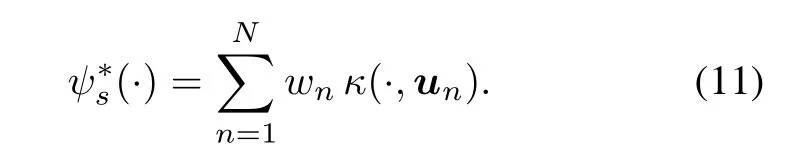
where ωlcorresponds to input vectors chosen to build the Lth order model(12)and L＜N.The set of kernel functionsis the well-known dictionary, and L is the length of the dictionary.Note that the order of the nonlinear model,that is to say the length of dictionary L,is just analogousto the orderofthe lineartransversallter in the form of mathematical expression but completely distinct in algorithm implication.

3.3MKNLMS algorithm

As a result of obtained reference noise exhibiting the high nonlinearity in virtue of the nonlinear transfer function of the adjacent channels,the classical linear ANC will consequently become invalid.Therefore,it indeed demands to extend the existing linear ANC methods into the generalized connection of linear and nonlinear cases.

Let{κk}Kk=1be the family of candidatekernelfunctions and Hkbe the RKHS dened by κk:Uk×Uk→ Rk. Consider the multidimensional mapping

with ϕk∈Hk,and〈·,·〉Mis the inner product in M as

The space M of vector-valuedfunctionsequippedwith the inner product〈·,·〉Mis a Hilbert space as(Hk,〈·,·〉Hk)is a Hilbert space for all k.We can then dene the vectorvalued representer of evaluation κM(·,u)such that

with κM(·,u)=[κ1(·,u),...,κK(·,u)]T,and operator [·,·]is the entrywise inner product.This yields the following reproducing property

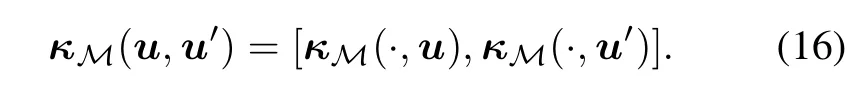
Similarly given a set of pairs of input vectors and desired output scalars{(un,yn)}Nn=1⊂U×R,we aim at estimating a multidimensionalfunctionΨ in M that minimizes the regularized least-square error

with ψk∈ Hkand yn=yn1K∈ RK,and λ is a nonnegativeregularization constant.Calculating the directional Fr´echet derivative of J(Ψ)with respect to Ψ,and equating it to zero,can yield

where wk=[w1,k,...,wN,k]Tis the kth solution of each linear system in RN:

The matrix Kkis the so-called Gram matrix with(i,j)th entry dened by κk(ui,uj),and INis the identity matrix. Finally,the optimal function ψ(u)is

Furthermore,we focus on the linear RKHS Hlinand nonlinearRKHS Hnlinover U,so the numberof candidate kernel functions is limited to K=2.From Section 3.1,it can be observed that the element κlin∈Hlinis the kernel functionκlin:U×U→R,and the element κnlin∈Hnlinis also the kernel function κnlin:U×U→ R.According to(15),consider the two dimensional weighted vectorvalued representer of evaluation κ(·,u)dened as

with κ(·,u)=[α1κlin(·,u),α2κnlin(·,u)]T,and the nonnegative weight coefcients α1+α2=1.Hence,the optimal function consisting of two different types of kernel functions is given by

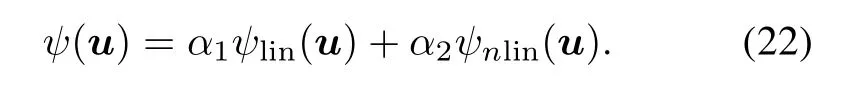
Thus,the optimum weight vector wnof(23)is given by

providedthat(HTnHn)−1exists andHnis a n-by-2Lmatrix whose ith row is given by

and the ith element of the column vector ynis yn−i+1. The afne projectionproblemat each time instant n can be presented as follows:

where if only the p most recent inputsand desired responsesare used,Hnwill reduce to the p-by-2L dimensional matrix.It can be found thatis obtained by projectingonto the intersection of recent p manifolds.Using the approach of Lagrange multiplier for the problem(26),we can get the vector of Lagrange multipliersThen the recursive update equation of the coefcients vector oflterˆwnis given by

where η is the step-size parameter and the regularization factor∈I is used to prevent the possible ill-condition of HnHTn.

In order to reduce the computational complexity and memory requirements of kernel-based methods in the online applications,the coherence sparsication criterion is chosen to generate thenite dictionary due to its simplication and efciency[28].It should be noted that the coherent criterion is readily able to be replaced with the other sparsication strategies to obtain different dictionary such as[23,33,39–41].If the candidate input κnlin(·,un)at the iteration n does not satisfy the coherence rule,the dictionary will remain unchanged.Otherwise,if the condition is met,will be inserted into the dictionary D where it is now denoted by

Let parameter p in(27)be set as 1,we immediately obtain the particular case of the multi-kernelafne projection algorithm,i.e.the MKNLMS method,whose two cases of rejection and acceptance for the input κnlin(·,un)in on online manner listed as follow:

Case 1Rejection

with

The online dictionary D remains unchanged at the instance n.

Case 2Acceptance

with

and

Then,the estimate of yncan benally written as

3.4Multi-kernel adaptive noise cancellation

The block diagram of typical adaptive noise canceller based on the weighted multi-kernellter is depicted in Fig.2.

Fig.2 Framework of multi-kernel adaptive noise cancellation

where snis the interesting signal,and the transformed noise zn=zlin,n+znlin,nfrom the auxiliary noise unpassing through the linear plus nonlinear system.The second input is the reference noise unthat is supposed to be uncorrelated with signal sn.The scheme of the multikerneladaptivenoise cancelleris that the estimate of linear and nonlinear noise is subtracted from the primary signal by identifying the reference noise.Hence,the output of ANC or the so-called error signal is given by

where the assumption that snis uncorrelated with the noises is invoked.Meanwhile,we use the hypothesis that the linear noise zlin,nis independentof the nonlinear noise znlin,n.When the proposed multi-kernel adaptivelter is exploited to adjustto minimizethe signal powerwill not be affected

It can be obviously observed that minimizing the noise poweris exactly minimizing the total output powerSince the interesting signal in the output remains constant,therefore minimizingoris equivalent to increasing the output SNR,where the outputis the best least square estimate of the signal sn.Therefore,the MKNLMS nonlinearadaptiveltering algorithm is the the hard-core of the multikernel adaptive noise cancellation.

4.Simulation results

In this section,we present two numerical simulation examples of the continuous waveform(CW)and the linear frequency modication(LFM)chirp signal to validate the effectiveness of the proposed methods by the probability of detection curves of the conventional correlation detection method compared with the linear NLMS and nonlinear single KNLMS.In contrary to that the reference noise is supposed to follow the ideal i.i.d.Gaussian distribution in[20],the noise data used in our simulation results are collected from the practical lake experiment measured by an underwater towed uniform linear sonar array with six hydrophones.The range of work frequencyof sonar arrays is from 0 kHz to 6 kHz.The waveforms of one segment of six channels underwater acoustic noise data are shown in Fig.3.And the correlation coefcients of the noise among the six hydrophones are listed in Table 1,which indicates the correlated relationship of multiple channels in the linear sonar array.

Table 1 Correlation coeffcients of six channels

Fig.3 Six channels noise data of underwater hydrophones

The stepsize η and the parameter∈are set to 0.1 and 1×10−3for all the used algorithms and two examples, respectively.The dimension of input vector q is chosen to be 5.The weighted parameters are taken as α1=0.2 and α2=0.8 for MKNLMS in two examples.The Gaussian bandwidth ξ isxed to 0.3 for KNLMS and MKNLMS algorithms.Without loss of generality,the direction of arrival(DOA)of the target is assumed to be 0°for the two examples.The lengthof inputsequenceis 3×103,afterthe processing of ANC the last 2×103samples averaged over 15 consecutive data are used as the input of correlation detection.It needstobe pointedthat theSNR is denedinthe pass band,or the input noise signal passes a band-passlter.The power spectrum density(PSD)of three used algorithmsinthespeciedSNRandtheprobabilityofdetection curves versus a range of SNR are presented to illustrate the advantagesof MKNLMS overthe general linear or nonlinear mono-kernel ANC approach.The probability of false alarm is set to 5%,and all the simulation results of detection in each SNR are individually run 100 independent Monte Carlo experiments.

4.1CW signal experiment

Fig.4 PSD and waveform of output for CW signal in SNR=–16 dB

Fig.5 Comparison of performance of NLMS,KNLMS and MKNLMS for CW signal

Thus it is completely necessary and benecial to simultaneously consider the linear and nonlinear noise adaptive cancellation when the reference noise has a complex transformation relation with the interference noise.The thresholds of coherence specication criterion μ0for both KNLMS and MKNLMS algorithms are all set to 0.95 in order to obtain two exactly same evolution curves of the length of dictionary shown in Fig.5(b)for fair comparison of performance.

4.2LFM chirp signal experiment

In orderto verifythe capabilityof the proposedmethodfor broadband signals,the target signal is supposed to be the LFM chirp signal with 1 kHz bandwidth and center frequency at 4 kHz.It is illustrated in Fig.6(d)and Fig.6(e) thatthePSD ofnonlinearadaptivenoisecancellationbased onKNLMSandMKNLMStendtobesimilarwiththePSD of LFM due to the improvement of output SNR.However, Fig.6(c)does not show the evident change compared with the PSD of the combined input signal in Fig.6(b)because of the invalidation of NLMS.Moreover,Fig.7(a)shows that MKNLMS gives even higher probability of detection in the same SNR than those of NLMS and KNLMS due to introducing the scheme of reduction of linear andnonlinearcompositionin the referencenoise,which is able to furthersuppress the total interferencenoise and increase the SNR of detection.Similarly,choosing the same threshold of coherence criterion μ0=0.95 to obtain the two overlappingevolution curves of the length of dictionary as shown in Fig.7(b),this allows us to fairly evaluate the performance of KNLMS and MKNLMS.

Fig.6 PSD and waveform of output for LFM signal in SNR=–14 dB

Fig.7 Comparison of performance of NLMS,KNLMS and MKNLMS for LFM chirp signal

5.Conclusions

In this paper,the multi-channel differencing method exploring the characteristics of sonar arrays is presented to provide the reference noise for the correlated noise cancellation.As a result of the complicated relation between the obtained reference noise and the interference noise, the multi-kernel adaptiveltering taking advantage of weighted linear and Gaussian kernel functions is proposed for the ANC of underwater sonar arrays simultaneously considering the suppression of linear and nonlinear components in interference noise.Simulation results show that the proposed algorithm has better detection ability after adaptively reducing the linear and nonlinear interference noise together,which is acquired from the lake experiment measured by the towed linear sonar array.Therefore, the proposed methods are of signicance to improve the performance of the underwater acoustic signal detection, estimation and so on.The inuence of distortion of channels and the robust ANC with multi-kernel adaptivelters should be studied and tested in the future.

[1]B.Widrow,J.R.J.Glover,J.M.McCool,et al.Adaptive noise cancelling:principles and applications.Proceedings of the IEEE,1975,63(12):1692–1716.

[2]S.Haykin.Adaptive flter theory.2nd ed.New Jersey: Prentice-Hall,1991.

[4]A.Singh.Adaptive noise cancellation.Central Elektronica Engineering Research Institute,University of Dehli,2001.

[5]J.Gorriz,J.Ramirez,S.Cruces-Alvarez,et al.A novel LMS algorithm applied to adaptive noise cancellation.IEEE Signal Processing Letters,2009,16(1):34–37.

[6]J.Meyer,C.Sydow.Noise cancelling for microphone arrays. Proc.of International Conference on Acoustics,Speech,and Signal Processing,1997,1:211–213.

[7]C.Marro,Y.Mahieux,K.Simmer.Analysis of noise reduction and dereverberation techniques based on microphone arrays with postltering.IEEE Trans.on Speech and Audio Processing,1998,6(3):240–259.

[8]H.Rogier,D.De Zutter.Prediction of noise and interference cancellation withamoving compact receiver array inanindoor environment.IEEE Trans.on Vehicular Technology,2005, 54(1):191–197.

[9]T.B.Spalt,C.R.Fuller,T.F.Brooks,et al.Abackground noise reduction technique using adaptive noise cancellation for microphone arrays.Proc.of the 17th AIAA/CEAS Aeroacoustics Conference,2011.

[10]J.Benesty,D.Morgan,M.Sondhi.A better understanding and an improved solution to the specic problems of stereophonic acoustic echo cancellation.IEEE Trans.on Speech and AudioProcessing,1998,6(2):156–165.

[11]C.Breining,P.Dreiscitel,E.Hansler,et al.Acoustic echo control–an application of very high order adaptivelters.IEEE Signal Processing Magazine,1999,16(4):42–69.

[12]J.Arenas-Garcia,A.R.Figueiras-Vidal.Adaptive combination of proportionatelters for sparse echo cancellation.IEEE Trans.on Audio,Speech,and Language Processing,2009, 17(6):1087–1098.

[13]C.Paleologu,S.Ciochina,J.Benesty.An efcient proportionateafne projection algorithm for echo cancellation.IEEE Signal Processing Letters,2010,17(2):165–168.

[14]J.Ni,F.Li.Adaptive combination of subband adaptivelters for acoustic echo cancellation.IEEETrans.onConsumer Electronics,2010,56(3):1549–1555.

[15]M.Zeller,L.Azpicueta-Ruiz,J.Arenas-Garcia,et al.Adaptive volterralters with evolutionary quadratic kernels using a combination scheme for memory control.IEEE Trans.on Signal Processing,2011,59(4):1449–1464.

[16]T.Burton,R.Goubran.A generalized proportionate subband adaptive second-order volterralterfor acoustic echo cancellation in changing environments.IEEE Trans.on Audio,Speech, and Language Processing,2011,19(8):2364–2373.

[17]L.Azpicueta-Ruiz,M.Zeller,A.Figueiras-Vidal,et al.Enhanced adaptive Volterraltering by automatic attenuation of memory regions and its application to acoustic echo cancellation.IEEE Trans.on Signal Processing,2013,61(11):2745–2750.

[18]S.Malik,G.Enzner.Recursive bayesian control of multichannel acoustic echo cancellation.IEEE Signal Processing Letters,2011,18(11):619–622.

[19]S.Malik,G.Enzner.A variational bayesian learning approach for nonlinear acoustic echo control.IEEE Trans.on Signal Processing,2013,61(23):5853–5867.

[20]H.Bao,I.M.S.Panahi.Active noise control based on kernel least-mean-square algorithm.Proc.of the 43rd IEEE international Asilomar Conference on Signals,Systems and Computers,2009:642–644.

[21]L.Azpicueta-Ruiz,M.Zeller,A.Figueiras-Vidal,et al.Adaptive combination of Volterra kernels and its application to nonlinear acoustic echo cancellation.IEEE Trans.on Audio, Speech,and Language Processing,2011,19(1):97–110.

[22]A.H.Sayed.Fundamentals of adaptive fltering.New York: John Wiley&Sons,2003.

[23]Y.Engel,S.Mannor,R.Meir.The kernel recursive least squares.IEEE Trans.on Signal Processing,2004,52(8): 2275–2285.

[24]S.Van Vaerenbergh,M.Lazaro-Gredilla,I.Santamaria.Kernel recursive least-squares tracker for time-varying regression. IEEE Trans.on Neural Networks and Learning Systems,2012, 23(8):1313–1326.

[25]B.Chen,S.Zhao,P.Zhu,et al.Quantized kernel recursive least squares algorithm.IEEE Trans.on Neural Networks and Learning Systems,2013,24(9):1484–1491.

[26]W.Liu,P.Pokharel,J.Principe.The kernel least-mean-square algorithm.IEEE Trans.on Signal Processing,2008,56(2): 543–554.

[27]B.Chen,S.Zhao,P.Zhu,et al.Quantized kernel least-meansquare algorithm.IEEE Trans.on Neural Networks and Learning Systems,2012,23(1):22–32.

[28]C.Richard,J.C.M.Bermudez,P.Honeine.Online prediction of time series data with kernels.IEEE Trans.on Signal Processing,2009,57(3):1058–1067.

[29]W.Liu,J.C.Principe.Kernel afne projection algorithms.European Association forSignal Processing Journal onAdvances in Signal Processing,2008:ID 784292.

[30]W.Liu,J.C.Principe,S.Haykin.Kernel adaptive fltering:a comprehensive introduction.New York:Jonh Wiley&Sons, 2010.

[31]M.Yukawa.Multikernel adaptiveltering.IEEE Trans.on Signal Processing,2012,60(9):4672–4682.

[32]M.Yukawa,R.I.Ishii.Online model selection and learning by multikernel adaptiveltering.Proc.of the European Signal Processing Conference,2013.

[33]F.A.Tobar,S.Y.Kung,D.P.Mandic.Multikernel least mean square algorithm.IEEE Trans.on Neural Networks and Learning Systems,2014,25(2):265–277.

[34]J.Gil-Cacho,M.Signoretto,T.van Waterschoot,et al.Nonlinear acoustic echo cancellation based on a sliding window leaky kernel afne projection algorithm.IEEE Trans.on Audio,Speech,and Language Processing,2013,21(9):1867–1878.

[35]N.Aronszajn.Theory of reproducing kernels.Transactions of the American Mathematical Society,1950,68(3):337–404.

[36]M.A.Aizerman,E.M.Braverman,L.I.Rozonoer.The method of potential functions for the problem of restoring the characteristic of a function converter from randomly observed points.Automation and Remote Control,1964,25(12):1546–1556.

[37]G.Kimeldorf,G.Wahba.Some results on Tchebychefan spline functions.Journal of Mathematical Analysis and Appllications,1971,33:82–95.

[38]B.Sch¨olkopf,R.Herbrich,R.Williamson.A generalized representer theorem,NC2-TR-2000-81.London:University of London,2000.

[39]J.Platt.A resource-allocating network for function interpolation.Neural Computation,1991,3(2):213–225.

[40]W.Liu,I.Park,J.C.Principe.An information theoretic approach of designing sparse kernel adaptivelters.IEEE Trans. on Neural Networks,2009,20(12):1950–1961.

[41]K.Slavakis,P.Bouboulis,S.Theodoridis.Online learning in reproducing kernel Hilbert spaces.P.S.R.Diniz,J.A.K. Suykens,R.Chellappa,et al.Academic press library in signal processing–signal processing theory and machine learning, London:Academic Press,2013.

Biographies

Wei Gao was born in 1983.He received his M.S. degree in signal and information processing from Northwestern Polytechinical University(NWPU), China,in 2010.He is currently pursuing his Ph.D. degree at NWPU,and simultaneously working towards to his Ph.D.degree at University of Nice Sophia-Antipolis,France.His research interests include array signal processing,adaptive noise cancellation and nonlinear adaptiveltering.

E-mail:gao wei@mail.nwpu.edu.cn

Jianguo Huang was born in 1945.He has been a professor in School of Marine Science and Technology,Northwestern Polytechinical University(NWPU),China,since 1987.He is the Chair of the IEEE Xi’an section.His general research interests include modern signal processing,array signal processing,and wireless and underwater acoustic communication theory and application.

E-mail:jghuang@nwpu.edu.cn

Jing Han was born in 1980.He received his Ph.D. degree in electronic and communication engineering from Northwestern Polytechinical University (NWPU),China,in 2008.He is currently an associate professor at School of Marine Science and Technology,NWPU.His current research focuses on underwater acoustic communications,array signal processing and statistics signal processing.

E-mail:hanj@nwpu.edu.cn

10.1109/JSEE.2015.00049

Manuscript received March 31,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61001153;61271415),the Opening Research Foundation of State Key Laboratory of Underwater Information Processing and Control (9140C231002130C23085)and the Fundamental Research Funds for the Central Universities(3102014JCQ01010;3102014ZD0041).