Feng Yang,Fei Du,Liang Liang,and Liuyi Ling

School of Management,University of Science and Technology of China,Hefei 230026,China

Full ranking procedure based on best and worst frontiers

Feng Yang*,Fei Du,Liang Liang,and Liuyi Ling

School of Management,University of Science and Technology of China,Hefei 230026,China

In the traditional data envelopment analysis(DEA) structure,the efciency score for one decision making unit(DMU) is calculated by measuring the distance of the evaluated DMU to the best practice frontier.Recent researches have provided the reasonability of considering the worst practice frontier as a supplement to the traditional DEA techniques.The existing researches take only one type of frontier into account,and they cannot compare the evaluated DMU with both the best and the worst performing DMUs.A DEA-based procedure is developed to consider the best and the worst frontiers in the same scenario where the ratio of two distances(RDS)measure is proposed.The principal application of this approach is for ranking,and,as a complement tool, for performance evaluation.The proposed approach can be used in a wide range of applications such as the performance evaluation of employees and others.Finally,a bookstore data set is used to illustrate the proposed approach.

data envelopment analysis(DEA),ranking,best frontier,worst frontier.

1.Introduction

Dataenvelopmentanalysis(DEA)isatooldesignedtoprovide a relative efciency score for each member of a group of decision making units(DMUs),which is developed by Charnes et al.(charnes,cooper and rhodes(CCR)model) [1]and extended by Banker et al.(Banker,Charnes and Cooper(BCC)model)[2].Although the DEA has been widely accepted by many researchers,it is often criticized for its inherent pitfalls or limitations.For example,Dyson et al.listed some main pitfalls in the DEA framework[3]. Accordingly,many DEA-related researches are proposed to deal with those pitfalls.

The DEA has been widely applied to rank DMUs[4–6].In the DEA framework,it seems accustomed to comparing the evaluated DMU with the best practice DMUs. Although only considering the best practice frontier is acceptable when the DEA is used as a performance evaluation tool,it is not suitable for ranking.The reasons are given below.

In the dual form of the CCR multiplier model,i.e.the CCR envelopment model(2)in Section 2.3,the evaluated DMU is compared with the combinations of all DMUs, and the distance to the DMU combinations is dened as the CCR efciency.Since the envelopment coefcients for those inefcient DMUs(the DMUs are not on the best frontier)are always zero,we can simplify the situations such that the evaluated DMU is only compared with the combinations of the efcient DMUs(the DMUs are on the best frontier).In short,in the envelopment model,the CCR efciency score is obtained by comparing the evaluated DMU with the best DMUs rather than the inefcient ones.

As discussed above,most of the traditional DEA researches only consider the best practice frontier.Actually, it is also interesting and helpful to study the worst frontier,which wasrst investigated by Jahanshahloo et al.[7] and Wang et al.[8].Jahanshahloo et al.presented an efciency measurement based on the worst frontier[7],and Wang et al.discussed the upper and lower bounds of the efciency based on the worst frontier[8].Azizi and Ajirlu investigatedtheefciencymeasurementbasedontheworstpracticeof DMUs in the presenceof non-discretionaryfactors and imprecise data[9].Chen considered the DEA efciency assessment using ideal and anti-ideal DMUs[10]. Jiang et al.considered the best and worst frontiers in the same scenario[11].Abri et al.developed the ranking rule of non-extreme efcient DMUs[12].Soltanifar and Shahghobadi provided a survey on rank preservation and rank reversal in the DEA[13].

In considering the best frontier,the evaluated DMU is measured how close it is to the best DMUs.Similarly,in considering the worst frontier,the evaluated DMU is measured how close to the worst DMUs.Because traditional DEA models based on the best frontier often face a challenge that many DMUs are determined as efcient,if we take the distances of those efcient DMUs to the worst frontier into account,we can rank those efcient DMUs easily.For example,assume that DMUs#1 and#2 are both efcient accordingto the CCR model,and DMU#1 is very far from the worst frontier while DMU#2 is very close to the worst frontier.In this example,it is surely a reasonable and acceptable strategy that ranking DMU#1 higher than DMU#2,and therefore considering the worst frontier can be treated as a complement of the traditional best-frontierbased models.

The proposed technique is mainly used to provide a fair and full ranking for all DMUs with eliminating the weightexibility effectively in a wide range of applications such as the performance evaluation of employees.Under the evaluation means based on the best frontier,an employee may be regarded as“good”if he has some advantages. Similarly,under the evaluation means based on the worst frontier,he may be also regarded as“poor”if he has some disadvantages.Our technique can equitably judge an employee by comparing his advantages and disadvantages.In addition,the proposed technique can be used as an assistant tool in the performanceevaluationas a complement of traditional DEA models.

This paper is organized as follows.In Section 2,the DEA rating methods based on the best and worst practice frontiersareintroduced.InSection3theperformancemeasurement based on the best and worst frontiers is proposed and in Section 4 the corresponding ranking techniques are proposed.In Section 5,the proposed methods are illustrated through an application of the bookstores data.In Section 6,there are some discussion and conclusions.

2.Foundations

2.1The CRS best and worst practice frontiers

Fig.1 describes the constant returns to scale(CRS)best and worst practice frontiers,where points A,B,C,D,E, F,G,H and K represent nine DMUs under evaluation.In this study,CRS assumption is attached to each DMU.We also assume that the nine DMUs have the same quantity and type of outputs.

It is known that the piecewise line REABFS is the CRS best practice frontier.Any point on Line AB is relatively efcient,and any point on Line REA or BFS(except point A and point B)is relatively weakly efcient.Similarly, we can also denote the CRS worst practice frontier by the piecewise line PECDFQ in Fig.1.Any point on Line CD is relatively inefcient,and any point on Line PEC or DFQ (except point C and point D)is relatively weakly inefcient.

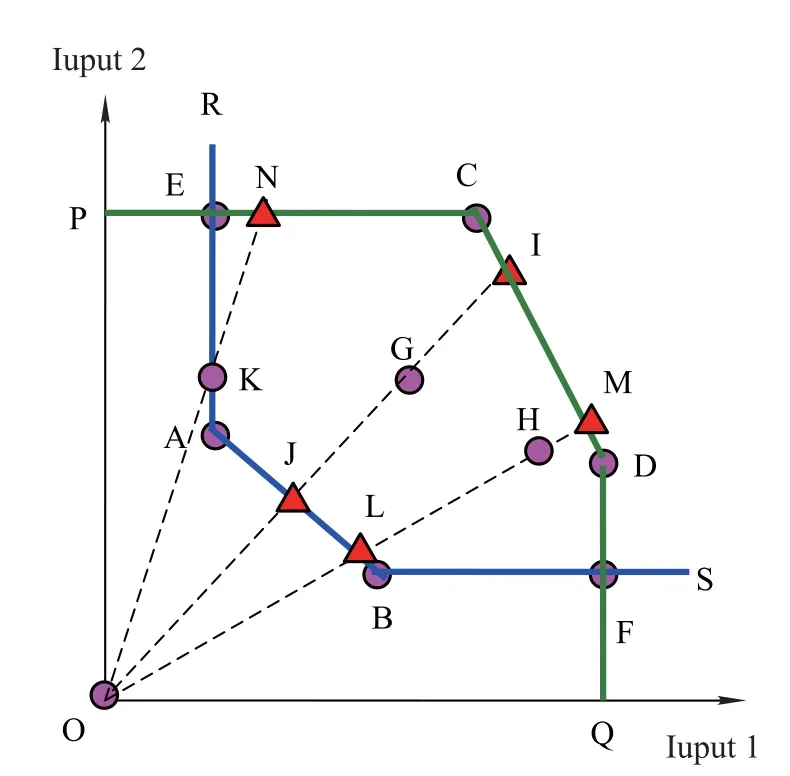
Fig.1 CRS best and worst frontiers

Since the CRS best practice frontier is known by almost every DEA researcher,we just focus on the explanation of the worst frontier.In Fig.1,all DMUs produce the same outputs.Since point C and point D are actual units,any point on Line CD represents a possible production since it can be regarded as a linear combination of point C and point D.Obviously,any point on Line CD is inefcient, because no unit is dominated by it.In other words,no unit consumes more Input 1 and more Input 2 to generate the same outputs than the units on Line CD.Thus,we can conclude that any point on CD is relatively inefcient.

Any point on Line PC,e.g.point E,consumes less Input 1 and the same Input 2 than/as point C.Although point E is better than point C,it is still inefcient,because no actual unit or no linear combination of actual units is dominated by point E,that is to say,no unit or no combination of actual units consumes both more Input 1 and more Input 2 than point E.We can conclude that any point on Line PC or Line DQ is relatively weakly inefcient.

2.2Production possibility set

In the original DEA and CCR contexts,production possi-bility set(PPS)is dened as

which is represented by the area above the piecewise Line REABFS in Fig.1.

Below we transfer our philosophy to an optimism one. From the perspective of optimism,we believe more efcient productions exist than those actual DMUs,or more efcient productions can be realized by improving techniquesorupgradingfacilities.Thus,the optimisticPPS can be denoted by

It is shown as the area PCDQO surrounded by corresponding borderlines in Fig.1.

Next we combine the two PPSs into one which represents an actual PPS.Denote

Then we have

This is the area EABFDC,and its surface is made up of the CRS best and worst practice frontiers.

2.3Effciency evaluation models

subject to

Model(1)is equivalent to the following CCR envelopment model:

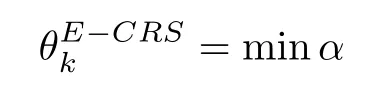
subject to:

subject to

Model(3)is equivalent to(4)

subject to

2.4Ranking based on the effciency and ineffciency scores

Some potential suggestions for the performance measurement may be the following two denitions:

Here,

However,this paper will develop another performance measurement following the logic that if one DMU is much closer to the best practice frontier and much farther from the worst practice frontier,it should have a higher efciency score.Thus we need to dene the two types of distances,one from the best practice frontier and the other from the worst practice frontier,and the ratio of these two distances is dened as a measurement to exhibit the performancefor the evaluatedDMU.In the following section, we will illustratehowtocalculatethe ratiooftwo distances (RDS)measure.

3.RDS measure for all DMUs

3.1Situation 1

Take point G in Fig.1 as an expample,its efciency score and inefciency score can be computed geometrically as follows:

Thus the RDS is

as its performance measurement based on the best and worst frontiers.

Although the performance measurement dened by(8) exhibits the ratio of the distance from the worst frontier to that from the best frontier for one DMU,it fails in the situations of the efcient and inefcient DMUs.For the efcient DMUs,their distances fromthe best frontierare zero, so the performance indicator is meaningless.For the inefcient DMUs,their distances from the worst frontier are zero,so the performance measurement is always equivalent to zero and cannot differentiate the inefcient DMUs effectively.In the following subsections we will propose an approximation substitution technique to make the definition by(8)to adapt well to the efcient and inefcient DMUs.

3.2Situation 2

Obviously,the performance of DMU¯k is very close to that of DMU k.DMU¯k is a non-efcient and noninefcient DMU,and its performance score can be computed by(8).Thus we can appraise DMU k via DMU¯k.

subject to

subject to

Therefore the performance indicator dened by(8)for DMUis shown as follows:

Then we let the performance score by(11)denote that of DMU k,since they are really close while ε is a very small positive number.

We also have the following conclusions originated from (11):

(i)The performance score for a efcient&noninefcient DMU is very large,which means that an efcient&non-inefcientDMU should be ranked higher than other types of DMUs.

3.3Situation 3

Similarly as discussed above,we can appraise an inefcient&non-efcient DMU using the approximation substitution technique by importing an adjacent DMU.

Thenwe lettheperformancescoreby(12)denotetheefciency score of DMU k,since they are really close while ε is a very small positive number.

We also have the following conclusions originated from (12):

(i)The performance score for an inefcient&nonefcient DMU is very close to zero,which means that an inefcient&non-efcient DMU should be ranked lower than all of other types of DMUs.

3.4Situation 4

4.Ranking based on RDS measure

Traditional DEA-based ranking techniques regard the efcient DMUs as of no difference.Consequently,those DMUs with the same efcient scores cannot be discriminated in ranking.Then the traditional DEA methods cannot differentiate decision making units accurately.It can be seen that the efciency measurement(RDS)we proposed can work more effectively to distinguish all DMUs and rank them than traditional ones,since they cannot distinguish all DEA efcient units,as well as those with the same DEA scores.

Another advantageof our proposedmeasurement is that we consider both the best and worst frontiers in the efciency measurement,and compare the evaluated DMU with not only the best performing units but also the worst units.Traditional DEA models only consider the distance of the evaluated DMU from the best frontier,and the corresponding efciency scores cannot reect the distance of the evaluated DMU from the worst frontier.Our efciency measurementcan reect the fair positions for the evaluated DMUsrelativetoallofotherDMUs,includingthebestand worst ones.

Accordingto the RDS scores of all DMUs,we can draw the following conclusions:

5.Numerical example

In this paper,we employ a numerical example to illustrate our approach.In the numerical example,62 bookstores are considered.Those bookstores are all private bookstoreslocated in Hefei,a city in the centre of China.In our consideration,each bookstore has two inputs,cost and labor,and one single output,i.e.,the average monthly sale.

Table 1 Effciency scores

Continued

We observethat the rankingby the efciencyscores differs greatly from the one by the inefciency scores(for almost all DMUs).This is because the different scenarios are set.In the case where only the distance from the best frontier is considered,a DMU is compared only with the best DMUs,while in the case whereonly the distance from the worst frontier is considered,a DMU is compared only with the worst DMUs.

The rightmost column in Table 1 shows the ranking from the case where the RDS is considered.In that case a DMU is compared with both the best DMUs and the worst DMUs.We can see that there are 33 DMUs whose RDS ranking orders are close to the efciency ranking orders, and 27 DMUs whose RDS ranking orders are close to the inefciency ranking orders.Thus we can conclude that the RDS rankingordersare notseparatelydependentonthe efciency ranking orders or the inefciency ranking orders.

We also see the rest 2 DMUs including#16 and#49. The RDS ranking order of#16 is the average of its efciency ranking order and inefciency ranking order.The RDS rankingorderis of#49thesameas itsefciencyranking order and inefciency ranking order.

#4 is also interesting as its RDS ranking order is much closer to the efciency ranking order and farther from the inefciency ranking order.Investigating the input and outputdataofthetwoDMUs,wendoutthattheinputdataof #4 are very special,one input is very small(the smallest of cost)andanotherinputis verylarge(the top 37%largest of labour).Therefore,it can be easily determined as efcient (rank 1 by the efciency measurement),and also easily be thoughtas inefcient(rank53 by the inefciencymeasurement).

There are many traditional ranking approaches,and we can group all DEA-based ranking approaches into six classications.Among those,the cross efciency ranking method[14,15],the super efciency ranking method [16–18]and the benchmarking ranking method[19,20] are of most inuence and acceptability.The rankings for this bookstores example according to the original super efciency approach,cross efciency approach and benchmarking approach are also presented in Table 2.

Table 2 Ranking by different models

Continued

6.Conclusions

The paper presents a DEA-based approach consideringthe best and the worst practice frontiers simultaneously.In other words,on this approach,a DMU is compared with all vital DMUs,includingthe best ones and the worst ones. Briey,a DMU is compared with all other DMUs.The previous works based on the best practice frontier are of great value and importance,however,an alternate perspective proposed by this paper is also of some acceptability.

The results from the numerical example show that the ranking originated from our model is not separately dependent to the best-frontier-based technique or the worstfrontier-based technique.The two groups of techniques have a common limitation,that is,weightexibility as discussed in the introduction.Weightexibility makes some DMUs,for instance#4,be determined as both efcient and inefcient,which may confuse the decision makers in practice.Obviously our approach can eliminate the weightexibility effectively by measuring the relative position of the evaluated unit to both frontiers.Therefore,our approach can be used in a wide range of applications such as employees performance evaluation and others.

Since the paper just gives a framework about why and how to consider the best and worst frontier simultaneously, more researches can focus on this.The further research may focus on two topics:one is to identify the importance and classication of two types of frontiers,and combine them into consideration in a more elaborate way;the other is to extendthe two frontiersto more frontiers,such as 0.9-efciency curve where the efciency scores of the DMUs on the curveare all 0.9,or 2.0-inefciencycurvewhere the inefciencyscores of the DMUs on the curve are all 2,and performanceevaluationbased on all frontierscan be made, which is really efciency relative to all other DMUs.

[1]A.Charnes,W.W.Cooper,E.Rhodes.Measuring the efciency of decision making units.European Journal of Operation Research,1978,2(6):429–444.

[2]R.D.Banker,A.Charnes,W.W.Cooper.Some models for estimating technical and scale inefciencies in data envelopment analysis.Management Science,1984,30(9):1078–1092.

[3]R.G.Dyson,R.Allen,A.S.Camanho,et al.Pitfalls and protocols in DEA.European Journal of Operational Research, 2001,132(2):245–259.

[4]F.Yang,L.Liang,G.Bi,et al.Ranking all decision making units based on their elementary difference.Journal of Systems Engineering and Electronics,2009,20(4):732–740.

[5]F.Yang,C.Yang,L.Ling,et al.A new approach to determine common weights in DEA efciency evaluation model.Journal of Systems Engineering and Electronics,2010,21(4):609–615.

[6]R.Mu,Z.Ma,C.Wei.Fuzzy data envelopment analysis approach based on sample decision making units.Journal of Systems Engineering and Electronics,2012,23(3):399–407.

[7]G.R.Jahanshahloo,M.Afzalinejad.A ranking method based on a full-inefcient frontier.Applied Mathematical Modelling, 2006,30(3):248–260.

[8]Y.M.Wang,J.B.Yang.Measuring the performances of decision-making units using interval efciencies.Journal of Computational and Applied Mathematics,2007,198(1):253–267.

[9]H.Azizi,H.G.Ajirlu.Measurement of the worst practice of decision-making units in the presence of non-discretionary factors and imprecise data.Applied Mathematical Modelling, 2011,35(9):4149–4156.

[10]J.X.Chen.A comment on DEA efciency assessment using ideal and anti-ideal decision making units.Applied Mathematics and Computation,2012,219(2):583–591.

[11]J.L.Jiang,E.P.Chew,L.H.Lee,et al.DEA based on strongly efcient and inefcient frontiers and its application on port efciency measurement.OR Spectrum,2012,34(4):943–969.

[12]A.G.Abri,G.R.Jahanshahloo,F.H.Lot,et al.A new method for ranking non-extreme efcient units in data envelopment analysis.Optimization Letters,2013,7(2):309–324.

[13]M.Soltanifar,S.Shahghobadi.Survey on rank preservation and rank reversal in data envelopment analysis.Knowledge-Based Systems,2014,60(1):10–19.

[14]T.R.Sexton,R.H.Silkman,A.J.Hogan.Data envelopment analysis:critique and extensions.R.H.Silkman.Measuring effciency:an assessment of data envelopment analysis.San Francisco,CA:Jossey-Bass,1986:73–105.

[16]P.Andersen,N.C.Petersen.A procedure for ranking efcient unitsin data envelopment analysis.Management Science, 1993,39(10):1261–1294.

[17]J.Zhu.Robustness of the efcient decision making units in data envelopment analysis.European Journal of Operational Research,1996,90(3):451–460.

[18]L.M.Seiford,J.Zhu.Infeasibility of super-efciency data envelopment analysis models.INFOR,1999,37(2):174–187.

[19]A.Charnes,C.T.Clark,W.W.Cooper,et al.A developmental study of data envelopment analysis in measuring the efciency of maintenance unitsintheUSairforces.Annals ofOperations Research,1985,2(1):95–112.

[20]A.M.Torgersen,F.R.Forsund,S.A.C Kittelsen.Slackadjusted efciency measures and ranking of efcient units. Journal of Productivity Analysis,1996,7(4):379–398.

Biographies

Yang Feng was born in 1977.He received his Ph.D.degree in management science and engineering from University of Science and Technology of China in 2006.Afterwards,he worked in Schulich School of Business York University in Canada as a visiting scholar.He returned to University of Science and Technology of China in 2007.He is a professor in School of Management,University of Science and Technology of China.He has published more than 30 articles in a wide range of international academic journals.His research interests include data envelopment analysis and multi-criteria decision modeling.

E-mail:fengyang@ustc.edu.cn

Fei Du was born in 1987.She is a Ph.D.candidate in School of Management,University of Science and Technology of China.She has published several SCI or SSCI indexed articles in international academic journals.Her research interests are data envelopment analysis and supply chain management.

E-mail:dufei@mail.ustc.edu.cn

Liang Liang was born in 1962.He received his Ph.D.degree in System Engineering from Southeast University.He is a professor in School of Management,University of Science and Technology of China.He is also the vice president of Hefei University of technology.He is also a guest editor of International Journal of Mass Customization,and Asian-Pacic Business Reviews.He was the executive Dean of School of Management University of Science and Technology of China from 2003 to 2013.He has published more than 100 articles in a wide range of international academic journals.His research interests include supply chain management and data envelopment analysis.

E-mail:lliang@ustc.edu.cn

Liuyi Ling was born in 1969.He obtained his Ph.D. degree inmanagement science and engineering from University of Science and Technology of China in 2006.He is a lecturer in School of Management, University of Science and Technology of China.He has published more than 10 articles in a wide range of international academic journals.His research interests are supply chain management and decision modeling.

E-mail:lyling@ustc.edu.cn

10.1109/JSEE.2015.00059

Manuscript received April 16,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(71121061;71271195;71322101),the National Social Science Fund of China(13CTQ042)and the USTC Foundation for Innovative Research Team(WK2040160008).