文/昌浩田 霍隆兴

二阶变系数线性微分方程的解

文/昌浩田 霍隆兴

本文给出了一类二阶线性微分方程的解法，并举例说明。

变系数；微分方程；通解

1、预备知识

考虑二阶非齐次线性微分方程[1-4]

y”+p(x)y'+q(x)y=f(x)

(1)

(其中p(x)，q(x)，f(x)是关于x的未知函数)的解；若f(x)=0，则该方程为齐次微分方程

y”+p(x)y'+q(x)y=0。

(2)

特解：若y0满足方程y”+p(x)y'+q(x)y=0，则称y0是该方程的一个特解。

通解：对于方程y”+p(x)y'+q(x)y=0，若y1(x)，y2(x)是该方程的两个线性无关的解，则称y=c1y1+c2y2(这里c1，c2为任意常数)为该方程的通解。

若知道(2)的通解为

y=c1y1(x)+c2y2(x)(这里c1，c2为常数)

通过常数变易法，设方程(1)的通解为

y=c1(x)y1(x)+c2(x)y2(x)(其中c1，c2是待定的未知函数)

由变系数二元线性方程组

解出c1'(x)，c2'(x)，再对其积分，即可求出c1(x)，c2(x)，从而可以求出方程(1)的通解。这里在知道方程(2)的一个非零特解的情况下，直接用常数变易法求方程(1)的通解。

2.主要定理及结论

若知道方程(2)的一个非零特解，则可以通过换元法化二阶方程为一阶方程，进而求出原方程的通解。

定理 若y1是方程(2)的一个非零解，则方程(1)的通解为

这里c1，c2为任意常数。

证明因为函数y1是方程(2)的特解，则

y1”+p(x)y1'+q(x)y1=0

(3)

由线性微分方程的性质知，函数cy1一定是方程(2)的解(c为任意的常数)。

设y=c(x)y1是方程(1)的解(其中c(x)是待定的未知函数)，将其求一、二阶导数并代入方程(1)，整理得:

y1c”(x)+(2y1'+p(x)y1)c'(x)+[y1”+p(x)y1'+q(x)y1]c(x)=f(x)

由式(3)，可得

这是以c(x)为未知函数的可降阶的二阶线性微分方程，解之得

则：

所以方程(1)的通解为：

例:求方程(x-1)y”-xy'+y=x(x-1)2e2x的通解。

(x-1)y”-xy'+y=0

(4)

有特解y1=ex,则设该方程的通解为y=zex，代入方程(4)，化简有

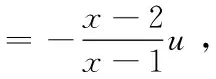
解得

积分有

故该方程的通解为

[1]罗亚平,陈仲.微分方程[M].南京:南京大学出版社,1987

[2]张学元.变系数二阶线性微分方程的一个新的可解类型[J].大学数学,2003(1):96-98.

[3]东北师范大学数学系微分方程教研室.常微分方程[M].北京:高等教育出版社,1982

[4]丁同仁，李承治.常微分方程教程[M].北京：高等教育出版社，2001：18-248.

O

A

2095-9214(2015)03-0112-01

云南大学数学系)