邓 娟，侯晋川，齐霄霏

(1. 太原理工大学 数学学院， 太原 030024；2. 山西大学 数学科学学院，太原 030006)

Banach空间上一类套代数的李环同构

邓 娟1，侯晋川1，齐霄霏2

(1. 太原理工大学 数学学院， 太原 030024；2. 山西大学 数学科学学院，太原 030006)

令N,M分别是(实或复)数域F上的Banach空间X和Y上的套,具有性质: (0)和X都是N的极限点,即 (0)+=(0),X-=X. 令AlgN和AlgM分别为相应的套代数。证明了映射Φ:AlgN→AlgM是李环同构 (即Φ是可加、李可乘的双射) 当且仅当Φ(A)=TAT-1+h(A)I对任意的A∈AlgN都成立, 或Φ(A)=-TA*T-1+h(A)I对任意的A∈AlgN都成立,其中h是在所有交换子上为零的可加泛函,T是可逆的有界线性或共轭线性算子。

Banach空间；套代数；李环同构

1 引言和主要结果

令R和S是两个环, Φ:R→S是一个映射。如果对任意的A,B∈R, Φ(AB)=Φ(A)Φ(B), 称Φ是可乘的; 如果对任意的A,B∈R, Φ([A,B])=[Φ(A), Φ(B)], 称Φ是李可乘的, 其中[A,B]=AB-BA是A和B的李积, 也叫作交换子。进而, 如果Φ是双射且李可乘的,称Φ李可乘同构;如果Φ是双射, 可加且李可乘的, 称Φ李环同构。如果R和S是数域F上的两个代数, Φ是双射,F-线性的且李可乘, 称Φ是李代数同构。对于环上的李环同构的研究, 参考[1- 3]和相关文献。在这篇文章里我们重点关注Banach空间上的套代数间的李环同构的刻画问题。

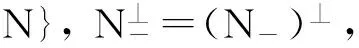
在文献[6]中, Marcoux和Sourour证明了可分复Hilbert空间上的套代数间的李代数同构都可表示为α+β的形式, 其中α是代数同构或负的代数反同构,β: AlgN→CI是在所有交换子上为零的线性映射, 即对任意的A,B∈AlgN, 满足β([A,B])=0. 要把这一结果推广到任意Banach空间上套代数的情形,其主要困难之一是Banach空间的子空间不一定是可补的。

Qi和Hou在文献[7]中通过刻画某类Banach空间套代数之间的李可乘同构推广了Marcoux和Sourour的结果。注意到, 李可乘同构不一定是可加的。令N,M分别是(实或复)数域F上的Banach空间X,Y上的套, 具有性质如果M∈M满足M-=M, 则 M在Y中可补(明显地, 如果Y是Hilbert空间或如果dimY<∞,这个假设是自然满足的)。令AlgN和AlgM分别是相应的套代数, Φ:AlgN→AlgM是双射。Qi和Hou在文献[7]中证明了:如果dimX=∞, 且存在N中的非平凡元在X中是可补的, 则Φ是李可乘同构当且仅当存在映射h:AlgN→FI, 满足对任意A,B∈AlgN,h([A,B])=0, 使得Φ(A)=TAT-1+h(A)I对任意的A∈AlgN都成立, 或Φ(A)=-TA*T-1+h(A)I对任意的A∈AlgN都成立。其中, 在第一种形式里,T:X→Y是可逆有界线性或共轭线性算子使得 N→T(N)是N到M上的序同构；而在第二种形式里,X,Y是自反的,T:X*→Y是可逆有界线性或共轭线性算子使得 N⊥→T(N⊥)是N⊥到M上的序同构。如果dimX=n<∞, 可以把套代数和上三角块矩阵代数看成一样, 则Φ是李可乘同构当且仅当存在域自同构τ:F→F, 可逆矩阵T使得要么Φ (A)=TAτT-1+h(A)对任意A都成立, 要么Φ(A)=-T(Aτ)trT-1+h(A)对任意A都成立, 其中对于矩阵A=(aij),Aτ=(τ(aij)),Atr是A的转置。特别地, 上面的结果刻画了有限维情形下的套代数之间的李环同构, 无限维情形, 套N和M满足上面所提条件的套代数之间的李环同构, 以及任何Hilbert空间上套代数之间的李环同构。

最近, Wang和Lu在文献[8]中从另外的角度推广了Marcoux和Sourour的结果, 证明了Banach空间上的任意套代数AlgN和AlgM之间的李代数同构可以表示为α+β的形式, 其中α是代数同构或负的代数反同构,β: AlgN→FI是在每个交换子上为零的线性映射。因为对于套N有非平凡的可补元的情形下, 李代数同构在文献 [9] 中已经得到刻画, Wang和Lu在文献[8] 中主要处理N中的所有的非平凡元都不可补的情形。

一个自然的问题是如何刻画任意Banach空间上套代数之间的李环同构, 从而获得比文献[8]更一般的结果。本文的目的在套的最大元及最小元都是极限元, 即(0)+=(0),X-=X的条件下, 回答上述问题。注意, 李环同构和李代数同构是非常不同的。例如套代数间的代数同构总是连续的, 然而环同构在有限维情形不一定是连续的。

下面是本文的主要结果。

定理1令N,M是(实或复)数域F上的Banach空间X和Y上的套,AlgN和AlgM分别为相应的套代数。设(0)+=(0),X-=X, 则映射Φ:AlgN→AlgM是李环同构当且仅当存在套代数间的环同构或负的环反同构Ψ, 在所有交换子上为零的可加泛函h: AlgN→F, 使得Φ(A)=Ψ(A)+h(A)I对所有A∈AlgN都成立。

定理2令N,M是(实或复)数域F上的Banach空间X和Y上的套, AlgN和AlgM分别为相应的套代数。设(0)+=(0),X-=X, 则映射Φ:AlgN→AlgM是李环同构当且仅当存在可加泛函h:AlgN→F满足对任意的A,B∈AlgN,h([A,B])=0, 且下列之一成立:

1) 存在有界可逆线性或共轭线性算子T:X→Y使得N→T(N)是N到M上的序同构, Φ(A)=TAT-1+h(A)I对任意的A∈AlgN都成立;

2)X,Y是自反的, 存在有界可逆线性或共轭线性算子T:X*→Y使得N⊥→T(N⊥)是N⊥到M上的序同构, Φ(A)=-TA*T-1+h(A)I对任意的A∈AlgN都成立。

进而, 如果F=R, 上述算子T是线性的。

注意到, 对于套N的假设条件(0)+=(0)和X-=X蕴涵X是无限维的。 本文第2部分给出预备引理, 它们中的一些也是证明主要结果中的一部分。第3部分给出主要结果定理1的证明。

2 预备引理

在这一部分, 我们给出一些预备引理, 定义和符号。它们在证明主要结果中要用到。

令X,Y是实或复数域F上的Banach空间,N,M是X和Y上的套, AlgN和AlgM分别是对应的套代数。我们知道套代数的交换子是平凡的, 即, 如果T∈B(X), 对任意算子A∈AlgN,TA=AT, 则T=λI,λ∈F。这个事实在本文中将不加解释直接应用。另外, 符号ranT, kerT和rankT分别代表算子T的值域, 零空间和秩 (即, 值域ranT的维数)。对于x∈X,f∈X*,x⊗f表示X上秩不大于1的算子, 其定义为, 对于任意向量y, (x⊗f)y=f(y)x.有时候我们用〈x,f〉表示f在x处的值f(x).

下面引理是众所周知的,它给出了套代数里一秩算子的刻画。

对于任意非平凡元E∈N, 定义

J(N,E)=

{A∈AlgN:AE=0且A*E-1=0}.

(1)

在文献[8]中, Wang和Lu证明了L是AlgN中的真极大交换李代数理想当且仅当存在唯一E∈N,L=FI+J(N,E). 下面的引理证明了任意极大交换李环理想也是这种形式。

引理2J是AlgN中的真极大交换李环理想当且仅当它是真极大交换李代数理想。

证明假设J是极大交换李环理想,则对任意A∈AlgN,C∈J和λ∈F, 我们有 [A,λC]=λ[A,C] ∈FJ, 这蕴含了FJ是李环理想。明显地,FJ也是可交换的。 因为J是极大的,因此FJ⊆J. 而J⊆FJ. 因此我们有FJ=J. 从而J也是李代数理想。反过来是明显的。 证毕。

(2)

利用上面引进的符号和类比(文献[8]中引理 4.1, 4.3, 4.4)的论证, 我们能证明下面的引理对于李环同构仍然是正确的。

是非平凡的}→

∪{J(M, F):F∈M是非平凡的}

(3)

类似于文献[8]中引理4.2, 我们有

下面的引理是显而易见的。

引理5Φ(FI)=FI.

最后, 我们给出一个引理, 它在证明我们主要结果时要用到。令E,F分别是X和X*上的子空间。 用E⊗F表示集合{x⊗f:x∈E,f∈F}. 设W,V是数域F上的线性空间,τ是F的域自同构, 如果可加映射S:W→V满足S(λx)=τ(λ)Sx对所有的x∈W,λ∈F都成立, 则称S是τ-线性的。

引理6令Xi是无限维Banach空间,i=1,2. 令Ei,Fi分别是Xi,Xi*的维数>2的闭子空间。令Ai是包含Ei⊗Fi的B(Xi)和恒等算子I的子代数。假设Ψ:A1→A2是满足 Ψ(FI)=FI和Ψ(FI+E1⊗F1)=FI+E2⊗F2的可加双射, 则存在映射γ:E1⊗F1→F, 域自同构τ:F→F使得要么

1) 对任意的x∈E1,f∈F1,Ψ(x⊗f)=γ(x,f)I+Cx⊗Df, 其中C:E1→E2,D:F1→F2都是τ-线性双射; 要么

2) 对任意的x∈E1,f∈F1,Ψ(x⊗f)=γ(x,f)I+Df⊗Cx, 其中C:E1→F2, D:F1→E2都是τ-线性双射。

引理6的证明类似文献[11]中的方法可以得到, 此处省略。

3 主要结果的证明

Φ(A((x⊗f)B)=Φ([A,[(x⊗f,B]])=

[z⊗g,[R,u⊗h]]=(z⊗g)R(u⊗h)=0.

由Φ的单射性得到A((x⊗f)B=0, 这蕴含A(x⊗f)=0或者 (x⊗f)B=0. 如果A(x⊗f)=0, 则0=Φ([A,x⊗f])=[z⊗g,R]=(z⊗g)R≠0, 矛盾; 如果 (x⊗f)B=0, 则 0=Φ([x⊗f,B])=[R,u⊗h]=R(u⊗h) ≠ 0, 矛盾。

Φ(B((x⊗f)A)=Φ([B,[x⊗f,A]])=

[u⊗h,[R,z⊗g]]=(z⊗g)R(u⊗h)=0,

下面我们给出定理1的证明。

E∈N, Φ(FI+E⊗ E⊥)=

因此, 由引理6, 存在环同构τE:F→F和映射γE: E⊗ E⊥→F使得要么

Φ(x⊗f)=γE(x,f)I+CEx⊗DE⊥f. (4)

Φ(x⊗f)=γE(x,f)I+DE⊥f⊗CEx.(5)

容易验证, 如果存在非平凡元E0∈N使得等式(4)成立, 则等式(4)对任意非平凡元 E∈N成立; 如果存在非平凡元E0∈N使得等式(5)成立, 则等式(5)对任意非平凡元E∈N成立。

假设等式(4)对非平凡的元E∈N成立。则对任意N∈N,x∈E∩N,f∈E⊥∩N, 我们有

Φ(x⊗f)=γE(x,f)I+CEx⊗DE⊥f=

γN(x,f)I+CNx⊗DN⊥f.

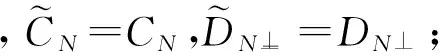
到现在为止,我们已经证明了:存在τ-线性双射C: ∪{N∈N: N≠ (0),X}→∪{M∈M: M≠ (0),Y},D: ∪{N⊥: N∈N, N≠ (0),X}→∪{M⊥: M∈M, M≠ (0),Y}以及映射 γ: ∪{E⊗ E⊥:E∈N{(0),X}}→F使得对任意x∈N,f∈N⊥, N∈N{(0),X}, 我们有

Φ(x⊗f)=γ (x,f)I+Cx⊗Df.

(6)

因此, 对任意A∈AlgN,x∈N和f∈N⊥, 由等式(6), 我们有

Φ([A,x⊗f])=[Φ(A), Φ(x⊗f)]=

Φ(A) Cx⊗Df-Cx⊗Φ(A)*Df

和 Φ([A,x⊗f])=

Φ(Ax⊗f-x⊗fA)=(γ (Ax,f)-

γ (x,A*f))I+CAx⊗Df-Cx⊗DA*f.

结合以上两个等式并且注意到I是无限秩的, 可以得到对任意N∈N{(0),X}以及x∈N,f∈N⊥, 我们有

Cx⊗Φ(A)*Df-Cx⊗DA*f=

Φ(A) Cx⊗Df-CAx⊗Df

成立。又注意到D是双射, 所以存在标量h(A)使得对任意x∈∪{N∈N: N≠ (0),X}, 有

Φ(A) Cx=CAx+h(A)Cx.

(7)

显然,h作为AlgN上的泛函是可加的。对任意A∈AlgN, 定义Ψ (A)=Φ(A)-h(A)I. 则由等式(7), 对任意A,B∈AlgN,x∈∪{N∈N: N≠ (0),X}, 我们有

Ψ(AB)Cx=CABx=

Ψ(A)CBx=Ψ(A) Ψ(B)Cx.

因为∪{N∈N: N≠ (0),X}在X中稠密且C是双射, 于是对任意A,B∈AlgN, 有Ψ(AB)=Ψ(A)Ψ(B), 也就是说, Ψ是环同构并且对任意A∈AlgN, Φ(A)=Ψ (A)+h(A)I.

类似地,如果等式(5)成立, 容易验证, 存在环反同构Ψ: AlgN→AlgM及可加泛函h: AlgN→F, 使得Φ(A)=-Ψ(A)+h(A)I对所有A∈AlgN都成立。

到此定理得证。

[1] Beidar L I, Martindale W S Ⅲ， Mikhalev A V.Lie isomorphisms in prime rings with involution[J]． J Algebra, 1994,169(1)：304-327.

[2] Bresar M. Commuting traces of biadditive mappings, commutativity preserving mappings and Lie mappings[J]． Trans Amer Math Soc, 1993,335(2)： 525-546.

[3] Martindale W S Ⅲ.Lie isomorphisms of prime rings[J]．Trans Amer Math Soc, 1969,142：437-455.

[4] Davidson K R. Nest Algebras, Pitman Research Notes in Mathematics[M]． London, New York:Longman, 1988.

[5] Longstaff W E.Operator of rank one in reflexive algebras[J]．Canad J Math, 1976(28)：19-23.

[6] Marcoux L W,Sourour A R. Lie isomorphisms of nest algebras[J]． J Func Anal, 1999,164(1)：163-180.

[7] Qi X F, Hou J C.Characterization of Lie multiplicative isomorphisms between nest algebras[J]． Sci China Math, 2011，54(11)：2453-2462.

[8] Wang T, Lu F Y.Lie isomorphisms of nest algebras on Banach space[J]． J Math Anal Appl, 2012,391(2)：582-594.

[9] Benkovic D, Eremita D. Commuting traces and commutativity preserving maps on triangular algebras[J]． J Algebra, 2004,280(2)：797-824.

[10] Hou J C, Zhang X L. Ring isomorphisms and linear or additive maps preserving zero products on nest algebras[J]. Linear Algebra and its Applications, 2004,387(1):343-360.

[11] Bai Z F, Hou J C, Du S P.Additive maps preserving rank-one operators on nest algebras[J]． Lin Multi Algebra, 2010，58(3)：269-283.

(编辑：朱倩)

LieRingIsomorphismsbetweenCertainNestAlgebrasonBanachSpaces

DENGJuan1,HOUJinchuan1，QIXiaofei2

(1.CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China；2.CollegeofMathematicalSciences,ShanxiUniversity,Taiyuan030006,China)

LetNandMbe nests on Banach spacesXandYover the (real or complex) fieldF, with the property that both (0) andXare limit points ofN, i.e., (0)+=(0) andX-=X. Let AlgNand AlgMbe the associated nest algebras, respectively. It is shown that a map Φ:AlgN→AlgMis a Lie ring isomorphism (i.e., Φ is additive, Lie multiplicative and bijective) if and only if Φ(A)=TAT-1+h(A)Ifor allA∈AlgNor Φ(A)=-TA*T-1+h(A)Ifor allA∈AlgN, wherehis an additive functional vanishing on all commutators andTis an invertible bounded linear or conjugate linear operator.

Banach spaces;nest algebras;Lie ring isomorphisms

2013-04-10

国家自然科学基金资助项目 (11171249, 11101250, 11271217)

邓娟(1986-)， 女, 湖北荆门人，硕士，主要从事算子理论与算子代数研究，(E-mail)juanhappyforever@163.com

侯晋川，博士，教授，博导，(E-mail)houjinchuan@tyut.edu.cn

1007-9432(2014)01-0133-05

O177.1

:A