于春梅

YU Chunmei

西南科技大学信息工程学院,四川 绵阳，621010

Southwest University of Science and Technology, Mianyang, 621010, Sichuan, China

引言

Nyquist采样定理表明：要精确重建信号，采样频率必须大于等于信号最高频率的两倍.由于很多信号在时域、频域或空域是稀疏的；也就是说在大多数情况下，信息存在冗余，即可以通过正交变换的方法进行压缩.那么，是否可以直接获取信号的压缩表示，而非冗余表示，使其在信息不损失的前提下，用低于Nyquist采样定理的要求对信号或者图像进行采样，同时又可以完全重构信号？这就是近年来吸引了从数学领域到信号处理、图像处理、测量、控制等各个工程领域科技人员的压缩感知问题，或压缩传感问题.该问题最核心的概念在于试图使压缩和采样同时进行，从而极大降低测量成本.

近年来美国著名学者Donoho 和Candès等根据信号的分解和逼近理论提出了压缩感知理论,为该问题提供了可能的解决方案.Candès等[1,2]从数学上证明：可以从部分傅立叶变换系数中精确重构原始信号，而Donoho[3]则以Nyquist-Shannon-Whittaker定理、Heisenberg测不准原理、Fourier投影以及优化理论为基础，提出了压缩感知的概念.Candès和Donoho证明：如果原始信号或图像的某一正交变换是稀疏的，则可以通过合适的优化算法，由少量采样值或测量值来重构信号或图像.该理论是传统信息论的延伸，使得信息理论进入了一个新的研究阶段.本文试图对稀疏求解算法做一个梳理，从最基本的优化问题到一些变形和适用范围，然后侧重对稀疏优化算法进行分类和分析，并给出最新的发展现状.

1 压缩感知的基本问题

传统的和基于压缩感知的信号采样、传输和恢复过程框架分别如图 1a和图 1b所示。

在图1b中，只需测量信号x的少量采样 y，因而无需压缩和解压缩环节.图 1b中各环节关系如下：y=Φx，其中y：M维测量信号，Φ：M*N测量矩阵,x：N维原始信号；s=Ψx，s：n维稀疏变换信号，Ψ:稀疏变换矩阵；稀疏反变换x=Ψ-1s，则y=Φx=ΦΨ-1s=Ds，s中只有k个非零元素，称为k稀疏的，D称为字典矩阵.

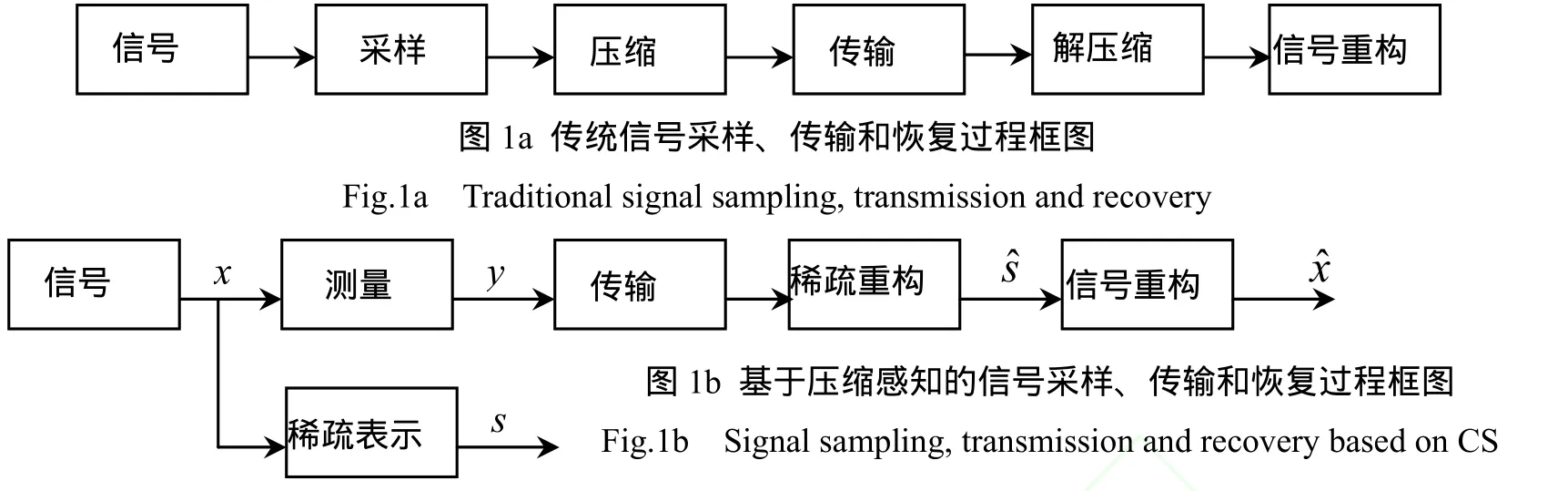
图1 信号采样、传输和恢复过程框图Fig.1 Signal sampling, transmission and recovery

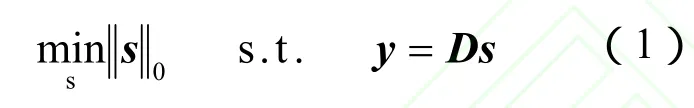
基于压缩感知的思路是：在测量矩阵Φ和稀疏变换矩阵Ψ已知的情况下，由信号的 M个测量y来重构原始N维信号x，这里的关键是：如果信号s足够稀疏，那么对于y的M个测量就可以重构N维原始信号。这个问题可以由以下的优化问题来描述：这里 l0范数指向量中非零元素的个数.求解该优化问题也即根据测量向量y求解满足测量关系（x与 y之间）和稀疏变换关系（x与s之间）的最稀疏向量s.一旦稀疏向量s求出，即可以由稀疏反变换重构原始信号x.根据以上的思路，我们可以得出压缩感知理论包含的主要内容：测量矩阵的设计；信号的稀疏表示；稀疏重构问题，即满足一定数目的测量值的条件下寻求最稀疏解的过程.

限于篇幅，本文侧重于第3个问题，即式（1）优化问题的求解，这也是压缩感知理论的核心内容.式(1)是一个典型的 NP难问题，需要穷举s中所有非零项位置的种排列的可能，这是相当困难的.Donoho和Chen[4,5,6]证明了在变换矩阵与观测矩阵不相关的条件下l0范数和l1范数的解等价，这样NP难的优化问题可以转化为l1范数最小化问题，或称之为基追踪（Basis Pursu it，BP）问题

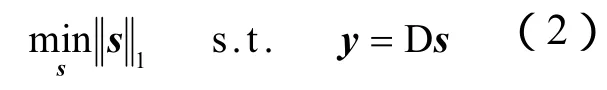
也正是基于此，l1范数优化问题成为解决稀疏求解问题的主要方法.对于对有噪声情形，该问题推广为基追踪去噪（Basis Pursuit Denoise，BPDN）问题

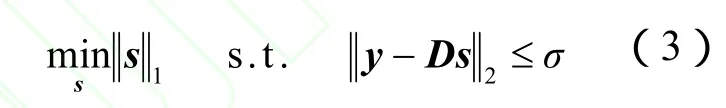
其中，σ为数据的噪声水平.或者在统计学领域的 l1范数约束下的优化问题 LASSO（Least Absolute Shrinkage and Selection Operator）[7]

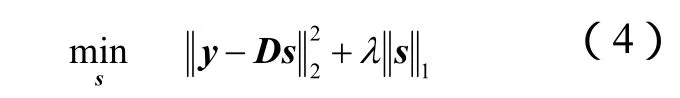
或者

实际上，（3）、（4）和（5）在适当λ、σ和q参数下是等价的[7]，不少文献并未区分二者.式（4）中l2范数项称为保真项，l1范数项称为正则项.

除了松弛为 l1范数，Gorodnitsky等[8]还提出用lp范数（0＜p＜1）代替l0范数来进行重构，非凸但结果比l1范数更稀疏.

2 与基本问题相关的稀疏优化问题

可以看出，信号重构问题即对信号的l0范数、l1范数或者 lp（0＜p＜1）范数的最小化问题.不少学者针对一些具体问题，又在上述基本优化问题的基础上，提出了适合各类不同问题的优化问题.Candes和 Tao[9]提出LASSO的稍许变化版本Dantzig selector

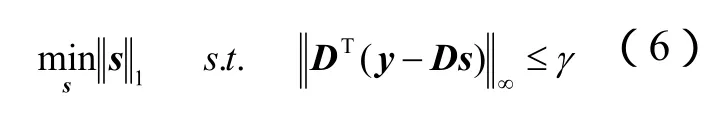
以适应变量数p远大于观测n时的情形.与LASSO不同的是，该优化模型最小化误差平方梯度向量的最大值，而不是误差的平方,其对变量选择问题特别有效.

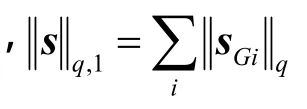
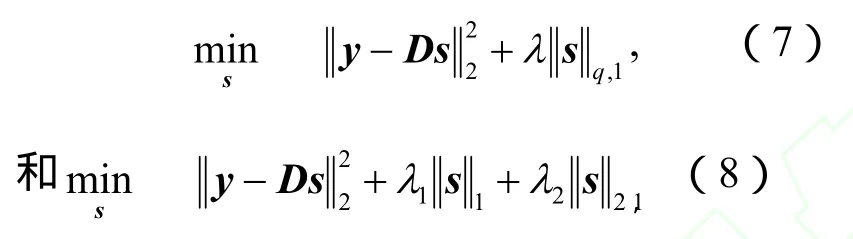
全变分（total variation, TV）模型可以看成是对一维情形的推广，其最初由Rudin等[12]提出用于图像去噪，后被推广到其他图像处理问题，该问题也通常称作ROF问题.

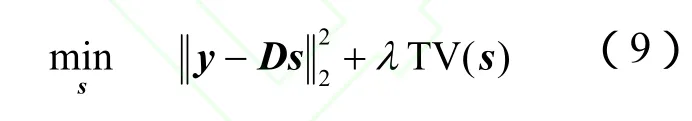
其中，TV有两种定义，一种为各向同性TV（isotropic TV）

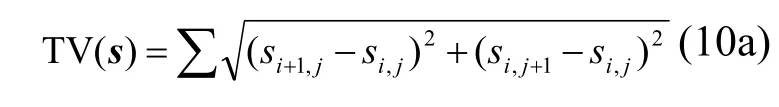
另一种为各向异性TV（anisotropic TV）

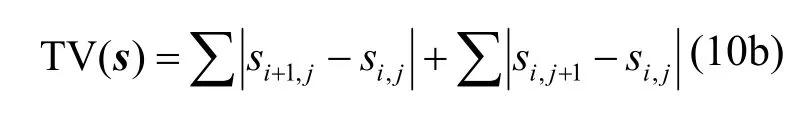
这两种模型在图像去噪的同时又能保持图像边缘，因而在图像修复、重构等方面都有良好表现.各向异性TV适合图像特征明显的区域，但对于平滑区域容易产生阶梯效应而影响效果；各向同性TV则适合图像特征不明显的区域.

以TV为基础，He等[13]提出

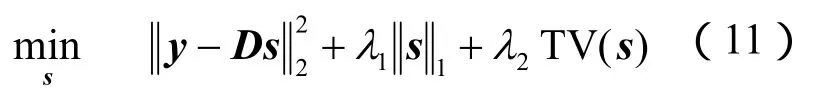
与Tibshirani等[14]提出融合LASSO（fused LASSO）

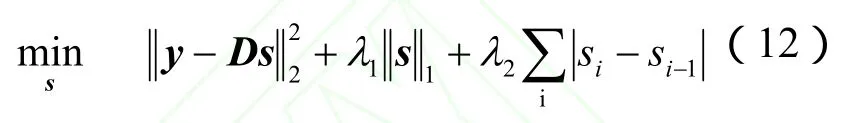
类似，使不仅系数稀疏，其差也尽量稀疏，适于特征排列有序的情形.Zou等[15]则提出弹性网（elastic net）

使强相关的预测子倾向于同时在模型中出现或消失，适用于预测子的数量比观测数量大得多的情形，并提出LARS-EN算法求解该问题.

归纳起来，稀疏优化问题如图 2所示.至于选择何种类型的优化则依赖于具体问题.对于一般的信号重构问题，基本的BPDN或者LASSO就可以；对于变量数大于观测数的情形，Dantzig selector更适合；对于图像的修复或者重构问题，全变分模型可作为首选；如果数据类型呈现组相关，采用分组 LASSO就比较适合；融合 LASSO则适合特征排列有序的情形.如果想得到比l1范数更稀疏的结果，可以将这些问题中的l1范数以 lp范数（0＜p＜1）代替.读者还可以根据问题特点设计特定的优化目标函数.

图2 稀疏优化问题Fig.2 Sparse optimization problems

3 典型的优化算法和定性比较

由于稀疏优化算法种类繁多，对其分类并非十分容易.即便如此，还是有不少作者试图对其进行总结，文献[16]将其分为l0范数下的非凸、l1范数和lp范数下的松弛；文献[17]分为最小l1范数法、匹配追踪系列算法、迭代阈值法以及专门处理二维图像问题的最小全变分法；文献[18]则将重构算法分为贪婪算法、凸优化方法和组合算法.文献[19]基追踪算法、贪婪算法和迭代阈值法.但笔者认为，这些分类有些过于笼统，有些则不够全面.本文从不同的角度，将重构算法分为活动集方法、迭代投影算子法和经典凸规划法，各方法的特点如图3所示.

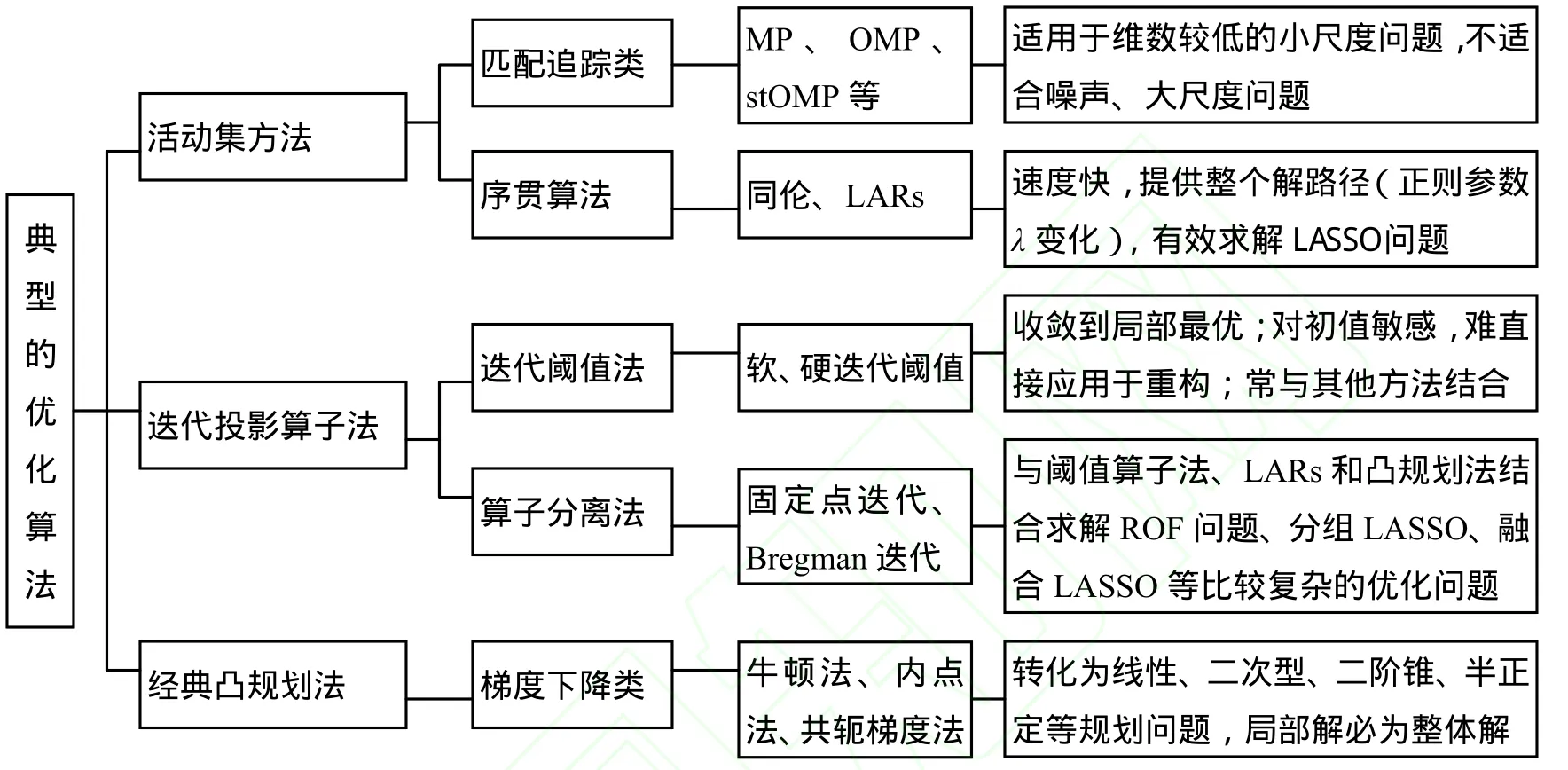
图3 典型优化算法及定性比较Figure3 Optimization algorithms and qualitative comparison

3.1 活动集方法

活动集方法是一种逐步构造最优解的方法，即逐步选择解集合，最终逼近最优解.与传统的单纯型法、内点法等从稠密解开始，迭代求最优解的方法不同，一般这类算法都是从空集开始，逐步得到稀疏解.活动集方法分为两种，一种是求解特定正则参数下的最优解，主要有贪婪算法；一种是序贯方法，有同伦算法和LARs.

贪婪算法是解决优化问题的一种基本方法，它将全局优化问题转化为逐步构造最优解的过程；在每一步都求出一个在当前阶段的最优解，而不考虑这种选择在全局看来是否最优.贪婪算法主要包括各类匹配追踪（Matching Pursuit ，MP）算法.

MP算法的基本思想是在每一次的迭代过程中，从过完备原子库里(即字典矩阵D中)选择与信号残差最为接近的原子作为匹配原子来构建稀疏逼近，经过一定次数的迭代，信号可以表示为部分原子的线性组合.由于在这些原子组成的子空间上，信号的投影并非正交，因此可能需要迭代多次算法才能收敛.针对此，文献[20]提出了正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法，该算法与MP算法采用相同的原子选择准则，不同之处在于每一步迭代中都增加了对所选原子进行正交化处理的步骤，以减少迭代次数.

MP和OMP算法在每步迭代中都要计算信号残差在字典矩阵中的每一列上的投影，计算量大，收敛速度也比较慢.Donoho等[21]于2006年提出的逐步正交匹配追踪(Stagewise Orthogonal Matching Pursuit，StOMP)算法，改善了这一状况，收敛速度有所提高.

正则化OMP(Regularized OMP,ROMP)[22]是第一个用约束等距性条件 RIP界进行分析的贪婪技术；文献[23]则每次迭代选择多列.压缩采样匹配追踪(Compressive sampling matching pursuit,CoSaMP)[24]提供了比 OMP、ROMP更全面的理论保证, 并且能在采样过程中对噪声鲁棒；除了极端稀疏的情形CoSaMP比OMP更快更有效.Dai等[25]基于回溯策略提出一个相似的算法叫子空间追踪(subspace pursuit, SP)，但该算法不是自适应于信号稀疏度的，因此其重构精度仍然不够理想.为了进一步提高重构精度,文献[26]提出了稀疏自适应匹配追踪(sparsity adaptive matching pursuit, SAMP)算法.该算法自适应于信号稀疏度，重构精度也得到了相应提高.

在这些贪婪算法中，MP、OMP、ROMP以及StOMP算法的支撑集都是在迭代过程中不断增加且不会剔除已选原子；但SP、CosaMP算法在迭代过程中为保证支撑集大小的不变必须剔除一部分原子.

序贯方法沿整个正则化路径求解，常用的有同伦（homotopy）和最小角回归（Least angle regression，LARs）.同伦是指随着λ增大，LASSO的目标函数从l2约束转为l1约束.对于LASSO问题，式（4）λ≥0或式（5）q≥0的解路径是多边形的，而且，解路径的顶点对应解子集.子集为分段常数，为λ或q的函数，仅在λ或q的关键值（对应解路径的顶点）发生变化.这个演变的子集（evolving subset）叫做有效集（active set），基于此提出的同伦算法沿着解路径从一个顶点跳到另一个顶点，开始于空的有效集在每个顶点，通过添加或移出变量来更新有效集.对于k稀疏问题，同伦算法在k步找到最优解[27].

从算法的角度讲，LARs可以看成去除了符号限制的同伦算法，不同之处在于同伦算法允许进入也允许离开有效集，这点不同使其可以严格求解全局最优问题；但这也意味着同伦算法所需的步数比LARs要多.但有证据表明，在很多情况下，同伦算法与LARs和OMP同样快[28].

LARs与OMP结构相似，区别在于OMP每一步迭代求解最小二乘问题，LARs则求解线性惩罚的最小二乘问题.事实上，LARs和同伦，在每次迭代中都采用了一种贪婪选择策略.LARs的成功除了它漂亮的几何性质之外，还有它的快速算法.

3.2 迭代投影算子法

迭代投影算子法形式上均表现为迭代求解过程，同时增加了在可行集的投影.迭代投影算子法由于计算简单，适用于高维大规模问题而深受广大学者的青睐，成为求解稀疏优化问题最有效的算法类，这其中包括阈值迭代法和各种算子分离法等.

阈值迭代法分为软阈值迭代（iterative soft-thresholding）和硬阈值迭代（iterative hard-thresholding）两种.二者均通过非线性算子进行迭代，软阈值迭代通过一个阈值参数来确定迭代中保留的项；而硬阈值迭代通过一个固定阈值进行迭代，每次迭代中保留相同数目的项.Blumensath等[29]提出了求解近似l0问题的硬阈值迭代算法.硬阈值的性能在一定条件下有很强的理论保证，但一旦某些条件不满足，则性能明显下降，甚至算法不收敛.文献[30]提出改进的硬阈值算法，保证算法的收敛性，速度更快且理论保证与原算法类似.Daubechies等[31]提出了求解l1问题的软阈值迭代算法，并给出了收敛性证明.文献[32]提出了软阈值迭代的快速算法FISTA.除此之外，软迭代阈值方法还常用于较复杂优化问题的子过程.这些复杂的问题通常可以分解为一些简单的子问题，其中的一个基本子问题LASSO可由软迭代阈值方法求解.

除了软阈值和硬阈值迭代，徐宗本团队[32-36]提出了求解l1/2问题的迭代阈值法，Half和Chalf阈值迭代算法，并将l1/2范数用于Sar图像重构，所需采样速率比l1范数低一半[37]，他们[38]还对目前已知的五大类阈值迭代算法Hard，Soft，SCAD，Half，Chalf，进行了分析比较，得出了很多有益的结论.文献[39]则结合Bregman迭代由p收缩算子求解lp范数问题，.

前向后向算子分离法（Forward backward splitting, FBS）将优化问题分解为简单子问题的迭代求解，每一次迭代分解为仅对保真项的前向(显式)步与仅对正则项的后向(隐式)步，无需求解整个目标函数的邻近算子，同时能够有效利用隐式方法的优点，从而大幅度降低计算复杂性，是凸分析中一种有效的折中方法，具有很好的收敛性[40].固定点（fixed-point）迭代和Bregman迭代均属于前后向分离算法，不同之处在于Bregman迭代用Bregman距离代替了优化目标中的正则项.

固定点迭代和线性Bregman迭代非常有效，但只能求解目标函数为l1范数+ l2范数的基本问题，对含TV的问题、含多个l1范数的问题以及其它更复杂的优化问题无法求解.针对此，不少作者使用分离算子，将Bregman迭代、接近点算子与软阈值算子结合使用，将研究不断向前推进.文献[41]用线性滤波和迭代软阈值两个简单子过程求解ROF模型对两类TV均可解；文献[42]用算子分离方法求解l1范数、l2范数、l∞范数正则以及l1/lq混合范数正则；Ma等[43]应用算子分离方法解决式（11），将优化条件分离为两部分，对其变形，并用固定点迭代fixed-point iterations算法求解[44]；文献[45]采用序贯方法加速计算过程.与原-对偶算法比较，结果差不多，但速度快3倍[46].

分离Bregman（split Bregman）算法引入新变量来实施约束并松弛，并增加关于新增变量的迭代步骤，可求解更为广泛的问题.文献[47]基于Bregman迭代提出分离Bregman迭代方法，取得了较好的效果，但没有给出收敛性证明.文献[48]将算法用于全变分优化问题，并给出了算法的收敛性分析和证明.变量分离方法与分离Bregman迭代非常相似，也引入新变量，不同之处在于用增广拉格朗日乘子来松弛目标函数.文献[49]用变量分离方法求解式（11）的优化问题，比分离Bregman迭代计算代价低，迭代次数少.文献[50]用变量分离方法，比传统的非线性共轭梯度法和分离Bregman迭代收敛快.

算子分离算法中的第二个子步需要确定稀疏性惩罚函数的邻近算子，对于大多数稀疏优化问题，软阈值迭代简单有效，在优化求解中得到了广泛应用.坐标下降法（coordinate descent）也常用来求解算子分离算法的子问题，其基本思路是一次优化一个参数（坐标），轮流循环，将复杂优化问题分解为简单的子问题，进而得出形式简单的分步迭代算法，比传统方法更易计算.该算法是迄今为止求解LASSO问题最快的算法，通常也称为FFT（Friedman + Fortran +Tricks）算法[51].

除了以上提到的算法，我们还经常看到邻近算子法、增广拉格朗日法、交错投影法等.这些算法也可以看成一类投影算子方法，他们之间在一些条件下相互联系或具有等价性[52].邻近算子为凸投影算子的推广，凸投影算子和软阈值算子均为邻近算子[53]；增广拉格朗日与线性约束的 Bregman迭代等价，又与对偶的邻近算子法联系；交错投影法与线性约束下的分离 Bregman迭代法等价，在某些条件下也与梯度投影法等价，且都可以归结为框架收缩方法[52].需要说明的是，虽然梯度投影法显然可以归于该类，但是由于习惯上将其看成传统梯度法的推广，因而本文将其归于经典的凸规划方法；而坐标下降法实际也是一种经典无约束优化方法，希望不至引起混淆.实际上从这一点也可以看出，各种方法之间存在着千丝万缕的联系，这也是导致稀疏优化算法分类困难的原因之一.

3.3 经典凸规划方法

凸优化问题是指目标函数为凸函数，约束变量取值于凸集中的优化问题.经典的用于解决该问题的方法包括内点法、牛顿法、梯度法，以及由梯度法推广而来的次梯度法和梯度投影法、次梯度投影法.内点法通过使用牛顿法求解一系列无约束优化问题来得到凸优化问题的解，在迭代的每一步中解总是可行的，因此称为内点法.一般来说，如果可以将优化问题转化为线性规划 LP、二次型规划QP、二阶锥规划SOCP或者半正定规划SDP，则很容易由这些经典的方法等求解.正是基于这样的思路，文献[54]将LASSO变形为二次规划问题，用内点法求解LASSO的对数障碍(log-barrier)形式，每一个搜索步由预调共轭梯度加速.文献[55]和[56]则化为二阶锥问题，由内点法或牛顿法求解 BPDN问题.文献[57-59]对 LASSO或BP问题用内点法在每一步的迭代中用共轭梯度 CG或最小二乘求解线性方程.文献[60]提出的用于稀疏重构的梯度追踪GPSR(Gradient Pursuit for Sparse Reconstruction)算法先将 LASSO问题转化为边界约束的二次规划问题 BCQP(bound-constrained quadratic programming)，再执行梯度投影迭代来重构图像.文献[61]采用迭代加权梯度投影算法恢复稀疏信号来求解大规模问题，速度快，且对原始信号的稀疏度不敏感.文献[62]则提出了梯度投影算法的快速分解算法.文献[63]采用子梯度寻找算法SFA来求解融合LASSO问题，并设计重启动技术来加速算法的收敛.

总之，对于稀疏优化的基本问题BPDN或者 LASSO，软阈值迭代和活动集方法应用最为广泛，而对于比较复杂的优化问题，虽然可以有其他的解决方案，但通常借助于算子分离方法简化计算，其中的子问题通常包括LASSO和可微子问题.软阈值迭代特别适合于算子分离方法的迭代过程，因而应用特别广泛.不仅如此，软阈值迭代还可以推广到求解lp范数的优化问题，因而其应用前景十分广阔.也有不少学者尝试将几种不同的方法混合使用，文献[64]在牛顿法迭代过程中用活动集策略.文献[65]先用共轭梯度法求解再用Bregman迭代优化以求解式（11）,得到较好的MR重构图像.文献[66]用同伦和坐标下降法求解BPDN问题，文献[67]采用递归自适应算法求解分组LASSO问题，结合同伦方法降低计算复杂度.

实际上，正如文献[16]所述，这些方法也可以分为直接求解 l0范数问题的贪婪追踪法、阈值法和同伦算法，以及松弛为求解l1范数和lp范数的方法.一般来说，直接求解l0范数的方法速度很快，特别在极端稀疏的情形；而对于更广泛的情形，比如信号不是特别稀疏、观测噪声较大等，凸松弛方法在处理稀疏逼近的问题上更有效.

4 总结与展望

本文将稀疏优化算法大概分成3类，实际上，这3类方法在实际应用时有时界限并不明显.或者说几种方法的综合也通常是解决较复杂问题的有效方法.如迭代法与序贯方法结合，迭代法与梯度投影法结合，分离Bregman迭代与凸规划和迭代阈值结合，内点法结合共轭梯度、预调共轭梯度，或者增广拉格朗日法结合坐标下降法等等.在稀疏优化问题上，结合最广泛的要算阈值迭代法，因为大多分离算法其中的一个迭代归结为LASSO问题，而阈值迭代法作为一种简单实用的求解算法而得到广泛应用.

随着近几年的迅猛发展，稀疏优化问题已经取得了令人瞩目的成果，但尚有一些问题亟待改进和完善，概括为以下几个方面：（1）如何设计适用于噪声情形下大尺度问题的快速优化算法.众所周知，噪声广泛存在于现实世界，抗噪性能的好坏关系到算法能否可靠应用于实际问题；而高效、快速的优化算法也是其广泛应用的前提；因而，如何设计计算复杂度较低、能有效处理大尺度问题且对噪声不敏感的优化算法是其能否有效应用于实际的关键问题.（2）如何设计适应特定应用环境的优化问题.压缩感知在信号处理尤其是图像重构领域得到了广泛的应用，但在其他具有潜在应用前景的领域如故障诊断、系统辨识以及其它与矩阵降秩相关的应用领域似乎缺乏有力的例证.作者认为这当中要解决的首要问题是对于优化目标函数的设计，使其不仅适应于具体问题、具有明确的物理含义，且能够找到普适的、全局最优的算法.（3）基于lp范数的稀疏优化理论.目前，多数优化算法是松弛为求解l1范数问题而设计的，对lp范数的优化问题研究甚少；已有的研究表明[8,37]，lp范数可以得到更加稀疏的结果，所需采样速率比l1范数低.但由于 lp范数数学性质的非凸性使得对该问题的研究一直没有突破性进展.

[1]Candés E, Romberg J, Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory, 2006,52(2):489-509

[2]Candés E.Compressive sampling.In:Proceedings of International Congress of Mathematicians. Zürich,Switzerland:European Mathematical Society Publishing House,2006.1433-1452

[3]Donoho D L.Compressed sensing.IEEE Transactions on Information Theory, 2006, 52(4):1289-1306

[4]Donoho,D.L., Huo,X.Uncertainty principles and ideal atomic decomposition.IEEE Transaction on Information Theory,2001, 47:2845-2862.

[5]Donoho,D.L., Elad,E.Maximal sparsity representation via l1minimization.In:Proceedings of the National Academy of Sciences.2003, 100:2197-2202.

[6]Chen,S., Donoho, D.L.,Saunders,M..Atomic decomposition by basis pursuit. SIAM J. on Scientific Computing,1998,20(1):33-61.

[7]Tibshirani, R..Regression shrinkage and selection via the Lasso.J.Royal Statist.Soc., B ,1996, 58 ,267-288.

[8]I.F.Gorodnitsky and B.D.Rao.Sparse signal reconstruction from limited data using focuss:A re-weighted norm minimization algorithm.IEEE Trans.On Signal Processing,1997, 45(3):600-616.

[9]Candes E, Tao T.The Dantzig selector:statistical estimation when p is much larger than n.Annals of Statistics.2007,35(6):2313–2351.

[10].Yuan M, Lin Y.Model selection and estimation in regression with grouped variables.Journal of the Royal Statistical Society, Series B.2006,68(1):49–67.

[11]Meier L, van de Geer S, Bühlman P.The group lasso for logistic regression.Journal of the Royal Statistical Society B.2008 ,70(1):53-71

[12]L.I.Rudin, S.J.Osher, and E.Fatemi, Nonlinear total variation based noise removal algorithms, Physica D, 1992,60:259-268.

[13]L.He, T.-C.Chang, S.Osher, T.Fang, P.Speier.MR image reconstruction by using the iterative refinement method and nonlinear inverse scale space methods.UCLA CAM Report 06-35, 2006.

[14]Robert Tibshirani and Michael Saunders, Saharon Rosset,, Ji Zhu and Keith Knight.Sparsity and smoothness via the fused lasso.J.R.Statist.Soc.B ,2005, 67(1):91-108

[15]Hui Zou and Trevor Hastie.Regularization and variable selection via the elastic net.J.R.Statist.Soc.B,2005, 67(2)Part 2:301–320

[16]焦李成,杨淑媛,刘芳,侯彪.压缩感知回顾与展望, 电子学报, 2011,39(7):1651-1662

[17]李树涛,魏丹.压缩传感综述.自动化学报,2009,35(11):1369-1377

[18]杨海蓉,张成,丁大为,韦穗.压缩传感理论与重构算法, 电子学报,2011,39(1):142-148

[19]戴琼海,付长军,季向阳.压缩感知研究.计算机学报,2011,34(3):425-434

[20]Tropp J, Gilbert A.Signal recovery from random measurements via orthogonal matching pursuit.Transactions on Information Theory, 2007, 53(12):4655-4666

[21]D.Donoho, Y.Tsaig, I.Drori, and J.C.Starck, Sparse solution of under determined(systems of) linear equations by stagewise orthogonal matching pursuit, IEEE Transactions on Information Theory,2012,58(2):1094-1121(2006preprint)

[22]Needell D, Vershynin R.Greedy signal recovery and uncertainty principles.In:Proceedings of the SPIE.Bellingham,WA:SPIE, 2008:68140J-12

[23]Joel A.Tropp, Stephen J.Wright.Computational Methods for Sparse Solution of Linear Inverse Problems.In:Proceedings of the IEEE, SPECIAL ISSUE ON APPLICATIONS OF SPARSE REPRESENTATION AND COMPRESSIVE SENSING, NewYork, USA:IEEE 2010,98(6):948-958

[24]Needell D, Tropp J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples.Applied and Computational Harmonic Analysis,2009, 26(3):301-321.

[25]Dai W, Milenkovic O.Subspace pursuit for compressive sensing closing the gap between performance and complexity[EB/OL].2008-01-08.http:∥ www.dsp.rice.edu/cs

[26]Thong T D, Gan L.Sparsity adaptive matching pursuit algorithm for practical compressed sensing, In:42th Asilomar Conference on Signals, Systems and Computers, Pacific Grove ,USA,2008:581-587.

[27]David L.Donoho and Yaakov Tsaig.Fast Solution of l1-norm Minimization Problems When the Solution May be Sparse.IEEE transactions on information theory ,2008, 54(11)4789-4812

[28]B.Efron, T.Hastie, I.Johnstone, and R.Tibshirani, Least angle regression, Annals of Statistics, 2004, 32(2):407-499.

[29]Blumensath T and Davies M.Iterative Hard Thresholding for Compressed Sensing.Appl.Comp.Harm.Anal,2009.,27(3):265-274

[30]Blumensath T., Davies M.E.Normalized Iterative Hard Thresholding:Guaranteed Stability and Performance.IEEE Journal of Selected Topics in Signal Processing,2010,4(2):298-309

[31]Daubechies I, Mefrise M, and Mol C.An iteative thresholding algorithm for linear inverse problems with a sparse constraint.Communication on Pure and Applied Mathematics.2004, 57(11):1413-1457.

[32]Beck, Teboulle.A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems.SIAM Journal on Imaging Sciences,2009,2(1):183-202

[33]Zongben Xu, Xiangyu Chang, Fengmin Xu and Hai Zhang.l1/2Regularization :An iterative half thresholding algorithm,Thechnical Report, 2010:No.1001.Submitted to IEEE Trans,Image Processing.

[34]Xiangyu Chang, Zongben Xu, Jinshan Zeng and Chen Xu.Modified l1/2Regularization :An iterative chalf thresholding algorithm, Thechnical Report, 2010:No.1002.Submitted to IEEE Trans, Neural Networks.

[35]Zongben Xu, Hai Zhang, Yao wang, Xiangyu Chang.l1/2regularization.Sci China Ser F, 2010, 40(3):1-11。

[36]Zongben Xu.Data Modeling:Visual Psychology Approach and l1/2Regularization Theory.In:Proceedings of the International Congress of Mathematicians Hyderabad, India,Switzerland:European Mathematical Society Publishing House ,2010

[37]Jinshan Zeng, Zongben Xu,Hai Jiang, Bingchen Zhang, Wen Hong, Yirong Wu.SAR imaging from compressed measurements based on l1/2regularization.In:IEEE International Geoscience and Remote Sensing Symposium(IGARSS), 24-29 July 2011，Vancouver, BC，pp 625 - 628

[38]常象宇, 饶过, 吴一戎, 徐宗本.如何在压缩感知中正确使用阈值迭代算法.中国科学2010,40(1)

[39] Rick Chartrand. FAST ALGORITHMS FOR NONCONVEX COMPRESSIVE SENSING:MRI RECONSTRUCTION FROM VERY FEW DATA.In:IEEE International Symposium on Biomedical Imaging(ISBI), From Nano to Macro June 28 2009-July 1 2009:262-265

[40]Combettes P L, Wajs V R.Signal recovery by proximal forward-backward splitting.Multiscale Modeling and Simulation,2006, 4(4):1168-1200

[41]Michailovich, O.V.An Iterative Shrinkage Approach to Total-Variation Image Restoration.IEEE Transactions on Image Processing, 2011,20(5):1281-1299

[42]John Duchi, Yoram Singer.Efficient Online and Batch Learning Using Forward Backward Splitting.Journal of Machine Learning Research, 2009,10():2899-2934

[43]S.Ma, W.Yin, Y.Zhang, and A.Chakraborty, An efficient algorithm for compressed MR imaging using total variation and wavelets, In:IEEE Conference on Computer Vision and Pattern Recognition, 2008, pp.1-8

[44]P.L.Lions and B.Mercier.Splitting algorithms for the sum of two nonlinear operators.SIAM Journal on Numerical Analysis,1979,16:964–979

[45]E.Hale, W.Yin, and Y.Zhang.A fixed-point continuation method for l1-regularization with application to compressed sensing. Rice University CAAM Technical Report TR07-07,2007

[46]Rick Chartrand, Brendt Wohlberg.TOTAL-VARIATION REGULARIZATION WITH BOUND CONSTRAINTS,Acoustics Speech and Signal Processing(ICASSP), In:IEEE International Conference on, Dallas, TX, 14-19 March 2010 766-769

[47]TOM GOLDSTEIN, STANLEY OSHER.THE SPLIT BREGMAN METHOD FOR L1REGULARIZED PROBLEMS.SIAM Journal on Imaging Sciences,2009,2(2):323-343.

[48]李亚峰,冯象初.L1投影问题的分裂 Bregman方法.电子学报,2010,38(11):2471-2475

[49]Xiaojing Ye, Yunmei Chen, Feng Huang.Computational Acceleration for MR Image Reconstruction in Partially Parallel Imaging. IEEE Transactions on Medical Imaging,2011,30(5):1055-1063

[50]Ramani, S.，Fessler, J.A.A Splitting-Based Iterative Algorithm for Accelerated Statistical X-Ray CT Reconstruction.IEEE Transactions on Medical Imaging,2012,31(3):677-688

[51]Friedman J, Hastie T, Hoefling H, Tibshirani R.Pathwise coordinate optimization. Annals of Applied Statistics.2007,2(1):302–332.

[52]S.Setzer.Split bregman algorithm,Douglas Rachford splitting and Frame Shrinkage,In:SSVM '09 Proceedings of the Second International Conference on Scale Space and Variational Methods in Computer Vision, Springer-Verlag Berlin,Heidelberg,2009,464-476

[53]PATRICK L.COMBETTES AND VAL´ERIE R.WAJS.SIGNAL RECOVERY BY PROXIMAL FORWARD-BACKWARD SPLITTING, Multiscale Model.Simul.2005,4(4):1168-1200

[54]Kim S, K Koh, M Lustig, S Boyd, and D Gerinvesky.A method for large-scale l1-regularized least squares problems with applications in signal processing and statistics.Tech.Report,Dept.of Electrical Engineering, Stanford University,2007 Available at www.stanford.edu/˜boyd/l1_ls.html.

[55]E.J.Candes, J.Romberg, and T.Tao.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information.IEEE Trans.Inform.Theory, 2006,52:489- 509.

[56]E.Candes, J.Romberg and T.Tao.Stable signal recovery from incomplete and inaccurate information, Communications on Pure and Applied Mathematics, 2005,59, pp.1207–1233.

[57]B.Turlach, W.N.Venables, and S.J.Wright.Simultaneous variable selection, Technometrics, 2005, 27:349-363,.

[58]C.Paige and M.A.Saunders, LSQR:An algorithm for sparse linear equations and sparse least squares, ACM Transactions on Mathematical Software, 1982,8:43–71,

[59]S.J.Wright.Primal-Dual Interior-Point Methods,Philadelphia, PA,USA:SIAM Publications, 1997.

[60]M.Figueiredo, R.Nowak, and S.J.Wright, Gradient Projection for Sparse Reconstruction:Application to Compressed Sensing and Other Inverse Problems.IEEE Journal of Selected Topics in Signal Processing, 2007,1(4):586-597.

[61]Jun Deng, Guanghui Ren, Yansheng Jin and Wenjing Ning.Iterative Weighted Gradient Projection for Sparse Reconstruction. Information Technology Journal,2011,10(7):1409-1414

[62]Dan Wei, Shutao Li, Mingkui Tan, Fast Decomposed Gradient Projection Algorithm for Sparse Representation,JDCTA:International Journal of Digital Content Technology and its Applications, 2012, 6(2):76-84

[63]Jun Liu, Lei Yuan, Jieping Ye.An Efficient Algorithm for a Class of Fused Lasso Problems.In:KDD’10, July 25-28, 2010,Washington, DC, USA.

[64]Benedetta Morini, Margherita Porcelli, Raymond H.Chan.A reduced Newton method for constrained linear least-squares problems.Journal of Computational and Applied Mathematics,2010,233(9):2200-2212

[65]T C.Chang, L.He, T.Fang.MR Image Reconstruction from Sparse Radial Samples Using Bregman Iteration, Proc.Intl.Soc.Mag.Reson.Med.2006,14():696

[66]Chunshan Liu，Zakharov, Y.V，Teyan Chen.Broadband Underwater Localization of Multiple Sources Using Basis Pursuit De-Noising.IEEE Transactions on Signal Processing,2012,60(4):1708-1717

[67]Chen Y.，Hero A.Recursive l1,∞Group lasso.IEEE Transactions on Signal Processing,2012(preprint)