王小斌,张宇功,范学良

(兰州交通大学 数理与软件工程学院，甘肃 兰州 730070)

混沌是非线性系统所独有且广泛存在的一种非周期运动形式,它作为动力学的一个分支，广泛地存在于多个科学领域.近年来，随着计算机技术等的迅速发展，关于非线性系统混沌学的研究引起了大量学者的关注[1-13].当前混沌理论研究主要从以下几个方面展开：产生混沌的机理和途径；混沌的判据和统计特性；奇怪吸引子和吸引域的几何结构；各类系统中混沌现象的深入研究；混沌的控制和工程应用.

在非线性科学中，混沌现象指的是一种确定的但不可预测的运动状态，它是非线性动力系统的固有特性，是非线性系统普遍存在的现象.常见的典型混沌系统有：Lorenz系统，Rossler系统[4]，Chua电路[6]，Duffing振子[11]，Logistic系统，Henon映射[10]等等.本文以上田振子系统为模型，通过对其进行理论和非线性动力学行为等的分析，运用数值仿真验证了混沌的特性,并用反馈线性化方法控制了该系统的混沌，将其控制到稳定的周期轨道，利用数值模拟验证了它的有效性.

1 上田振子系统的动力学分析

1.1 上田振子系统模型及其混沌吸引子

考虑如下形式的上田振子系统：

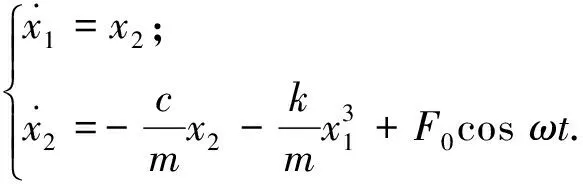
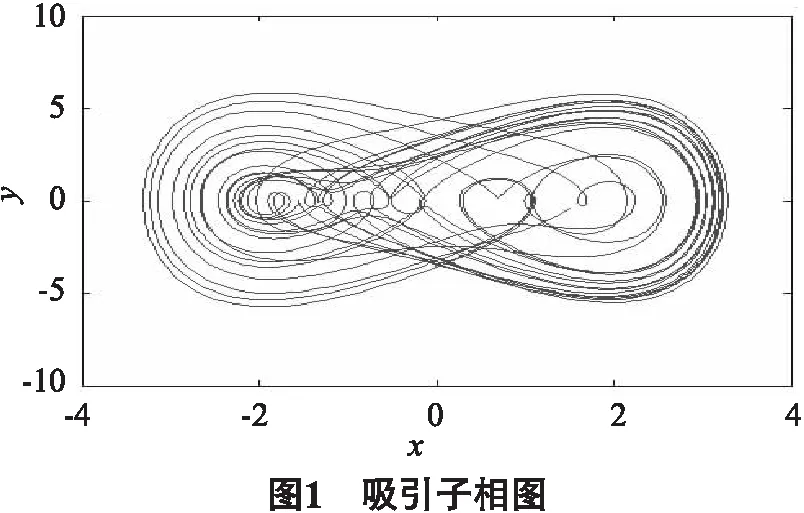
选取一组参数：m=1,k=1,ω=1,c=0.05,当F0=7.5时，取系统初值为(10，10)，利用Matlab求得该系统的2个Lyapunov指数为：λ1=0.13,λ2=-0.14.说明系统在该组参数下进入了混沌状态.这组参数下的混沌吸引子相图如图1.

从图1可以明显地看到，混沌吸引子具有极其复杂的图像，其运动也是极不稳定的，且具有复杂的折叠和拉伸轨线，吸引性很强.

由于该系统是耗散系统，故而我们接下来考虑它的散度：

1.2 Poincare截面图及其时间响应图

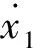
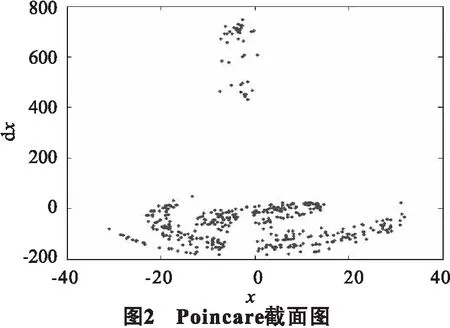
显然，从图2可以看到，截面上所呈现的是一些成片的具有分形结构的密集点，因此，毫无疑问，此时系统的运动就是混沌. 系统混沌运动的时间响应具有非周期性，解的流对初始条件非常敏感，这是混沌运动的典型特征. 在该组参数下系统的时间响应图如图3所示.

1.3 分岔图及其Lyapunov指数图

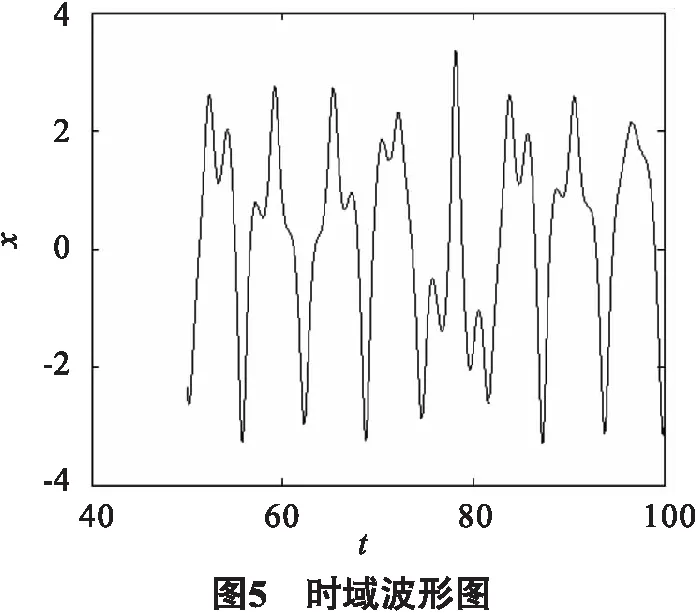
Lyapunov指数反映的是初值状态的敏感性，它所表示的数学特征为相空间中邻近轨迹的平均指数发散率. 若系统的参数发生改变，则系统平衡点处的稳定性必定发生改变，从而导致系统的运动状态的变化，利用系统的分岔图和Lyapunov指数图可以直观明了地观察系统参数变化时系统的运动状态的变化情况. 因此，分岔图和Lyapunov指数图是研究系统动力学的一种最有力且必不可少的工具. 图4为在该组参数下时间趋于无穷时系统的Lyapunov指数图，图5为其时域波形图，它反映了随时间的变化系统相应运动的变化.图6给出了系统随参数F变化时的分岔图，图7为随参数F变化的Lyapunov指数图.图8、9分别为系统在参数c变化时的分岔图和Lyapunov指数图。从这些图我们可以看到：当Lyapunov指数大于0时，必将产生混沌区域.当Lyapunov指数从正值到0再到负值时，系统发生切分岔现象.当Lyapunov指数由负值到0再到负值时，则发生倍周期分岔. 当其从负值到0再到正值时，此时系统恰好从周期运动过度到混沌运动. 由图4～9可知该系统的动力学行为特点.

2 控制上田振子系统中的混沌

下面将这一理论运用于上田振子系统

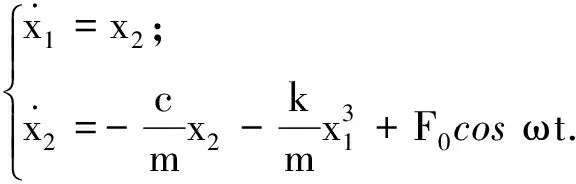
式中m,c和k分别为系统的参数，F0和ω分别为外加周期激励信号的振幅和频率，x为系统t时刻的状态. 并且当m=1,k=1,ω=1,c=0.05时，系统处于混沌状态.

下面对系统施加控制，输入控制信号u，相应系统变形为：

其对应的矢量场f和g(其中f，g为定义域D⊂Rn上的光滑向量场)分别为：

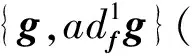
z1=x1；

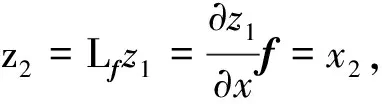
由于该系统是2阶的，由文献[4]可得相应输入变换：

通过以上变换，可得

3 仿真分析

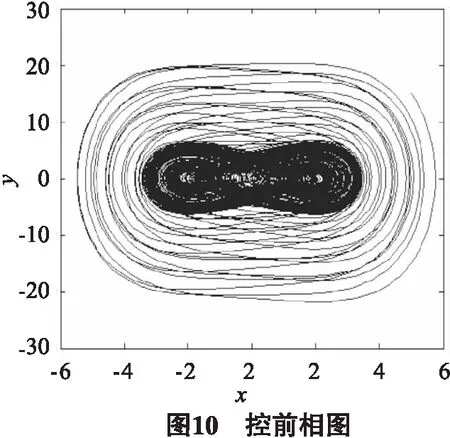
为了验证上述反馈线性化控制方法的可行性，以不稳定平衡点x=(0,0)为例，假设外部输入v=-6z1-8z2，取初值为(-1,0.5)，对系统的混沌进行控制，图10和11为上田振子系统控制前后的相图，由仿真结果可知，通过反馈线性化方法将上田振子混沌系统控制到了不稳定平衡点(0,0).

当参数m=1,k=1,ω=1,c=0.05,F0=7.5时，上田振子系统处于混沌状态，接着选择反馈控制器q1=0,q2=px1. 分别加到上田振子系统的2个方程上，得到受控系统为：

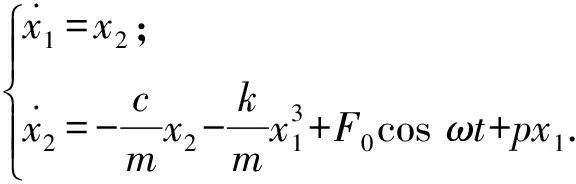
图12、13是受控系统的反馈增益系数p关于x的分岔图及其对应的Lyapunov指数图.

由图12、13可知，当取反馈增益p=1.0时，系统由混沌状态变为周期解. 与图1相比，受控系统的相平面如图14所示.

仿真结果表明设计的控制器可以将这一混沌系统控制到稳定的周期轨道.

4 结语

通过Poincare截面图、时间响应图、随系统单个参数变化的分岔图和Lyapunov指数图对上田振子系统的动力学特性进行了分析，得到了该系统参数在某一区间内的运动状态，最后通过非线性系统的反馈线性化方法，将混动系统化为线性系统，成功地控制了该混沌系统，并将其控制到一个不稳定平衡点(0,0). 接着又通过设计线性反馈控制器，进一步将混沌控制到稳定的周期轨道，仿真结果验证了它们的有效性.

参考文献:

[1] 吴祥兴，陈忠.混沌学导论[M].上海：上海科学技术文献出版社，1997.

[2] LI T Y, YORKE J A. Period three implies chaos[J]. The American Mathematical Monthly, 1975, 82(10): 985-992.

[3] PYRAGAS K. Continuous control of chaos by self-controlling feedback[J]. Physics Letters A, 1992, 170(6): 421-428.

[4] 韩萍，基于反馈线性化的Rosler混沌系统控制[J],渤海大学学报:自然科学版，2011,32(2):120-123.

[5] 陆同兴.非线性物理概论[M].北京:中国科技大学出版社,2002:1-67

[6] CHUA L O, YANG L. Cellular neural networks: Applications[J]. Circuits and Systems, IEEE Transactions on, 1988, 35(10): 1273-1290.

[7] ISIDORI A. Nonliner control system [M]. 3 ed. New York:Springer,1995.

[8] 刘向东，黄文虎，混沌系统延迟反馈控制的理论与实验研究[J].力学进展，2001,31(1)：18-31.

[9] LORENZ E N. 混沌的本质[M]. 刘式达,译.北京：气象出版社，1997.

[10] 刘晓君,常迎香,李险峰.Henon系统的混沌控制研究[J]. 齐齐哈尔大学学报：自然科学版，2006，22(3):23-26.

[11] 尹小舟.基于反馈线性化方法的同步[J].连云港职业技术学院学报:自然科学版,2008,21(3): 110-116.

[12] 郝柏林.从抛物线谈起——混沌动力学引论[M]. 上海：上海科技教育出版社，1993.

[13] 陈关荣.动力系统的混沌化[M]. 上海：上海交通大学出版社，2006.

[14] OTT E, GREBOGI C, YORKE J A. Controlling chaos[J]. Physical Review Letters, 1990, 64(11): 1196.

[15] 邹艳丽,罗晓曙,方锦清.用比例微分控制器实现混沌控制[J].广西师范大学学报:自然科学版，2002，20(3):9-13．