张 雷

(无锡工艺职业技术学院 基础部，江苏 宜兴 214206)

近年来，具有阶段结构的种群动力学模型已引起了许多学者的关注，并取得了大量的研究成果[1-5]，在种群生态学研究中具有非常重要的理论意义和应用价值.但这些研究都是在捕食与被捕食是绝对关系假设下提出的，而在自然环境中，存在大量的捕食与被捕食是相对的情况，即成年捕食者捕食被捕食者，但幼年捕食者不具备捕食能力，其有可能成为此系统中被捕食者的捕食对象，对此类捕食系统研究的文献相对较少，通过对此类系统的研究可以给种群的保护提供依据，促进生态可持续发展及生物种群的多样性.因此，本文讨论如下具有阶段结构的修正捕食系统

(1)

其中x(t)表示食饵种群密度，y1(t),y2(t)分别表示t时刻幼年、成年捕食者的种群密度，a1(t)表示食饵种群的内禀增长率，a2(t),a3(t)分别表示幼年、成年捕食者的死亡率，bi(t)(i=1,2,3)分别表示种群密度制约因素，c1(t)表示食饵种群对幼年捕食者的捕食转化率，c2(t)表示食饵种群对幼年捕食者的捕食率，d1(t)表示成年捕食者对食饵的捕食率，d2(t)表示成年捕食者对食饵的捕食转化率，β1(t)表示成年捕食者的生育率，β2(t)表示捕食者幼年到成年的转化率. 假设该系统中的各项系数均为严格正的ω-周期函数.本文主要通过利用重合度理论中的延拓定理讨论系统的正ω周期解的存在性.

1 引理

1)对任意λ∈(0,1),Ly=λNy的任意解满足y∉∂Ω∩DomL；

2)对任意y∈∂Ω∩KerL,QNy≠0且deg{JQN,Ω∩KerL,0}≠0.

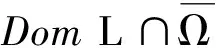
2 主要结论

假设

定理1 若ri>0(i=1,2,3,4,5)，则系统(1)至少存在1个正ω周期解.

证明对系统(1)作变换x(t)=exp{u(t)},yi(t)=exp{vi(t)},i=1,2，则有

(2)

取X=Z={y(t)=(u(t),v1(t),v2(t))T∈C(R,R3)|y(t+ω)=y(t)}，记

则X,Z在范数||·||下是Banach空间.令

则L为有界线性算子，且

KerL={(u(t),v1(t),v2(t))T∈X|(u(t),v1(t),v2(t))T∈R3}，

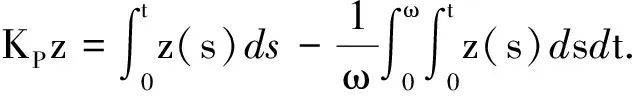
于是

和

考虑算子方程Ly=λNy,λ∈(0,1),y∈X,即

(3)

将(3)式从0到ω积分并整理得

(4)

(5)

(6)

由(3)～(6)式，有

(7)

(8)

(9)

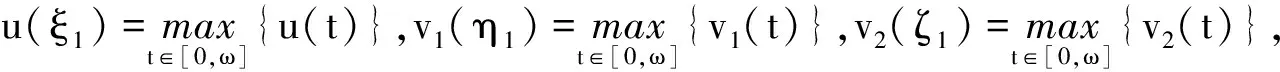
a1(ξ1)+c1(ξ1)ev1(ξ1)=b1(ξ1)eu(ξ1)+d1(ξ1)ev2(ξ1)，

(10)

β1(η1)ev2(η1)-v1(η1)=a2(η1)+b2(η1)ev1(η1)+c2(η1)eu(η1)，

(11)

β2(ζ1)ev1(ζ1)-v2(ζ1)+d2(ζ1)eu(ζ1)=a3(ζ1)+b3(ζ1)ev2(ζ1).

(12)

由(10)式得

(13)

1)当v1(η1)≥v2(ζ1)时，由(11)式可得

即

(14)

从而

(15)

所以

(16)

由(13)和(14)式可得

即

(17)

2)当v1(η1)

(18)

由(13)和(18)式可得

(19)

故

(20)

由(13)和(20)式可得

(21)

由1)和2)可知

u(ξ1)

(22)

由(7)、(8)、(9)和(22)得

(23)

(24)

(25)

a1(ξ2)+c1(ξ2)ev1(ξ2)=b1(ξ2)eu(ξ2)+d1(ξ2)ev2(ξ2)，

(26)

β1(η2)ev2(η2)-v1(η2)=a2(η2)+b2(η2)ev1(η2)+c2(η2)eu(η2)，

(27)

β2(ζ2)ev1(ζ2)-v2(ζ2)+d2(ζ2)eu(ζ2)=a3(ζ2)+b3(ζ2)ev2(ζ2).

(28)

3)当v1(η2)≥v2(ζ2)时，由(28)式可得

即

(29)

从而

(30)

由(22) 、(26)和(30)式可得

即

(31)

4)当v1(η2)

即

(32)

从而

(33)

由(22) 、(26)和(32)式可得

即

(34)

由(29)～(34)式可知，记

则

u(ξ2)>u1，v1(η2)>u2，v2(ζ2)>u2.

(35)

由(22)、(23)和(35)得

由(22)、(24)和(35)得

由(22)、(25)和(35)得

令U1=max{|M1|,|m1|}，U2=max{|M2|,|m2|}，U3=max{|M3|,|m3|}，则

|u(t)|

显然Ui(i=1,2,3)的选取与λ无关，令U=U1+U2+U3+C且C取得足够大，使得

从而，对任意λ∈(0,1),算子方程Ly=λNy的任意解满足y∉∂Ω.

下面考虑代数方程

对于参数μ∈[0,1]，容易验证方程的解(u,v1,v2)T也满足

|u|

(36)

由(36)，对于任意的y∈∂Ω∩KerL，都有QNy≠0.由于lmQ和KerL同构，取同构映射J:lmQ→KerL，J(c)=c.构造如下同伦映射：

G(μ,y)=μJQNy+(1-μ)H(y)，μ∈[0,1]，

且

再由(36)，对任意的y∈∂Ω∩KerL和μ∈[0,1]，都有G(μ,y)≠0，且H(y)=0有唯一解.根据同伦不变性有

deg{JQN,Ω∩KerL,0}=deg{H,Ω∩KerL,0}≠0.

参考文献:

[1] 陈丹,张耘嘉,张树文.具有巢寄生行为和阶段结构的两种群模型分析[J].纯粹数学与应用数学,2010,26(4) :656-662.

[2] 张艳波,王万雄.具有阶段结构且食饵有避难所的模型分析[J].数学的实践与认识,2011,41(8)：238-242.

[3] LIANG Gui-zhen,LI Kun.Dynamics of a non-autonomous predator-prey model with stage structure and delays [J] . 数学杂志,2011,31(3):415-422.

[4] 高巧琴,雒志江.具有阶段结构和功能反应混合模型的持久性和周期解[J].生物数学学报,2008,23(3):443-448.

[5] CAI Li-ming,FANG Qin-hua,SONG Xin-yu.Permanence and stability in a predator-prey system with stage structure and delays[J].应用数学,2006,19(3):484-491.

[6] GAINES R E, MAWHIN J. Coincidence degree and nonlinear differential equations[M]. Berlin: Springer-Verlag, 1977:40-45.

[7] 刘敏，陈斯养.具有收获和分段常数变量的捕食-被捕食模型的分支分析[J].云南师范大学学报：自然科学版，2013，33(5)：41-47.