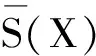关于两类右分配的强双幺半群的自由对象
2014-03-26田径孙晓青李江华
田径,孙晓青,李江华
(西安理工大学 理学院,陕西 西安 710048)
1 引言与预备知识
近年来,随着理论计算机科学的发展和实际应用的需要,关于强双幺半群的研究受到理论计算机学者和代数学者的重视。作为一类比环[1]和半环更为一般的代数系统,强双幺半群不必满足乘法对加法的分配律,因此也被称为伪半环。

设(S,+,·,0,1)是一个(2,2,0,0)-型代数。如果(S,+,0)和(S,·,1)都是幺半群,则称(S,+,·,0,1)为双幺半群。进一步,若对任意a,b∈S都有a+b=b+a和a·0=0·a=0·0=0成立,则称(S,+,·,0,1)为强双幺半群[4]。称强双幺半群S是加法幂等的,如果对任意的a∈S,总有a+a=a成立。此外,称一个强双幺半群S是右[左]分配的,如果对任意的a,b,c∈S,总有等式(a+b)·c=a·c+b·c[c·(a+b)=c·a+c·b]成立。通常的半环就是满足左、右分配律的强双幺半群。
例1:
1) 代数(N∞,+,min,0,∞)是强双幺半群[5],其中N∞=N∪{∞},+和min是自然数集N上通常的加法和取极小元运算并满足对任意的a∈N∞,有:
a+∞=∞+a=∞
min{a,∞}=min{∞,a}=a
若n为正整数,则有:
min{n,n+n}=n≠n+n=min{n,n}+min{n,n}
故分配律不成立。
2) 代数([0,1],⊕,·,0,1)是强双幺半群[8],其中·是通常实数的乘法,利用通常实数的加法和减法定义二元运算⊕定义为:

3) 设(C,+,0)是一个交换的幺半群。CC是集合C到其自身映射的全体。对任意的f,g∈CC,令f+g仍为定义在C上的映射使得(f+g)(c)=f(c)+g(c)对所有c∈C成立。再定义恒等映射和常元映射I1和I0,为:
那么代数(CC,+,∘,I0,I1)是只满足右分配律的强双幺半群,这里对任意的f,g∈CC和c∈C,有(f∘g)(c)=f(g(c))。
显然,由全体加法幂等的右分配的强双幺半群形成的代数类是一个簇[9],记为RS。本文研究RS的两个子簇LRS和URS分别满足附加恒等式y+xy≈y和y+xy≈xy。第2节利用后缀码的代数性质,构造两个(2,2,0,0)-型代数并证明它们分别属于LRS和URS。进一步将在第3节证明这两个代数分别是LRS和URS的自由对象。
2 后缀码
设X为非空字符集,称为字母表。称X中有限多个字符形成的字符串为X上的字。特别地称不含任何字符的字为空字,记为ε。称由若干字形成的集合(有限或无限)为形式语言(或语言)。进一步,记X*为X上字的全体。对任意的x,y∈X*,记xy为字x和y的并置,即:xy=x1x2…xny1y2…ym,其中,x=x1x2…xn,y=y1y2…ym,n,m为正整数,则xy∈X*。易见, 并置是X*上的二元运算。在并置运算的意义下,X*成为一个幺半群,称为由X生成的自由幺半群 。并称X+=X*{ε}为由X生成的自由半群[10]。
定义X*上的二元关系≤,为:
容易验证,≤是X*上的偏序关系。设A⊆X+是一个非空语言。若A中任意两个不同的字在偏序关系≤下都无法比较,则称A为X上的后缀码[11]。记X上有限后缀码的全体为S(X)。显然,A为后缀码当且仅当下列蕴含式成立:

例2 设X={a,b}并且A={a,ba,bb},B={aa,bb,ab}。A不是后缀码B是后缀码。
文献[10]详细阐述了后缀码的组合性质与代数性质。并证明如果A和B都是后缀码,则A∘B也是后缀码,这里∘是通常语言的乘法运算,定义为:
(∀X,Y⊆X*)X∘Y={xy∈X*|x∈X,y∈Y}.
由于运算∘是结合的,所以(S(X),∘)是半群。
给定非空集A⊆X+。令L(A)[U(A)]为A在偏序关系≤下极小元[极大元]的全体,即:
L(A)={x∈A|(∀y∈A)y≤x⟹y=x}
U(A)={x∈A|(∀y∈A)x≤y⟹y=x}
由后缀码的定义容易证明性质1。
性质 1:设非空集A⊆X+,那么以下两个结论成立:
①L(A)和U(A)都是后缀码;
②A为后缀码当且仅当L(A)=U(A)=A。
根据性质1,在S(X)上定义两个二元运算+和⊕,即:
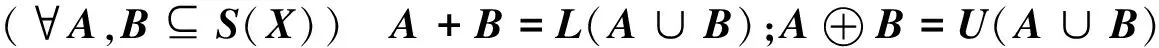
这样就得到了两个(2,2)-型代数(S(X),+,∘)和(S(X),⊕,∘)。
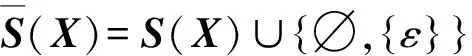
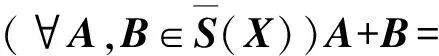
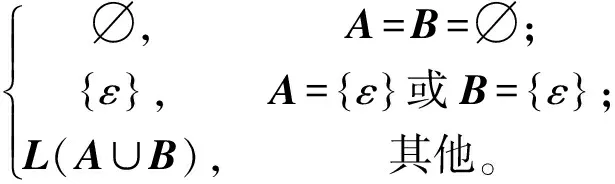

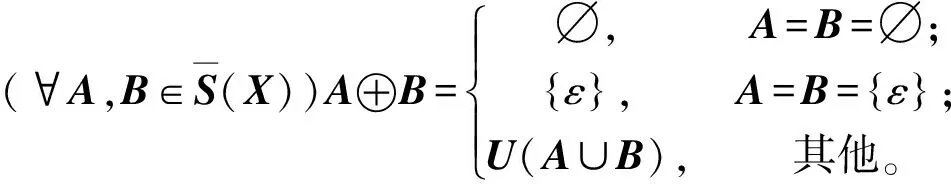

进一步,有:

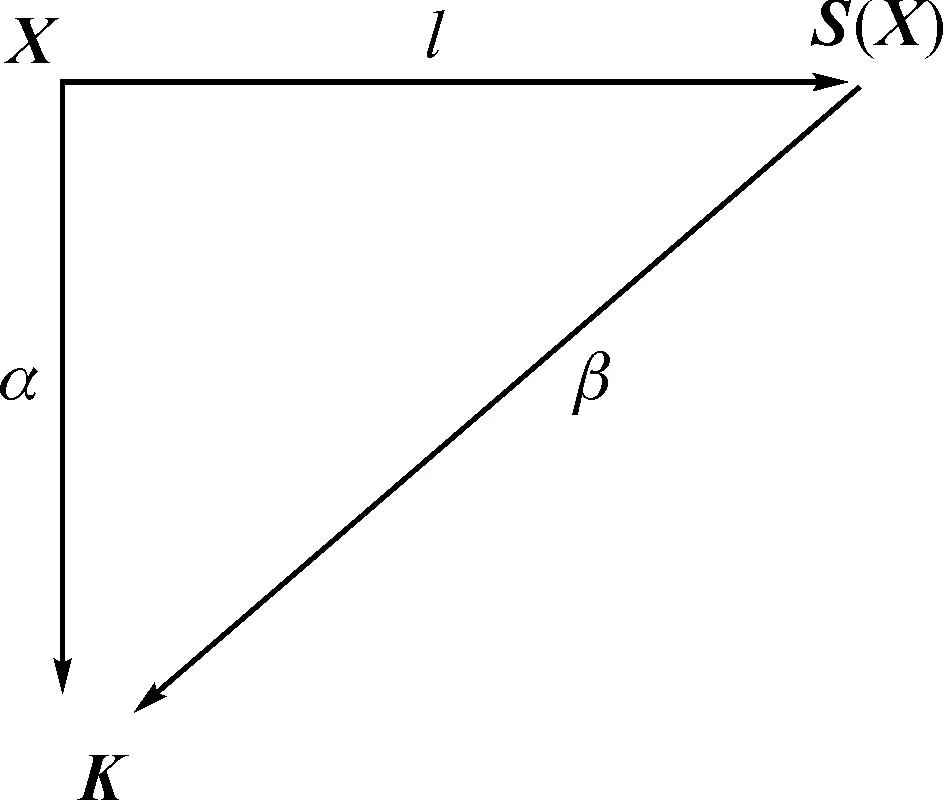
假设xy≤uv,其中,x∈A∪B,y∈C。则存在z∈X*,使得uv=zxy。令v=vn…v2v1,y=ym…y2y1,其中vi,yj∈X,i=1,2,…,n,j=1,2,…,m。显然,当n=m时有v=y。若n uv=zxy⟹v=y⟹u=zx(因为uv=uyz) ⟹x≤u ⟹u=x(因为u,x∈A∪B且u是A∪B的极小元) ⟹uv=xy 所以,w=uv∈A∘C+B∘C。因此,(A+B)∘C⊆A∘C+B∘C。 例3给出一个在自然语言处理中被用到的右分配的强双幺半群,参见文献[12]。 例3:设X为字母表。令∧为X*上的二元运算。对任意的u,v∈X*,u∧v是u和v的最长公共后缀。在X*中额外添加一个字∞,要求w∧∞=∞∧w=w,w·∞=∞·w=∞对一切w∈X*∪{∞}都成立,其中·为字的并置。 例4:设X={a,b}且A={a},B={ba},C={ab}。易见,A,B,C∈S(X)。由于A+B=L(A∪B)={a}且A⊕B=U(A∪B)={ba},则有: C∘(A+B)={ab}∘{a}={aba} C∘(A⊕B)={ab}∘{ba}={abba} 又因为:C∘A+C∘B={aba}+{abba}={aba,abba} C∘A⊕C∘B={aba}⊕{abba}={aba,abba} 所以,C∘(A+B)≠C∘A+C∘B且C∘(A⊕B)≠C∘A⊕C∘B。 引理1:设X为非空集合, (K,+,·,0,1)∈LRS且α:X→K为映射。令乘法幺半群同态θ:X*→K是α的扩张。那么对任意的非空有限集A⊆X*,总有∑w∈Aθ(w)=∑w∈L(A)θ(w)。 证明:设u,v∈A,若u≤v,则v=xu,其中x∈X*。因为乘法同态θ是α的扩张,所以θ(ε)=1且θ(v)=θ(xu)=θ(x)θ(u)。由(K,+,·,0,1)∈LRS,知(K,+,·,0,1)满足恒等式x+xy≈x。故有: θ(u)+θ(v)=θ(u)+θ(u)θ(x)=θ(u) 所以有:∑w∈Aθ(w)=∑w∈A{v}θ(w)。进一步根据A的有限性得到 : ∑w∈Aθ(w)=∑w∈L(A)θ(w) 那么, 对任意的x∈X,有β(ι(x))=β({x})=θ(x)=α(x).因此,图1是交换的。 图1 α的扩张 下面证明β是同态映射。 β(A)+β(B) =∑w∈Aθ(w)+∑w∈Bθ(w) =∑w∈A∪Bθ(w)=∑w∈L(A∪B)θ(w) =∑w∈A+Bθ(w)=β(A+B), β(A)·β(B)=(∑w∈Aθ(w))·(∑w∈Bθ(w)) =∑u∈A,v∈Bθ(u)·θ(v) =∑w∈A∘Bθ(w)=β(A∘B) 这就证明了定理1和定理2 参考文献: [1]孙晓青,田径,李江华.具有拟稳定秩的环[J].西安理工大学学报, 2013,29(2): 188-191. Sun Xiaoqing, Tian Jing, Li Jianghua.Rings with quasi-stable range conditions[J].Journal of Xi’an University of Technology,2013,29 (2):188-191. [2]Bloom S, Ésik Z.Free shuffle algebras in language varieties[J].Theoretical Computer Science, 1996, 163:55-98. [3]Chatterjee K, Doyen L, Henzinger T.Quantitative languages[J].Lecture Notes in Computer Science, 2008, 5213:385-400. [5]Droste M, Stüber T, Vogler H.Weighted finite automata over strong bimonoids[J].Information Sciences, 2010, 180:156-166. [6]Chatterjee K, Doyen L, Henzinger T.Alternating weighted automata[J].Lecture Notes in Computer Science, 2009, 5699:3-13. [7]Chatterjee K, Doyen L, Henzinger T.Expressiveness and closure properties for quantitative languages: 24th LICS 2009[M].Los Angeles: IEEE Computer Society Press, 2009, 199-208. [8]Klir G J, Yuan B.Fuzzy sets and fuzzy logic, theory and application[M].New Jersey: Prentice-Hall PTR, 1995. [9]Burris S, Sankappanavar H P.A course in universal algebra[M].New York:Dover Publications, Incorporated, 2012. [10]Shyr H J.Lecture notes: free monoids and languages[M].3rd Edition.Taiwan:Hon Min Book Company, 2001. [11]Ito M, Jürgensen H,Shyr H J.Outfix and infix codes and related classes of languages[J].Journal of Computer and System Sciences, 1991, 43:484-508. [12]Mohri M.Minimization algorithms for sequential transducers[J].Theoretical Computer Science, 2000, 234:177-201.
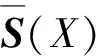
3 自由对象