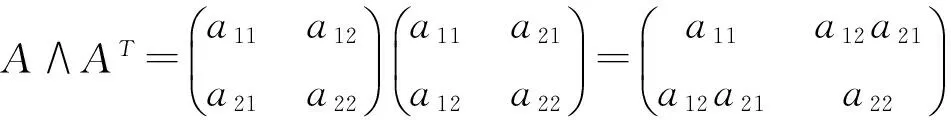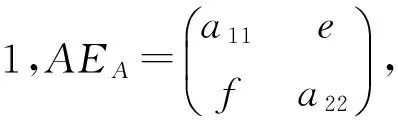祝祯祯,卢 涛

(淮北师范大学 数学科学学院,安徽 淮北 235000)

1 引言及预备知识

矩阵是现代数学中非常重要的概念，人们不仅关心数环与数域上的矩阵，还关心格上的矩阵．本文利用在有补的分配格L上定义的矩阵运算，给出了格上矩阵乘积的一些性质．约定(L，≤)为任意给定的至少有两个元素的有补的分配格，L的交，并运算分别记作∧和∨．L的最大元与最小元分别记作0和1．

定义1设(L，≤)是偏序集,如果对于任意的x,y∈L，{x,y}都有最小上界和最大下界,则称L关于偏序≤作成一个格．

由于最小上界和最大下界的唯一性,可以把求{x,y}的最小上界和最大下界看成x与y的二元运算∨和∧,即求x∨y和x∧y分别表示x与y的最小上界和最大下界．

这里要说明一点，本节中出现的∨和∧符号只代表格中的运算，而不再有其它的含义．

2 主要结果

记A*A=A2．

定义3若L是一个偏序集，当aij≤bij,aij,bij∈L，(i,j=1,2)时，称A≤B．

(1)E2=E；

(2)E*A=A*E；

(3)A*B*C=A*(B*C)．

证明略

定义4设A=(aij)∈L2×2，

(1)若A2≤A，则称A为传递矩阵;

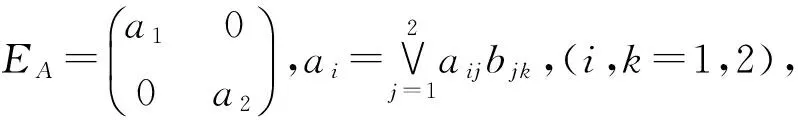
(3)若AT=A，则称A为对称矩阵;

(4)若A2=A，则称A为幂等矩阵；

(5)若对任意的A=(aij)，i,j=1,2,a11∨a22=1，则称A为对角补矩阵；

(6)若A2=0，则称A为幂零矩阵．

事实上，由文献[1]～[6]中定义容易验证以上的定义是合理的.

我们知道，对于一般的二阶矩阵A=(aij)，B=(bij),aij,bij∈R满足(AB)T=BTAT，而对于格上的矩阵却不一定成立，但当条件减弱便可得以下结论．

定理1对于任意的A∈L2×2，A*EA≤A，且(AEA)T=ATEA；而EAA≤AT，且(EAA)T=ATEA．

其中，记a12(a21∨a22)=e，a21(a11∨a12)=f．

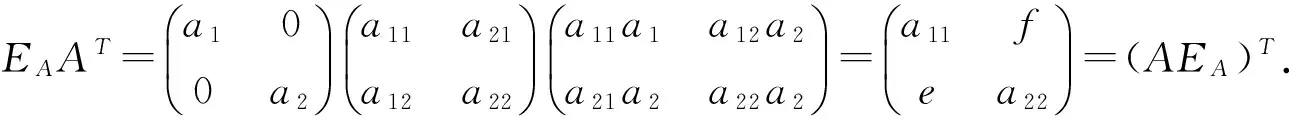
同理EAA≤AT，(EAA)T=ATEA．

在有补的偏序集L中，容易验证，对任意a,b∈L，a≠0,b∧b′=0,b∨b′=1,若a小于b，则a不小于b′．否则a小于b′，则a<(b∧b′)=0，矛盾．

定理2已知A为对角补矩阵，若A为自反矩阵，则a12a21=0．

证明由定义4(2)，a1=a11a11∨a12a21，a2=a22a22∨a12a21，由A是自反的，即a1≤a11,a2≤a22．所以a12a21≤a11，a12a21≤a22，由条件a11∨a22=1，故a12a21=0．

定理3若A为自反矩阵，则A是传递矩阵．

证明已知A为自反矩阵，a1=a11a11∨a12a21≤a11，a2=a22a22∨a12a21≤a22．由

a11a12∨a12a22=a12(a11∨a22)

定理4若A是传递的，则AT是传递的，并且B=A∧AT是传递的对称矩阵．

定理5若A为对角补矩阵且A为自反矩阵，则A为幂等矩阵．

由c1∨c2=1，记c1=1-c2，由A为幂等矩阵，易证A为对角补矩阵，即a11∨a22=1，记a11∨a22=1，从而

c1a11∨c2a22=[(1-c2)∩a11]∨[c2∩(1-a11)]=(a11-c2∨a11)∨(c2-c2∨a11)

=a11∩(c2-c2∨a11)-a22∩(c2-c2∨a11)=c2∨a11-c2∨a11-(c2∨a11-c2∨a11)=0

即(*)=0．所以ECA为幂等矩阵，得证．

定理6若A为幂等矩阵，则AEA,EAA，(EAA)T，(AEA)T都为幂等矩阵．

e=a12(a12∨a22)，f=a21(a11∨a12)，A为幂等矩阵，a12a21=0，ef=0，

e=e(a22∨a22),f=f(a11∨a22)，故(Δ)式=AEA．

同理，EAA也为幂等矩阵，又(EAA)T=ATEA，(AEA)T=EAAT，也易证(EAA)T，(AEA)T为幂等矩阵．

结论

由文献[8],我们知道二阶格矩阵对于计算机应用有很大的影响，然而基于格矩阵中的元素与其补元的和并不为零元，参考文献[7][9],以后将进一步研究反对称格矩阵以及一般格矩阵的广泛性质.

[1]王萼芳,石生明.高等代数[M].北京：高等教育出版社，1964.

[2]G.Gierz，Continuous Lattices and Domains[M].New York，Cambridge University Press，2003.

[3]胡先富,李 娜.格上传递矩阵的性质[J].四川师范大学学报(自然科学版)，2009,30(6):14～16．

[4]张 慧. 对幂等矩阵的研究[J].陕西科技大学学报(自然科学版)，2012,30(6):140～146.

[5]韩振芳，张 青.对称矩阵的一些性质和定理[J].河北北方学院学报(自然科学版)，2006,22(1):17～18.

[6] Abramsky S,JungA.Domain theory[M].New York:Oxford University Press,1994.

[7]张海山.反对称矩阵的若干性质[J].甘肃教育学院学报(自然科学版)，2003,17(3):15～18.

[8]张丽梅，赵建立等.用二值矩阵表示研究格矩阵的{1}-广义逆与{1，2}-广义逆[J].模糊系统与数学，2009,23(3):36～39.

[9]谭宜家.格矩阵的行列式与伴随矩阵[J].模糊系统与数学，2004, 18(2):168～171.