周 硕，韩明花，季本明

（东北电力大学 理学院，吉林 吉林132012）

0 引 言

矩阵及其特征值反问题在科学和工程计算中应用广泛［1－7］.矩阵的广义特征值反问题是根据给定的特征值及（或）特征向量的信息和附加条件，讨论Ax＝λBx成立的条件及通解表达式［2－5］.离散系统的扩充问题实际上是矩阵的扩充问题，矩阵扩充问题即为子矩阵约束下的矩阵反问题，因此研究矩阵扩充问题对矩阵理论及其实际应用具有重要意义［5－7］.广义反射阵P的自反阵与反自反阵在工程技术和科学计算等领域应用广泛［8－11］.文献［2］研究了广义反自反矩阵的广义特征值反问题；文献［3］研究了矩阵A，B分别为广义自反矩阵和广义反自反矩阵时的广义逆特征值问题；文献［5］利用矩阵对的广义奇异值分解研究了子矩阵约束下中心对称矩阵束的最佳逼近问题.本文利用矩阵对的商奇异值分解［12］方法，研究主子阵约束下广义自反矩阵的广义特征值反问题及其最佳逼近，并讨论了最佳逼近解的数值稳定性.

定义1 设P∈Cn×n，若P＝PH，P2＝In，则称P为广义反射阵.

定义2［8］设P∈Cm×m，Q∈Cn×n为广义反射阵，A∈Cm×n，若A＝PAQ，则称A 为关于矩阵对（P，Q）的广义自反矩阵.所有m×n阶关于矩阵对（P，Q）的广义自反矩阵全体记为（P，Q）；若A＝－PAQ，则称A为关于矩阵对（P，Q）的广义反自反矩阵.所有m×n阶关于矩阵对（P，Q）的广义反自反矩阵全体记为（P，Q）.

问题1 给定X＝（x1，x2，…，xk）∈Cn×k，Λ＝diag（λ1，λ2，…，λk）∈Ck×k和广义反射阵P∈Cm×m，Q∈Cn×n，A0，B0∈Cq×q，求矩阵A，B∈Cm×nr（P，Q），使得

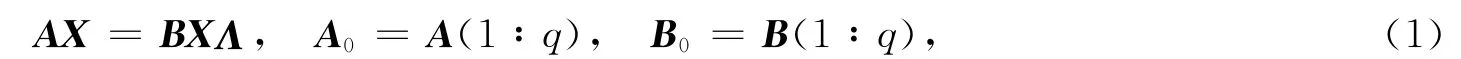
其中A（1∶q）和B（1∶q）分别是矩阵A和B的前q阶顺序主子阵.

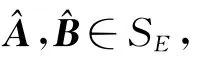
其中SE为问题1的解集.

当P，Q∈Rn×n为对称正交矩阵（即P＝PT＝P－1）时，问题1和问题2转化为主子阵约束下广义中心对称矩阵的广义特征值反问题；当P＝Q＝Sn时，问题1和问题2转化为主子阵约束下中心对称矩阵的广义特征值反问题［5］.

1 问题1的求解

引理1［8］设P∈Cm×m，Q∈Cn×n为广义反射矩阵，则存在一个m×m阶酉阵U和一个n×n阶酉阵V，使得P，Q的谱分解为

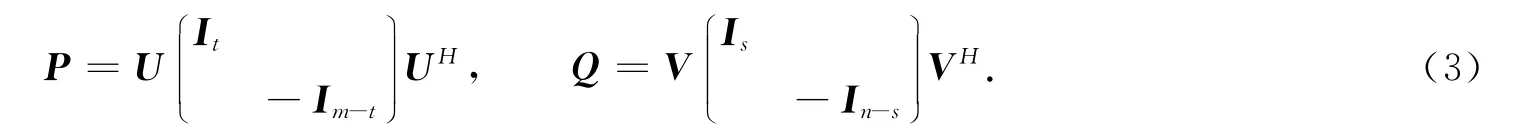
对文献［9］的相关结果进行推广，可得如下引理.

引理2 设A∈Cm×n，P∈Cm×m，Q∈Cn×n为广义反射矩阵，且P，Q 的谱分解为式（3），则A∈Cm×nr（P，Q）为广义自反阵当且仅当

引理3 对给定的X＝（x1，x2，…，xk）∈Cn×k，Λ＝diag（λ1，λ2，…，λk）∈Ck×k，矩阵方程AX＝BXΛ恒有解A，B∈Cm×n，且其解可表示为

其中：G∈Cm×（2n－r）是任意矩阵；U2∈C2n×（2n－r）是单位列酉阵，且

引理4 对给定的 X＝（x1，x2，…，xk）∈Cn×k，Λ＝diag（λ1，λ2，…，λk）∈Ck×k和广义反射阵P∈Cm×m，Q∈Cn×n，矩阵方程AX＝BXΛ恒有解A，B∈Cm×nr（P，Q），并且其解可表示为

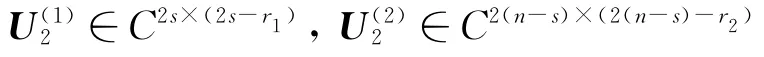
引理1给出了广义反射矩阵的谱分解形式，引理2～引理4是对文献［9］中相关结果的推广，给出了广义自反矩阵的结构、广义特征值反问题AX＝BXΛ有一般解及广义自反解的形式.

在引理4的基础上，可得AX＝BXΛ的广义自反解，再利用广义自反矩阵的结构及主子矩阵约束，可得问题1有解的充要条件及解的表达式.

记（Iq，0）U＝（D1，D2），其中：D1∈Cq×t；D2∈Cq×（m－t）.设D1，D2的商奇异值分解为

其中：E∈Cq×q为可逆矩阵；R∈Ct×t和F∈C（m－t）×（m－t）均为酉阵；

S＝diag（α1，α2，…，αs1）＞0；s1＝rank（D1）＋rank（D2）－l1；l1＝rank（D1，D2）；t1＝l1－rank（D2）；0，O1，O2为相应阶数的零矩阵.

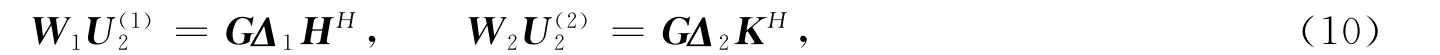
设

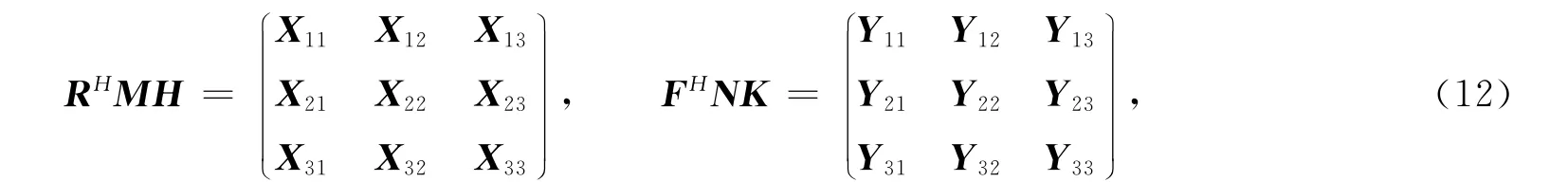
定理1 给定X＝（x1，x2，…，xk）∈Cn×k，Λ＝diag（λ1，λ2，…，λk）∈Ck×k和广义反射阵P∈Cm×m，Q∈Cn×n，A0，B0∈Cq×q，则问题1有解的充要条件是

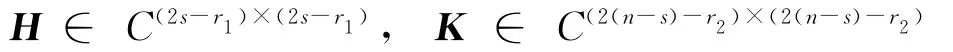
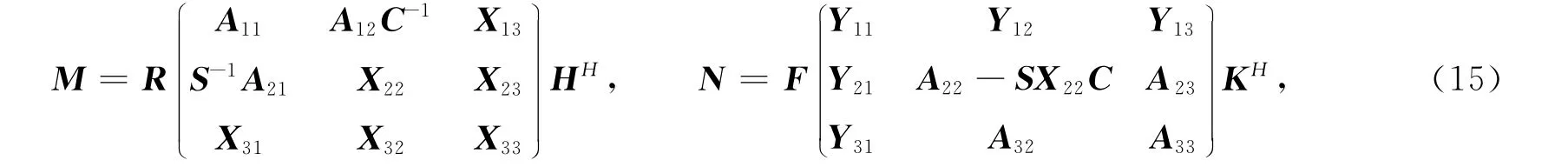
其中X31，X32，X33，X13，X23，X22，Y11，Y12，Y13，Y21，Y31为相应阶数的任意矩阵.

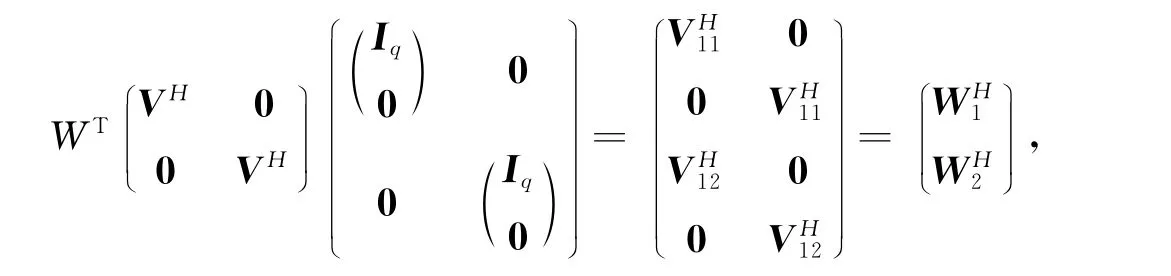
进而式（16）可转化为

即

将式（9）和式（11）～（13）代入式（19），可得

则式（17）成立当且仅当式（14）成立，同时可解得

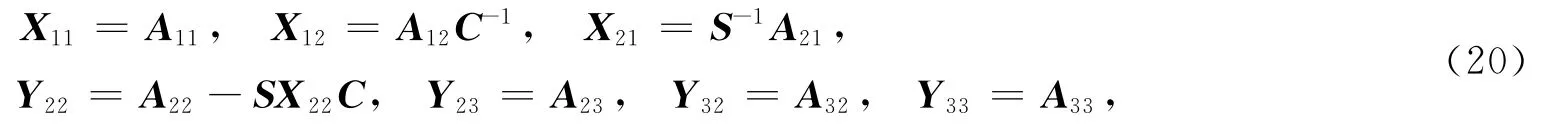
将式（20）代入式（12）可得式（15），故问题1解的一般形式为式（6）.

2 问题2的求解

证明：设

其中：G1＝（g1ij）；G2＝（g2ij）；E1＝（e1ij）；E2＝（e2ij）；F1＝（f1ij）；F2＝（f2ij）∈Rm×n.

令f（G）＝‖G－E‖2＋‖Λ1GΛ2－F‖2，则

由式（22）知f（G）＝min等价于

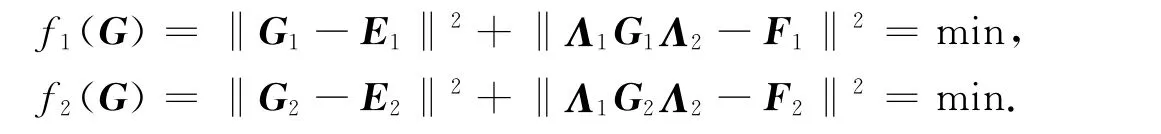
而

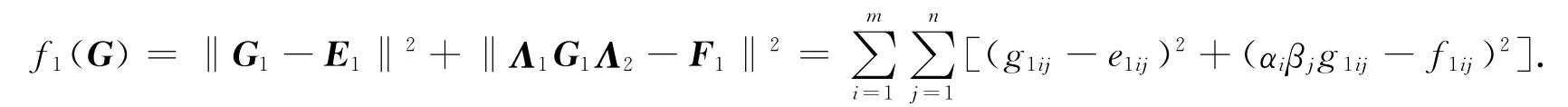
要使f1（G）最小，当且仅当

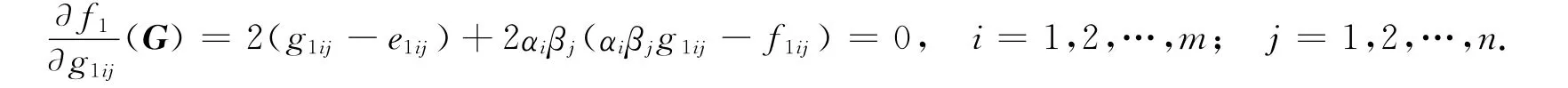
与式（12）的分块形式相同.

定理2 对给定的 X＝（x1，x2，…，xk）∈Cn×k，Λ＝diag（λ1，λ2，…，λk）∈Ck×k和广义反射阵P∈Cm×m，Q∈Cn×n，A＊，B＊∈Cm×n，问题1的解集由式（6）给出，则问题2有唯一最佳逼近解∈SE，可表示为

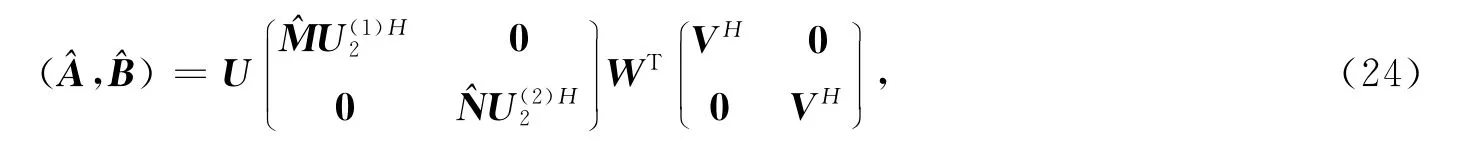
其中：

证明：由定理1及式（23），可得

故‖（A，B）－（A＊，B＊）‖＝min等价于

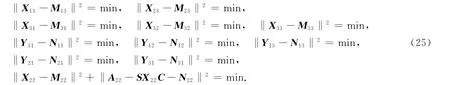
由式（25）及引理5可得问题2的解为式（24）.

3 最佳逼近解的稳定性

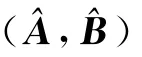
引理6 已 知 Δ＝ （xij）∈Cs1×s2，S＝diag（α1，α2，…，αs1），α1≥α2≥ … ≥αs1＞0，C＝diag（β1，β2，…，βs2），β1≥β2≥…≥βs2＞0，则

证明：由

可得式（26）成立.

引理7 已知ΔM22＝（mij）∈Cs1×s2，ΔN22＝（nij）∈Cs1×s2，Δ＝（xij）∈Cs1×s2，Φ＝（φij）∈≥βs2＞0，Δ＝Φ＊（ΔM22－S（ΔN22）C），则

证明：由

可得

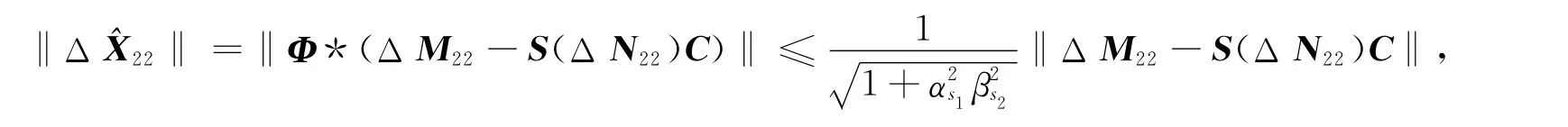
而

故由引理6和式（26），可得式（27）.

证明：由定理2及F范数的酉不变性，有

由引理6和引理7，得

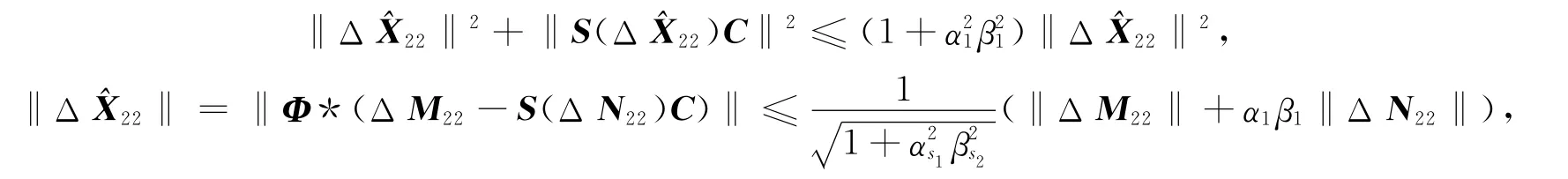
而

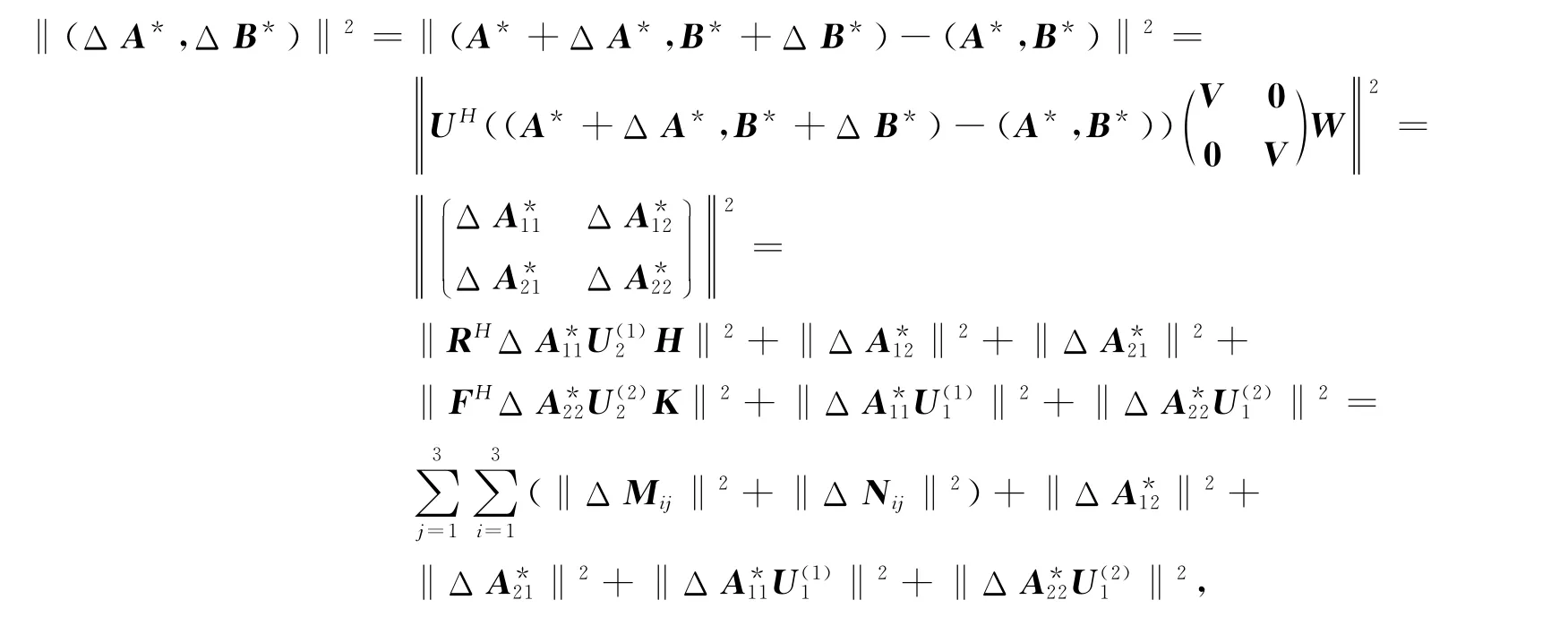
于是，由式（29）知

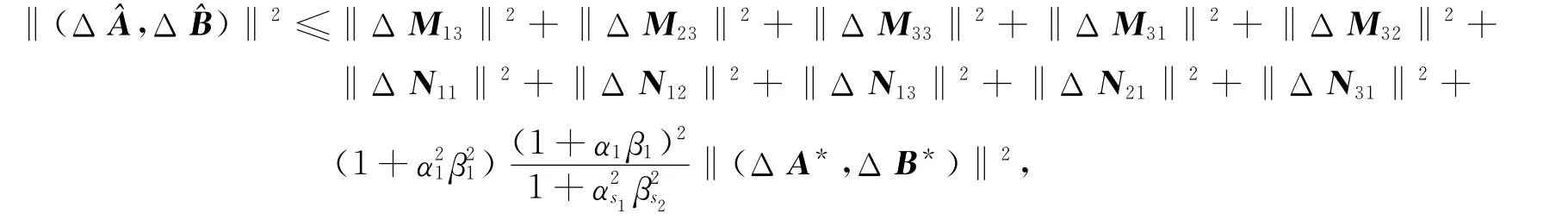
因此，公式（28）成立，证毕.

［1］周树荃，戴华.代数特征值反问题 ［M］.郑州：河南科学技术出版社，1991.

［2］DENG Ji－en， WANG Hai－ning，CUI Run－qing.Inverse Generalized Eigenvalue Problem for Generalized Antireflexive Matrices［J］.Journal of Henan Polytechnic University：Natural Science，2007，26（3）：340－344.（邓继恩，王海宁，崔润卿.广义反自反阵的广义特征值反问题 ［J］.河南理工大学学报：自然科学版，2007，26（3）：340－344.）

［3］LIU Neng－dong，ZHANG Zhong－zhi.Inverse Generalized Eigenvalue Problem for Generalized Reflexive and Generalized Anti－reflexive Matrices［J］.Journal of Natural Science of Hunan Normal University，2011，34（4）：1－6.（刘能东，张忠志.广义自反矩阵与广义反自反矩阵的广义逆特征值问题［J］.湖南师范大学自然科学学报，2011，34（4）：1－6.）

［4］WANG Jiang－tao，ZHANG Zhong－zhi，XIE Dong－xiu，et al.The Inverse Generalized Eigenvalue Problem and the Optimal Approximation for Hermitian－Reflexive Matrices ［J］.Journal on Numerical Methods and Computer Applications，2010，31（3）：232－240.（王江涛，张忠志，谢冬秀，等.埃尔米特自反矩阵的广义逆特征值问题与最佳逼近问题 ［J］.数值计算与计算机应用，2010，31（3）：232－240.）

［5］BAO Li－juan，DAI Hua.Optimal Approximation of Centrosymmetric Matrix Pencil with a Submatrix Pencil Constraint［J］.Chinese Journal of Engineering Mathematics，2013，30（2）：205－216.（鲍丽娟，戴华.子矩阵束约束下中心对称矩阵束的最佳逼近 ［J］.工程数学学报，2013，30（2）：205－216.）

［6］ZHAO Lin－lin，CHEN Guo－liang.One Kind of Inverse Eigenvalue Problems with a Submatrix Constraint［J］.Journal of East China Normal University：Natural Science，2010（5）：27－32.（赵琳琳，陈果良.子矩阵约束下的一类特征值反问题 ［J］.华东师范大学学报：自然科学版，2010（5）：27－32.）

［7］MO Rong－hua，LI Wen.The Inverse Eigenvalue Problem of Hermitian and Generalized Skew－Hamiltonian Matrices with a Submatrix Constraint and Its Approximation［J］.Acta Mathematica Scientia，2011，31A（3）：691－701.（莫荣华，黎稳.子矩阵约束下的埃尔米特广义反汉密尔顿矩阵特征值反问题及其最佳逼近 ［J］.数学物理学报，2011，31A（3）：691－701.）

［8］陈景良，陈向晖.特殊矩阵 ［M］.北京：清华大学出版社，2001：759－768.

［9］WU Chun－hong，LIN Lu.Inverse Generalized Eigenvalue Problem for Reflexive Matrices［J］.Journal of Xiamen University：Natural Science，2006，45（3）：305－310.（吴春红，林鹭.自反阵的广义特征值反问题 ［J］.厦门大学学报：自然科学版，2006，45（3）：305－310.）

［10］LONG Jian－hui，HU Xi－yan，ZHANG Lei.Least－Squares Solution for the Inverse Problem of Reflexive and Anti－reflexive Matrices ［J］.Chinese Journal of Engineering Mathematics，2004，21（8）：22－26.（龙 建 辉，胡锡炎，张磊.自反矩阵和反自反矩阵反问题的最小二乘解 ［J］.工程数学学报，2004，21（8）：22－26.）

［11］LIANG Mao－lin，DAI Li－fang，HE Wan－sheng.The Least－Squares Solutions for Two Kinds of Matrix Inverse Problems on Linear Manifolds［J］.Pure and Applied Mathematics，2011，27（6）：787－795.（梁茂林，代丽芳，何万生.线性流形上两类矩阵反问题的最小二乘解 ［J］.纯粹数学与应用数学，2011，27（6）：787－795.）

［12］CHU De－lin，Moor De B.On a Variational Formulation of the QSVD and the RSVD ［J］.Linear Algebra and Its Applications，2000，311：61－78.